DOCSLIB.ORG

Statistical Process Control Prof

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Statistical Process Control Prof Statistical Process Control Prof. Robert Leachman IEOR 130 Fall, 2020 Introduction • Quality control is about controlling manufacturing or service operations such that the output of those operations conforms to specifications of acceptable quality. • Statistical process control (SPC), also known as statistical quality control (SQC), dates back to the early 1930s and is primarily the invention of one man. The chief developer was Walter Shewhart, a scientist employed by Bell Telephone Laboratories. • Control charts (discussed below) are sometimes termed Shewhart Control Charts in recognition of his contributions. Introduction (cont.) • W. Edwards Deming, the man credited with exporting statistical quality control methodology to the Japanese and popularizing it, was an assistant to Shewhart. • Deming stressed in his teachings that understanding the statistical variation of manufacturing processes is a precursor to designing an effective quality control system. That is, one needs to quantitatively characterize process variation in order to know how to produce products that conform to specifications. Introduction (cont.) • Briefly, a control chart is a graphical method for detecting if the underlying distribution of variation of some measurable characteristic of the product seems to have undergone a shift. Such a shift likely reflects a subtle drift or change to the desired manufacturing process that needs to be corrected in order to maintain good quality output. • Control charts are very practical and easy to use, yet they are grounded in rigorous statistical theory. In short, they are a fine example of excellent industrial engineering. History • Despite their great value, initial use of control charts in the late 1930s and early 1940s was mostly confined to Western Electric factories making telephony equipment. (Western Electric was a manufacturing subsidiary of AT&T.) Evidently, the notion of using formal statistics to manage manufacturing was too much to accept for many American manufacturing managers at the time. • Following World War II, Japanese industry was decimated and in urgent need of rebuilding. It may be hard to imagine today, but in the 1950s, Japanese products had a low-quality reputation in America. • W. Edwards Deming went to Japan in the 1950s, and his SPC teachings were quickly embraced by Japanese management. History (cont.) • Through the 1960s, 1970s and 1980s, many Japanese-made products were improved dramatically and eventually surpassed competing American- made products in terms of quality, cost and consumer favor. • Many American industries lost substantial domestic market share or were driven completely out of business. • This led to a “quality revolution” in US industries during the 1980s and 1990s featuring widespread implementation and acceptance of SPC and other quality management initiatives. Important additions were made to quality control theory and practice, especially Motorola’s Six Sigma controllability methodology (to be discussed). • It is ironic that a brilliant American invention was not accepted by American industries until threatened by Japanese competition making good use of that invention. Control Charts • Control charts provide a simple graphical means of monitoring a process in real time. Today, they have gained wide acceptance in industry – you would be hard-pressed to find a volume manufacturing plant producing technologically advanced products anywhere in the world that is not using SPC extensively. • A control chart maps the output of a production process over time and signals when a change in the probability distribution generating observations seems to have occurred. To construct a control chart one uses information about the probability distribution of process variation and fundamental results from probability theory. Central Limit Theorem • Most types of control charts are based on the Central Limit Theorem of statistics. Roughly speaking, the central limit theorem says that the distribution of a sum of independent and identically distributed (IID) random variables approaches the normal distribution as the number of terms in the sum increases. • Generally, the distribution of the sum converges very quickly to a normal distribution. For example, consider a random variable with a uniform distribution on the interval (0, 1). See Figure 1. Figure 1 Probability density of a uniform variate on (0, 1) Central Limit Theorem • Now assume the three random variables X1, X2, and X3 are independent, each of which has the uniform distribution on the interval (0, 1). Consider the random variable W = X1 + X2 + X3. If one plots the distribution of W, it tracks remarkably close to a normal distribution with the same mean and variance. See Figure 2. If we were to continue to add independent random variables, the agreement would be even closer. Figure 2 Density of the sum of three uniform random variables Central Limit Theorem (cont.) • If (X1, X2, … , Xn) is a random sample, the sample mean is defined as 1 n X = ∑ X i . n i=1 • The Central Limit Theorem tells us that, regardless of the distribution of Xi, the sample mean will have a normal distribution, provided the variables are IID. • Suppose that a random variable Z has the standard normal distribution (i.e., mean 0 and variance 1). Then, according to the table of the unit normal distribution (see Table A-1 in the SPC notes), P{− 3 ≤ Z ≤ 3}= 0.9974. Central Limit Theorem (cont.) • In other words, the likelihood of obtaining a value of Z either larger than 3 or less than -3 is 0.0026, or roughly 3 chances in 1,000. If such a value of Z is encountered, it is more likely that the IID assumption has been violated, i.e., there has been a drift or shift of the process that needs to be corrected. • This is the basis of the so-called three-sigma limits that have become the de facto standard in SPC. Back to Control Charts • Consider the average of n samples of a process variable. The Central Limit Theorem tells us it should be (approximately) normally distributed. Suppose the mean of each� sample is µ and the standard deviation is σ. The mean of is expressed as 1 n 1 n 1 n 1 n 1 �EX = E ∑ X i = E∑ X i = ∑ EX i = ∑ µ = (n)µ = µ. n i=1 n i=1 n i=1 n i=1 n • The variance of is derived as follows: 1 n 1 n �= = Var X Var ∑ X i 2 Var ∑ X i . n i=1 n i=1 • Now n 2 Var∑ X i = n Var(X i ) = nσ , i=1 Control Charts (cont.) • Therefore, = . 2 • Hence the standard deviation of is� σ � . n • Therefore, the standardized variate X − µ Z = σ n has (approximately) the normal distribution with mean zero and unit variance. Control Charts (cont.) • It follows that X − µ P − 3 ≤ ≤ 3 = 0.9974, σ n or equivalently, 3σ 3σ Pµ − ≤ X ≤ µ + = 0.9974. n n • That is, the likelihood of observing a value of either larger than + or 3 less than is 0.0026. Such an event is sufficiently� rare that if it were to occur, it is more3 likely to have been caused by a shift in the population mean µ, than to have− been the result of chance. • This is the basis of the theory of control charts. Control Charts (cont.) • A manufacturing process is said to be in statistical control if a stable system of chance causes is operating. That is, the underlying probability distribution generating observations of the process variable is not changing with time. • When the observed value of the sample mean of a group of observations falls outside the appropriate three-sigma limits, it is likely that there has been a change in the probability distribution generating observations. When an observed value falls outside these limits, it is customary to say the process is out-of-control, i.e., it is out of statistical control. Control Charts for Continuous Variables • For a continuous variable describing the quality of the process, control charts may be set up to track both the mean of the variable over fixed-size samples (the -chart) and its range (maximum minus minimum) over fixed- size samples (the R-chart). � • An out-of-control signal on the -chart indicates that the process mean has shifted; an out-of-control signal on the R-chart indicates that the process variance has changed. Either out�-of-control signal should trigger a halt of the process. • There should be an investigation to ascertain if and why the process is no longer in statistical control. (An alternative explanation is that the observations were not measured correctly.) • The investigation culminates in corrective action to restore the process to statistical control, whereupon manufacturing is resumed. In this way, quality losses can be kept to a minimum. and Charts • An -chart requires that collection of data on the process variable be �broken down into subgroups of fixed size. The most common size of subgroups� in industrial practice is n = 5. The subgroup size n ought to be at least four in order to have an accurate application of the Central Limit Theorem. • To construct an -chart, it is necessary to estimate the sample mean and the sample variance of the process variable. This could be done using standard statistical� estimates from an initial population of N measurements (ideally, N much larger than n) of the variable: 1 1 = , = . 1 2 2 � � � − � =1 − =1 and Charts • However, it is not recommended that one use the sample standard �deviation s as an estimator of σ when constructing an -chart. For s to be an accurate estimator of σ, it is necessary that the underlying mean of the sample population be constant. Because the� purpose of an -chart is to determine whether a shift in the mean has occurred, we should not assume a priori that the mean is constant when estimating� σ.
Load more

Recommended publications
  • Methods and Philosophy of Statistical Process Control
    5Methods and Philosophy of Statistical Process Control CHAPTER OUTLINE 5.1 INTRODUCTION 5.4 THE REST OF THE MAGNIFICENT 5.2 CHANCE AND ASSIGNABLE CAUSES SEVEN OF QUALITY VARIATION 5.5 IMPLEMENTING SPC IN A 5.3 STATISTICAL BASIS OF THE CONTROL QUALITY IMPROVEMENT CHART PROGRAM 5.3.1 Basic Principles 5.6 AN APPLICATION OF SPC 5.3.2 Choice of Control Limits 5.7 APPLICATIONS OF STATISTICAL PROCESS CONTROL AND QUALITY 5.3.3 Sample Size and Sampling IMPROVEMENT TOOLS IN Frequency TRANSACTIONAL AND SERVICE 5.3.4 Rational Subgroups BUSINESSES 5.3.5 Analysis of Patterns on Control Charts Supplemental Material for Chapter 5 5.3.6 Discussion of Sensitizing S5.1 A SIMPLE ALTERNATIVE TO RUNS Rules for Control Charts RULES ON THEx CHART 5.3.7 Phase I and Phase II Control Chart Application The supplemental material is on the textbook Website www.wiley.com/college/montgomery. CHAPTER OVERVIEW AND LEARNING OBJECTIVES This chapter has three objectives. The first is to present the basic statistical control process (SPC) problem-solving tools, called the magnificent seven, and to illustrate how these tools form a cohesive, practical framework for quality improvement. These tools form an impor- tant basic approach to both reducing variability and monitoring the performance of a process, and are widely used in both the analyze and control steps of DMAIC. The second objective is to describe the statistical basis of the Shewhart control chart. The reader will see how decisions 179 180 Chapter 5 ■ Methods and Philosophy of Statistical Process Control about sample size, sampling interval, and placement of control limits affect the performance of a control chart.
    [Show full text]
  • D Quality and Reliability Engineering 4 0 0 4 4 3 70 30 20 0
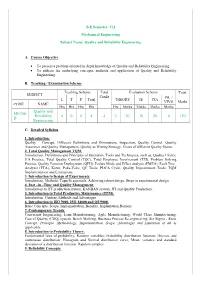
    B.E Semester: VII Mechanical Engineering Subject Name: Quality and Reliability Engineering A. Course Objective To present a problem oriented in depth knowledge of Quality and Reliability Engineering. To address the underlying concepts, methods and application of Quality and Reliability Engineering. B. Teaching / Examination Scheme Teaching Scheme Total Evaluation Scheme Total SUBJECT Credit PR. / L T P Total THEORY IE CIA VIVO Marks CODE NAME Hrs Hrs Hrs Hrs Hrs Marks Marks Marks Marks Quality and ME706- Reliability 4 0 0 4 4 3 70 30 20 0 120 D Engineering C. Detailed Syllabus 1. Introduction: Quality – Concept, Different Definitions and Dimensions, Inspection, Quality Control, Quality Assurance and Quality Management, Quality as Wining Strategy, Views of different Quality Gurus. 2. Total Quality Management TQM: Introduction, Definitions and Principles of Operation, Tools and Techniques, such as, Quality Circles, 5 S Practice, Total Quality Control (TQC), Total Employee Involvement (TEI), Problem Solving Process, Quality Function Deployment (QFD), Failure Mode and Effect analysis (FMEA), Fault Tree Analysis (FTA), Kizen, Poka-Yoke, QC Tools, PDCA Cycle, Quality Improvement Tools, TQM Implementation and Limitations. 3. Introduction to Design of Experiments: Introduction, Methods, Taguchi approach, Achieving robust design, Steps in experimental design 4. Just –in –Time and Quality Management: Introduction to JIT production system, KANBAN system, JIT and Quality Production. 5. Introduction to Total Productive Maintenance (TPM): Introduction, Content, Methods and Advantages 6. Introduction to ISO 9000, ISO 14000 and QS 9000: Basic Concepts, Scope, Implementation, Benefits, Implantation Barriers 7. Contemporary Trends: Concurrent Engineering, Lean Manufacturing, Agile Manufacturing, World Class Manufacturing, Cost of Quality (COQ) system, Bench Marking, Business Process Re-engineering, Six Sigma - Basic Concept, Principle, Methodology, Implementation, Scope, Advantages and Limitation of all as applicable.
    [Show full text]
  • Quality Assurance: Best Practices in Clinical SAS® Programming
    NESUG 2012 Management, Administration and Support Quality Assurance: Best Practices in Clinical SAS® Programming Parag Shiralkar eClinical Solutions, a Division of Eliassen Group Abstract SAS® programmers working on clinical reporting projects are often under constant pressure of meeting tight timelines, producing best quality SAS® code and of meeting needs of customers. As per regulatory guidelines, a typical clinical report or dataset generation using SAS® software is considered as software development. Moreover, since statistical reporting and clinical programming is a part of clinical trial processes, such processes are required to follow strict quality assurance guidelines. While SAS® programmers completely focus on getting best quality deliverable out in a timely manner, quality assurance needs often get lesser priorities or may get unclearly understood by clinical SAS® programming staff. Most of the quality assurance practices are often focused on ‘process adherence’. Statistical programmers using SAS® software and working on clinical reporting tasks need to maintain adequate documentation for the processes they follow. Quality control strategy should be planned prevalently before starting any programming work. Adherence to standard operating procedures, maintenance of necessary audit trails, and necessary and sufficient documentation are key aspects of quality. This paper elaborates on best quality assurance practices which statistical programmers working in pharmaceutical industry are recommended to follow. These quality practices
    [Show full text]
  • Statistical Process Control for Monitoring Nonlinear Profiles: a Six Sigma Project on Curing Process
    This is the author’s final, peer-reviewed manuscript as accepted for publication. The publisher-formatted version may be available through the publisher’s web site or your institution’s library. Statistical process control for monitoring nonlinear profiles: a six sigma project on curing process Shing I. Chang, Tzong-Ru Tsai, Dennis K. J. Lin, Shih-Hsiung Chou, & Yu-Siang Lin How to cite this manuscript If you make reference to this version of the manuscript, use the following information: Chang, S. I., Tsai, T., Lin, D. K. J., Chou, S., & Lin, Y. (2012). Statistical process control for monitoring nonlinear profiles: A six sigma project on curing process. Retrieved from http://krex.ksu.edu Published Version Information Citation: Chang, S. I., Tsai, T., Lin, D. K. J., Chou, S., & Lin, Y. (2012). Statistical process control for monitoring nonlinear profiles: A six sigma project on curing process. Quality Engineering, 24(2), 251-263. Copyright: Copyright © Taylor & Francis Group, LLC. Digital Object Identifier (DOI): doi:10.1080/08982112.2012.641149 Publisher’s Link: http://www.tandfonline.com/doi/abs/10.1080/08982112.2012.641149 This item was retrieved from the K-State Research Exchange (K-REx), the institutional repository of Kansas State University. K-REx is available at http://krex.ksu.edu Statistical Process Control for Monitoring Nonlinear Profiles: A Six Sigma Project on Curing Process Shing I Chang1, Tzong‐Ru Tsai2, Dennis K.J. Lin3, Shih‐Hsiung Chou1 & Yu‐Siang Lin4 1Quality Engineering Laboratory, Department of Industrial and Manufacturing Systems Engineering, Kansas State University, USA 2Department of Statistics, Tamkang University, Danshui District, New Taipei City 25137 Taiwan 3Department of Statistics, Pennsylvania State University, USA 4Department of Industrial Management, National Taiwan University of Science and Technology, Taipei, Taiwan ABSTRACT Curing duration and target temperature are the most critical process parameters for high- pressure hose products.
    [Show full text]
  • Data Quality Monitoring and Surveillance System Evaluation
    TECHNICAL DOCUMENT Data quality monitoring and surveillance system evaluation A handbook of methods and applications www.ecdc.europa.eu ECDC TECHNICAL DOCUMENT Data quality monitoring and surveillance system evaluation A handbook of methods and applications This publication of the European Centre for Disease Prevention and Control (ECDC) was coordinated by Isabelle Devaux (senior expert, Epidemiological Methods, ECDC). Contributing authors John Brazil (Health Protection Surveillance Centre, Ireland; Section 2.4), Bruno Ciancio (ECDC; Chapter 1, Section 2.1), Isabelle Devaux (ECDC; Chapter 1, Sections 3.1 and 3.2), James Freed (Public Health England, United Kingdom; Sections 2.1 and 3.2), Magid Herida (Institut for Public Health Surveillance, France; Section 3.8 ), Jana Kerlik (Public Health Authority of the Slovak Republic; Section 2.1), Scott McNabb (Emory University, United States of America; Sections 2.1 and 3.8), Kassiani Mellou (Hellenic Centre for Disease Control and Prevention, Greece; Sections 2.2, 2.3, 3.3, 3.4 and 3.5), Gerardo Priotto (World Health Organization; Section 3.6), Simone van der Plas (National Institute of Public Health and the Environment, the Netherlands; Chapter 4), Bart van der Zanden (Public Health Agency of Sweden; Chapter 4), Edward Valesco (Robert Koch Institute, Germany; Sections 3.1 and 3.2). Project working group members: Maria Avdicova (Public Health Authority of the Slovak Republic), Sandro Bonfigli (National Institute of Health, Italy), Mike Catchpole (Public Health England, United Kingdom), Agnes
    [Show full text]
  • Quality Control and Reliability Engineering 1152Au128 3 0 0 3
    L T P C QUALITY CONTROL AND RELIABILITY ENGINEERING 1152AU128 3 0 0 3 1. Preamble This course provides the essentiality of SQC, sampling and reliability engineering. Study on various types of control charts, six sigma and process capability to help the students understand various quality control techniques. Reliability engineering focuses on the dependability, failure mode analysis, reliability prediction and management of a system 2. Pre-requisite NIL 3. Course Outcomes Upon the successful completion of the course, learners will be able to Level of learning CO Course Outcomes domain (Based on Nos. C01 Explain the basic concepts in Statistical Process Control K2 Apply statistical sampling to determine whether to accept or C02 K2 reject a production lot Predict lifecycle management of a product by applying C03 K2 reliability engineering techniques. C04 Analyze data to determine the cause of a failure K2 Estimate the reliability of a component by applying RDB, C05 K2 FMEA and Fault tree analysis. 4. Correlation with Programme Outcomes Cos PO1 PO2 PO3 PO4 PO5 PO6 PO7 PO8 PO9 PO10 PO11 PO12 PSO1 PSO2 CO1 H H H M L H M L CO2 H H H M L H H M CO3 H H H M L H L H CO4 H H H M L H M M CO5 H H H M L H L H H- High; M-Medium; L-Low 5. Course content UNIT I STATISTICAL QUALITY CONTROL L-9 Methods and Philosophy of Statistical Process Control - Control Charts for Variables and Attributes Cumulative Sum and Exponentially Weighted Moving Average Control Charts - Other SPC Techniques Process - Capability Analysis - Six Sigma Concept.
    [Show full text]
  • Achieving Total Quality Management in Construction Project Using Six Sigma Concept
    International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 05 Issue: 06 | June 2018 www.irjet.net p-ISSN: 2395-0072 Achieving Total Quality Management in Construction Project Using Six Sigma Concept Dr.Divakar.K1 and Nishaant.Ha2 1Associate Professor in Civil Engineering, Coimbatore Institute of Technology, Coimbatore-641014 2Assistant Professor in Civil Engineering, Kumaraguru College of Technology, Coimbatore-641049 ---------------------------------------------------------------------***--------------------------------------------------------------------- Abstract - A Six Sigma approach is one of the most Low Sui Pheng and Mok Sze Hui (2004) examined the efficient quality improvement processes. In this study, six strategies and concepts of Six Sigma and implemented sigma concepts were applied in construction scheduling those concepts in construction industry. A. D. Lade et.al. process to avoid delay as well as to maintain the quality of (2015) analysed the quality performance of Ready Mix the construction activities. Detailed schedule of the building Concrete (RMC) plant at Mumbai, India, using the six was analysed & also the updated schedule was verified. At sigma philosophy had been evaluated using various this stage, DMAIC (Define, Measure, Analyse, Improve and quality tools and sigma value was calculated. According to Control) principle was implemented. The variation in the the sigma level, recommendations were given for the scheduling due to delay of the activities was noted down. improvement. Seung Heon Han et.al. in their study they Delay reasons and their impacts in the whole project were developed a general methodology to apply the six sigma calculated. All delayed activities were considered as principles on construction operations rather than “Defects”. DPMO (Defects Per Million Opportunities) was construction materials in terms of the barometers to calculated.
    [Show full text]
  • The Use of Six Sigma in Healthcare
    The Use of Six Sigma in Healthcare Jayanta K. Bandyopadhyay And Karen Coppens Central Michigan University Mt. Pleasant, Michigan, U.S.A. International Journal of Quality & Productivity Management Bandyopadhyay and Volume 5, No. 1 December 15, 2005 Coppens Six Sigma Approach to Healthcare Quality and Productivity Management By Jayanta K. Bandyopadhyay and Karen Coppens Central Michigan University Abstract: For decades the U.S. health care industry has been operating on its own way ignoring emerging factors such as competition, patient safety, skyrocketing health care cost, liability, malpractice insurance cost and use of DRG for Medicare and insurance payment. However, as these factors became more prevalent and competition within the industry intensified, many U.S. hospitals have been becoming increasingly aware of the critical needs of controlling the operating costs and meet and even exceeds the expectations of patient care quality. This paper presents a model of Six Sigma approach to health care quality management for hospitals in the U.S. and abroad. Keywords: six sigma, quality and productivity management in healthcare Introduction The health care industry in the U.S has been operating on its own traditional economic domain ignoring current emerging factors such as competition, patient safety, skyrocketing health care cost, liability from malpractice lawsuits and more government control on Medicare payment.( Hansson, 2000). But in recent years, these factors have become more prevalent and competition within the industry has been intensified, and many U.S. hospitals has been becoming increasingly aware of the critical needs of controlling their operating costs and meet the expectations of patient care quality (Chow-Chua et.al,2000).
    [Show full text]
  • Statistical Quality Control Methods in Infection Control and Hospital Epidemiology, Part I: Introduction and Basic Theory Author(S): James C
    Statistical Quality Control Methods in Infection Control and Hospital Epidemiology, Part I: Introduction and Basic Theory Author(s): James C. Benneyan Source: Infection Control and Hospital Epidemiology, Vol. 19, No. 3 (Mar., 1998), pp. 194-214 Published by: The University of Chicago Press Stable URL: http://www.jstor.org/stable/30143442 Accessed: 25/06/2010 18:26 Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/page/info/about/policies/terms.jsp. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/action/showPublisher?publisherCode=ucpress. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. The University of Chicago Press is collaborating with JSTOR to digitize, preserve and extend access to Infection Control and Hospital Epidemiology.
    [Show full text]
  • 4. Six Sigma Six Sigma Is a Set of Strategies, Techniques, and Tools For
    4. Six Sigma Six Sigma is a set of strategies, techniques, and tools for process improvement. It was developed by Motorola in 1986. Six Sigma became famous when Jack Welch made it central to his successful business strategy at General Electric in 1995. Today, it is used in many industrial sectors. Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects (errors) and minimizing variability in manufacturing and business processes.[5] It uses a set of quality management methods, including statistical methods, and creates a special infrastructure of people within the organization ("Champions", "Black Belts", "Green Belts", "Yellow Belts", etc.) who are experts in the methods. Each Six Sigma project carried out within an organization follows a defined sequence of steps and has quantified value targets, for example: reduce process cycle time, reduce pollution, reduce costs, increase customer satisfaction, and increase profits. The term Six Sigma originated from terminology associated with manufacturing, specifically terms associated with statistical modeling of manufacturing processes. The maturity of a manufacturing process can be described by a sigma rating indicating its yield or the percentage of defect-free products it creates. A six sigma process is one in which 99.9999998% of the products manufactured are statistically expected to be free of defects (0.002 defective parts/million), although, as discussed below, this defect level corresponds to only a 4.5 sigma level. Motorola set a goal of "six sigma" for all of its manufacturing operations, and this goal became a by-word for the management and engineering practices used to achieve it.
    [Show full text]
  • Developing an Innovative and Creative Hands-On Lean Six Sigma Manufacturing Experiments for Engineering Education
    Engineering, Technology & Applied Science Research Vol. 6, No. 6, 2016, 1297-1302 1297 Developing an Innovative and Creative Hands-on Lean Six Sigma Manufacturing Experiments for Engineering Education Isam Elbadawi Mohamed Aichouni Noor Aite Messaoudene Industrial Engineering Industrial Engineering Mechanical Engineering University of Hail University of Hail University of Hail Hail, Saudi Arabia Hail, Saudi Arabia Hail, Saudi Arabia [email protected], [email protected] [email protected] [email protected] Abstract—The goal of this study was to develop an innovative relevant to the needs of both students and market place. Such and creative hands-on project based on Lean Six Sigma integration is particularly important not only because the world experiments for engineering education at the College of has changed tremendously and new challenges have surfaced Engineering at the University of Hail. The exercises were over the last decade, but also because a considerable number of designed using junction box assembly to meet the following the students who join engineering schools have probably never learning outcomes: 1-to provide students with solid experience on had their hands on any practical engineering project. At the waste elimination and variation reduction and 2-to engage present, this integration has become an essential practice in students in exercises related to assembly line mass production most engineering schools worldwide. However, the number and motion study. To achieve these objectives, students were and complexity of the project-based courses significantly vary introduced to the principles of Lean manufacturing and Six among institutions with some having a project-based Sigma through various pedagogical activities such as classroom component to almost every engineering course [1] and others instruction, laboratory experiments, hands-on exercises, and that have only a few of such projects.
    [Show full text]
  • Success of Manufacturing Industries – Role of Six Sigma
    MATEC Web of Conferences 144, 05002 (2018) https://doi.org/10.1051/matecconf/201814405002 RiMES 2017 Success of manufacturing industries – Role of Six Sigma N. Venkatesh1* and C. Sumangala2 1Department of Mechanical Engineering, Canara College of Engineering, Benjanapadavu, Bantwal 574 219, Karnataka, India 2Department of MBA, University of Mysore, Mysore 570005, Karnataka, India Abstract. Six Sigma is a phenomenal quality management concepts which has helped many organizations to overcome quality crisis in the recent past. Six Sigma is observed as a very promising quality management tool for any organization to make its presence felt in the corporate world as it emphasizes on obtaining a fruitful solution to improve accuracy, reduce defect thereby reduce the cost and improve profits. The main objective of this investigation is to unearth the extent to which the companies have been benefitted due to Six Sigma implementation. This article presents the results based on the analysis of collective opinion of employees of various Indian manufacturing industries that have implemented Six Sigma. This research also examines interrelationship among various parameters defined in the research. The research revealed that industries are benefitted irrespective of their nature in terms of their growth, financial benefits, productivity and satisfaction of the customer. However, peoples’ equity that deals with the benefits that employees obtain after Six Sigma implementation is not certain. The research also revealed the existence of strong interrelationship among various parameters used to measure the success of Six Sigma. Keywords: Six Sigma; Qualitative analysis; manufacturing industry. 1 Introduction The Six Sigma philosophy aims to maintain a process within control limits in order to record no defects (Arendt, 2008).
    [Show full text]