DOCSLIB.ORG

Quantum Phase Transition and Ferromagnetism in Co 1+X Sn

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Quantum Phase Transition and Ferromagnetism in Co 1+X Sn University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Faculty Publications from Nebraska Center for Materials and Nanoscience, Nebraska Center Materials and Nanoscience for (NCMN) 2019 Quantum phase transition and ferromagnetism in Co1+xSn Rabindra Pahari Balamurugan Balasubramanian Rohit Pathak Manh Coung Nguyen Shah R. Valloppilly See next page for additional authors Follow this and additional works at: https://digitalcommons.unl.edu/cmrafacpub Part of the Atomic, Molecular and Optical Physics Commons, Condensed Matter Physics Commons, Engineering Physics Commons, and the Other Physics Commons This Article is brought to you for free and open access by the Materials and Nanoscience, Nebraska Center for (NCMN) at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Faculty Publications from Nebraska Center for Materials and Nanoscience by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Authors Rabindra Pahari, Balamurugan Balasubramanian, Rohit Pathak, Manh Coung Nguyen, Shah R. Valloppilly, Ralph Skomski, Arti Kashyap, Cai-Zhuang Wang, Kai-Ming Ho, George C. Hadjipanayis, and David J. Sellmyer PHYSICAL REVIEW B 99, 184438 (2019) Quantum phase transition and ferromagnetism in Co1+xSn Rabindra Pahari,1,2 Balamurugan Balasubramanian,1,2,* Rohit Pathak,3 Manh Cuong Nguyen,4,5 Shah R. Valloppilly,1 Ralph Skomski,1,2 Arti Kashyap,3 Cai-Zhuang Wang,4,5 Kai-Ming Ho,4,5 George C. Hadjipanayis,6 and David J. Sellmyer1,2,† 1Nebraska Center for Materials and Nanoscience, University of Nebraska, Lincoln, Nebraska 68588, USA 2Department of Physics and Astronomy, University of Nebraska, Lincoln, Nebraska 68588, USA 3School of Basic Sciences, IIT Mandi, Mandi, Himachal Pradesh 175005, India 4Ames Laboratory, US Department of Energy, Ames, Iowa 50011, USA 5Department of Physics and Astronomy, Iowa State University, Ames, Iowa 50011, USA 6Department of Physics and Astronomy, University of Delaware, Newark, Delaware 19716, USA (Received 22 April 2019; revised manuscript received 9 May 2019; published 28 May 2019) The onset of ferromagnetism in cobalt-tin alloys is investigated experimentally and theoretically. The Co1+xSn alloys were prepared by rapid quenching from the melt and form a modified hexagonal NiAs-type crystal structure for 0.45 x 1. The magnetic behavior is described analytically and by density-functional theory using supercells and the coherent-potential approximation. The excess of Co concentration x, which enters the interstitial 2d sites in the hypothetical NiAs-ordered parent alloy CoSn, yields a Griffiths-like phase and, above a quantum critical point (xc ≈ 0.65), a quantum phase transition to ferromagnetic order. Quantum critical exponents are determined on the paramagnetic and ferromagnetic sides of the transition and related to the nature of the magnetism in itinerant systems with different types of chemical disorder. DOI: 10.1103/PhysRevB.99.184438 I. INTRODUCTION desirable magnetic properties. The Co1+xSn system is com- pelling because the local-environment effects and associated Quantum phase transitions (QPTs), defined as continu- spin-cluster effects are nontrivial, and whether the apparent ous phase transitions at zero temperature, have remained an quantum phase transition is similar to or distinguishable from intriguing research topic [1–6]. There are several types of other examples is intriguing [5]. QPTs, dealing with various classes of materials, such as Thermodynamic phase transitions such as Curie transitions magnets [7–9], superconductors [10], heavy-fermion com- and QPTs have many features in common but also exhibit pounds [11,12], and ferroelectrics [13], and triggered by important differences. A common feature is that both types different control parameters, for example mechanical pres- of transitions are typically described by power laws that relate sure, magnetic or electric fields, and chemical composi- the response of the system to control parameters. Our focus is tion [14–16]. In some solid-solution alloys of type M − T 1 x x on magnetic alloys, where the order parameter (magnetization [2,17,18] magnetic transition-metal elements (T) cause the M) and the susceptibility χ are controlled by the temperature nonmagnetic metal (M) to become a ferromagnet above some T, the magnetic field H, and the chemical composition x. critical concentration x . The chemical disorder in QPT al- c For example, structurally homogeneous ferromagnets near the loys is normally of the substitutional solid-solution type, β γ Curie temperature T obey M ∼ (T –T ) and χ ∼ 1/|T –T | with nearest-neighbor exchange bonds. This paper deals with c c c [24]. The susceptibility diverges near the critical point, and QPTs caused by interstitial modification of an intermetallic this divergence is accompanied by long-range critical fluc- compound. tuations. These fluctuations, observed for example as critical We consider alloys having the composition Co + Sn ν 1 x opalescence in fluids, have correlation length ξ ∼ 1/|T –T | (0 < x 1), where the excess Co (x) enters the 2d interstitial c [24,25]. A major difference is that QPTs reflect quantum- sites in the NiAs structure (Fig. 1)[19,20]. Current research mechanical fluctuations, as contrasted to the thermodynamic on Co-based alloys is partly motivated by the need to discover fluctuations governing the critical behavior of ferromagnets new magnetic materials with high Curie temperature, high (Curie transition) and of fluids (gas-liquid transition). anisotropy, and high magnetization. Such materials, especially The description of critical behavior and the determina- consisting of earth-abundant and inexpensive elements, are tion of critical exponents are nontrivial, especially in low- needed for advanced energy and information-processing ap- dimensional systems [24–27]. For example, it is well known plications [21–23]. New Co- and/or Fe-rich compounds, es- that long-range fluctuations yield T = 0 in one-dimensional pecially those with noncubic and/or metastable structures, are c magnets [25,26,28]. The simplest approach towards critical of particular interest, since they potentially possess the above phenomena is the mean-field approximation (MFA), where the crystalline environment of a given atom is modeled as an effective medium. In this paper, we distinguish between *[email protected] three types of mean-field approximations, namely thermo- †[email protected] dynamic MFA (Landau theory), quantum-mechanical MFA 2469-9950/2019/99(18)/184438(10) 184438-1 ©2019 American Physical Society RABINDRA PAHARI et al. PHYSICAL REVIEW B 99, 184438 (2019) itinerant systems, such as Co-Sn. The corresponding wave- vector-dependent susceptibility is [29,30] χ χ(k) = 0 . (5) 2 1 − ID(EF ) + wk 2 This equation, where w ≈ 2ID(EF )/kF , describes the low- temperature susceptibility. Due to spin fluctuations, Eq. (5)is difficult to generalize to finite temperatures, but for reasons FIG. 1. Unit cell of NiAs-ordered Co1+xSn: (a) CoSn and discussed elsewhere [30–32], high-temperature susceptibili- (b) Co1.5Sn. The excess Co (x) occupies the interstitial 2d sites, ties of itinerant magnets are often of the Curie-Weiss type, which exhibit a trigonal-prismatic coordination by the Co atoms of Eq. (3). the CoSn host lattice. A third type of mean-field theory is related to the per- colation aspect of disordered alloys. Randomly distributing (Stoner theory), and structural MFA (Bethe-lattice percolation Co atoms over the interstitial sites creates Co-rich clusters theory). and Co-poor regions, and ferromagnetism develops from Co- In its simplest form, the mean-field theory of thermody- rich clusters. In fact, even below the onset of long-range = namic phase transitions considers the order parameter M ferromagnetic order, some clusters are very big, which causes Mez and assumes a Landau free energy the susceptibility to exhibit a quasiferromagnetic singularity 1 2 1 4 known as the Griffiths singularity; the corresponding region is F = a0(T − Tc)M + a4M − μ0HM, (1) 2 4 referred to as Griffith phase [2,33–36]. With increasing x,the where a and a are materials constants and M =M(r). 0 4 Co clusters grow, and at some initial percolation threshold xc, Putting ∂F/∂M = 0 in this equation yields the familiar mean- an infinite backbone develops. Below xc, the average cluster field exponents β = 1/2 and γ = 1. An alternative way of size has the character of a correlation length, obeying ξ ∼ deriving these exponents is to replace the field H acting on an ν 1/(xc − x) [37,38]. atomic spin by H + λM, where λ is referred to as molecular- The mean-field description of percolation is that of the or mean-field coefficient. Bethe lattice [38] and yields the mean-field exponent ν = The assumption of an effective medium of average mag- 1/2. The same mean-field exponent is obtained from Eq. (3), netization M does not necessarily mean that the local 1/2 where ξ ∼ 1/(1 − T/Tc ) , and from Eq. (5), where ξ ∼ magnetization M(r) of homogeneous solids is equal to the 1/2 1/[1 − ID(EF )] . These correlation lengths all diverge at average magnetization M. The corresponding fluctuations the critical point. One question considered in this paper is how are described by the correlation function the different correlation lengths interact with each other in the C(|r − r|) = [M(r) −M][M(r) −M]. (2) cobalt-tin system. Our emphasis is on length scales of a few interatomic The zero-field correlations decay as C(|r − r |) ∼ distances, partially going beyond mean-field theory. In the exp(−ξ/(|r − r|)). experimental part, Sec. II, the Co-Sn alloys are investigated Completely ignoring C(|r − r |) corresponds to the Landau using structural and magnetic measurements, whereas Sec. III theory of Eq. (1), but the Ornstein-Zernike extension of the is devoted to analytical and density-functional theoretical Landau theory includes fluctuations on a mean-field level calculations, as well as an analysis of the data in terms of a [24,27]. The extension is obtained by adding a Ginzburg- quantum phase transition.
Load more

Recommended publications
  • Phase Transitions in Quantum Condensed Matter
    Diss. ETH No. 15104 Phase Transitions in Quantum Condensed Matter A dissertation submitted to the SWISS FEDERAL INSTITUTE OF TECHNOLOGY ZURICH¨ (ETH Zuric¨ h) for the degree of Doctor of Natural Science presented by HANS PETER BUCHLER¨ Dipl. Phys. ETH born December 5, 1973 Swiss citizien accepted on the recommendation of Prof. Dr. J. W. Blatter, examiner Prof. Dr. W. Zwerger, co-examiner PD. Dr. V. B. Geshkenbein, co-examiner 2003 Abstract In this thesis, phase transitions in superconducting metals and ultra-cold atomic gases (Bose-Einstein condensates) are studied. Both systems are examples of quantum condensed matter, where quantum effects operate on a macroscopic level. Their main characteristics are the condensation of a macroscopic number of particles into the same quantum state and their ability to sustain a particle current at a constant velocity without any driving force. Pushing these materials to extreme conditions, such as reducing their dimensionality or enhancing the interactions between the particles, thermal and quantum fluctuations start to play a crucial role and entail a rich phase diagram. It is the subject of this thesis to study some of the most intriguing phase transitions in these systems. Reducing the dimensionality of a superconductor one finds that fluctuations and disorder strongly influence the superconducting transition temperature and eventually drive a superconductor to insulator quantum phase transition. In one-dimensional wires, the fluctuations of Cooper pairs appearing below the mean-field critical temperature Tc0 define a finite resistance via the nucleation of thermally activated phase slips, removing the finite temperature phase tran- sition. Superconductivity possibly survives only at zero temperature.
    [Show full text]
  • The Superconductor-Metal Quantum Phase Transition in Ultra-Narrow Wires
    The superconductor-metal quantum phase transition in ultra-narrow wires Adissertationpresented by Adrian Giuseppe Del Maestro to The Department of Physics in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the subject of Physics Harvard University Cambridge, Massachusetts May 2008 c 2008 - Adrian Giuseppe Del Maestro ! All rights reserved. Thesis advisor Author Subir Sachdev Adrian Giuseppe Del Maestro The superconductor-metal quantum phase transition in ultra- narrow wires Abstract We present a complete description of a zero temperature phasetransitionbetween superconducting and diffusive metallic states in very thin wires due to a Cooper pair breaking mechanism originating from a number of possible sources. These include impurities localized to the surface of the wire, a magnetic field orientated parallel to the wire or, disorder in an unconventional superconductor. The order parameter describing pairing is strongly overdamped by its coupling toaneffectivelyinfinite bath of unpaired electrons imagined to reside in the transverse conduction channels of the wire. The dissipative critical theory thus contains current reducing fluctuations in the guise of both quantum and thermally activated phase slips. A full cross-over phase diagram is computed via an expansion in the inverse number of complex com- ponents of the superconducting order parameter (equal to oneinthephysicalcase). The fluctuation corrections to the electrical and thermal conductivities are deter- mined, and we find that the zero frequency electrical transport has a non-monotonic temperature dependence when moving from the quantum critical to low tempera- ture metallic phase, which may be consistent with recent experimental results on ultra-narrow MoGe wires. Near criticality, the ratio of the thermal to electrical con- ductivity displays a linear temperature dependence and thustheWiedemann-Franz law is obeyed.
    [Show full text]
  • Coexistence of Superparamagnetism and Ferromagnetism in Co-Doped
    Available online at www.sciencedirect.com ScienceDirect Scripta Materialia 69 (2013) 694–697 www.elsevier.com/locate/scriptamat Coexistence of superparamagnetism and ferromagnetism in Co-doped ZnO nanocrystalline films Qiang Li,a Yuyin Wang,b Lele Fan,b Jiandang Liu,a Wei Konga and Bangjiao Yea,⇑ aState Key Laboratory of Particle Detection and Electronics, University of Science and Technology of China, Hefei 230026, People’s Republic of China bNational Synchrotron Radiation Laboratory, University of Science and Technology of China, Hefei 230029, People’s Republic of China Received 8 April 2013; revised 5 August 2013; accepted 6 August 2013 Available online 13 August 2013 Pure ZnO and Zn0.95Co0.05O films were deposited on sapphire substrates by pulsed-laser deposition. We confirm that the magnetic behavior is intrinsic property of Co-doped ZnO nanocrystalline films. Oxygen vacancies play an important mediation role in Co–Co ferromagnetic coupling. The thermal irreversibility of field-cooling and zero field-cooling magnetizations reveals the presence of superparamagnetic behavior in our films, while no evidence of metallic Co clusters was detected. The origin of the observed superparamagnetism is discussed. Ó 2013 Acta Materialia Inc. Published by Elsevier Ltd. All rights reserved. Keywords: Dilute magnetic semiconductors; Superparamagnetism; Ferromagnetism; Co-doped ZnO Dilute magnetic semiconductors (DMSs) have magnetic properties in this system. In this work, the cor- attracted increasing attention in the past decade due to relation between the structural features and magnetic their promising technological applications in the field properties of Co-doped ZnO films was clearly of spintronic devices [1]. Transition metal (TM)-doped demonstrated. ZnO is one of the most attractive DMS candidates The Zn0.95Co0.05O films were deposited on sapphire because of its outstanding properties, including room- (0001) substrates by pulsed-laser deposition using a temperature ferromagnetism.
    [Show full text]
  • Solid State Physics 2 Lecture 5: Electron Liquid
    Physics 7450: Solid State Physics 2 Lecture 5: Electron liquid Leo Radzihovsky (Dated: 10 March, 2015) Abstract In these lectures, we will study itinerate electron liquid, namely metals. We will begin by re- viewing properties of noninteracting electron gas, developing its Greens functions, analyzing its thermodynamics, Pauli paramagnetism and Landau diamagnetism. We will recall how its thermo- dynamics is qualitatively distinct from that of a Boltzmann and Bose gases. As emphasized by Sommerfeld (1928), these qualitative di↵erence are due to the Pauli principle of electons’ fermionic statistics. We will then include e↵ects of Coulomb interaction, treating it in Hartree and Hartree- Fock approximation, computing the ground state energy and screening. We will then study itinerate Stoner ferromagnetism as well as various response functions, such as compressibility and conduc- tivity, and screening (Thomas-Fermi, Debye). We will then discuss Landau Fermi-liquid theory, which will allow us understand why despite strong electron-electron interactions, nevertheless much of the phenomenology of a Fermi gas extends to a Fermi liquid. We will conclude with discussion of electrons on the lattice, treated within the Hubbard and t-J models and will study transition to a Mott insulator and magnetism 1 I. INTRODUCTION A. Outline electron gas ground state and excitations • thermodynamics • Pauli paramagnetism • Landau diamagnetism • Hartree-Fock theory of interactions: ground state energy • Stoner ferromagnetic instability • response functions • Landau Fermi-liquid theory • electrons on the lattice: Hubbard and t-J models • Mott insulators and magnetism • B. Background In these lectures, we will study itinerate electron liquid, namely metals. In principle a fully quantum mechanical, strongly Coulomb-interacting description is required.
    [Show full text]
  • Study of Spin Glass and Cluster Ferromagnetism in Rusr2eu1.4Ce0.6Cu2o10-Δ Magneto Superconductor Anuj Kumar, R
    Study of spin glass and cluster ferromagnetism in RuSr2Eu1.4Ce0.6Cu2O10-δ magneto superconductor Anuj Kumar, R. P. Tandon, and V. P. S. Awana Citation: J. Appl. Phys. 110, 043926 (2011); doi: 10.1063/1.3626824 View online: http://dx.doi.org/10.1063/1.3626824 View Table of Contents: http://jap.aip.org/resource/1/JAPIAU/v110/i4 Published by the American Institute of Physics. Related Articles Annealing effect on the excess conductivity of Cu0.5Tl0.25M0.25Ba2Ca2Cu3O10−δ (M=K, Na, Li, Tl) superconductors J. Appl. Phys. 111, 053914 (2012) Effect of columnar grain boundaries on flux pinning in MgB2 films J. Appl. Phys. 111, 053906 (2012) The scaling analysis on effective activation energy in HgBa2Ca2Cu3O8+δ J. Appl. Phys. 111, 07D709 (2012) Magnetism and superconductivity in the Heusler alloy Pd2YbPb J. Appl. Phys. 111, 07E111 (2012) Micromagnetic analysis of the magnetization dynamics driven by the Oersted field in permalloy nanorings J. Appl. Phys. 111, 07D103 (2012) Additional information on J. Appl. Phys. Journal Homepage: http://jap.aip.org/ Journal Information: http://jap.aip.org/about/about_the_journal Top downloads: http://jap.aip.org/features/most_downloaded Information for Authors: http://jap.aip.org/authors Downloaded 12 Mar 2012 to 14.139.60.97. Redistribution subject to AIP license or copyright; see http://jap.aip.org/about/rights_and_permissions JOURNAL OF APPLIED PHYSICS 110, 043926 (2011) Study of spin glass and cluster ferromagnetism in RuSr2Eu1.4Ce0.6Cu2O10-d magneto superconductor Anuj Kumar,1,2 R. P. Tandon,2 and V. P. S. Awana1,a) 1Quantum Phenomena and Application Division, National Physical Laboratory (CSIR), Dr.
    [Show full text]
  • Ferromagnetic State and Phase Transitions
    Ferromagnetic state and phase transitions Yuri Mnyukh 76 Peggy Lane, Farmington, CT, USA, e-mail: [email protected] (Dated: June 20, 2011) Evidence is summarized attesting that the standard exchange field theory of ferromagnetism by Heisenberg has not been successful. It is replaced by the crystal field and a simple assumption that spin orientation is inexorably associated with the orientation of its carrier. It follows at once that both ferromagnetic phase transitions and magnetization must involve a structural rearrangement. The mechanism of structural rearrangements in solids is nucleation and interface propagation. The new approach accounts coherently for ferromagnetic state and its manifestations. 1. Weiss' molecular and Heisenberg's electron Its positive sign led to a collinear ferromagnetism, and exchange fields negative to a collinear antiferromagnetism. Since then it has become accepted that Heisenberg gave a quantum- Generally, ferromagnetics are spin-containing materials mechanical explanation for Weiss' "molecular field": that are (or can be) magnetized and remain magnetized "Only quantum mechanics has brought about in the absence of magnetic field. This definition also explanation of the true nature of ferromagnetism" includes ferrimagnetics, antiferromagnetics, and (Tamm [2]). "Heisenberg has shown that the Weiss' practically unlimited variety of magnetic structures. theory of molecular field can get a simple and The classical Weiss / Heisenberg theory of straightforward explanation in terms of quantum ferromagnetism, taught in the universities and presented mechanics" (Seitz [1]). in many textbooks (e. g., [1-4]), deals basically with the special case of a collinear (parallel and antiparallel) spin arrangement. 2. Inconsistence with the reality The logic behind the theory in question is as follows.
    [Show full text]
  • Quantum Phase Transitions
    INSTITUTE OF PHYSICS PUBLISHING REPORTS ON PROGRESS IN PHYSICS Rep. Prog. Phys. 66 (2003) 2069–2110 PII: S0034-4885(03)33852-7 Quantum phase transitions Matthias Vojta Institut fur¨ Theorie der Kondensierten Materie, Universitat¨ Karlsruhe, Postfach 6980, D-76128 Karlsruhe, Germany E-mail: [email protected] Received 1 August 2003, in final form 8 October 2003 Published 3 November 2003 Online at stacks.iop.org/RoPP/66/2069 Abstract In recent years, quantum phase transitions have attracted the interest of both theorists and experimentalists in condensed matter physics. These transitions, which are accessed at zero temperature by variation of a non-thermal control parameter, can influence the behaviour of electronic systems over a wide range of the phase diagram. Quantum phase transitions occur as a result of competing ground state phases. The cuprate superconductors which can be tuned from a Mott insulating to a d-wave superconducting phase by carrier doping are a paradigmatic example. This review introduces important concepts of phase transitions and discusses the interplay of quantum and classical fluctuations near criticality. The main part of the article is devoted to bulk quantum phase transitions in condensed matter systems. Several classes of transitions will be briefly reviewed, pointing out, e.g., conceptual differences between ordering transitions in metallic and insulating systems. An interesting separate class of transitions is boundary phase transitions where only degrees of freedom of a subsystem become critical; this will be illustrated in a few examples. The article is aimed at bridging the gap between high- level theoretical presentations and research papers specialized in certain classes of materials.
    [Show full text]
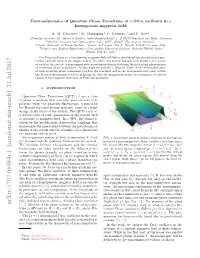
  • Thermodynamics of Quantum Phase Transitions of a Dirac Oscillator in a Homogenous Magnetic field
    Thermodynamics of Quantum Phase Transitions of a Dirac oscillator in a homogenous magnetic field A. M. Frassino,1 D. Marinelli,2 O. Panella,3 and P. Roy4 1Frankfurt Institute for Advanced Studies, Ruth-Moufang-Straße 1, D-60438 Frankfurt am Main, Germany 2Machine Learning and Optimization Lab., RIST, 400487 Cluj-Napoca, Romania∗ 3Istituto Nazionale di Fisica Nucleare, Sezione di Perugia, Via A. Pascoli, I-06123 Perugia, Italyy 4Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata-700108, India (Dated: July 24, 2017) The Dirac oscillator in a homogenous magnetic field exhibits a chirality phase transition at a par- ticular (critical) value of the magnetic field. Recently, this system has also been shown to be exactly solvable in the context of noncommutative quantum mechanics featuring the interesting phenomenon of re-entrant phase transitions. In this work we provide a detailed study of the thermodynamics of such quantum phase transitions (both in the standard and in the noncommutative case) within the Maxwell-Boltzmann statistics pointing out that the magnetization has discontinuities at critical values of the magnetic field even at finite temperatures. I. INTRODUCTION Quantum Phase Transitions (QPT) [1] are a class of phase transitions that can take place at zero tem- perature when the quantum fluctuations, required by the Heisenberg's uncertainty principle, cause an abrupt change in the phase of the system. The QPTs occur at a critical value of some parameters of the system such as pressure or magnetic field. In a QPT, the change is driven by the modification of particular couplings that characterise the interactions between the microscopic el- ements of the system and the dynamics of its phase near the quantum critical point.
    [Show full text]
  • Heavy Fermions and Quantum Phase Transitions Qimiao Si and Frank Steglich
    REVIEW non-Fermi liquid behavior (9), which goes beyond the standard theory of metals [Fermi- liquid theory (10)], is another phenomenon that is Heavy Fermions and broadly relevant to the physics of strongly cor- related systems (11, 12). Quantum Phase Transitions Quantum criticality has been implicated to one degree or another in a host of other heavy- fermion metals (4, 13, 14). These include CeCu2Si2, 1 2 Qimiao Si * and Frank Steglich * the first superconductor to be observed among heavy-fermion metals (15), and CeRhIn5 (Fig. Quantum phase transitions arise in many-body systems because of competing interactions that promote 1C) (16). Extensive theoretical studies have led – rivaling ground states. Recent years have seen the identification of continuous quantum phase transitions, to unconventional quantum criticality (17 20). or quantum critical points, in a host of antiferromagnetic heavy-fermion compounds. Studies of the More recently, a plethora of phases have been interplay between the various effects have revealed new classes of quantum critical points and are uncovered in heavy-fermion metals near a QCP b uncovering a plethora of new quantum phases. At the same time, quantum criticality has provided [such as in Ir-doped YbRh2Si2 (8)andin -YbAlB4 fresh insights into the electronic, magnetic, and superconducting properties of the heavy-fermion metals. (21)]. Together with the theoretical studies of the We review these developments, discuss the open issues, and outline some directions for future research. global phase diagram of the heavy-fermion metals (22, 2), these developments open up an entirely new frontier on the interplay between quantum critical- uantum mechanics not only governs the uent particles.
    [Show full text]
  • Band Ferromagnetism in Systems of Variable Dimensionality
    JOURNAL OF OPTOELECTRONICS AND ADVANCED MATERIALS Vol. 10, No. 11, November 2008, p.3058 - 3068 Band ferromagnetism in systems of variable dimensionality C. M. TEODORESCU*, G. A. LUNGU National Institute of Materials Physics, Atomistilor 105b, P.O. Box MG-7, RO-77125 Magurele-Ilfov, Romania The Stoner instability of the paramagnetic state, yielding to the occurence of ferromagnetism, is reviewed for electron density of states reflecting changes in the dimensionality of the system. The situations treated are one-dimensional (1D), two-dimensional (2D) and three-dimensional (3D) cases and also a special case where the density of states has a parabolic shape near the Fermi level, and is half-filled at equilibrium. We recover the basic results obtained in the original work of E.C. Stoner [Proc. Roy. Soc. London A 165, 372 (1938)]; also we demonstrate that in 1D and 2D case, whenever the Stoner criterion is satisfied, the system evolves spontaneously towards maximum polarization allowed by Hund's rules. For the 3D case, the situation is that: (i) when the Stoner criterion is satisfied, but the ratio between the Hubbard repulsion energy and the Fermi energy is between 4/3 and 3/2, the system evolves towards a ferromagnetic state with incomplete polarization (the polarization parameter is between 0 and 1); (ii) when , the system evolves towards maximum polarization. This situation was also recognized in the original paper of Stoner, but with no further analysis of the obtained polarizations nor comparison with experimental results. We apply the result of calculation in order to predict the Hubbard interaction energy.
    [Show full text]
  • Condensed Matter Option MAGNETISM Handout 1
    Condensed Matter Option MAGNETISM Handout 1 Hilary 2014 Radu Coldea http://www2.physics.ox.ac.uk/students/course-materials/c3-condensed-matter-major-option Syllabus The lecture course on Magnetism in Condensed Matter Physics will be given in 7 lectures broken up into three parts as follows: 1. Isolated Ions Magnetic properties become particularly simple if we are able to ignore the interactions between ions. In this case we are able to treat the ions as effectively \isolated" and can discuss diamagnetism and paramagnetism. For the latter phenomenon we revise the derivation of the Brillouin function outlined in the third-year course. Ions in a solid interact with the crystal field and this strongly affects their properties, which can be probed experimentally using magnetic resonance (in particular ESR and NMR). 2. Interactions Now we turn on the interactions! I will discuss what sort of magnetic interactions there might be, including dipolar interactions and the different types of exchange interaction. The interactions lead to various types of ordered magnetic structures which can be measured using neutron diffraction. I will then discuss the mean-field Weiss model of ferromagnetism, antiferromagnetism and ferrimagnetism and also consider the magnetism of metals. 3. Symmetry breaking The concept of broken symmetry is at the heart of condensed matter physics. These lectures aim to explain how the existence of the crystalline order in solids, ferromagnetism and ferroelectricity, are all the result of symmetry breaking. The consequences of breaking symmetry are that systems show some kind of rigidity (in the case of ferromagnetism this is permanent magnetism), low temperature elementary excitations (in the case of ferromagnetism these are spin waves, also known as magnons), and defects (in the case of ferromagnetism these are domain walls).
    [Show full text]
  • The Spinor Bose-Einstein Condensate: a Dipolar Magnetic Superfluid
    Ψ TThhee SSppiinnoorr BBoossee--EEiinnsstteeiinn CCoonnddeennssaattee:: AA DDiippoollaarr MMaaggnneettiicc SSuuppeerrfflluuiidd Dan Stamper-Kurn UC Berkeley, Physics Lawrence Berkeley National Laboratory, Materials Sciences Ψ Spinor gases mF = 2 Energy mF = 1 F=2 mF = 0 magnetically Optically m = -1 F trappable trapped F=2 m = -2 spinor gas F mF = -1 F=1 mF = 0 Optically mF = 1 trapped F=1 spinor gas B What do we want to know? ≈ χ χ χ ’ ≈ ρ ρ ρ ’ + + + + − +1,+1 +1,0 +1,−1 ∆ σ ,σ σ ,π σ ,σ ÷ ∆ ÷ ρ = ρ ρ ρ χ = ∆ χ + χ χ − ÷ ∆ 0,+1 0,0 0,−1 ÷ π ,σ π ,π π ,σ ∆ρ ρ ρ ÷ ∆ ÷ « −1,+1 −1,0 −1,−1 ◊ ∆χ − + χ − χ − − ÷ « σ ,σ σ ,π σ ,σ ◊ FC F = cosθ spin F m=1 coh erences y φ “orientation” x nematicity N m=2 coh erences “alignment” θ θ iφ −iφ ’ R∆e cos m =1 − e sin m = −1 ÷ « 2 2 ◊ + F′ = 2 1 1 1 12 2 2 y F =1 z x in this case small signal 2 (# photons/pixel) = + ( + + ε ) S Nγ 1 A ( 1) Fy Fy ⁄ ∝ n2D Direct imaging of Larmor precession m 0 0 3 l a n g i s t s a r t n y o F c 0.5 - ~ e s a h p 0 k a e time (50 s/frame) P Aliased sampling: 2 x 20 kHz – Observed rate = 38.097(15) kHz Spinor gas magnetometry B N atoms F F F φ Probe: t = 0 t = τ N N 0 0 N N B 0 1 N N 0 0 t = 0 t = τ > 1 ’ 1 1 Area-resolving: ∆B = ∆ ÷× = S × ∆ µ ÷ A « g B DTcoh n2 D ◊ Ttotal A Ttotal A Ψ Experimental demonstration Clarify fundamental and technical limits on precision single-particle and collective light scattering, experimental tricks unbiased phase estimation methods Measure background noise confirm areal and temporal scaling of sensitivity Measure localized magnetic field quantum-mechanical diffusion of magnetization actually measure limits to dynamic range magnetic background field with uncontrolled long-range inhomogeneities actually measure fictitious Z eeman shift from focused, off- resonance laser Ψ %F&ield“ measurements B AC Stark shift = “Fictitious” magnetic field Comparing atoms & SQUIDs Existing low freq.
    [Show full text]