DOCSLIB.ORG

Priestley Duality for MV-Algebras: a New Perspective

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Priestley Duality for MV-Algebras: a New Perspective Priestley duality for MV-algebras: A new perspective Wesley Fussner (joint work with Mai Gehrke, Sam van Gool, and Vincenzo Marra) CNRS, France Shanks Workshop on Ordered Algebras and Logic Nashville, TN, USA 7 March 2020 1 / 36 DRAFT 2 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. Outline 2 / 36 DRAFT 2 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. Outline 1 Priestley duality as usually presented. 2 / 36 DRAFT 2 3 Priestley duality via the canonical extension. 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. Outline 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 2 / 36 DRAFT 2 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. Outline 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 2 / 36 DRAFT 2 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. Outline 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 4 -algebras. 2 / 36 DRAFT 2 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. Outline 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 2 / 36 DRAFT 2 7 Specializing this to MV-algebras. Outline 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 2 / 36 DRAFT 2 Outline 1 Priestley duality as usually presented. 2 Canonical extensions of bounded distributive lattices. 3 Priestley duality via the canonical extension. 4 -algebras. 5 Priestley duality for -algebras by their canonical extensions. 6 Splitting of the operation on duals to obtain a more expressive environment. 7 Specializing this to MV-algebras. 2 / 36 DRAFT 2 Part I: Priestley duality and canonical extensions 3 / 36 DRAFT 2 Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: Priestley spaces 4 / 36 DRAFT 2 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 4 / 36 DRAFT 2 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 4 / 36 DRAFT 2 Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. 4 / 36 DRAFT 2 If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: 4 / 36 DRAFT 2 The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion. 4 / 36 DRAFT 2 , where a^ = fx 2 X (L): a 2 xg: Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg 4 / 36 DRAFT 2 Priestley spaces Definition: A Priestley space is an ordered topological space (X ; ≤; τ) such that: 1 (X ; τ) is compact, and 2 for every x; y 2 X with x 6≤ y, there exists a clopen down-set U ⊆ X such that x 62 U, y 2 U. Generic example: If L = (L; ^; _; 0; 1) is a bounded distributive lattice, then the set of prime ideals X (L) of L is a Priestley space ordered by inclusion.The topology is generated by the clopen subbasis fa^; (^a)c : a 2 Lg, where a^ = fx 2 X (L): a 2 xg: 4 / 36 DRAFT 2 The correspondence L 7! X (L) may be lifted to (one functor of) an equivalence of categories between bounded distributive lattices and Priestley spaces (with continuous isotone maps). Maps h: L1 ! L2 are sent to continuous isotone maps −1 X (L2) ! X (L1) given by h 7! h [−]. The reverse functor takes a Priestley space to its bounded distributive lattice of clopen down-sets. Residuated operations · on BDLs can be captured by ternary relations that amount to the downward-closure (in X (L)) of their complex products: R(x; y; z) () x ⊆ #fa · b : a 2 y; b 2 zg: Priestley duality 5 / 36 DRAFT 2 Maps h: L1 ! L2 are sent to continuous isotone maps −1 X (L2) ! X (L1) given by h 7! h [−]. The reverse functor takes a Priestley space to its bounded distributive lattice of clopen down-sets. Residuated operations · on BDLs can be captured by ternary relations that amount to the downward-closure (in X (L)) of their complex products: R(x; y; z) () x ⊆ #fa · b : a 2 y; b 2 zg: Priestley duality The correspondence L 7! X (L) may be lifted to (one functor of) an equivalence of categories between bounded distributive lattices and Priestley spaces (with continuous isotone maps). 5 / 36 DRAFT 2 The reverse functor takes a Priestley space to its bounded distributive lattice of clopen down-sets. Residuated operations · on BDLs can be captured by ternary relations that amount to the downward-closure (in X (L)) of their complex products: R(x; y; z) () x ⊆ #fa · b : a 2 y; b 2 zg: Priestley duality The correspondence L 7! X (L) may be lifted to (one functor of) an equivalence of categories between bounded distributive lattices and Priestley spaces (with continuous isotone maps).
Load more

Recommended publications
  • Bitopological Duality for Distributive Lattices and Heyting Algebras
    BITOPOLOGICAL DUALITY FOR DISTRIBUTIVE LATTICES AND HEYTING ALGEBRAS GURAM BEZHANISHVILI, NICK BEZHANISHVILI, DAVID GABELAIA, ALEXANDER KURZ Abstract. We introduce pairwise Stone spaces as a natural bitopological generalization of Stone spaces—the duals of Boolean algebras—and show that they are exactly the bitopolog- ical duals of bounded distributive lattices. The category PStone of pairwise Stone spaces is isomorphic to the category Spec of spectral spaces and to the category Pries of Priestley spaces. In fact, the isomorphism of Spec and Pries is most naturally seen through PStone by first establishing that Pries is isomorphic to PStone, and then showing that PStone is isomorphic to Spec. We provide the bitopological and spectral descriptions of many algebraic concepts important for the study of distributive lattices. We also give new bitopo- logical and spectral dualities for Heyting algebras, thus providing two new alternatives to Esakia’s duality. 1. Introduction It is widely considered that the beginning of duality theory was Stone’s groundbreaking work in the mid 30s on the dual equivalence of the category Bool of Boolean algebras and Boolean algebra homomorphism and the category Stone of compact Hausdorff zero- dimensional spaces, which became known as Stone spaces, and continuous functions. In 1937 Stone [33] extended this to the dual equivalence of the category DLat of bounded distributive lattices and bounded lattice homomorphisms and the category Spec of what later became known as spectral spaces and spectral maps. Spectral spaces provide a generalization of Stone 1 spaces. Unlike Stone spaces, spectral spaces are not Hausdorff (not even T1) , and as a result, are more difficult to work with.
    [Show full text]
  • Bitopological Duality for Distributive Lattices and Heyting Algebras
    BITOPOLOGICAL DUALITY FOR DISTRIBUTIVE LATTICES AND HEYTING ALGEBRAS GURAM BEZHANISHVILI, NICK BEZHANISHVILI, DAVID GABELAIA, ALEXANDER KURZ Abstract. We introduce pairwise Stone spaces as a natural bitopological generalization of Stone spaces—the duals of Boolean algebras—and show that they are exactly the bitopolog- ical duals of bounded distributive lattices. The category PStone of pairwise Stone spaces is isomorphic to the category Spec of spectral spaces and to the category Pries of Priestley spaces. In fact, the isomorphism of Spec and Pries is most naturally seen through PStone by first establishing that Pries is isomorphic to PStone, and then showing that PStone is isomorphic to Spec. We provide the bitopological and spectral descriptions of many alge- braic concepts important for the study of distributive lattices. We also give new bitopological and spectral dualities for Heyting algebras, co-Heyting algebras, and bi-Heyting algebras, thus providing two new alternatives of Esakia’s duality. 1. Introduction It is widely considered that the beginning of duality theory was Stone’s groundbreaking work in the mid 30ies on the dual equivalence of the category Bool of Boolean algebras and Boolean algebra homomorphism and the category Stone of compact Hausdorff zero- dimensional spaces, which became known as Stone spaces, and continuous functions. In 1937 Stone [28] extended this to the dual equivalence of the category DLat of bounded distributive lattices and bounded lattice homomorphisms and the category Spec of what later became known as spectral spaces and spectral maps. Spectral spaces provide a generalization of Stone 1 spaces. Unlike Stone spaces, spectral spaces are not Hausdorff (not even T1) , and as a result, are more difficult to work with.
    [Show full text]
  • Arxiv:1906.03640V1 [Math.GN]
    THE FRAME OF NUCLEI OF AN ALEXANDROFF SPACE F. AVILA,´ G. BEZHANISHVILI, P. J. MORANDI, A. ZALD´IVAR Abstract. Let OS be the frame of open sets of a topological space S, and let N(OS) be the frame of nuclei of OS. For an Alexandroff space S, we prove that N(OS) is spatial iff the infinite binary tree T2 does not embed isomorphically into (S, ≤), where ≤ is the specialization preorder of S. 1. Introduction Nuclei play an important role in pointfree topology as they characterize homomorphic images of frames (or dually sublocales of locales). For a frame L, let N(L) be the frame of nuclei of L, also known as the assembly of L. The frame N(L) has been investigated by many authors; see, e.g., [7, 10, 16, 2, 17, 13, 12, 14, 11, 20, 15, 6, 3, 19, 4] (which are listed in chronological order). For example, Beazer and Macnab [2] gave a necessary and sufficient condition for N(L) to be boolean; Niefield and Rosenthal [14] gave necessary and sufficient conditions for N(L) to be spatial, and derived that if N(L) is spatial, then so is L; Simmons [17] proved that if L is the frame of opens of a T0-space S, then N(L) is boolean iff S is scattered; and Isbell [11] proved that if L is the frame of opens of a sober space S, then N(L) is spatial iff S is weakly scattered (see Section 2 for definitions). In [6] the study of N(L) using the spectrum of L was initiated.
    [Show full text]
  • Spectral Sets
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector JOURNAL OF PURE AND APPLIED ALGEBRA ELSE&R Journal of Pure and Applied Algebra 94 (1994) lOlL114 Spectral sets H.A. Priestley Mathematical Institute, 24129 St. Giles, Oxford OXI 3LB, United Kingdom Communicated by P.T. Johnstone; received 17 September 1993; revised 13 April 1993 Abstract The purpose of this expository note is to draw together and to interrelate a variety of characterisations and examples of spectral sets (alias representable posets or profinite posets) from ring theory, lattice theory and domain theory. 1. Introduction Thanks to their threefold incarnation-in ring theory, in lattice theory and in computer science-the structures we wish to consider have been approached from a variety of perspectives, with rather little overlap. We shall seek to show how the results of these independent studies are related, and add some new results en route. We begin with the definitions which will allow us to present, as Theorem 1.1, the amalgam of known results which form the starting point for our later discussion. The theorem collects together ways of describing the prime spectra of commutative rings with identity or, equivalently, of distributive lattices with 0 and 1. A topology z on a set X is defined to be spectral (and (X; s) called a spectral space) if the following conditions hold: (i) ? is sober (that is, every non-empty irreducible closed set is the closure of a unique point), (ii) z is quasicompact, (iii) the quasicompact open sets form a basis for z, (iv) the family of quasicompact open subsets of X is closed under finite intersections.
    [Show full text]
  • Stone Duality for Relations
    Stone Duality for Relations Alexander Kurz, Drew Moshier∗, Achim Jung AMS Sectional Meeting, UC Riverside November 2019 Dual Relations Given a topological space extended with I an equivalence relation or partial order, what is the algebraic structure dual to the quotient of the space? I a non-deterministic computation (relation), what is the dual structure of pre- and post-conditions? Given an algebraic structure extended with I relations, what is the topological dual? Given an (in)equational calculus of logical operations extended with I a Gentzen-style consequence relation, what is its dual semantics for which it is sound and complete? A Motivating Example: Cantor Space Cantor Space C : Excluded middle third subspace of the unit interval. Equivalence relation ≡ glues together the endpoints of the gaps. Dual of C: Free Boolean algebra FrBA(N) over countably many generators. How is ≡ reflected in FrBA(N)? Does this give rise to [0; 1] as the dual of (FrBA(N);:::)? This talk concentrates on the first question. The second question is the subject of another talk. Example: Priestley Spaces Consider C equipped with natural order ≤. I Two clopens a; b are in the dual of ≤ if "a ⊆ b I The reflexive elements "a ⊆ a are the upper clopens I (C; ≤) is the coinserter of C wrt to ≤ I The dual of (C; ≤) is the distributive lattice of reflexive elements I The dual of (C; ≤) is the inserter of the dual of C wrt to the dual of ≤ These are examples of general phenomena that require topological relations. I Every compact Hausdorff space is a quotient of a Stone space I Priestley spaces (the duals of distributive lattices) are strongly order separated ordered Stone spaces.
    [Show full text]
  • Bitopological Vietoris Spaces and Positive Modal Logic∗
    Bitopological Vietoris spaces and positive modal logic∗ Frederik M¨ollerstr¨omLauridsen† Abstract Using the isomorphism from [3] between the category Pries of Priest- ley spaces and the category PStone of pairwise Stone spaces we construct a Vietoris hyperspace functor on the category PStone related to the Vi- etoris hyperspace functor on the category Pries [4, 18, 24]. We show that the coalgebras for this functor determine a semantics for the positive frag- ment of modal logic. The sole novelty of the present work is the explicit construction of the Vietoris hyperspace functor on the category PStone as well as the phrasing of otherwise well-known results in a bitopological language. ∗This constitutes the final report for a individual project under the supervision of Nick Bezhanishvili at the Institute of Logic, Language and Computation. †[email protected] Contents 1 Introduction1 2 Pairwise Stone spaces and Priestley spaces2 3 Hyperspaces of Priestley space5 3.1 The construction of the functor V ∶ Pries → Pries .........7 4 Hyperspace of Pairwise Stone space 10 4.1 The construction of the functor Vbi .................. 11 4.2 The relation between V and Vbi .................... 14 5 Positive modal logic 16 5.1 Duality theory for positive modal logic................ 18 6 The Coalgebraic view 21 6.1 Coalgebras for the bi-Vietoris functor Vbi .............. 22 6.1.1 From relations to coalgebras.................. 22 6.1.2 From coalgebras to relations.................. 23 7 Intuitionistic modal logic 25 A General (bi)topological results 28 1 1 Introduction 1 Introduction A celebrated theorem by Marshall Stone [22] from 1936 states that the category of Boolean algebras and Boolean algebra homomorphisms is dually equivalent to the category of Stone spaces, i.e.
    [Show full text]
  • Department of Mathematics, Increst, Bd. Pacii 220, 79622 Bucharest, Romania 1. 1)]Relimin~Ries Iaemma 1
    Discrete Mathematics 49 (1984) 117-120 117 North-Holland A TOPOLOGICAL CHARACTERIZATION OF COMP~ DISTRIBUTIVE LATrICES Lucian BEZNEA Department of Mathematics, Increst, Bd. Pacii 220, 79622 Bucharest, Romania Received 15 July 1983 An ordered compact space is a compact topological space X, endowed with a partially ordered relation, whose graph is a closed set of X x X (of. [4]). An important subclass of these spaces is that of Priest/ey spaces, characterized by the following property: for every x, y ~X with x~y there is an increasing ciopen set A (i.e. A is closed and open and such that a e A, a ~<z implies that z ~ A) which separates x from y, i.e., x ~ A and y¢~ A. It is known (eft. [5, 6]) that there is a dual equivalence between the category Ldl01 of distributive lattices with least and greatest element and the category IP of Priestley spaces. In this paper we shall prove that a lattice L ~Ld01 is complete if and only if the associated Priestley space X verifies the condition: (EO) De_X, D is increasing and open implies/5" is increasing clopen (where A* denotes the least increasing set which includes A). This result generalizes a welt-known characterization of complete Boolean algebras in terms of associated Stone spaces (see [2, Ch. 11-I, Section 4, 1.emma 1], for instance). We shall also prove that an ordered compact space that fulfils rE0) is necessarily a Priestley space. 1. 1)]relimin~ries The results concerning ordered topological spaces are taken from [4] and those about Priesfley spaces are from [1].
    [Show full text]
  • A Topological Approach to Recognition Mai Gehrke, Serge Grigorieff, Jean-Eric Pin
    A Topological Approach to Recognition Mai Gehrke, Serge Grigorieff, Jean-Eric Pin To cite this version: Mai Gehrke, Serge Grigorieff, Jean-Eric Pin. A Topological Approach to Recognition. ICALP 2010, Jul 2010, Bordeaux, France. pp.151 - 162, 10.1007/978-3-642-14162-1_13. hal-01101846 HAL Id: hal-01101846 https://hal.archives-ouvertes.fr/hal-01101846 Submitted on 9 Jan 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A topological approach to recognition Mai Gehrke1, Serge Grigorieff2, and Jean-Eric´ Pin2⋆ 1 Radboud University Nijmegen, The Netherlands 2 LIAFA, University Paris-Diderot and CNRS, France. Abstract. We propose a new approach to the notion of recognition, which departs from the classical definitions by three specific features. First, it does not rely on automata. Secondly, it applies to any Boolean algebra (BA) of subsets rather than to individual subsets. Thirdly, topol- ogy is the key ingredient. We prove the existence of a minimum recognizer in a very general setting which applies in particular to any BA of subsets of a discrete space. Our main results show that this minimum recognizer is a uniform space whose completion is the dual of the original BA in Stone-Priestley duality; in the case of a BA of languages closed under quotients, this completion, called the syntactic space of the BA, is a com- pact monoid if and only if all the languages of the BA are regular.
    [Show full text]
  • Priestley Duality for Strong Proximity Lattices
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Electronic Notes in Theoretical Computer Science 158 (2006) 199–217 www.elsevier.com/locate/entcs Priestley Duality for Strong Proximity Lattices Mohamed A. El-Zawawy1 Achim Jung2 School of Computer Science University of Birmingham Edgbaston, Birmingham, B15 2TT, UK Abstract In 1937 Marshall Stone extended his celebrated representation theorem for Boolean algebras to dis- tributive lattices. In modern terminology, the representing topological spaces are zero-dimensional stably compact, but typically not Hausdorff. In 1970, Hilary Priestley realised that Stone’s topology could be enriched to yield order-disconnected compact ordered spaces. In the present paper, we generalise Priestley duality to a representation theorem for strong prox- imity lattices. For these a “Stone-type” duality was given in 1995 in joint work between Philipp S¨underhauf and the second author, which established a close link between these algebraic struc- tures and the class of all stably compact spaces. The feature which distinguishes the present work from this duality is that the proximity relation of strong proximity lattices is “preserved” in the dual, where it manifests itself as a form of “apartness.” This suggests a link with constructive mathematics which in this paper we can only hint at. Apartness seems particularly attractive in view of potential applications of the theory in areas of semantics where continuous phenomena play a role; there, it is the distinctness between different states which is observable, not equality. The idea of separating states is also taken up in our discussion of possible morphisms for which the representation theorem extends to an equivalence of categories.
    [Show full text]
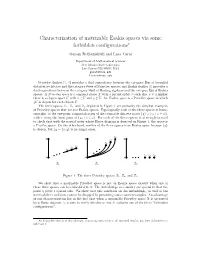
  • Characterization of Metrizable Esakia Spaces Via Some Forbidden Configurations∗
    Characterization of metrizable Esakia spaces via some forbidden configurations∗ Guram Bezhanishvili and Luca Carai Department of Mathematical sciences New Mexico State University Las Cruces NM 88003, USA [email protected] [email protected] Priestley duality [3,4] provides a dual equivalence between the category Dist of bounded distributive lattices and the category Pries of Priestley spaces; and Esakia duality [1] provides a dual equivalence between the category Heyt of Heyting algebras and the category Esa of Esakia spaces. A Priestley space is a compact space X with a partial order ≤ such that x 6≤ y implies there is a clopen upset U with x 2 U and y2 = U. An Esakia space is a Priestley space in which #U is clopen for each clopen U. The three spaces Z1, Z2, and Z3 depicted in Figure1 are probably the simplest examples of Priestley spaces that are not Esakia spaces. Topologically each of the three spaces is home- omorphic to the one-point compactification of the countable discrete space fyg [ fzn j n 2 !g, with x being the limit point of fzn j n 2 !g. For each of the three spaces, it is straightforward to check that with the partial order whose Hasse diagram is depicted in Figure1, the space is a Pristley space. On the other hand, neither of the three spaces is an Esakia space because fyg is clopen, but #y = fx; yg is no longer open. z y y 0 y z1 z2 z0 z1 z2 z z z x x x 2 1 0 Z1 Z2 Z3 Figure 1: The three Priestley spaces Z1, Z2, and Z3.
    [Show full text]
  • Priestley Dualities for Some Lattice-Ordered Algebraic Structures, Including MTL, IMTL and MV-Algebras∗
    DOI: 10.2478/s11533-006-0025-6 Research article CEJM 4(4) 2006 600–623 Priestley dualities for some lattice-ordered algebraic structures, including MTL, IMTL and MV-algebras∗ Leonardo Manuel Cabrer†, Sergio Arturo Celani‡, Departamento de Matem´aticas, Facultad de Ciencias Exactas, Universidad Nacional del Centro, Pinto 399, 7000 Tandil, Argentina Received 13 July 2005; accepted 13 June 2006 Abstract: In this work we give a duality for many classes of lattice ordered algebras, as Integral Commutative Distributive Residuated Lattices MTL-algebras, IMTL-algebras and MV-algebras (see page 604). These dualities are obtained by restricting the duality given by the second author for DLFI- algebras by means of Priestley spaces with ternary relations (see [2]). We translate the equations that define some known subvarieties of DLFI-algebras to relational conditions in the associated DLFI-space. c Versita Warsaw and Springer-Verlag Berlin Heidelberg. All rights reserved. Keywords: Bounded distributive lattices with fusion and implication, Priestley duality, residuated distributive lattices, MTL-algebras, IMTL-algebras, MV-algebras MSC (2000): 03G10, 03B50, 06D35,06D72 1 Introduction In recent years many varieties of algebras associated to multi-valued logics have been introduced . The majority of these algebras are commutative integral distributive resid- uated lattices [8] with additional conditions, as for example, the variety of MV-algebras [4], the variety of BL-algebras, and the varieties of MTL-algebras and ITML-algebras [5, 6], recently introduced. All these classes of algebras are bounded distributive lattices with two additional binary operations ◦ and → satisfying special conditions. On the other hand, in [2], the varieties DLF of DLF-algebras, DLI of DLI-algebras and DLFI ∗ The authors are supported by the Agentinian Consejo de Investigaciones Cientificas y Tecnicas (CON- ICET).
    [Show full text]
  • Duality Theory for Enriched Priestley Spaces
    Duality theory for enriched Priestley spaces Dirk Hofmann and Pedro Nora∗ Center for Research and Development in Mathematics and Applications, Department of Mathematics, University of Aveiro, Portugal. Friedrich-Alexander-Universität Erlangen-Nürnberg, Germany. [email protected], [email protected] The term Stone-type duality often refers to a dual equivalence between a category of lattices or other partially ordered structures on one side and a category of topo- logical structures on the other. This paper is part of a larger endeavour that aims to extend a web of Stone-type dualities from ordered to metric structures and, more generally, to quantale-enriched categories. In particular, we improve our previous work and show how certain duality results for categories of [0, 1]-enriched Priest- ley spaces and [0, 1]-enriched relations can be restricted to functions. In a broader context, we investigate the category of quantale-enriched Priestley spaces and contin- uous functors, with emphasis on those properties which identify the algebraic nature of the dual of this category. 1 Introduction Naturally, the starting point of our investigation of Stone-type dualities is Stone’s classical 1936 duality result (1.i) BooSp ∼ BAop for Boolean algebras and homomorphisms together with its generalisation Spec ∼ DLop to distributive lattices and homomorphisms obtained shortly afterwards in [Stone, 1938]. Here BooSp denotes the category of Boolean spaces1 and continuous maps, and Spec the category of spectral spaces and spectral maps (see also [Hochster, 1969]). In this paper we will often work ∗This work is supported by the ERDF – European Regional Development Fund through the Operational Pro- gramme for Competitiveness and Internationalisation – COMPETE 2020 Programme, by German Research Council (DFG) under project GO 2161/1-2, and by The Center for Research and Development in Mathematics and Applications (CIDMA) through the Portuguese Foundation for Science and Technology (FCT – Fundação para a Ciência e a Tecnologia), references UIDB/04106/2020 and UIDP/04106/2020.
    [Show full text]