Unraveling the Genetics of Human Diseases by Integrating Patterns for Epistasis Detection an Honors Thesis Submitted to the Depa
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bioinformatics Analyses of Genomic Imprinting
Bioinformatics Analyses of Genomic Imprinting Dissertation zur Erlangung des Grades des Doktors der Naturwissenschaften der Naturwissenschaftlich-Technischen Fakultät III Chemie, Pharmazie, Bio- und Werkstoffwissenschaften der Universität des Saarlandes von Barbara Hutter Saarbrücken 2009 Tag des Kolloquiums: 08.12.2009 Dekan: Prof. Dr.-Ing. Stefan Diebels Berichterstatter: Prof. Dr. Volkhard Helms Priv.-Doz. Dr. Martina Paulsen Vorsitz: Prof. Dr. Jörn Walter Akad. Mitarbeiter: Dr. Tihamér Geyer Table of contents Summary________________________________________________________________ I Zusammenfassung ________________________________________________________ I Acknowledgements _______________________________________________________II Abbreviations ___________________________________________________________ III Chapter 1 – Introduction __________________________________________________ 1 1.1 Important terms and concepts related to genomic imprinting __________________________ 2 1.2 CpG islands as regulatory elements ______________________________________________ 3 1.3 Differentially methylated regions and imprinting clusters_____________________________ 6 1.4 Reading the imprint __________________________________________________________ 8 1.5 Chromatin marks at imprinted regions___________________________________________ 10 1.6 Roles of repetitive elements ___________________________________________________ 12 1.7 Functional implications of imprinted genes _______________________________________ 14 1.8 Evolution and parental conflict ________________________________________________ -

Noelia Díaz Blanco
Effects of environmental factors on the gonadal transcriptome of European sea bass (Dicentrarchus labrax), juvenile growth and sex ratios Noelia Díaz Blanco Ph.D. thesis 2014 Submitted in partial fulfillment of the requirements for the Ph.D. degree from the Universitat Pompeu Fabra (UPF). This work has been carried out at the Group of Biology of Reproduction (GBR), at the Department of Renewable Marine Resources of the Institute of Marine Sciences (ICM-CSIC). Thesis supervisor: Dr. Francesc Piferrer Professor d’Investigació Institut de Ciències del Mar (ICM-CSIC) i ii A mis padres A Xavi iii iv Acknowledgements This thesis has been made possible by the support of many people who in one way or another, many times unknowingly, gave me the strength to overcome this "long and winding road". First of all, I would like to thank my supervisor, Dr. Francesc Piferrer, for his patience, guidance and wise advice throughout all this Ph.D. experience. But above all, for the trust he placed on me almost seven years ago when he offered me the opportunity to be part of his team. Thanks also for teaching me how to question always everything, for sharing with me your enthusiasm for science and for giving me the opportunity of learning from you by participating in many projects, collaborations and scientific meetings. I am also thankful to my colleagues (former and present Group of Biology of Reproduction members) for your support and encouragement throughout this journey. To the “exGBRs”, thanks for helping me with my first steps into this world. Working as an undergrad with you Dr. -
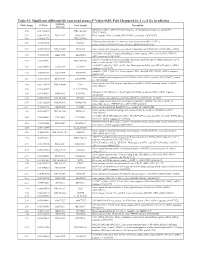
(P -Value<0.05, Fold Change≥1.4), 4 Vs. 0 Gy Irradiation
Table S1: Significant differentially expressed genes (P -Value<0.05, Fold Change≥1.4), 4 vs. 0 Gy irradiation Genbank Fold Change P -Value Gene Symbol Description Accession Q9F8M7_CARHY (Q9F8M7) DTDP-glucose 4,6-dehydratase (Fragment), partial (9%) 6.70 0.017399678 THC2699065 [THC2719287] 5.53 0.003379195 BC013657 BC013657 Homo sapiens cDNA clone IMAGE:4152983, partial cds. [BC013657] 5.10 0.024641735 THC2750781 Ciliary dynein heavy chain 5 (Axonemal beta dynein heavy chain 5) (HL1). 4.07 0.04353262 DNAH5 [Source:Uniprot/SWISSPROT;Acc:Q8TE73] [ENST00000382416] 3.81 0.002855909 NM_145263 SPATA18 Homo sapiens spermatogenesis associated 18 homolog (rat) (SPATA18), mRNA [NM_145263] AA418814 zw01a02.s1 Soares_NhHMPu_S1 Homo sapiens cDNA clone IMAGE:767978 3', 3.69 0.03203913 AA418814 AA418814 mRNA sequence [AA418814] AL356953 leucine-rich repeat-containing G protein-coupled receptor 6 {Homo sapiens} (exp=0; 3.63 0.0277936 THC2705989 wgp=1; cg=0), partial (4%) [THC2752981] AA484677 ne64a07.s1 NCI_CGAP_Alv1 Homo sapiens cDNA clone IMAGE:909012, mRNA 3.63 0.027098073 AA484677 AA484677 sequence [AA484677] oe06h09.s1 NCI_CGAP_Ov2 Homo sapiens cDNA clone IMAGE:1385153, mRNA sequence 3.48 0.04468495 AA837799 AA837799 [AA837799] Homo sapiens hypothetical protein LOC340109, mRNA (cDNA clone IMAGE:5578073), partial 3.27 0.031178378 BC039509 LOC643401 cds. [BC039509] Homo sapiens Fas (TNF receptor superfamily, member 6) (FAS), transcript variant 1, mRNA 3.24 0.022156298 NM_000043 FAS [NM_000043] 3.20 0.021043295 A_32_P125056 BF803942 CM2-CI0135-021100-477-g08 CI0135 Homo sapiens cDNA, mRNA sequence 3.04 0.043389246 BF803942 BF803942 [BF803942] 3.03 0.002430239 NM_015920 RPS27L Homo sapiens ribosomal protein S27-like (RPS27L), mRNA [NM_015920] Homo sapiens tumor necrosis factor receptor superfamily, member 10c, decoy without an 2.98 0.021202829 NM_003841 TNFRSF10C intracellular domain (TNFRSF10C), mRNA [NM_003841] 2.97 0.03243901 AB002384 C6orf32 Homo sapiens mRNA for KIAA0386 gene, partial cds. -

Human Social Genomics in the Multi-Ethnic Study of Atherosclerosis
Getting “Under the Skin”: Human Social Genomics in the Multi-Ethnic Study of Atherosclerosis by Kristen Monét Brown A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Epidemiological Science) in the University of Michigan 2017 Doctoral Committee: Professor Ana V. Diez-Roux, Co-Chair, Drexel University Professor Sharon R. Kardia, Co-Chair Professor Bhramar Mukherjee Assistant Professor Belinda Needham Assistant Professor Jennifer A. Smith © Kristen Monét Brown, 2017 [email protected] ORCID iD: 0000-0002-9955-0568 Dedication I dedicate this dissertation to my grandmother, Gertrude Delores Hampton. Nanny, no one wanted to see me become “Dr. Brown” more than you. I know that you are standing over the bannister of heaven smiling and beaming with pride. I love you more than my words could ever fully express. ii Acknowledgements First, I give honor to God, who is the head of my life. Truly, without Him, none of this would be possible. Countless times throughout this doctoral journey I have relied my favorite scripture, “And we know that all things work together for good, to them that love God, to them who are called according to His purpose (Romans 8:28).” Secondly, I acknowledge my parents, James and Marilyn Brown. From an early age, you two instilled in me the value of education and have been my biggest cheerleaders throughout my entire life. I thank you for your unconditional love, encouragement, sacrifices, and support. I would not be here today without you. I truly thank God that out of the all of the people in the world that He could have chosen to be my parents, that He chose the two of you. -

Journal Pre-Proof
Journal Pre-proof A novel homozygous missense variant in MATN3 causes spondylo-epimetaphyseal dysplasia Matrilin 3 type in a consanguineous family Samina Yasin, Saima Mustafa, Arzoo Ayesha, Muhammad Latif, Mubashir Hassan, Muhammad Faisal, Outi Makitie, Furhan Iqbal, Sadaf Naz PII: S1769-7212(20)30038-0 DOI: https://doi.org/10.1016/j.ejmg.2020.103958 Reference: EJMG 103958 To appear in: European Journal of Medical Genetics Received Date: 22 January 2020 Revised Date: 11 May 2020 Accepted Date: 17 May 2020 Please cite this article as: S. Yasin, S. Mustafa, A. Ayesha, M. Latif, M. Hassan, M. Faisal, O. Makitie, F. Iqbal, S. Naz, A novel homozygous missense variant in MATN3 causes spondylo-epimetaphyseal dysplasia Matrilin 3 type in a consanguineous family, European Journal of Medical Genetics (2020), doi: https://doi.org/10.1016/j.ejmg.2020.103958. This is a PDF file of an article that has undergone enhancements after acceptance, such as the addition of a cover page and metadata, and formatting for readability, but it is not yet the definitive version of record. This version will undergo additional copyediting, typesetting and review before it is published in its final form, but we are providing this version to give early visibility of the article. Please note that, during the production process, errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain. © 2020 Published by Elsevier Masson SAS. Authorship statement Samina Yasin: Methodology, Investigation, Formal analysis, Data curation, -

SNP Co-Association and Network Analyses Identify E2F3, KDM5A And
www.nature.com/scientificreports OPEN SNP co-association and network analyses identify E2F3, KDM5A and BACH2 as key regulators of the Received: 21 March 2017 Accepted: 27 November 2017 bovine milk fatty acid profle Published: xx xx xxxx Sara Pegolo 1, Christos Dadousis1, Núria Mach2, Yuliaxis Ramayo-Caldas2,3, Marcello Mele4, Giuseppe Conte4, Stefano Schiavon1, Giovanni Bittante1 & Alessio Cecchinato 1 The fatty acid (FA) profle has a considerable impact on the nutritional and technological quality of milk and dairy products. The molecular mechanism underlying the regulation of fat metabolism in bovine mammary gland have been not completely elucidated. We conducted genome-wide association studies (GWAS) across 65 milk FAs and fat percentage in 1,152 Brown Swiss cows. In total, we identifed 175 signifcant single nucleotide polymorphism (SNPs) spanning all chromosomes. Pathway analyses revealed that 12:0 was associated with the greatest number of overrepresented categories/pathways (e.g. mitogen-activated protein kinase (MAPK) activity and protein phosphorylation), suggesting that it might play an important biological role in controlling milk fat composition. An Associated Weight Matrix approach based on SNP co-associations predicted a network of 791 genes related to the milk FA profle, which were involved in several connected molecular pathways (e.g., MAPK, lipid metabolism and hormone signalling) and undetectable through standard GWAS. Analysis of transcription factors and their putative target genes within the network identifed BACH2, E2F3 and KDM5A as key regulators of milk FA metabolism. These fndings contribute to increasing knowledge of FA metabolism and mammary gland functionality in dairy cows and may be useful in developing targeted breeding practices to improve milk quality. -

Content Based Search in Gene Expression Databases and a Meta-Analysis of Host Responses to Infection
Content Based Search in Gene Expression Databases and a Meta-analysis of Host Responses to Infection A Thesis Submitted to the Faculty of Drexel University by Francis X. Bell in partial fulfillment of the requirements for the degree of Doctor of Philosophy November 2015 c Copyright 2015 Francis X. Bell. All Rights Reserved. ii Acknowledgments I would like to acknowledge and thank my advisor, Dr. Ahmet Sacan. Without his advice, support, and patience I would not have been able to accomplish all that I have. I would also like to thank my committee members and the Biomed Faculty that have guided me. I would like to give a special thanks for the members of the bioinformatics lab, in particular the members of the Sacan lab: Rehman Qureshi, Daisy Heng Yang, April Chunyu Zhao, and Yiqian Zhou. Thank you for creating a pleasant and friendly environment in the lab. I give the members of my family my sincerest gratitude for all that they have done for me. I cannot begin to repay my parents for their sacrifices. I am eternally grateful for everything they have done. The support of my sisters and their encouragement gave me the strength to persevere to the end. iii Table of Contents LIST OF TABLES.......................................................................... vii LIST OF FIGURES ........................................................................ xiv ABSTRACT ................................................................................ xvii 1. A BRIEF INTRODUCTION TO GENE EXPRESSION............................. 1 1.1 Central Dogma of Molecular Biology........................................... 1 1.1.1 Basic Transfers .......................................................... 1 1.1.2 Uncommon Transfers ................................................... 3 1.2 Gene Expression ................................................................. 4 1.2.1 Estimating Gene Expression ............................................ 4 1.2.2 DNA Microarrays ...................................................... -

Title: a Yeast Phenomic Model for the Influence of Warburg Metabolism on Genetic
bioRxiv preprint doi: https://doi.org/10.1101/517490; this version posted January 15, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC 4.0 International license. 1 Title Page: 2 3 Title: A yeast phenomic model for the influence of Warburg metabolism on genetic 4 buffering of doxorubicin 5 6 Authors: Sean M. Santos1 and John L. Hartman IV1 7 1. University of Alabama at Birmingham, Department of Genetics, Birmingham, AL 8 Email: [email protected], [email protected] 9 Corresponding author: [email protected] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 1 bioRxiv preprint doi: https://doi.org/10.1101/517490; this version posted January 15, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC 4.0 International license. 26 Abstract: 27 Background: 28 Saccharomyces cerevisiae represses respiration in the presence of adequate glucose, 29 mimicking the Warburg effect, termed aerobic glycolysis. We conducted yeast phenomic 30 experiments to characterize differential doxorubicin-gene interaction, in the context of 31 respiration vs. glycolysis. The resulting systems level biology about doxorubicin 32 cytotoxicity, including the influence of the Warburg effect, was integrated with cancer 33 pharmacogenomics data to identify potentially causal correlations between differential 34 gene expression and anti-cancer efficacy. -

Anti-OSBP1 Antibody Catalog # ABO11254
10320 Camino Santa Fe, Suite G San Diego, CA 92121 Tel: 858.875.1900 Fax: 858.622.0609 Anti-OSBP1 Antibody Catalog # ABO11254 Specification Anti-OSBP1 Antibody - Product Information Application WB Primary Accession P22059 Host Rabbit Reactivity Human, Mouse, Rat Clonality Polyclonal Format Lyophilized Description Rabbit IgG polyclonal antibody for Oxysterol-binding protein 1(OSBP) detection. Tested with WB in Human;Mouse;Rat. Reconstitution Add 0.2ml of distilled water will yield a concentration of 500ug/ml. Anti-OSBP1 antibody, ABO11254, Western blottingLane 1: Rat Kidney Tissue LysateLane Anti-OSBP1 Antibody - Additional Information 2: Rat Spleen Tissue LysateLane 3: Rat Lung Tissue LysateLane 4: HELA Cell LysateLane 5: A549 Cell Lysate Gene ID 5007 Other Names Anti-OSBP1 Antibody - Background Oxysterol-binding protein 1, OSBP (<a href ="http://www.genenames.org/cgi-bin/gene_ OSBP(Oxysterol-Binding Protein), also called symbol_report?hgnc_id=8503" OSBP1, is a protein that in humans is encoded target="_blank">HGNC:8503</a>), OSBP1 by the OSBP gene. Im et al.(2005) reported the structure of the full-length yeast Calculated MW oxysterol-binding-protein Osh4, a member of 89421 MW KDa the OSBP-related protein(ORP) family, at 1.5- Application Details to 1.9-angstrom resolution in complexes with Western blot, 0.1-0.5 µg/ml, Human, Rat, ergosterol, cholesterol, and 7-, 20- and Mouse<br> 25-hydroxy cholesterol. Moreira et al.(2001) refined the localization of the OSBP1 gene to Subcellular Localization chromosome 11q12.1 by radiation hybrid Cytoplasm. Golgi apparatus membrane; analysis. Wang et al.(2005) found that OSBP Peripheral membrane protein. -

Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations Fall 2010 Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress Renuka Nayak University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/edissertations Part of the Computational Biology Commons, and the Genomics Commons Recommended Citation Nayak, Renuka, "Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress" (2010). Publicly Accessible Penn Dissertations. 1559. https://repository.upenn.edu/edissertations/1559 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/edissertations/1559 For more information, please contact [email protected]. Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress Abstract Genes interact in networks to orchestrate cellular processes. Here, we used coexpression networks based on natural variation in gene expression to study the functions and interactions of human genes. We asked how these networks change in response to stress. First, we studied human coexpression networks at baseline. We constructed networks by identifying correlations in expression levels of 8.9 million gene pairs in immortalized B cells from 295 individuals comprising three independent samples. The resulting networks allowed us to infer interactions between biological processes. We used the network to predict the functions of poorly-characterized human genes, and provided some experimental support. Examining genes implicated in disease, we found that IFIH1, a diabetes susceptibility gene, interacts with YES1, which affects glucose transport. Genes predisposing to the same diseases are clustered non-randomly in the network, suggesting that the network may be used to identify candidate genes that influence disease susceptibility. -

A Meta-Analysis of the Effects of High-LET Ionizing Radiations in Human Gene Expression
Supplementary Materials A Meta-Analysis of the Effects of High-LET Ionizing Radiations in Human Gene Expression Table S1. Statistically significant DEGs (Adj. p-value < 0.01) derived from meta-analysis for samples irradiated with high doses of HZE particles, collected 6-24 h post-IR not common with any other meta- analysis group. This meta-analysis group consists of 3 DEG lists obtained from DGEA, using a total of 11 control and 11 irradiated samples [Data Series: E-MTAB-5761 and E-MTAB-5754]. Ensembl ID Gene Symbol Gene Description Up-Regulated Genes ↑ (2425) ENSG00000000938 FGR FGR proto-oncogene, Src family tyrosine kinase ENSG00000001036 FUCA2 alpha-L-fucosidase 2 ENSG00000001084 GCLC glutamate-cysteine ligase catalytic subunit ENSG00000001631 KRIT1 KRIT1 ankyrin repeat containing ENSG00000002079 MYH16 myosin heavy chain 16 pseudogene ENSG00000002587 HS3ST1 heparan sulfate-glucosamine 3-sulfotransferase 1 ENSG00000003056 M6PR mannose-6-phosphate receptor, cation dependent ENSG00000004059 ARF5 ADP ribosylation factor 5 ENSG00000004777 ARHGAP33 Rho GTPase activating protein 33 ENSG00000004799 PDK4 pyruvate dehydrogenase kinase 4 ENSG00000004848 ARX aristaless related homeobox ENSG00000005022 SLC25A5 solute carrier family 25 member 5 ENSG00000005108 THSD7A thrombospondin type 1 domain containing 7A ENSG00000005194 CIAPIN1 cytokine induced apoptosis inhibitor 1 ENSG00000005381 MPO myeloperoxidase ENSG00000005486 RHBDD2 rhomboid domain containing 2 ENSG00000005884 ITGA3 integrin subunit alpha 3 ENSG00000006016 CRLF1 cytokine receptor like -

Sheet1 Page 1 Gene Symbol Gene Description Entrez Gene ID
Sheet1 RefSeq ID ProbeSets Gene Symbol Gene Description Entrez Gene ID Sequence annotation Seed matches location(s) Ago-2 binding specific enrichment (replicate 1) Ago-2 binding specific enrichment (replicate 2) OE lysate log2 fold change (replicate 1) OE lysate log2 fold change (replicate 2) Probability NM_022823 218843_at FNDC4 Homo sapiens fibronectin type III domain containing 4 (FNDC4), mRNA. 64838 TR(1..1649)CDS(367..1071) 1523..1530 3.73 1.77 -1.91 -0.39 1 NM_003919 204688_at SGCE Homo sapiens sarcoglycan, epsilon (SGCE), transcript variant 2, mRNA. 8910 TR(1..1709)CDS(112..1425) 1495..1501 3.09 1.56 -1.02 -0.27 1 NM_006982 206837_at ALX1 Homo sapiens ALX homeobox 1 (ALX1), mRNA. 8092 TR(1..1320)CDS(5..985) 916..923 2.99 1.93 -0.19 -0.33 1 NM_019024 233642_s_at HEATR5B Homo sapiens HEAT repeat containing 5B (HEATR5B), mRNA. 54497 TR(1..6792)CDS(97..6312) 5827..5834,4309..4315 3.28 1.51 -0.92 -0.23 1 NM_018366 223431_at CNO Homo sapiens cappuccino homolog (mouse) (CNO), mRNA. 55330 TR(1..1546)CDS(96..749) 1062..1069,925..932 2.89 1.51 -1.2 -0.41 1 NM_032436 226194_at C13orf8 Homo sapiens chromosome 13 open reading frame 8 (C13orf8), mRNA. 283489 TR(1..3782)CDS(283..2721) 1756..1762,3587..3594,1725..1731,3395..3402 2.75 1.72 -1.38 -0.34 1 NM_031450 221534_at C11orf68 Homo sapiens chromosome 11 open reading frame 68 (C11orf68), mRNA. 83638 TR(1..1568)CDS(153..908) 967..973 3.07 1.35 -0.72 -0.06 1 NM_033318 225795_at,225794_s_at C22orf32 Homo sapiens chromosome 22 open reading frame 32 (C22orf32), mRNA.