Modeling and Control of an Electrically-Heated Catalyst
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bmw Alpina B6 Coupé & Convertible
BMW ALPINA B6 COUPÉ & CONVERTIBLE MANUFACTURER OF EXCLUSIVE AUTOMOBILES GRAND TOURERS... ...have a long tradition at ALPINA. It began with the legendary BMW ALPINA 3.0 CSL lightweight Coupé in the early 1970s, a car that caused a great furore, both as a race car and a road car. It was with this car that ALPINA won the European Touring Car Championship in 1973 and 1977. Since it débuted in 1978, friends of BMW 6 Series Coupés have awarded the 300 horsepower BMW ALPINA B7 Turbo Coupé – 330hp/512Nm-strong in the S-Version – cult status, making it a desired collector’s car. The elegant BMW 8 Series was the basis for the BMW ALPINA B12 5.7 Coupé, noticeable at a glance due to its carbon-fibre bonnet with NACA ducts. And with its top speed of 186mph, ALPINA was a leader in this regard, as well The maxim then as now was to offer performance on the level of exotic sports cars, coupled with high quality and the everyday “useability” only available from a volume manufacturer – such as BMW – on whose excellent basis we deliver GRAND TOURERS... FFIRSTI R S T CCLASS...L A S S . The BMW ALPINA B6 Coupé, yet another true Grand Tourisme, is a long-distance automobile par excellence. It is amply powered by 500 horsepower and 700Nm. The V8’s beguiling sound and opulent torque beg one to drive in a completely relaxed manner, any and all red-line orgies far afield, with more torque at tickover than most cars have in total. -

Mar 2021 2015
VOL 8 ISSUE 1 Jan – Mar 2021 2015 © 2021 BMW Car Club of America E31 Chapter 1 VOL 8 ISSUE 1 Editor: Roger Wray Jan – Mar 2021 2020 E31 Chapter Table BMW Car Club of America of Contents ______________________________________________________________ __________________________________________________________________ • President’s Perspective Chapter Officers (please call between 7:30-10pm) 2015 President [email protected] • Special Thank You to Gault BMW Autosport Henry Christoff (BC, Canada) 604-787-7706 • Election Announcement – Vice President and Vice President [email protected] Treasurer Alec Cartio (California) 818-395-5765 Secretary [email protected] • SoCalEights Wrenchfest Kirsti Christoff (BC, Canada) 604-787-7706 • A BMW 850Ci That’s Actually an E63 M6 Treasurer [email protected] • The 8 is Back! Jack Woods (Massachusetts) 978-532-0266 Brands Manager [email protected] • Tech Tip: How to replace the Pilot Bearing, Brian Diffenbacher (Arizona) 949-636-0118 and eat your tools too! National Events Coordinator [email protected] Michael Barrett (Pennsylvania) 717-514-4003 • Leatherique and Colourlock Products – 2021 Update Other • NEW 2021 Chapter T-Shirts Webmaster [email protected] Bob Bennett (Florida) 813-787-8837 • The E31 Chapter Apparel Store Newsletter Editor [email protected] • The Tail Lights Roger Wray (Florida) 352-223-2932 Membership Chairperson [email protected] Kirsti Christoff (BC, Canada) 604-787-7706 2021 Upcoming Events Also Check group contacts for the latest information Regional Facilitators _____________________________________________________________ Pacific Northwest Tom “Wuffer” Carter 604-530-6609 Southeast US Roger Wray 352-223-2932 BC8s Breakfast Club Cars & Coffee, April 11 Tim Hortons 2711 192nd Street, Surrey BC Liaison: International E31 Groups and Enthusiasts [email protected] Roger Wray [email protected] 352-223-2932 BC 8’s WrenchFest, May 15 BMW CCA E31 is a non-profit South Carolina Corporation. -
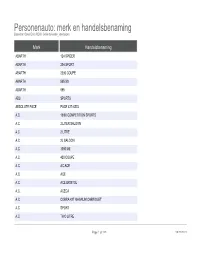
Merk En Handelsbenaming Based on Open Data RDW: Gekentekende Voertuigen
Personenauto: merk en handelsbenaming Based on Open Data RDW: Gekentekende_voertuigen Merk Handelsbenaming ABARTH 124 SPIDER ABARTH 204 SPORT ABARTH 2200 COUPE ABARTH 595 SS ABARTH 695 ABS SPORTS ABSOLUTE PACE PACE 427-4SSL A.C. 16/80 COMPETITION SPORTS A.C. 2.LITER SALOON A.C. 2 LITRE A.C. 2L SALOON A.C. 3000 ME A.C. 428 COUPE A.C. AC ACE A.C. ACE A.C. ACE BRISTOL A.C. ACECA A.C. COBRA 427 MAGNUM CABRIOLET A.C. SPORT A.C. TWO LITRE Page 1 of 239 09/29/2021 Personenauto: merk en handelsbenaming Based on Open Data RDW: Gekentekende_voertuigen A.C. TWO-SEATER DHC A.C. AUTOKRAFT AC.MK IV A.C. AUTOKRAFT COBRA MK4 A.C. AUTOKRAFT COBRA MK IV ACCUBUILT CHS ACHLEITNER PIAS 4X4-35C18V ACHLEITNER PIAS 4X4 50C18 A.C.L. 1 A A.C.L. 1A RODEO A.C.L. 1 ARODEO 4 A.C.L. 2B RODEO 6 A.C.L. RODEO A.C.L. RODEO 6 ACROSS AERO ACROSS EXCAPE ACURA 1.6 EL ACURA 4D SDN ACURA ACURA RDX TURBO ACURA ACURA RSX S ACURA ACURA TL ACURA INTEGRA ACURA INTEGRA LS Page 2 of 239 09/29/2021 Personenauto: merk en handelsbenaming Based on Open Data RDW: Gekentekende_voertuigen ACURA LEGEND ACURA MDX ACURA NSX ACURA NSX 3.0 ACURA NSX 3.0 V6 ACURA NSX-T ACURA RDX ACURA RDX-T ACURA RL ACURA RSX ACURA RSX TYPE S ACURA TL 2.5 ACURA TSX ACURA ZDX ADLER 2EV ADLER JUNIOR ADLER PRIMUS ADLER PRUMP JUNIOR ADLER TRUMPF ADLER TRUMPF 1,7 AV ADLER TRUMPF (1,7 EV) Page 3 of 239 09/29/2021 Personenauto: merk en handelsbenaming Based on Open Data RDW: Gekentekende_voertuigen ADLER TRUMPF JR 1E ADLER TRUMPF JUNIOR ADLER TRUMPF-JUNIOR ADLER TRUMPH JUNIOR 1 E ADRIA 35 HEAVY ADRIA 35 LIGHT ADRIA 43 -

Bmw Alpina B7
Table of Contents BMW ALPINA B7 Subject Page Introduction . .3 Technical Data . .4 ALPINA History . .6 Body . .14 Exterior . .14 Spoilers . .15 Front . .15 Rear . .15 The Read Lid . .16 Wheels . .16 Wheel Locks . .17 Interior . .18 Steering Wheel . .18 Electronics . .19 Drivetrain . .20 Engine . .20 Supercharger . .21 Design . .22 Clutch . .24 Service . .24 Boost Regulator / Secondary Throttle . .25 Pressure Sensor . .26 Cooling Module . .26 Chassis . .27 Suspension . .27 Brakes . .27 Differential . .27 Initial Print Date: 01/07 Revision Date: BMW ALPINA B7 Model: E65 Production: from 11/2006 (2007 MY) After completion of this module you will be able to: • Identify a BMW ALPINA B7. • Explain the differences between a conventional E65 and a B7. • Know what additional service is required on the supercharger. 2 BMW ALPINA B7 Introduction Committed to developing the best performing vehicles in the luxury market, BMW with ALPINA has created a special high performance version of BMW’s 7 Series luxury sedan. The 2006 BMW ALPINA B7 brings together the luxury, pioneering design, and advanced technology of the 7 Series Sedan with the scintillating performance of a supercharged, 500hp V-8 engine. To power the BMW ALPINA B7, ALPINA specially developed a higher-performance version of BMW’s 4.4-liter, 90-degree V-8 engine and mated it to a 6-speed automatic transmission featuring steering wheel mounted shift controls. The motor produces 500 horsepower at 5,500 rpm along with maximum torque of 516 lbs.-ft. at 4,250 rpm, and propels the B7 from 0-60 mph in a mere 4.8 seconds. -

Jun 2020 2015
VOL 7 ISSUE 2 Apr – Jun 2020 2015 © 2020 BMW Car Club of America E31 Chapter 1 VOL 7 ISSUE 2 Editor: Roger Wray Apr - Jun 2020 E31 Chapter Table BMW Car Club of America of Contents _______________________________ _______________________________ ___________________________________________________________ 2015 ___ ____ • From the Driver's Seat Chapter Officers (please call between 7:30-10pm) President [email protected] • Announcement: 2020 E31 Chapter Photo Steffen Staiger (Texas) 214-417-0606 Contest Vice President [email protected] • Member Spotlight – Mart Jamma Alec Cartio (California) 818-395-5765 Secretary [email protected] • Why did I buy my 840 Ci Henry Christoff (Canada) 604-787-7706 • SoCalEights Farewell to Ron & Sonjia Powell Treasurer [email protected] • BC 8s May Wrenchfest at Wuffer’s Garage & Jack Woods (Massachusetts) 978-532-0266 Brands Manager [email protected] Spa Brian Diffenbacher (Arizona) 949-636-0118 • BC 8’s Spring Outing – with Social Distancing National Events Coordinator [email protected] Michael Barrett (Pennsylvania) 717-514-4003 • The Road to a Dream Car • Electronic Dampening Control in Alpina B12 Other Coupes Webmaster [email protected] Bob Bennett (Florida) 813-787-8837 • International News – E31 NEWS is now the Newsletter Editor [email protected] International Voice for E31 Clubs Roger Wray (Florida) 352-223-2932 • Membership Chairperson [email protected] German 8 Owners SONAX Tech Session Henry Christoff (Canada) 604-787-7706 • New Product - Front License Plate Filler • Hagerty Vehicle Valuation Report Update Regional Facilitators Pacific Northwest Tom “Wuffer” Carter 604-530-6609 2020 – BMW 850 CSi Southeast US Roger Wray 352-223-2932 • Tech Corner - Making Error- Free LED License- Plate Lights BMW CCA E31 is a non-profit South Carolina Corporation. -

ECOLOGIC OIL FILTERS Pre-Code: 10-ECO
JAPANPARTS GROUP 01 05 - 2018 ECOLOGIC OIL FILTERS Pre-code: 10-ECO www.japanpartsgroup.com ikone grige vettoriali per distributori.indd 1 10/08/17 16:44 Senza titolo-1 1 29/06/17 12:17 loghi prodotto japanparts group con ®.indd 2 23/03/17 10:31 10-ECO001 5411800009 10-ECO002 51055040098 MAN F 90 19.342 F,19.342 FL,19.342 FLL MAN F 2000 19.293 FAC MAN F 90 19.342 FA MAN F 2000 19.293 FAK MAN F 90 19.342 FAK MAN F 2000 19.293 FAS MAN F 90 19.342 FAS MAN F 2000 19.293 FC,19.293 FLC,19.293 FLLC MAN F 90 19.342 FK MAN F 2000 19.293 FK,19.293 FLK MAN F 90 19.342 FS,19.342 FLS,19.342 FLLS MAN F 2000 19.293 FS,19.293 FLS,19.293 FLLS MERCEDES-BENZ ACTROS 1831 AK MAN F 2000 19.314 FC,19.314 FLC,19.314 FLLC MERCEDES-BENZ ACTROS 1831 K MAN F 2000 19.314 FK,19.314 FLK 10-ECO003 166.180.00.09 10-ECO004 11421432097 MERCEDES-BENZ CLASSE A (W168) A 140 BMW 3 (E36) 316 i (168.031, 168.131) BMW 3 (E36) 318 i MERCEDES-BENZ CLASSE A (W168) A 160 BMW 3 (E36) 318 is (168.033, 168.133) BMW 3 (E36) 320 i MERCEDES-BENZ CLASSE A (W168) A 160 CDI BMW 3 (E36) 323 i 2.5 (168.007) BMW 3 (E36) 325 td MERCEDES-BENZ CLASSE A (W168) A 190 BMW 3 (E36) 325 tds (168.032, 168.132) BMW 3 (E36) 328 i 10-ECO005 05650319 10-ECO006 05102904AA OPEL ASTRA G 2 volumi /Coda spiovente (F48_, CHRYSLER CROSSFIRE 3.2 F08_) 2.0 DI CHRYSLER CROSSFIRE Roadster 3.2 OPEL ASTRA G 2 volumi /Coda spiovente (F48_, CHRYSLER CROSSFIRE Roadster SRT-6 F08_) 2.0 DTI 16V CHRYSLER CROSSFIRE SRT-6 OPEL ASTRA G 2 volumi /Coda spiovente (F48_, MERCEDES-BENZ CLASSE C (W202) C 240 F08_) 2.2 DTI (202.026) -

DEPARTMENT of TRANSPORTATION National
This document is scheduled to be published in the Federal Register on 09/25/2013 and available online at http://federalregister.gov/a/2013-23358, and on FDsys.gov DEPARTMENT OF TRANSPORTATION National Highway Traffic Safety Administration [Docket No. NHTSA-2013-0064; Notice 1] Notice of Receipt of Petition for Decision that Nonconforming 1988-1996 Alpina B10 Passenger Cars Are Eligible for Importation AGENCY: National Highway Traffic Safety Administration, DOT ACTION: Receipt of petition. SUMMARY: This document announces receipt by the National Highway Traffic Safety Administration (NHTSA) of a petition for a decision that nonconforming 1988-1996 Alpina B10 passenger cars that were not originally manufactured to comply with all applicable Federal Motor Vehicle Safety Standards (FMVSS), are eligible for importation into the United States because they have safety features that comply with, or are capable of being altered to comply with, all such standards. DATE: [INSERT DATE 30 DAYS AFTER DATE OF PUBLICATION IN THE FEDERAL REGISTER] ADDRESSES: Comments should refer to the docket and notice numbers above and be submitted by any of the following methods: • Federal eRulemaking Portal: Go to http://www.regulations.gov. Follow the online instructions for submitting comments. 2 • Mail: Send comments by mail addressed to: U.S. Department of Transportation, 1200 New Jersey Avenue S.E., West Building Ground Floor, Room W12-140, Washington, D.C. 20590-0001 • Hand Delivery: Deliver comments by hand to: West Building Ground Floor, Room W12-140, 1200 New Jersey Avenue S.E., between 9 a.m. and 5 p.m. ET, Monday through Friday, except Federal holidays. -

Gran Turismo 5 As of Today Sony Has Announced the Full Gran Turismo 5
Gran Turismo 5 As of today Sony has announced the full Gran Turismo 5 car list. It consists of 10000 cars. At launch it will only have 340 cars while the others will be developed in the future. Polyphony Digital will also develop cars for individual clients. That means in the future we could have any car put into the game for a special price. Of course the damage model will be not present in GT5. Below we are attaching the nearly official car list of GT5. Be ready for more info in the close future! 1G RACING/ROSSION AUTOMOTIVE Rossion Q1 Supercar '08 9FF FAHRZEUGTECHNIK 9ff [Cayman S] CCR42 {4.1L, 420hp} '06 9ff [996] 9fT1 Turbo '03 9ff [996] 9f V400 '04 9ff [997] Aero '05 9ff [997] Carrera Turbo Stage I '06 9ff [997] Carrera Turbo Stage II '06 9ff [977] Carrera Turbo Stage III '06 9ff [997] Carrera Turbo Cabrio Stage III '06 9ff [997] Cabrio [650hp] '06 9ff [Carrera GT] =unnamed= '06 9ff [997] TCR84 '07 9ff [997 Turbo] TRC 91 '07 A:LEVEL A:Level BIG '03 A:Level Volga V12 Coupe '03 A:Level Volga V8 Convertible '06 A:Level Impression '05 A&L RACING A&L Racing S2000 '04 AB FLUG Toyota Supra 80 ' Nissan Fairlady Z32 '89 Nissan Skyline GTR R32 ' Nissan Skyline GTR R33 ' Nissan Skyline GTR R34 ' Toyota Supra S900 '01 Toyota Supra 70 ' Mazda RX7 [FD3S] ' Toyota Aristo 161 ' Mazda RX8 ' Toyota Supra Tamura Veil Black S900 ' Toyota Supra Zefi:r MA04S ' ABARTH Abarth Simca ' Abarth Stola Monotipo Concept '98 Abarth 1000 Bialbero ' Abarth OT850 ' Abarth OT1000 ' Abarth OTR1000 ' Abarth OT1300/124 ' Abarth OT1600 ' Abarth OT2000 ' ABD RACING ABD -

Complete List of Classic BMW Alpina Models for Collectors
Complete list of classic BMW Alpina models for collectors: 3 Series 5 Series BMW Alpina C1 2.3 E21 323i 2dr apr 80 - jul 83 BMW Alpina B7 Turbo E12 528i dec 78 - feb 82 BMW Alpina B6 2.8 E21 323i 2dr nov 78 - aug 81 BMW Alpina B7 S Turbo E12 528i nov 81 - may 82 BMW Alpina B6 2.8 E21 323i 2dr sep 81 - jan 83 BMW Alpina B9 3.5 E28 528i nov 81 - aug 83 BMW Alpina C1 2.3 / 1 E30 323i 2dr aug 83 - nov 85 BMW Alpina B9 3.5 / 1 E28 528i jan 83 - dec 85 BMW Alpina C1 2.5 E30 325i 2dr, 4dr, Conv sep 86 - jul 87 BMW Alpina B10 3.5 E28 535i jul 85 - dec 87 BMW Alpina C2 2.5 E30 325i 2dr, 4dr, apr 85 - nov 86 BMW Alpina B7 Turbo / 1 E28 535i aug 86 - dec 87 BMW Alpina C2 2.7 E30 325i 2dr, 4dr, Conv & AWD feb 86 - jul 87 BMW Alpina B10 3.5 / 1 E34 535i apr 88 - dec 92 BMW Alpina C2 2.7 E30 325i 2dr, 4dr, Conv & AWD mar 87 - jul 87 BMW Alpina B10 BiTurbo E34 535i aug 89 - mar 94 BMW Alpina B3 2.7 E30 325i All Shapes aug 87 - jun 92 BMW Alpina B10 3.0 AWD E34 525ix Saloon, Touring oct 93 - may 96 BMW Alpina B6 2.8 / 1 E30 323i, 325i 2dr, 4dr, mar 84 - jul 86 BMW Alpina B10 4.0 E34 540i Saloon, Touring apr 93 - aug 95 BMW Alpina B6 3.5 E30 323i, 325i 2dr, 4dr, nov 85 - jul 87 BMW Alpina B10 4.6 E34 540i Saloon, Touring mar 94 - apr 96 BMW Alpina B6 3.5 E30 325i 2dr, 4dr, aug 86 - jul 87 BMW Alpina B10 3.2 E39 528i Saloon, Touring aug 97 - dec 98 BMW Alpina B6 3.5 E30 325i 2dr, 4dr, nov 87 - dec 90 BMW Alpina B10 3.3 E39 528i Saloon, Touring feb 99 - oct 03 BMW Alpina B6 3.5 S E30 M3 2dr nov 87 - dec 90 BMW Alpina B10 V8 E39 540i Saloon, Touring jan -

The Alpina Book
2 KAPITEL DEUTSCH 3 2 KAPITEL ENGLISCH 3 Die große Alpina-Familie 2014 auf dem Buchloer Werksgelände versammelt. 4 KAPITEL DEUTSCH 5 The big Alpina family gathering at the Buchloe factory premises in 2014. 4 KAPITEL ENGLISCH 5 LIEBE LESERINNEN UND LESER Prof. Dr.-Ing. Dr. h.c. Dr.-Ing. E.h. Joachim Milberg Dr.-Ing. Dr.-Ing. E.h. Norbert Reithofer Aufsichtsratsvorsitzender der BMW AG Vorstandsvorsitzender der BMW AG 2004–2015 2006–2015 Das Jahr 2016 markiert einen wichtigen Alpina – für viele Automobil-Enthusiasten Meilenstein in der Geschichte von BMW. ist dieser Name ein Mythos. Begonnen hat Dann wird das Unternehmen 100 Jahre alt. Burkard Bovensiepen am 1. Januar 1965 mit Ein anderes bayerisches Unternehmen aus acht Mitarbeitern als ebenso kompetenter der Automobilindustrie begeht bereits ein wie leidenschaftlicher Fahrzeugtuner, dessen Jahr zuvor – 2015 – sein großes Jubiläum: Produkte die volle Werksgarantie erhielten. Alpina wird 50 Jahre alt. Genauso lange wie Inzwischen ist Alpina zu einem selbstständi- Alpina existiert die Zusammenarbeit beider gen Motorenentwickler und eingetragenen Automobilhersteller. Seit der Gründung Autohersteller gereift. Hochwertige Premi- ergänzt Alpina mit exklusiven und souverä- umfahrzeuge werden für einen exklusiven nen »Meisterwerken« die Produktpalette von Kreis besonders anspruchsvoller Kunden BMW. Diese lange Zeit der Kooperation veredelt und individualisiert. Nur die Rolle zeigt, wie stabil die Partnerschaft ist. eines Konkurrenten von BMW gehört in den Bereich der Mythologie. Alpina und die BMW Group teilen die Leidenschaft für Premiumautomobile. Die Denn: BMW und Alpina pflegen eine Passion von Burkard Bovensiepen liegt partnerschaftliche Beziehung – und das seit darin, die Leistung ausgewählter BMW- einem halben Jahrhundert. Die Verbindung Automobile zu steigern und den Fahrzeugen der BMW Group, die sich seit der Jahrtau- einen sehr eigenständigen Charakter mit- sendwende ausschließlich auf die Premium- zugeben. -

Alpina B12 5,7I E38 '96 Sold
Alpina B12 5,7i e38 '96 Sold Vehicle Description Alpina B12 5,7 – one of the most powerful versions of the classic BMW 7 Series e38 – original modified by the famous german BMW tuner. It is one of only 202 units manufactured by Alpina – this Specifications particular vehicle holds number 30. The car is fully original – it has all of the features of the unique Alpina B12. V12 engine is full of Make Alpina power and works amizngly smoothly on low RPMs – Alpina B12 is a Model B12 5,7i car with unrepeatable character. Japanese service records, manuals, japanese export certificate proving original kilometers: Production date 1996 just 142.000! More information about this car via phone or e-mail Kilometer 142 000 km +48 606 502 793; +48 888 037 000; [email protected] Transmission Automatic IMPORTANT: Collectible vehicles from Japan are left-hand drive transmission and use metric units – you can drive them just like any european car!!! Full books documentation since first registration. Why Drive RWD should you buy a car imported from Japan? Here’s why: First of all Fuel Type Petrol for Japanese people owning a car with a steering wheel on a Cubic Capacity 5646 cm3 “wrong” side is a symptom of luxury and prestige. Secondly – they Power (HP) 387 just love their cars and are pedantic about keeping them in a mint condition. Thirdly – driving a left-hand drive… Colour niebieski/blue Wyposażenie dodatkowe ABS, Central Locking, Keyless Entry, Rain Sensor, Parking Sensors, Electric Seat Adjustment, Electric Side Mirrors, Electric Windows, Alloy Wheels, Air Conditioning, On Board Computer, Traction Control, Navigation System, CD Player, Full Leather, Electric Heated Seats, Airbags, Xenon Headlights, Sunroof, Fog Lamps, Cruise Control, Multifunction Steering Wheel, Power Assisted Steering Copyright 2021 © KIMBEX - www.kimbex.pl Page 1 z 1. -

The New Bmw Alpina B6 S Coupé and Cabrio Design Meets Performance
THE NEW BMW ALPINA B6 S COUPÉ AND CABRIO DESIGN MEETS PERFORMANCE MANUFACTURER OF EXCLUSIVE AUTOMOBILES 88 04 212 - 0907 Printed in Germany 0.25 © ALPINA 88 04 212 - 0907 Printed in Germany 0.25 © Grand Tourers have a long tradition at ALPINA. It began with the legendary BMW ALPINA 3,0 CSL lightweight Coupé in the early 1970s, a car that caused a great furore, both as a race car and as a street car. It was with this car that ALPINA won the European Touring Car Championship in 1973 and 1977. Since it débuted in 1978, friends of BMW 6 Series Coupés have awarded the 300 bhp BMW ALPINA B7 Turbo Coupé (with 330 bhp / 512 Nm in the S-Version) cult status, making it a desired collector’s car. The elegant BMW 8 Series was the basis for the BMW ALPINA B12 5,7 Coupé, identifiable at a glance thanks to its carbon-fibre bonnet with NACA ducts. This is how and where Buchloe’s newest creation, the BMW ALPINA B6 S, ties in. The eye immediately focuses on the new bonnet. Gently rising from the bonnet’s front edge to the windscreen, the elevated centre channel visually awards the front and indeed the entire automobile, added length. Halfway up, two vertical air outlets are harmoniously integrated, air exiting precisely from under the bonnet through stainless steel latticework – much like in racing. The flowing lines of the B6 S bonnet impart both power and elegance. In technical terms, the lightweight (just under 10kg) composite construction is a tour de force.