Skill, Luck and Hot Hands on the PGA Tour
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Media Guide.Pdf
2018 wichita open Results POS PLAYER Total R1 R2 R3 R4 STROKES OFFICIAL MONEY 1 Brady Schnell -14 72 64 64 66 266 $112,500 T2 Brandon Hagy -14 71 65 67 63 266 $55,000 T2 Scott Pinckney -14 67 64 67 68 266 $55,000 T4 Wes Roach -12 70 67 65 66 268 $25,833 T4 Justin Hueber -12 70 68 65 65 268 $25,833 T4 Sebastian Cappelen -12 65 68 66 69 268 $25,833 7 Cameron Champ -11 71 66 65 67 269 $20,938 T8 Carlos Ortiz -10 71 66 69 64 270 $17,500 T8 Kyoung-Hoon Lee -10 71 69 66 64 270 $17,500 T8 Ben Kohles -10 65 69 70 66 270 $17,500 T8 Joseph Bramlett -10 72 64 68 66 270 $17,500 T12 Kyle Reifers -9 73 68 68 62 271 $12,656 T12 Patrick Newcomb -9 69 71 65 66 271 $12,656 T12 Wyndham Clark -9 76 65 63 67 271 $12,656 T12 Mark Blakefield -9 71 65 67 68 271 $12,656 T16 Ryan Yip -8 71 66 70 65 272 $9,375 T16 Tim Wilkinson -8 71 68 65 68 272 $9,375 T16 Chris Baker -8 70 69 65 68 272 $9,375 T16 Bryan Bigley -8 73 66 65 68 272 $9,375 T16 Chris Thompson -8 70 64 69 69 272 $9,375 T21 Seth Reeves -7 69 71 67 66 273 $6,750 T21 Brian Richey -7 72 64 72 65 273 $6,750 T21 Ben Crancer -7 69 69 68 67 273 $6,750 T21 Jose de Rodriguez -7 66 69 69 69 273 $6,750 T25 Tag Ridings -6 73 67 68 66 274 $4,753 T25 Rico Hoey -6 69 70 69 66 274 $4,753 T25 Jin Park -6 69 68 71 66 274 $4,753 T25 Steven Alker -6 74 67 66 67 274 $4,753 T25 Ryan Brehm -6 73 65 68 68 274 $4,753 T25 Billy Kennerly -6 70 69 66 69 274 $4,753 T25 Vince Covello -6 72 69 63 70 274 $4,753 3 Tournament Winners 1990 Tom Lehman 66-69-67 202 (-14) $20,000 Reflection Ridge GC 1991 Eric Hoos 61-66-72 199 (-17) $25,000 -

THE PLAYERS Championship 2019 (20Th of 46 Events in the 2018-19 PGA TOUR Season) Ponte Vedra Beach, Florida March 14-17, 2019 Pu
THE PLAYERS Championship 2019 (20th of 46 events in the 2018-19 PGA TOUR Season) Ponte Vedra Beach, Florida March 14-17, 2019 Purse: $12,500,000 ($2,250,000) THE PLAYERS Stadium Course at TPC Sawgrass Par/Yards: 36-36—72/7,189 Second-Round Notes – Friday, March 15, 2019 Weather: Partly cloudy. High of 80. Wind S 10-18 mph. 36-Hole Cut: 80 players at 1-under 143 from a field of 141 professionals. Second-Round Leaderboard Tommy Fleetwood 65-67—132 (-12) Rory McIlroy 67-65—132 (-12) Jim Furyk 71-64—135 (-9) Ian Poulter 69-66—135 (-9) Brian Harman 66-69—135 (-9) Abraham Ancer 69-66—135 (-9) Things to Know • Tommy Fleetwood earned his fourth 36-hole lead/co-lead with a 5-under 67 and is in search of his first PGA TOUR victory • Rory McIlroy eagled the par-5 16th and birdied the par-3 17th to card a 7-under 65 and share the 36-hole lead • Players from 11 countries have won THE PLAYERS, but none from England (Tommy Fleetwood/T1, Ian Poulter/T3) Northern Ireland (Rory McIlroy/T1) or Mexico (Abraham Ancer/T3) • Jim Furyk recorded an 8-under 64 for his lowest 18-hole score in 80 career rounds at TPC Sawgrass • Tiger Woods made a quadruple-bogey 7 at No. 17 for his highest score at that hole in 69 total rounds • Sergio Garcia extended his record consecutive cuts-made streak at THE PLAYERS to 16 Second-Round Lead Notes 13 Second-round leaders/co-leaders to win THE PLAYERS (most recent: Webb Simpson/2018) 10 Second-round leaders/co-leaders to win in 2018-19 (most recent: Keith Mitchell/The Honda Classic) Comparing the co-leaders (entering the week) Tommy Fleetwood Rory McIlroy Age 28 (Jan. -

1996 John Deere Classic
ED FLORI TOTAL 1R 2R 3R 4R MONEY 1996 268 66 68 67 67 $216,000 JOHN DEERE CLASSIC Tour veteran Ed Fiori scored his third media members who had scrambled to get the Q-Cs that morning, OAKWOOD CC, COAL VALLEY, IL PGA Tour win and his first in 14 years, Woods quadruple-bogeyed the fourth hole, then four-putted at SEPT 12-15 8 months and two days, the second longest No. 8 to fall out of contention. He rallied to finish tied for fifth. PAR: 35-35-70 stretch between wins on record. Playing in his third event as a pro, Tiger Woods took his first lead on the PGA Tour with a TOTAL PURSE: second-round 64 and led Fiori by a shot heading into Sunday’s $1,200,000 final round. In front of a crowd that included a dozen national 1996 JOHN DEERE CLASSIC RANK PLAYER TOTAL 1R 2R 3R 4R MONEY RANK PLAYER TOTAL 1R 2R 3R 4R MONEY MISSED CUT TOTAL 1R 2R MISSED CUT TOTAL 1R 2R MISSED CUT TOTAL 1R 2R 2 Andrew Magee 270 69 70 69 62 $129,600 T36 Doug Martin 278 70 72 70 66 5,652 Tommy Armour III 147 75 72 Gil Morgan 147 71 76 WD Joe Acosta, Jr. 75 75 T3 Steve Jones 271 68 68 67 68 69,600 T36 Taylor Smith 278 67 69 71 71 5,652 Shane Bertsch 143 71 72 Jim Nelford 149 70 79 WD David Peoples 80 80 T3 Chris Perry 271 68 70 67 66 69,600 T41 John Adams 279 71 69 70 69 3,798 Danny Briggs 144 68 76 Mac O’Grady 144 73 71 T5 Phil Blackmar 272 69 71 65 67 42,150 T41 Bart Bryant 279 71 69 70 69 3,798 Bill Britton 146 73 73 Carl Paulson 143 71 72 T5 Jeff Maggert 272 67 68 73 64 42,150 T41 Rex Caldwell 279 68 72 71 68 3,798 Billy Ray Brown 144 71 73 Peter Persons 144 72 72 T5 -

Notes About Participants in the 2005 Funai Classic …
2017 THE PLAYERS Championship (The 27th of 43 events in the PGA TOUR Season) Ponte Vedra Beach, Fla. May 11-14, 2017 FedExCup Points: 600 THE PLAYERS Stadium Par/Yardage: 36-36—72/7,189 Purse: $10,500,000 ($1,890,000) TPC Sawgrass First-Round Notes – Thursday, May 11, 2017 Weather: Mostly sunny with a high of 91. Wind WSW 8-16 mph. First-Round Leaderboard William McGirt 67 (-5) Mackenzie Hughes 67 (-5) J.B. Holmes 68 (-4) Alex Noren 68 (-4) Chez Reavie 68 (-4) Jon Rahm 68 (-4) William McGirt William McGirt posted the best round of the morning wave with a 5-under 67 to share the lead with first-timer Mackenzie Hughes. This marks the fifth time McGirt has held the lead or a share of the lead after 18 holes. In four prior tries, he has failed to convert the opening round lead into a victory or top-five. McGirt eagled Nos. 11 and 16, becoming the 27th player to record two eagles in one round at THE PLAYERS and the sixth to do so on the back nine. Last year, two players recorded two eagles in one round: Kevin Chappell (R3); and Louis Oosthuizen (R4). In four prior starts at TPC Sawgrass, McGirt’s only other sub-70 round was a 7-under 65 in the second round in 2016. In two previous made cuts, McGirt finished T43 both times, including his debut in 2013 and last year. This is the fifth time McGirt has held the lead or a share of the lead after 18 holes. -

January 3, 1999
January 03 1999 Official World Golf Ranking Week 1 / 1999 1997 / 1998 1999 Points Total No of Points Points Ranking Player Country Average Points Events Lost Gained 1 (1) Tiger Woods USA 12.30 566.00 46 0.00 + 0.00 2 (2) Mark O'Meara USA 10.43 532.00 51 0.00 + 0.00 3 (3) David Duval USA 9.67 532.00 55 0.00 + 0.00 4 (4) Davis Love-III USA 9.22 461.00 50 -20.00 + 0.00 5 (5) Ernie Els SAf 9.13 493.00 54 -12.00 + 0.00 6 (6) Nick Price Zim 9.04 452.00 50 -6.00 + 0.00 7 (9) Vijay Singh Fij 8.66 502.00 58 0.00 + 0.00 8 (8) Lee Westwood Eng 8.65 536.00 62 0.00 + 0.00 9 (7) Colin Montgomerie Sco 8.45 473.00 56 -35.00 + 0.00 10 (10) Phil Mickelson USA 7.65 390.00 51 -6.00 + 0.00 11 (11) Fred Couples USA 7.58 303.00 40 -3.00 + 0.00 12 (12) Jim Furyk USA 7.23 412.00 57 0.00 + 0.00 13 (13) Masashi Ozaki Jpn 6.77 318.00 47 0.00 + 0.00 14 (14) Jesper Parnevik Swe 6.60 330.00 50 0.00 + 0.00 15 (15) Justin Leonard USA 6.42 385.00 60 0.00 + 0.00 16 (16) Steve Elkington Aus 5.95 238.00 40 -9.00 + 0.00 17 (17) Darren Clarke NIr 5.67 323.00 57 -3.00 + 0.00 18 (19) Brian Watts USA 5.23 251.00 48 0.00 + 0.00 19 (21) Mark Calcavecchia USA 5.19 301.00 58 0.00 + 0.00 20 (22) Tom Lehman USA 5.12 261.00 51 -3.00 + 0.00 21= (20) Scott Hoch USA 5.00 270.00 54 -17.00 + 0.00 21= (23) Lee Janzen USA 5.00 270.00 54 -6.00 + 0.00 23 (18) Greg Norman Aus 4.91 211.00 43 -32.00 + 0.00 24 (24) Tom Watson USA 4.75 190.00 40 0.00 + 0.00 25 (25) Jose M Olazabal Spn 4.62 245.00 53 0.00 + 0.00 26 (26) Steve Stricker USA 4.60 198.00 43 0.00 + 0.00 27 (27) Payne Stewart USA 4.49 220.00 -

Andrew Coltart
Andrew Coltart Representerar Skottland (SCO) Född Status Proffs Huvudtour SGT-spelare Nej Aktuellt Ranking 2021 Andrew Coltart har inte startat säsongen. Karriären Totala prispengar 1997-2021 Andrew Coltart har följande facit så här långt i karriären: (officiella prispengar på SGT och världstourerna) Summa Största Snitt per 2 segrar på 404 tävlingar. För att vinna dessa 2 tävlingar har det krävts en snittscore om 68,38 kronor prischeck tävling slag, eller totalt -29 mot par. I snitt per vunnen tävling gick Andrew Coltart -14,50 i förhållande År Tävl mot par. Segrarna har varit värda 3 315 691 kr. 1997 30 1 795 867 239 730 59 862 Härutöver har det också blivit: 1998 28 5 710 743 1 441 000 203 955 - 5 andraplatser. - 6 tredjeplatser. 1999 28 4 058 179 835 214 144 935 - 41 övriga topp-10-placeringar 2000 28 6 631 921 1 541 592 236 854 - 35 placeringar inom 11-20 2001 28 6 297 951 1 987 462 224 927 - 163 övriga placeringar på rätt sida kvalgränsen - 1 missade kval 2002 33 4 165 192 950 013 126 218 Med 252 klarade kval på 253 starter är kvalprocenten sålunda 100. 2003 30 5 815 710 903 136 193 857 Sammantaget har Andrew Coltart en snittscore om 71,65 slag, eller totalt -56 mot par. 2004 28 883 632 180 578 31 558 2005 28 2 519 353 785 465 89 977 2006 26 2 653 318 1 048 873 102 051 2007 27 1 116 085 302 522 41 336 2008 21 780 087 229 570 37 147 2009 29 2 592 750 463 548 89 405 2010 24 1 013 077 146 117 42 212 2011 6 104 677 44 359 17 446 Totalt 46 390 489 Bästa placeringarna • Segrar (2 st) Estoril Open Greg Norman Holden International The Great -

Better '09 for State's PGA Tour Pros?
GEORGIAPGA.COM GOLFFOREGEORGIA.COM «« FEBRUARY 2009 Better ’09 for state’s PGA Tour pros? Love, Howell off to quick early starts By Mike Blum nament in ’08, as did former Georgia sixth in regular season points for the ’09 opener, placing him within range of or most of Georgia’s contingent Bulldog Ryuji Imada . FedEdCup and ninth on the final money the top 50 in the World Rankings and a on the PGA Tour, the 2008 The rest of Georgia’s PGA Tour mem - list with almost $4 million. Masters berth. season was not a particularly bers had to wait another week or two to Cink’s ‘08 season was divided into two Imada scored his first PGA Tour win in F memorable one, although there start their ’09 campaigns, with a common disparate halves; before and after his win in four seasons in Atlanta, but will not get the were some exceptions. theme the hope that this year will be a Hartford. Other than his participation on opportunity to defend his title in the Duluth’s Stewart Cink more successful one than 2008. the Ryder Cup team, Cink’s post-victory defunct AT&T Classic. Imada had a pair and Sea Island’s Davis On the surface, Cink’s ‘08 season was an highlights were non-existent. And as well of runner-up finishes among three top- Love opened the extremely successful one. He scored his as he played the first six months of the fives early in ’08 and a near win in the Fall 2009 season in the first win in five years in Hartford, the site season, he let a win get away in Tampa and Series, ending the season 13th in earnings Mercedes-Benz of his first PGA Tour victory as a rookie in did not put up much of a fight in the with over $3 million. -
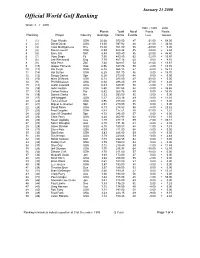
Week 03 Ranking
January 23 2000 Official World Golf Ranking Week 3 / 2000 1998 / 1999 2000 Points Total No of Points Points Ranking Player Country Average Points Events Lost Gained 1 (1) Tiger Woods USA 20.68 972.00 47 -21.00 + 54.00 2 (2) David Duval USA 13.00 597.92 46 -41.00 + 33.92 3 (3) Colin Montgomerie Sco 10.02 551.00 55 -29.00 + 0.00 4 (4) Davis Love-III USA 8.99 404.44 45 -34.00 + 2.44 5 (5) Ernie Els SAf 8.94 500.40 56 -28.00 + 44.40 6 (7) Vijay Singh Fij 7.80 483.80 62 -12.00 + 10.80 7 (6) Lee Westwood Eng 7.79 467.16 60 0.00 + 4.16 8 (8) Nick Price Zim 7.40 369.87 50 -11.00 + 13.87 9 (15) Jesper Parnevik Swe 6.96 347.76 50 -2.00 + 83.76 10 (11) Jim Furyk USA 6.42 366.18 57 -6.00 + 16.18 11 (14) Hal Sutton USA 6.28 351.70 56 0.00 + 15.70 12 (12) Sergio Garcia Spn 6.20 273.00 44 0.00 + 0.00 13 (10) Mark O'Meara USA 6.13 288.00 47 -38.00 + 0.00 14 (9) Phil Mickelson USA 6.04 296.20 49 -37.00 + 4.20 15 (13) Justin Leonard USA 6.03 349.93 58 -8.00 + 1.93 16 (16) John Huston USA 5.60 302.65 54 -8.00 + 26.65 17 (18) Carlos Franco Par 5.42 265.76 49 0.00 + 16.76 18 (19) Darren Clarke NIr 5.33 293.00 55 -3.00 + 0.00 19 (17) Jeff Maggert USA 5.17 253.16 49 -9.00 + 11.16 20 (22) Tom Lehman USA 4.96 238.00 48 -3.00 + 9.00 21 (21) Miguel A Jimenez Spn 4.91 270.00 55 0.00 + 0.00 22 (24) David Toms USA 4.73 274.52 58 -4.00 + 23.52 23 (20) Fred Couples USA 4.44 177.51 40 -31.00 + 1.51 24 (26) Jose M Olazabal Spn 4.32 246.00 57 0.00 + 0.00 25 (23) Chris Perry USA 4.24 262.93 62 -13.00 + 1.93 26 (35) Stuart Appleby Aus 4.19 247.14 59 -7.00 + 35.14 27 (25) -

2018 Rapiscan Systems Classic Presented by Coastal Mississippi Media Guide
Rapiscan Systems Classic March 19 – 25, 2018 | Fallen Oak RapiscanSystemsClassic.com QUICK FACTS Title Sponsor: Rapiscan Systems Location: Fallen Oak, 24400 Highway 15 North, Biloxi, Mississippi 39574 Purse: $1.6 million ($240,000 to winner) Field: 78 players Format: 18-hole stroke play (three rounds) Par & Yardage: Fallen Oak is par 36-36=72 and will be set up at 7,118 yards Previous Winners: 2017 Champion - Miguel Angel Jimenez (203, -13) 2016 Champion - Miguel Angel Jimenez (202, -14) 2015 Champion - David Frost (206, -10) 2014 Champion - Jeff Maggert (205, -11) 2013 Champion - Michael Allen (205, -11) 2012 Champion - Fred Couples (202, -14) 2011 Champion - Tom Lehman (200, -16) 2010 Champion - David Eger (205, -11) Officials Pro-Ams: Wednesday Pro-Am., Mar. 21 at 7:00 am (Split Tee Times) Thursday Pro-Am., Mar. 22 at 7:00 am (Split Tee Times) Tournament Play: Fri., Mar. 23 at approximately 10:00 am (Split Tee Times) Sat., Mar. 24 at approximately 11:00 am (Split Tee Times) Sun., Mar. 25 at approximately 11:00 am (Split Tee Times) Television Coverage: Fri., Mar. 23, 9:30 - 11:30 pm (The Golf Channel, Tape Delayed) Sat., Mar. 24, 4:00 - 6:00 pm (The Golf Channel, Live) Sun., Mar. 25, 4:00 - 6:00 pm (The Golf Channel, Live) Tickets: General admission is free compliments of Rapiscan Systems and Coca-Cola Economic Impact: Over $100 million since 2010 Benefitting Charity: Local charities throughout region - Birdies for Charity program Event Management: Bruno Event Team – www.brunoeventteam.com *- All times are Central, approximate and subject -

2000-2009 Section History.Pub
A Chronicle of the Philadelphia Section PGA and its Members by Peter C. Trenham 2000 to 2009 2000 Jack Connelly was elected president of the PGA of America and John DiMarco won the New Jersey Open 2001 Terry Hatch won the stroke play and the match play tournaments at the PGA winter activities in Port St. Lucie 2002 The Section hosted the PGA of America national meeting at the Wyndham Franklin Plaza Hotel in Philadelphia 2003 Jim Furyk won the U.S. Open, Greg Farrow won the N.J. Open, Tom Carter won 3 times on the Nationwide Tour 2004 Pete Oakley won the Senior British Open 2005 Will Reilly was the PGA of America’s “ Junior Golf Leader” and Rich Steinmetz was on the PGA Cup Team 2006 Jim Furyk played on his fifth straight Ryder Cup Team, won the Vardon Trophy and two PGA Tour events 2007 In October the Philadelphia PGA and the Variety Club broke ground on the Variety Club’s 3-hole golf course 2008 Tom Carpus won the PGA of America’s Horton Smith Award and Hugh Reilly received the President Plaque 2009 Mark Sheftic finished second in the PGA Professional National Championship and played on the PGA Cup Team 2000 Jim Furyk won the Doral Open on the Doral Golf Resort’s Blue Course in the first week of March. The course nicknamed the “ Blue Monster” had been toughened in 1996 by adding 27 bunkers, which most of the play- ers didn’t care for. In 1999 the course had been reworked to its original Dick Wilson design, but now most of the players thought the course was too easy. -
Thursday MPCC Shore 1St Tee 8:00 Whee Kim and Louis Welch (12) Tom Gillis and Alan Hoops (13) 8:11 Blake Adams and Michael J
Thursday MPCC Shore 1st Tee 8:00 Whee Kim and Louis Welch (12) Tom Gillis and Alan Hoops (13) 8:11 Blake Adams and Michael J. Fitzpatrick (5) Greg Chalmers and Jeffrey Henley (11) 8:22 Tyrone Van Aswegen and George Davis (4) Andrew Loupe and Murray Demo (5) 8:33 Lucas Lee and Patrick Hamill (10) Abraham Ancer and Wes Heyward (17) 8:44 Andres Romero and Sean Kell (11) Robert Garrigus and Hank Plain (9) 8:55 Troy Merritt and Michael McCallister (7) Vijay Singh and Shantanu Narayen (9) 9:06 Chez Reavie and Brian Swette (9) Bryce Molder and Harry You (15) 9:17 Brian Stuard and Tom Dreesen (9) Luke Guthrie and Willy Strothotte (13) 9:28 Tom Hoge and Royal Cole (7) Henrik Norlander and Donald Boeding (12) 9:39 Scott Langley and Tom Nelson (8) Cameron Smith and Jim Davis (3) 9:50 John Rollins and Dan Rose (10) Russell Henley and Rob Light (11) 10:01 Jonas Blixt and Jamie Williamson (9) Dicky Pride and John Stafford III (8) 10:12 Martin Piller and Joe O'Neil (18) Andrew Landry and Greg Buonocore (18) 10th Tee 8:00 Ricky Barnes and Jerry Tarde (9) Jim Herman and Jim Tullis (9) 8:11 Jason Dufner and Josh Donaldson (3) Pat Perez and Michael Lund (5) 8:22 Sean O'Hair and Greg Johnson (9) Chesson Hadley and Joe Lacob (10) 8:33 Bronson Burgoon and Carl Lindner III (16) Miguel Angel Carballo and Brian Ferris (1) 8:44 Nicholas Thompson and Andy Garcia (8) David Hearn and David Dube (10) 8:55 Brendon Todd and Pat Battle (3) David Lingmerth and Stuart Francis (3) 9:06 Jason Kokrak and Ed Vaughan (10) Kevin Na and Kenny G (3) 9:17 Jason Bohn and Condoleezza Rice (15) Jonathan Byrd and David Seaton (10) 9:28 Wes Roach and Annesley MacFarlane (8) Billy Hurley III and Julie Frist (8) 9:39 David Duval and T. -

2015 Puerto Rico Open (The 17Th of 43 Events in the PGA TOUR Season)
2015 Puerto Rico Open (The 17th of 43 events in the PGA TOUR Season) Rio Grande, Puerto Rico March 2-8, 2015 Purse: $3,000,000 (winner: $540,000) Trump International Golf Club Par/Yards: 72/7,506 First-Round Notes – Thursday, March 5, 2015 Weather: Mostly sunny with temperatures in the mid 80s. Winds ENE 15-25 mph. First-Round Leaderboard Mark Hubbard 68 (-4) Chris Smith 69 (-3) Emilliano Grillo 69 (-3) Billy Mayfair 69 (-3) Mark Hubbard PGA TOUR rookie Mark Hubbard is making his 11th start of the 2014-15 PGA TOUR Season and the 13th start of his career. He has made seven of nine cuts with a best finish of T20 at the Humana Challenge. Hubbard had an eventful February after proposing to his girlfriend at No. 18 at Pebble Beach after round one of the AT&T Pebble Beach National Pro-Am. Two weeks later he was DQ’d from The Honda Classic for failing to register. Hubbard’s previous best position after 18 holes on TOUR was T14 at the 2014 Sanderson Farms Championship. The Puerto Rico Open has historically been a stop for future Rookies of the Year. In 2014, Chesson Hadley won en route to being named the 2014 PGA TOUR Rookie of the Year. In 2013, Jordan Spieth recorded a T2 finish, one of nine top-10s that would lead to PGA TOUR Rookie of the Year. Chris Smith Smith is looking for his first top 10 on the PGA TOUR since the 2005 U.S. Bank Championship in Milwaukee (T5).