The Most Significant Mathematician of All Time, Leonhard Euler Was Born in Basel in 1707
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -
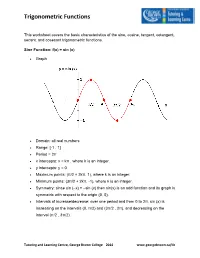
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

A MATHEMATICIAN's SURVIVAL GUIDE 1. an Algebra Teacher I
A MATHEMATICIAN’S SURVIVAL GUIDE PETER G. CASAZZA 1. An Algebra Teacher I could Understand Emmy award-winning journalist and bestselling author Cokie Roberts once said: As long as algebra is taught in school, there will be prayer in school. 1.1. An Object of Pride. Mathematician’s relationship with the general public most closely resembles “bipolar” disorder - at the same time they admire us and hate us. Almost everyone has had at least one bad experience with mathematics during some part of their education. Get into any taxi and tell the driver you are a mathematician and the response is predictable. First, there is silence while the driver relives his greatest nightmare - taking algebra. Next, you will hear the immortal words: “I was never any good at mathematics.” My response is: “I was never any good at being a taxi driver so I went into mathematics.” You can learn a lot from taxi drivers if you just don’t tell them you are a mathematician. Why get started on the wrong foot? The mathematician David Mumford put it: “I am accustomed, as a professional mathematician, to living in a sort of vacuum, surrounded by people who declare with an odd sort of pride that they are mathematically illiterate.” 1.2. A Balancing Act. The other most common response we get from the public is: “I can’t even balance my checkbook.” This reflects the fact that the public thinks that mathematics is basically just adding numbers. They have no idea what we really do. Because of the textbooks they studied, they think that all needed mathematics has already been discovered. -

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

The "Greatest European Mathematician of the Middle Ages"
Who was Fibonacci? The "greatest European mathematician of the middle ages", his full name was Leonardo of Pisa, or Leonardo Pisano in Italian since he was born in Pisa (Italy), the city with the famous Leaning Tower, about 1175 AD. Pisa was an important commercial town in its day and had links with many Mediterranean ports. Leonardo's father, Guglielmo Bonacci, was a kind of customs officer in the North African town of Bugia now called Bougie where wax candles were exported to France. They are still called "bougies" in French, but the town is a ruin today says D E Smith (see below). So Leonardo grew up with a North African education under the Moors and later travelled extensively around the Mediterranean coast. He would have met with many merchants and learned of their systems of doing arithmetic. He soon realised the many advantages of the "Hindu-Arabic" system over all the others. D E Smith points out that another famous Italian - St Francis of Assisi (a nearby Italian town) - was also alive at the same time as Fibonacci: St Francis was born about 1182 (after Fibonacci's around 1175) and died in 1226 (before Fibonacci's death commonly assumed to be around 1250). By the way, don't confuse Leonardo of Pisa with Leonardo da Vinci! Vinci was just a few miles from Pisa on the way to Florence, but Leonardo da Vinci was born in Vinci in 1452, about 200 years after the death of Leonardo of Pisa (Fibonacci). His names Fibonacci Leonardo of Pisa is now known as Fibonacci [pronounced fib-on-arch-ee] short for filius Bonacci. -

Brief History of the Early Development of Theoretical and Experimental Fluid Dynamics
Brief History of the Early Development of Theoretical and Experimental Fluid Dynamics John D. Anderson Jr. Aeronautics Division, National Air and Space Museum, Smithsonian Institution, Washington, DC, USA 1 INTRODUCTION 1 Introduction 1 2 Early Greek Science: Aristotle and Archimedes 2 As you read these words, there are millions of modern engi- neering devices in operation that depend in part, or in total, 3 DA Vinci’s Fluid Dynamics 2 on the understanding of fluid dynamics – airplanes in flight, 4 The Velocity-Squared Law 3 ships at sea, automobiles on the road, mechanical biomedi- 5 Newton and the Sine-Squared Law 5 cal devices, and so on. In the modern world, we sometimes take these devices for granted. However, it is important to 6 Daniel Bernoulli and the Pressure-Velocity pause for a moment and realize that each of these machines Concept 7 is a miracle in modern engineering fluid dynamics wherein 7 Henri Pitot and the Invention of the Pitot Tube 9 many diverse fundamental laws of nature are harnessed and 8 The High Noon of Eighteenth Century Fluid combined in a useful fashion so as to produce a safe, efficient, Dynamics – Leonhard Euler and the Governing and effective machine. Indeed, the sight of an airplane flying Equations of Inviscid Fluid Motion 10 overhead typifies the laws of aerodynamics in action, and it 9 Inclusion of Friction in Theoretical Fluid is easy to forget that just two centuries ago, these laws were Dynamics: the Works of Navier and Stokes 11 so mysterious, unknown or misunderstood as to preclude a flying machine from even lifting off the ground; let alone 10 Osborne Reynolds: Understanding Turbulent successfully flying through the air. -

The Astronomers Tycho Brahe and Johannes Kepler
Ice Core Records – From Volcanoes to Supernovas The Astronomers Tycho Brahe and Johannes Kepler Tycho Brahe (1546-1601, shown at left) was a nobleman from Denmark who made astronomy his life's work because he was so impressed when, as a boy, he saw an eclipse of the Sun take place at exactly the time it was predicted. Tycho's life's work in astronomy consisted of measuring the positions of the stars, planets, Moon, and Sun, every night and day possible, and carefully recording these measurements, year after year. Johannes Kepler (1571-1630, below right) came from a poor German family. He did not have it easy growing Tycho Brahe up. His father was a soldier, who was killed in a war, and his mother (who was once accused of witchcraft) did not treat him well. Kepler was taken out of school when he was a boy so that he could make money for the family by working as a waiter in an inn. As a young man Kepler studied theology and science, and discovered that he liked science better. He became an accomplished mathematician and a persistent and determined calculator. He was driven to find an explanation for order in the universe. He was convinced that the order of the planets and their movement through the sky could be explained through mathematical calculation and careful thinking. Johannes Kepler Tycho wanted to study science so that he could learn how to predict eclipses. He studied mathematics and astronomy in Germany. Then, in 1571, when he was 25, Tycho built his own observatory on an island (the King of Denmark gave him the island and some additional money just for that purpose). -

The Bernoulli Edition the Collected Scientific Papers of the Mathematicians and Physicists of the Bernoulli Family
Bernoulli2005.qxd 24.01.2006 16:34 Seite 1 The Bernoulli Edition The Collected Scientific Papers of the Mathematicians and Physicists of the Bernoulli Family Edited on behalf of the Naturforschende Gesellschaft in Basel and the Otto Spiess-Stiftung, with support of the Schweizerischer Nationalfonds and the Verein zur Förderung der Bernoulli-Edition Bernoulli2005.qxd 24.01.2006 16:34 Seite 2 The Scientific Legacy Èthe Bernoullis' contributions to the theory of oscillations, especially Daniel's discovery of of the Bernoullis the main theorems on stationary modes. Johann II considered, but rejected, a theory of Modern science is predominantly based on the transversal wave optics; Jacob II came discoveries in the fields of mathematics and the tantalizingly close to formulating the natural sciences in the 17th and 18th centuries. equations for the vibrating plate – an Eight members of the Bernoulli family as well as important topic of the time the Bernoulli disciple Jacob Hermann made Èthe important steps Daniel Bernoulli took significant contributions to this development in toward a theory of errors. His efforts to the areas of mathematics, physics, engineering improve the apparatus for measuring the and medicine. Some of their most influential inclination of the Earth's magnetic field led achievements may be listed as follows: him to the first systematic evaluation of ÈJacob Bernoulli's pioneering work in proba- experimental errors bility theory, which included the discovery of ÈDaniel's achievements in medicine, including the Law of Large Numbers, the basic theorem the first computation of the work done by the underlying all statistical analysis human heart. -

Newton.Indd | Sander Pinkse Boekproductie | 16-11-12 / 14:45 | Pag
omslag Newton.indd | Sander Pinkse Boekproductie | 16-11-12 / 14:45 | Pag. 1 e Dutch Republic proved ‘A new light on several to be extremely receptive to major gures involved in the groundbreaking ideas of Newton Isaac Newton (–). the reception of Newton’s Dutch scholars such as Willem work.’ and the Netherlands Jacob ’s Gravesande and Petrus Prof. Bert Theunissen, Newton the Netherlands and van Musschenbroek played a Utrecht University crucial role in the adaption and How Isaac Newton was Fashioned dissemination of Newton’s work, ‘is book provides an in the Dutch Republic not only in the Netherlands important contribution to but also in the rest of Europe. EDITED BY ERIC JORINK In the course of the eighteenth the study of the European AND AD MAAS century, Newton’s ideas (in Enlightenment with new dierent guises and interpre- insights in the circulation tations) became a veritable hype in Dutch society. In Newton of knowledge.’ and the Netherlands Newton’s Prof. Frans van Lunteren, sudden success is analyzed in Leiden University great depth and put into a new perspective. Ad Maas is curator at the Museum Boerhaave, Leiden, the Netherlands. Eric Jorink is researcher at the Huygens Institute for Netherlands History (Royal Dutch Academy of Arts and Sciences). / www.lup.nl LUP Newton and the Netherlands.indd | Sander Pinkse Boekproductie | 16-11-12 / 16:47 | Pag. 1 Newton and the Netherlands Newton and the Netherlands.indd | Sander Pinkse Boekproductie | 16-11-12 / 16:47 | Pag. 2 Newton and the Netherlands.indd | Sander Pinkse Boekproductie | 16-11-12 / 16:47 | Pag. -

Famous Mathematicians Key
Infinite Secrets AIRING SEPTEMBER 30, 2003 Learning More Dzielska, Maria. Famous Mathematicians Hypatia of Alexandria. Cambridge, MA: Harvard University The history of mathematics spans thousands of years and touches all parts of the Press, 1996. world. Likewise, the notable mathematicians of the past and present are equally Provides a biography of Hypatia based diverse.The following are brief biographies of three mathematicians who stand out on several sources,including the letters for their contributions to the fields of geometry and calculus. of Hypatia’s student Synesius. Hypatia of Alexandria Bhaskara wrote numerous papers and Biographies of Women Mathematicians books on such topics as plane and spherical (c. A.D. 370–415 ) www.agnesscott.edu/lriddle/women/ Born in Alexandria, trigonometry, algebra, and the mathematics women.htm of planetary motion. His most famous work, Contains biographical essays and Egypt, around A.D. 370, Siddhanta Siromani, was written in A.D. comments on woman mathematicians, Hypatia was the first 1150. It is divided into four parts: “Lilavati” including Hypatia. Also includes documented female (arithmetic), “Bijaganita” (algebra), resources for further study. mathematician. She was ✷ ✷ ✷ the daughter of Theon, “Goladhyaya” (celestial globe), and a mathematician who “Grahaganita” (mathematics of the planets). Patwardhan, K. S., S. A. Naimpally, taught at the school at the Alexandrine Like Archimedes, Bhaskara discovered and S. L. Singh. Library. She studied astronomy, astrology, several principles of what is now calculus Lilavati of Bhaskaracharya. centuries before it was invented. Also like Delhi, India:Motilal Banarsidass, 2001. and mathematics under the guidance of her Archimedes, Bhaskara was fascinated by the Explains the definitions, formulae, father.She became head of the Platonist concepts of infinity and square roots. -

Leonhard Euler: His Life, the Man, and His Works∗
SIAM REVIEW c 2008 Walter Gautschi Vol. 50, No. 1, pp. 3–33 Leonhard Euler: His Life, the Man, and His Works∗ Walter Gautschi† Abstract. On the occasion of the 300th anniversary (on April 15, 2007) of Euler’s birth, an attempt is made to bring Euler’s genius to the attention of a broad segment of the educated public. The three stations of his life—Basel, St. Petersburg, andBerlin—are sketchedandthe principal works identified in more or less chronological order. To convey a flavor of his work andits impact on modernscience, a few of Euler’s memorable contributions are selected anddiscussedinmore detail. Remarks on Euler’s personality, intellect, andcraftsmanship roundout the presentation. Key words. LeonhardEuler, sketch of Euler’s life, works, andpersonality AMS subject classification. 01A50 DOI. 10.1137/070702710 Seh ich die Werke der Meister an, So sehe ich, was sie getan; Betracht ich meine Siebensachen, Seh ich, was ich h¨att sollen machen. –Goethe, Weimar 1814/1815 1. Introduction. It is a virtually impossible task to do justice, in a short span of time and space, to the great genius of Leonhard Euler. All we can do, in this lecture, is to bring across some glimpses of Euler’s incredibly voluminous and diverse work, which today fills 74 massive volumes of the Opera omnia (with two more to come). Nine additional volumes of correspondence are planned and have already appeared in part, and about seven volumes of notebooks and diaries still await editing! We begin in section 2 with a brief outline of Euler’s life, going through the three stations of his life: Basel, St.