DOCSLIB.ORG

Cit 907 Course Title: Advanced Operations Research (3 Units)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cit 907 Course Title: Advanced Operations Research (3 Units) NATIONAL OPEN UNIVERSITY OF NIGERIA FACULTY OF SCIENCES COURSE CODE: CIT 907 COURSE TITLE: ADVANCED OPERATIONS RESEARCH (3 UNITS) 1 COURSE GUIDE CIT 907: ADVANCED OPERATIONS RESEARCH UNITS: 3 Course Team Course Developer/Writer Dr. Ogonnaya Michael Romanus African University of Science and Technology, Abuja Dr. Gregory Onwodi – NOUN Dr. Maduabuchi Ejike Okpala – Baze University, Abuja. Content Editor Prof. Benjamin Aribisala. LASU Course Material Coordination Dr. Vivian Nwaocha, Dr. Greg Onwodi & Dr. Francis B.Osang Department of Computer Science National Open University of Nigeria NATIONAL OPEN UNIVERSITY OF NIGERIA Headquarters Plot 91, Cadastral Zone, Nnamdi Azikiwe Expressway, Jabi – Abuja, Nigeria Lagos Office 14/16 Ahmadu Bello Way Victoria Island Lagos e-mail: [email protected] URL: www.nou.edu.ng Published by National Open University of Nigeria Printed 2020 ISBN: All Rights Reserved 2 Contents COURSE GUIDE ................................................................................................................. 2 INTRODUCTION ................................................................................................................ 4 THE COURSE ..................................................................................................................... 4 COURSE AIMS AND OBJECTIVES ........................................................................................ 4 WORKING THROUGH THIS COURSE ................................................................................... 5 COURSE MATERIALS ......................................................................................................... 5 STUDY UNITS .................................................................................................................... 5 TEXTBOOKS/REFERENCES ................................................................................................. 6 ASSESSMENT .................................................................................................................... 6 SELF-ASSESSMENT EXERCISES ........................................................................................... 6 END OF COURSE EXAMINATION ........................................................................................ 6 SUMMARY ....................................................................................................................... 7 MODULE 1 : LINEAR PROGRAMMING IN OPERATION RESEARCH .................................... 8 UNIT 1 CONCEPTS OF OPERATIONS RESEARCH ................................................................. 8 UNIT 2 MODELLING IN OPERATIONS RESEARCH .............................................................. 17 UNIT 3 LINEAR PROGRAMMING (1) ................................................................................. 23 UNIT 4 LINEAR PROGRAMMING (2) ................................................................................. 45 UNIT 5 LINEAR PROGRAMMING (3) ................................................................................. 73 MODULE 2: OPERATION RESEARCH TECHNIQUES ............................................................ 82 UNIT 1 CONCEPT OF INTEGER PROGRAMMING ............................................................ 82 UNIT 2 THE CONCEPT OF DYNAMIC PROGRAMMING ...................................................... 90 UNIT 3 CONCEPT OF GOAL PROGRAMMING ................................................................... 95 UNIT 4 TRANSPORTATION MODEL ................................................................................ 106 UNIT 5 ASSIGNMENT MODEL ......................................................................................... 135 MODULE 3: OPERATION RESEARCH MODELLING ........................................................... 147 UNIT 1 INVENTORY MODEL............................................................................................ 147 UNIT 2 NETWORK ANALYSIS .......................................................................................... 166 UNIT 3 THE PROBLEMS IN SEQUENCING ........................................................................ 190 UNIT 4 WAITING LINE IN QUEUING THEORY ................................................................. 209 UNIT 5 REPLACEMENT THEORY ..................................................................................... 242 MODULE 4: ADVANCES IN OPERATION RESEARCH......................................................... 253 UNIT 1 THEORY OF GAMES OR COMPETITIVE STRATEGIES ............................................ 253 UNIT 2 SOLVING GAMES ................................................................................................ 259 3 INTRODUCTION You should have become familiar with the Basic Operations Research concepts introduced to you in your undergraduate course. It is the objective of this course to build upon the previous lessons learnt, and formally introduce to you the more advanced concepts with the view to reinforcing your understanding and placing you in a pivotal position to intellectually understand developmental work and research in the rapidly advancing field of operations research. THE COURSE CIT 907: Advanced Operations Research consists of 17 units distributed across three modules as follows: Module 1 is composed of 5 units Module 2 is composed of 5 units Module 3 is composed of 5 units Module 4 is composed of 2 units Module 1 guides you into the realm of operations research by explaining the different approaches to operations research problem solving. It also introduces you into the concepts of operations research which is the primary concern of unit 1. Unit 2 treats modeling, while unit 3, 4 and 5 take you through progressively, through advanced levels of linear programming. In Module 2, units 1, 2 and 3 treat integer programming, dynamic programming and goal programming respectively, while unit 4 revisits transportation model which you certainly must have encountered. This module concludes with the assignment model and discusses amongst others, the two methods of enumeration and reduced matrix which are very crucial in solving assignment problems. Furthermore, Module 3 exposes you to inventory, network analysis, sequencing, line waiting and replacement. In Module 4, unit 1 introduces the basis of game theory as well as its important principles. While in unit 2 several methods of solving games were elaborately discussed with numerous examples. COURSE AIMS AND OBJECTIVES The aim of CIT 907 is to further intimate you with operations research, acquaint you with the mathematical calculations and the practical approximation of the idealized theorems which allows you establish their practicable applications and indispensability in the real world. You should also bear in mind the practical limitations of the concepts idealized in the real world. You are required to conscientiously and diligently work through this course and upon completion of this course, you should be able to: understand the meaning of operations research highlight the historical development of operations research describe the scientific nature of operations research identify the importance and uses of operations research with respect to the various topics to be treated in the study state the limitations of operations research state the meaning of model in operations research describe the various types of model describe how to construct a model 4 list some standard operations research model state the usefulness of linear programming in operations research state the properties of a linear programming model identify some areas of application of linear programming formulate a linear programming model state the usual assumptions of a linear programming model solve a two-variable linear programming model graphically prepare LPD for use of simplex explain the use of simplex list the steps involved in using a simplex method prepare a simplex table and understand its various components demonstrate the use of simplex method for solving an LLP solve LPP using maximization problem describe optimal – dual concept describe dual formulation procedure interpret dual programming model explain the concept of game theory understand a good number of solution methods for games. WORKING THROUGH THIS COURSE This course requires you to spend quality time to read. Whereas the content of this course is quite comprehensive, it is presented in clear language with lots of illustrations that you can easily relate to. The presentation style is qualitative and descriptive. This is deliberate and it is to ensure that your attention in the course content is sustained. You should take full advantage of the tutorial sessions because this is a veritable forum for you to “rub minds” with your peers, which provides you with valuable feedback as you have the opportunity of comparing knowledge with your course mates. COURSE MATERIALS You will be provided with course materials prior to commencement of this course. The course materials will comprise your course guide as well as your study units. You will also receive a list of recommended textbooks. These textbooks are however not compulsory. STUDY UNITS You will find listed below the study units which are contained in this course and you will observe that there are three modules. Each module comprises five units each. Module 1 Linear Programming in Operation Research Unit 1 Concepts of Operations Research Unit 2 Modeling Unit 3 Linear Programming (1) Unit 4 Linear Programming (2 Unit 5 Linear Programming (3) Module
Load more

Recommended publications
  • Traveling Salesman Problem
    TRAVELING SALESMAN PROBLEM, THEORY AND APPLICATIONS Edited by Donald Davendra Traveling Salesman Problem, Theory and Applications Edited by Donald Davendra Published by InTech Janeza Trdine 9, 51000 Rijeka, Croatia Copyright © 2010 InTech All chapters are Open Access articles distributed under the Creative Commons Non Commercial Share Alike Attribution 3.0 license, which permits to copy, distribute, transmit, and adapt the work in any medium, so long as the original work is properly cited. After this work has been published by InTech, authors have the right to republish it, in whole or part, in any publication of which they are the author, and to make other personal use of the work. Any republication, referencing or personal use of the work must explicitly identify the original source. Statements and opinions expressed in the chapters are these of the individual contributors and not necessarily those of the editors or publisher. No responsibility is accepted for the accuracy of information contained in the published articles. The publisher assumes no responsibility for any damage or injury to persons or property arising out of the use of any materials, instructions, methods or ideas contained in the book. Publishing Process Manager Ana Nikolic Technical Editor Teodora Smiljanic Cover Designer Martina Sirotic Image Copyright Alex Staroseltsev, 2010. Used under license from Shutterstock.com First published December, 2010 Printed in India A free online edition of this book is available at www.intechopen.com Additional hard copies can be obtained
    [Show full text]
  • Examensarbete Computation of Mileage Limits for Traveling
    Examensarbete Computation of Mileage Limits for Traveling Salesmen by Means of Optimization Techniques Johan Torstensson LiTH - MAT - EX - - 2008 / 08 - - SE Computation of Mileage Limits for Traveling Salesmen by Means of Optimization Techniques Division of Optimization, Department of Mathematics Linköpings Universitet Johan Torstensson LiTH - MAT - EX - - 2008 / 08 - - SE Examensarbete: 30 hp Level: D Examiner: Kaj Holmberg, Division of Optimization, Department of Mathematics Linköpings Universitet Supervisor: Kaj Holmberg, Professor, Linköpings Universitet Co-supervisor: Maria Mehlin, Scantech Sverige Linköping: June 2008 Abstract Many companies have traveling salesmen that market and sell their products. This results in much traveling by car due to the daily customer visits. This causes costs for the company, in form of travel expenses compensation, and en- vironmental effects, in form of carbon dioxide pollution. As many companies are certified according to environmental management systems, such as ISO 14001, the environmental work becomes more and more important as the environmen- tal consciousness increases every day for companies, authorities and public. The main task of this thesis is to compute reasonable limits on the mileage of the salesmen; these limits are based on specific conditions for each salesman’s district. The objective is to implement a heuristic algorithm that optimizes the customer tours for an arbitrary chosen month, which will represent a “standard” month. The output of the algorithm, the computed distances, will constitute a mileage limit for the salesman. The algorithm consists of a constructive heuristic that builds an initial solution, which is modified if infeasible. This solution is then improved by a local search algorithm preceding a genetic algorithm, which task is to improve the tours separately.
    [Show full text]
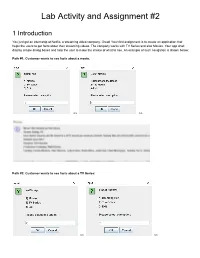
  • Lab Activity and Assignment #2
    Lab Activity and Assignment #2 1 Introduction You just got an internship at Netfliz, a streaming video company. Great! Your first assignment is to create an application that helps the users to get facts about their streaming videos. The company works with TV Series and also Movies. Your app shall display simple dialog boxes and help the user to make the choice of what to see. An example of such navigation is shown below: Path #1: Customer wants to see facts about a movie: >> >> Path #2: Customer wants to see facts about a TV Series: >> >> >> >> Your app shall read the facts about a Movie or a TV Show from text files (in some other course you will learn how to retrieve this information from a database). They are provided at the end of this document. As part of your lab, you should be creating all the classes up to Section 3 (inclusive). As part of your lab you should be creating the main Netfliz App and making sure that your code does as shown in the figures above. The Assignment is due on March 8th. By doing this activity, you should be practicing the concept and application of the following Java OOP concepts Class Fields Class Methods Getter methods Setter methods encapsulation Lists String class Split methods Reading text Files Scanner class toString method Override superclass methods Scanner Class JOptionPane Super-class sub-class Inheritance polymorphism Class Object Class Private methods Public methods FOR loops WHILE Loops Aggregation Constructors Extending Super StringBuilder Variables IF statements User Input And much more..
    [Show full text]
  • 55 “Selling US Grant's Memoirs: the Art of the Canvasser”
    “Selling U. S. Grant’s Memoirs: The Art of the Canvasser” [Note: The following paper formed the basis for chapter 2 in Walter A. Friedman, Birth of a Salesman: The Transformation of Selling in America (Harvard, 2004). ] The years after the Civil War saw an increase in the number of specialized canvassers traveling through the landscape, visiting farmers or working out of stores. There were 53,500 hucksters and peddlers in 1880 according to the census: of these, 51,000 were male and 2,500, female (and many of these women were book agents).1 Salesmen of petty goods—small, inexpensive, and easily manufactured items, like books, atlases, and lightning rods—began to perfect their techniques. Traveling from farmhouse to farmhouse, they gained notoriety, especially in agricultural newspapers, for their aggressive sales pitches. “Atlas men work upon the vanity of the public; book men hold up the attractive bait of pictorial contents, and set forth the fact that the world is simply crazy over the particular work they may be selling . ,” complained a contemporary critic. “Then there are the lightning-rod agents. People are often frightened into signing blind contracts full of hidden catches, which these agents present to them for their wares.”2 Itinerant salesmen from other industries joined these petty-goods sellers on the road. Manufacturers of more expensive machinery, such as weighing scales, sewing machines, and harvesting equipment, had begun to deploy canvassers by the mid- nineteenth century. These products were complicated to make and to operate, and they 55 required explanation and service. The early sales strategies of these machinery manufacturers influenced methods of selling in large companies throughout the twentieth century.3 But petty-goods manufacturers deserve attention, for they were particularly rigorous in working out intricate sales strategies, designed to push farmers, or more often farmers’ wives, to make a one-time purchase—or “transactional” sales, as they are known.
    [Show full text]
  • In Pursuit of the Traveling Salesman
    1: Challenges It grew out of the trio’s efforts to find solutions for a classic mathematical problem—the “Traveling Salesman” problem—which has long defied solution by man, or by the fastest computers he uses. —IBM Press Release, 1964.1 n advertising campaign by Procter & Gamble caused a stir among A applied mathematicians in the spring of 1962. The campaign featured a contest with a $10,000 prize. Enough to purchase a house at the time. From the official rules: Imagine that Toody and Muldoon want to drive around the country and visit each of the 33 locations represented by dots on the contest map, and that in doing so, they want to travel the shortest possible route. You should plan a route for them from location to location which will result in the shortest total mileage from Chicago, Illinois back to Chicago, Illinois. Police officers Toody and Muldoon navigated Car 54 in a popular American television series. Their 33-city task is an instance of the traveling salesman problem,orTSP for short. In its general form, we are given a collection of cities and the distance to travel between each pair of them. The problem is to find the shortest route to visit each city and to return to the starting point. Is the general problem easy, hard, or impossible? The short answer is that no one really knows. This is both the mystery and attraction of this famous challenge in computational mathematics. And much more than a struggling salesman is at stake. The TSP is the focal point of a larger debate on the nature of complexity and possible limits to human knowledge.
    [Show full text]
  • Suchard and the Emergence of Traveling Salesmen in Switzerland, 1860–1920
    Zurich Open Repository and Archive University of Zurich Main Library Strickhofstrasse 39 CH-8057 Zurich www.zora.uzh.ch Year: 2008 Suchard and the emergence of traveling salesmen in Switzerland, 1860–1920 Rossfeld, Roman Abstract: Based on theoretical findings of the new institutional economics, this examination of the history of the Swiss chocolate company Suchard (founded in 1826) and the Verband Reisender Kaufleute der Schweiz (Association of Swiss Commercial Travelers) describes the economic significance, social image, and everyday life of traveling salesmen between 1860 and 1920. By 1900, commercial travelers formed a critical link between the enterprise and the market, helping to drive the vertical integration of production and distribution. They enjoyed high standing within the company, and many were promoted to executive levels. Traveling salesmen were largely responsible for procuring information and expanding product sales in an era that preceded specialized market research and the domination of advertising companies. DOI: https://doi.org/10.1017/S0007680500063182 Posted at the Zurich Open Repository and Archive, University of Zurich ZORA URL: https://doi.org/10.5167/uzh-9251 Journal Article Published Version Originally published at: Rossfeld, Roman (2008). Suchard and the emergence of traveling salesmen in Switzerland, 1860–1920. Business History Review, 82(4):735-759. DOI: https://doi.org/10.1017/S0007680500063182 Roman Rossfeld Suchard and the Emergence of Traveling Salesmen in Switzerland, 1860-1920 Based on theoretical findings of the new institutional econom- ics, this examination of the history of the Swiss chocolate company Suchard (founded in 1826) and the Verband Rei- sender Kaufleute der Schweiz (Association of Swiss Commer- cial Travelers) describes the economic significance, social im- age, and everyday life of traveling salesmen between i860 and 1920.
    [Show full text]
  • Home Is Where the Work Is Women, Direct Sales, and Technologies of Gender by Tiffany Lamoreaux
    Home is Where the Work is Women, Direct Sales, and Technologies of Gender by Tiffany Lamoreaux A Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Approved April 2013 by the Graduate Supervisory Committee: Ann Hibner Koblitz, Chair Mary Fonow Karen Leong ARIZONA STATE UNIVERSITY May 2013 ABSTRACT This dissertation examines how direct selling organizations compel women to believe that direct selling is, among other things, centered on the needs of women. Drawing upon feminist interdisciplinary methodologies, this dissertation brings together qualitative, archival, and ethnographic materials to analyze direct selling through a technologies of gender framework. I argue that multi-level marketing direct selling companies (like Avon, Tupperware, Mary Kay, etc.) are able to turn belief into profits because they strategically tap into gender ideologies. I show that discursive technologies of gender coalesce with race and class discourses and are put to work by direct selling companies to construct a specific type of direct seller. This dissertation attempts to unpack the complex technologies of gender that direct selling women engage with while constructing their identities as workers and women. I argue that the companies in this study deliberately tap into women's anxieties and desires to blend their perceived gender roles with their need for income. I find that direct selling companies are exceptional at branding their businesses as uniquely suited for women and that this branding hinges upon the construction of a direct sales imaginary. I argue that the direct sales imaginary taps into powerful discourses of race, class, and gender to market the American dream to women who are seeking out a space that is empowering and inclusive.
    [Show full text]
  • Suchard and the Emergence of Traveling Salesmen in Switzerland, 1860-1920
    Roman Rossfeld Suchard and the Emergence of Traveling Salesmen in Switzerland, 1860-1920 Based on theoretical findings of the new institutional econom- ics, this examination of the history of the Swiss chocolate company Suchard (founded in 1826) and the Verband Rei- sender Kaufleute der Schweiz (Association of Swiss Commer- cial Travelers) describes the economic significance, social im- age, and everyday life of traveling salesmen between i860 and 1920. By 1900, commercial travelers formed a critical link be- tween the enterprise and the market, helping to drive the ver- tical integration of production and distribution. They enjoyed high standing within the company, and many were promoted to executive levels. Traveling salesmen were largely respon- sible for procuring information and expanding product sales in an era that preceded specialized market research and the domination of advertising companies. industrial production became widespread over the course of the A nineteenth century, the need arose for distribution networks to handle the burgeoning product volume.1 The faster sales increased, the more important it became to integrate, plan, and control distribution within the enterprise. As Heidrun Homburg has pointed out, the inter- nalization of the sales function served to secure, extend, and accelerate ROMAN ROSSFELD is Wissenschaftlicher Assistent (teaching and research associate) at the Forschungsstelle fiir Sozial- und Wirtschaftsgeschichte (Research Unit for Social and Economic History) at the University of Zurich in Switzerland. I am grateful to Hartmut Berghoff, Christof Dejung, and Ingo Kohler for their construc- tive criticism and valuable suggestions and to Fiona Sangster for translating this article into English. "Alfred D. Chandler, The Visible Hand: The Managerial Revolution in American Business (Cambridge, Mass., 1977), 287-314 and 382-414, and Scale and Scope: The Dynamics of In- dustrial Capitalism (Cambridge, Mass., 1990), 28-31.
    [Show full text]
  • Working Without Nets: Early Twentieth Century Mountain Women in Fiction 133
    Working Without Nets: Early Twentieth Century Mountain Women in Fiction 133 Gwen McNeill Ashburn Working Without Nets: Early Twentieth Century Mountain Women in Fiction by Gwen McNeill Ashburn She [Eliza] had grown triumphantly stronger after the diseases of the middle years. White, compact, a great deal heavier now than she had ever been, she performed daily tasks of drudgery in the maintenance of Dixieland, that would have floored a negro. She hardly ever got to bed before two o’clock in the morn- ing, and was up again before seven. —Thomas Wolfe Look Homeward, Angel Eugene Gant, the protagonist of Look Homeward, Angel, finds life difficult, blam- ing his mother, Eliza, whom he describes as demanding, insensitive, and cheap. Many readers, including my students, decide Eliza is an exact replica of Thomas Wolfe’s mother, Julia, owner and operator of The Old Kentucky Home. Each time I hear such an analysis I cringe. It is true that Julia Wolfe, as her fictional counterpart Eliza is portrayed in Look Homeward, Angel, was a parsimonious businesswoman who worked tirelessly in a boarding house she owned and operated. And it is true Thomas Wolfe—growing up amid the traveling salesmen, lonely widows, surreptitious sufferers of tuberculosis or other ailments, without a place to call his own—found life irritating, no matter how much material it provided for his later fiction. However, I have no sympathy for Eugene Gant, Thomas Wolfe, or others who are eager to depict negatives in memoirs or fiction with their hard-working mothers. Through her labors—she was most likely uncheerful at times and worried about finances—Julia Wolfe accommodated travel- ers and boarders who needed a reasonable place to stay, provided thousands of meals to her paying guests, borrowed money to buy property, paid her bills, and sent her youngest, self-centered child to university and graduate school.
    [Show full text]
  • “Soap and Hope”: Direct Sales and the Culture of Work and Capitalism in Postwar America
    “Soap and Hope”: Direct Sales and the Culture of Work and Capitalism in Postwar America By Jessica Kay Burch Dissertation Submitted to the Faculty of the Graduate School of Vanderbilt University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY in History August, 2015 Nashville, Tennessee Approved: Sarah Igo, Ph.D. Katherine Crawford, Ph.D. Gary Gerstle, Ph.D. Paul Kramer, Ph.D. Bethany Moreton, Ph.D. Copyright © 2015 by Jessica Kay Burch All Rights Reserved ACKNOWLEDGEMENTS I wish to express my gratitude, first and foremost, to Sarah Igo. Sarah guided this project from its inception. She read countless drafts, gave generous and insightful comments, and always offered to do more. Over the past six years, Sarah was a constant source of encouragement, advice, and support. She is a model teacher, mentor, scholar, and human being. It has been my great privilege to work with and learn from her. I am grateful to the members of the dissertation committee: Sarah Igo, Gary Gerstle, Katherine Crawford, Paul Kramer, and Bethany Moreton. Inspiring teachers and scholars all, they pushed me to see the big picture and to make arguments that matter. Thank you to the History Department at Vanderbilt University, where I benefited from seminars with Sarah Igo, Gary Gerstle, Paul Kramer, Dan Usner, Leor Halevi, Jim Epstein, and Michael Bess. Gary Gerstle, who once warned that his Modern U.S. History seminar would be the nadir of my graduate experience, was especially influential in shaping me as an historian. My work has benefitted from the generosity of many institutions: the Smithsonian Institution; the Bentley Historical Library at the University of Michigan; the John W.
    [Show full text]
  • Pension Plans for Outside Salesmen Dissertation
    PENSION PLANS FOR OUTSIDE SALESMEN DISSERTATION Preaented In Partial Fulfillment of the Requirement* for the Degree Doctor of Philosophy in the Graduate School of The Ohio State Uhivarsity By PHILLIP MoVSY, A.B., I.A., M»B«A* The Ohio State Chivarsity 1054 Approved by s -- 1 * Advlser 1 TABLE OF CONTENTS Chapter Page Number 1 INTRODUCTION 1 Pensions as a sales management problem 1 Plan of this study 5 Cooperation of National Sales Executives, Inc* 6 The questionnaire survey 9 2 OUTSIDE SALESMEN AND THE PROBLEM OF AGE 15 Number of persons employed as outside salesmen 15 Age factors In sales work 19 Preference for older salesmen In some lines 20 Brief work experience of most salesmen on current Jobs 22 Influence of young "marginal" sales workers 26 Loss of capacity* courage and desire In later years 27 Resistance of salesmen to old-age planning 29 3 SCOPE OF PENSION COVERAGE IN THE UNITED STATES 31 What Is a private pension plan? 31 Growth of pension plans since 1942 32 Outside salesmen and the Social Security Act 37 Internal Revenue Act of 1942 42 Outside salesmen under emergency wage and salary controls 43 Decision of the National Labor Relations Board 44 II Chapter Page Number Forces indirectly stimulating the growth of pensions 47 Aging population 47 Shorter working life 48 Increasing maturity of men in management and marketing 49 Radiation of employee benefit plans 50 Values of pension plans to employers 51 4 MANAGEMENT PROBLEMS IN THE RETIREMENT OF OUTSIDE SALESMEN 52 Desire for special efforts and attitudes 52 Inability to apply
    [Show full text]
  • Effective Strategies for Defending Traveling Employee Claims
    EFFECTIVE STRATEGIES FOR DEFENDING TRAVELING EMPLOYEE CLAIMS Presented and Prepared by: Craig S. Young [email protected] Peoria, Illinois • 309.676.0400 Heyl, Royster, Voelker & Allen PEORIA • SPRINGFIELD • URBANA • ROCKFORD • EDWARDSVILLE • CHICAGO © 2014 Heyl, Royster, Voelker & Allen E-1 EFFECTIVE STRATEGIES FOR DEFENDING TRAVELING EMPLOYEE CLAIMS I. EFFECTIVE STRATEGIES FOR DEFENDING TRAVELING EMPLOYEE CLAIMS ...................................................................................................................................... E-3 II. THE SUPREME COURT SPEAKS IN VENTURE-NEWBERG .............................................................. E-7 III. PRACTICE POINTERS FOR DEFENDING AGAINST TRAVELING EMPLOYEE DOCTRINE ................................................................................................................................ E-8 A. Raise the Supreme Court’s decision in Venture-Newberg ............................................. E-8 B. Don’t Ever Raise the Traveling Employee Doctrine .......................................................... E-9 C. Limit Travel in the Workplace ................................................................................................... E-9 D. Don’t Accept All Activities as Reasonably Foreseeable .................................................. E-9 The cases and materials presented here are in summary and outline form. To be certain of their applicability and use for specific claims, we recommend the entire opinions and statutes be read and counsel consulted.
    [Show full text]