Disentangling of Spectra-Theory and Practice
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

QEMU Version 2.10.2 User Documentation I
QEMU version 2.10.2 User Documentation i Table of Contents 1 Introduction ::::::::::::::::::::::::::::::::::::: 1 1.1 Features :::::::::::::::::::::::::::::::::::::::::::::::::::::::: 1 2 QEMU PC System emulator ::::::::::::::::::: 2 2.1 Introduction :::::::::::::::::::::::::::::::::::::::::::::::::::: 2 2.2 Quick Start::::::::::::::::::::::::::::::::::::::::::::::::::::: 2 2.3 Invocation :::::::::::::::::::::::::::::::::::::::::::::::::::::: 3 2.3.1 Standard options :::::::::::::::::::::::::::::::::::::::::: 3 2.3.2 Block device options ::::::::::::::::::::::::::::::::::::::: 9 2.3.3 USB options:::::::::::::::::::::::::::::::::::::::::::::: 19 2.3.4 Display options ::::::::::::::::::::::::::::::::::::::::::: 19 2.3.5 i386 target only::::::::::::::::::::::::::::::::::::::::::: 26 2.3.6 Network options :::::::::::::::::::::::::::::::::::::::::: 27 2.3.7 Character device options:::::::::::::::::::::::::::::::::: 35 2.3.8 Device URL Syntax::::::::::::::::::::::::::::::::::::::: 39 2.3.9 Bluetooth(R) options ::::::::::::::::::::::::::::::::::::: 42 2.3.10 TPM device options ::::::::::::::::::::::::::::::::::::: 42 2.3.11 Linux/Multiboot boot specific ::::::::::::::::::::::::::: 43 2.3.12 Debug/Expert options ::::::::::::::::::::::::::::::::::: 44 2.3.13 Generic object creation :::::::::::::::::::::::::::::::::: 52 2.4 Keys in the graphical frontends :::::::::::::::::::::::::::::::: 58 2.5 Keys in the character backend multiplexer ::::::::::::::::::::: 58 2.6 QEMU Monitor ::::::::::::::::::::::::::::::::::::::::::::::: 59 2.6.1 Commands ::::::::::::::::::::::::::::::::::::::::::::::: -

Visual Double Star Measurements with an Alt-Azimuth Telescope
Vol. 4 No. 2 Spring 2008 Journal of Double Star Observations Page 59 Visual Double Star Measurements with an Alt-Azimuth Telescope Thomas G. Frey California Polytechnic State University San Luis Obispo, CA 93407 Abstract: An alt-az mounted Newtonian telescope was used to determine the separation and position angle of seven known and five neglected double stars. The problem of field rotation was solved by modifying the usual observing technique. Separation and position angle determinations are described, and the standard deviations and mean errors for these measurements are presented. The direction of future studies is outlined. techniques were accurate and precise, additional Introduction measurements on neglected double stars listed in the Professional astronomers have carried out visual Washington Double Star Catalogue were made. double star measurements for over 200 years. These scientists measured the separation between double Double Star Observation: Equatorial vs. stars in arc seconds, and the position angle in degrees Alt-Az Mounts that defined the orientation of pairs with respect to Most observers involved in double star measure- celestial north. Over time, the orbital motion of each ments, including Argyle (p.x) and Teague (p.112), star can create a change in the observed separation recommend the use of equatorial mounted telescopes. and position angle if the pair proves to be binary in Such telescopes have drive motors that are oriented so nature. A binary star revolves around a common the right ascension axis rotates around the north center of mass. celestial pole, canceling out the Earth’s rotation and Today’s amateur astronomers continue to evaluate the image in the eyepiece remains stationary. -
M17 CEN1.Pdf
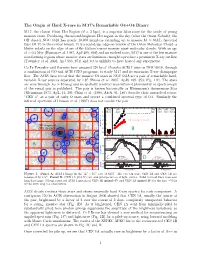
The Origin of Hard X-rays in M 17's Remarkable O4+O4 Binary M 17, the closest Giant H ii Region (d ≈ 2 kpc), is a superior laboratory for the study of young massive stars. Producing the second-brightest H ii region in the sky (after the Orion Nebula), the OB cluster NGC 6618 has nearly 10,000 members extending up to masses M ≈ 60M (spectral type O4 V) in the central binary. It is a scaled-up, edge-on version of the Orion Molecular Cloud: a blister nebula on the edge of one of the Galaxy's most massive giant molecular clouds. With an age of ∼ 0:5 Myr (Hanson et al. 1997, ApJ 489, 698) and no evolved stars, M 17 is one of the few massive star-forming regions whose massive stars are luminous enough to produce a prominent X-ray outflow (Townsley et al. 2003, ApJ 593, 874) and yet is unlikely to have hosted any supernovae. Co-I's Townsley and Garmire have amassed 320 ks of Chandra ACIS-I time on NGC 6618, through a combination of GO and ACIS GTO programs, to study M 17 and its enormous X-ray champagne flow. The ACIS data reveal that the massive O4 stars in NGC 6618 are a pair of remarkable hard, variable X-ray sources separated by 1:800 (Broos et al. 2007, ApJS 169, 353; Fig. 1A). The stars are seen through AV ≈ 10 mag and no spatially resolved near-infrared photometry or spectroscopy of the visual pair is published. The pair is known historically as Kleinmann's Anonymous Star (Kleinmann 1973, ApL, 14, 39); Chini et al. -

List of Easy Double Stars for Winter and Spring = Easy = Not Too Difficult = Difficult but Possible
List of Easy Double Stars for Winter and Spring = easy = not too difficult = difficult but possible 1. Sigma Cassiopeiae (STF 3049). 23 hr 59.0 min +55 deg 45 min This system is tight but very beautiful. Use a high magnification (150x or more). Primary: 5.2, yellow or white Seconary: 7.2 (3.0″), blue 2. Eta Cassiopeiae (Achird, STF 60). 00 hr 49.1 min +57 deg 49 min This is a multiple system with many stars, but I will restrict myself to the brightest one here. Primary: 3.5, yellow. Secondary: 7.4 (13.2″), purple or brown 3. 65 Piscium (STF 61). 00 hr 49.9 min +27 deg 43 min Primary: 6.3, yellow Secondary: 6.3 (4.1″), yellow 4. Psi-1 Piscium (STF 88). 01 hr 05.7 min +21 deg 28 min This double forms a T-shaped asterism with Psi-2, Psi-3 and Chi Piscium. Psi-1 is the uppermost of the four. Primary: 5.3, yellow or white Secondary: 5.5 (29.7), yellow or white 5. Zeta Piscium (STF 100). 01 hr 13.7 min +07 deg 35 min Primary: 5.2, white or yellow Secondary: 6.3, white or lilac (or blue) 6. Gamma Arietis (Mesarthim, STF 180). 01 hr 53.5 min +19 deg 18 min “The Ram’s Eyes” Primary: 4.5, white Secondary: 4.6 (7.5″), white 7. Lambda Arietis (H 5 12). 01 hr 57.9 min +23 deg 36 min Primary: 4.8, white or yellow Secondary: 6.7 (37.1″), silver-white or blue 8. -

Virtualization Technologies Overview Course: CS 490 by Mendel
Virtualization technologies overview Course: CS 490 by Mendel Rosenblum Name Can boot USB GUI Live 3D Snaps Live an OS on mem acceleration hot of migration another ory runnin disk alloc g partition ation system as guest Bochs partially partially Yes No Container s Cooperati Yes[1] Yes No No ve Linux (supporte d through X11 over networkin g) Denali DOSBox Partial (the Yes No No host OS can provide DOSBox services with USB devices) DOSEMU No No No FreeVPS GXemul No No Hercules Hyper-V iCore Yes Yes No Yes No Virtual Accounts Imperas Yes Yes Yes Yes OVP (Eclipse) Tools Integrity Yes No Yes Yes No Yes (HP-UX Virtual (Integrity guests only, Machines Virtual Linux and Machine Windows 2K3 Manager in near future) (add-on) Jail No Yes partially Yes No No No KVM Yes [3] Yes Yes [4] Yes Supported Yes [5] with VMGL [6] Linux- VServer LynxSec ure Mac-on- Yes Yes No No Linux Mac-on- No No Mac OpenVZ Yes Yes Yes Yes No Yes (using Xvnc and/or XDMCP) Oracle Yes Yes Yes Yes Yes VM (manage d by Oracle VM Manager) OVPsim Yes Yes Yes Yes (Eclipse) Padded Yes Yes Yes Cell for x86 (Green Hills Software) Padded Yes Yes Yes No Cell for PowerPC (Green Hills Software) Parallels Yes, if Boot Yes Yes Yes DirectX 9 Desktop Camp is and for Mac installed OpenGL 2.0 Parallels No Yes Yes No partially Workstati on PearPC POWER Yes Yes No Yes No Yes (on Hypervis POWER 6- or (PHYP) based systems, requires PowerVM Enterprise Licensing) QEMU Yes Yes Yes [4] Some code Yes done [7]; Also supported with VMGL [6] QEMU w/ Yes Yes Yes Some code Yes kqemu done [7]; Also module supported -

GTO Keypad Manual, V5.001
ASTRO-PHYSICS GTO KEYPAD Version v5.xxx Please read the manual even if you are familiar with previous keypad versions Flash RAM Updates Keypad Java updates can be accomplished through the Internet. Check our web site www.astro-physics.com/software-updates/ November 11, 2020 ASTRO-PHYSICS KEYPAD MANUAL FOR MACH2GTO Version 5.xxx November 11, 2020 ABOUT THIS MANUAL 4 REQUIREMENTS 5 What Mount Control Box Do I Need? 5 Can I Upgrade My Present Keypad? 5 GTO KEYPAD 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 STOP Button 6 <PREV and NEXT> Buttons 7 Number Buttons 7 GOTO Button 7 ± Button 7 MENU / ESC Button 7 RECAL and NEXT> Buttons Pressed Simultaneously 7 ENT Button 7 Retractable Hanger 7 Keypad Protector 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 512K Memory Boards 8 Cleaning Red Keypad Display 8 Temperature Ratings 8 Environmental Recommendation 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Set Up your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Time and Date 9 Set Up Your Mount in the Field 10 Polar Alignment 10 Mach2GTO Daytime Alignment Routine 10 KEYPAD START UP SEQUENCE FOR NEW SETUPS OR SETUP IN NEW LOCATION 11 Assemble Your Mount 11 Startup Sequence 11 Location 11 Select Existing Location 11 Set Up New Location 11 Date and Time 12 Additional Information 12 KEYPAD START UP SEQUENCE FOR MOUNTS USED AT THE SAME LOCATION WITHOUT A COMPUTER 13 KEYPAD START UP SEQUENCE FOR COMPUTER CONTROLLED MOUNTS 14 1 OBJECTS MENU – HAVE SOME FUN! -

Comparison of Platform Virtual Machines - Wikipedia
Comparison of platform virtual machines - Wikipedia... http://en.wikipedia.org/wiki/Comparison_of_platform... Comparison of platform virtual machines From Wikipedia, the free encyclopedia The table below compares basic information about platform virtual machine (VM) packages. Contents 1 General Information 2 More details 3 Features 4 Other emulators 5 See also 6 References 7 External links General Information Name Creator Host CPU Guest CPU Bochs Kevin Lawton any x86, AMD64 CHARON-AXP Stromasys x86 (64 bit) DEC Alphaserver CHARON-VAX Stromasys x86, IA-64 VAX x86, x86-64, SPARC (portable: Contai ners (al so 'Zones') Sun Microsystems (Same as host) not tied to hardware) Dan Aloni helped by other Cooperati ve Li nux x86[1] (Same as parent) developers (1) Denal i University of Washington x86 x86 Peter Veenstra and Sjoerd with DOSBox any x86 community help DOSEMU Community Project x86, AMD64 x86 1 of 15 10/26/2009 12:50 PM Comparison of platform virtual machines - Wikipedia... http://en.wikipedia.org/wiki/Comparison_of_platform... FreeVPS PSoft (http://www.FreeVPS.com) x86, AMD64 compatible ARM, MIPS, M88K GXemul Anders Gavare any PowerPC, SuperH Written by Roger Bowler, Hercul es currently maintained by Jay any z/Architecture Maynard x64 + hardware-assisted Hyper-V Microsoft virtualization (Intel VT or x64,x86 AMD-V) OR1K, MIPS32, ARC600/ARC700, A (can use all OVP OVP Imperas [1] [2] Imperas OVP Tool s x86 (http://www.imperas.com) (http://www.ovpworld compliant models, u can write own to pu OVP APIs) i Core Vi rtual Accounts iCore Software -
![Arxiv:2006.10868V2 [Astro-Ph.SR] 9 Apr 2021 Spain and Institut D’Estudis Espacials De Catalunya (IEEC), C/Gran Capit`A2-4, E-08034 2 Serenelli, Weiss, Aerts Et Al](https://docslib.b-cdn.net/cover/3592/arxiv-2006-10868v2-astro-ph-sr-9-apr-2021-spain-and-institut-d-estudis-espacials-de-catalunya-ieec-c-gran-capit-a2-4-e-08034-2-serenelli-weiss-aerts-et-al-1213592.webp)
Arxiv:2006.10868V2 [Astro-Ph.SR] 9 Apr 2021 Spain and Institut D’Estudis Espacials De Catalunya (IEEC), C/Gran Capit`A2-4, E-08034 2 Serenelli, Weiss, Aerts Et Al
Noname manuscript No. (will be inserted by the editor) Weighing stars from birth to death: mass determination methods across the HRD Aldo Serenelli · Achim Weiss · Conny Aerts · George C. Angelou · David Baroch · Nate Bastian · Paul G. Beck · Maria Bergemann · Joachim M. Bestenlehner · Ian Czekala · Nancy Elias-Rosa · Ana Escorza · Vincent Van Eylen · Diane K. Feuillet · Davide Gandolfi · Mark Gieles · L´eoGirardi · Yveline Lebreton · Nicolas Lodieu · Marie Martig · Marcelo M. Miller Bertolami · Joey S.G. Mombarg · Juan Carlos Morales · Andr´esMoya · Benard Nsamba · KreˇsimirPavlovski · May G. Pedersen · Ignasi Ribas · Fabian R.N. Schneider · Victor Silva Aguirre · Keivan G. Stassun · Eline Tolstoy · Pier-Emmanuel Tremblay · Konstanze Zwintz Received: date / Accepted: date A. Serenelli Institute of Space Sciences (ICE, CSIC), Carrer de Can Magrans S/N, Bellaterra, E- 08193, Spain and Institut d'Estudis Espacials de Catalunya (IEEC), Carrer Gran Capita 2, Barcelona, E-08034, Spain E-mail: [email protected] A. Weiss Max Planck Institute for Astrophysics, Karl Schwarzschild Str. 1, Garching bei M¨unchen, D-85741, Germany C. Aerts Institute of Astronomy, Department of Physics & Astronomy, KU Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium and Department of Astrophysics, IMAPP, Radboud University Nijmegen, Heyendaalseweg 135, 6525 AJ Nijmegen, the Netherlands G.C. Angelou Max Planck Institute for Astrophysics, Karl Schwarzschild Str. 1, Garching bei M¨unchen, D-85741, Germany D. Baroch J. C. Morales I. Ribas Institute of· Space Sciences· (ICE, CSIC), Carrer de Can Magrans S/N, Bellaterra, E-08193, arXiv:2006.10868v2 [astro-ph.SR] 9 Apr 2021 Spain and Institut d'Estudis Espacials de Catalunya (IEEC), C/Gran Capit`a2-4, E-08034 2 Serenelli, Weiss, Aerts et al. -

Double and Multiple Star Measurements in the Northern Sky with a 10” Newtonian and a Fast CCD Camera in 2006 Through 2009
Vol. 6 No. 3 July 1, 2010 Journal of Double Star Observations Page 180 Double and Multiple Star Measurements in the Northern Sky with a 10” Newtonian and a Fast CCD Camera in 2006 through 2009 Rainer Anton Altenholz/Kiel, Germany e-mail: rainer.anton”at”ki.comcity.de Abstract: Using a 10” Newtonian and a fast CCD camera, recordings of double and multiple stars were made at high frame rates with a notebook computer. From superpositions of “lucky images”, measurements of 139 systems were obtained and compared with literature data. B/w and color images of some noteworthy systems are also presented. mented double stars, as will be described in the next Introduction section. Generally, I used a red filter to cope with By using the technique of “lucky imaging”, seeing chromatic aberration of the Barlow lens, as well as to effects can strongly be reduced, and not only the reso- reduce the atmospheric spectrum. For systems with lution of a given telescope can be pushed to its limits, pronounced color contrast, I also made recordings but also the accuracy of position measurements can be with near-IR, green and blue filters in order to pro- better than this by about one order of magnitude. This duce composite images. This setup was the same as I has already been demonstrated in earlier papers in used with telescopes under the southern sky, and as I this journal [1-3]. Standard deviations of separation have described previously [1-3]. Exposure times varied measurements of less than +/- 0.05 msec were rou- between 0.5 msec and 100 msec, depending on the tinely obtained with telescopes of 40 or 50 cm aper- star brightness, and on the seeing. -

LIFE Packages
LIFE packages Index Office automation Desktop Internet Server Web developpement Tele centers Emulation Health centers Graphics High Schools Utilities Teachers Multimedia Tertiary schools Programming Database Games Documentation Internet - Firefox - Browser - Epiphany - Nautilus - Ftp client - gFTP - Evolution - Mail client - Thunderbird - Internet messaging - Gaim - Gaim - IRC - XChat - Gaim - VoIP - Skype - Videomeeting - Gnome meeting - GnomeBittorent - P2P - aMule - Firefox - Download manager - d4x - Telnet - Telnet Web developpement - Quanta - Bluefish - HTML editor - Nvu - Any text editor - HTML galerie - Album - Web server - XAMPP - Collaborative publishing system - Spip Desktop - Gnome - Desktop - Kde - Xfce Graphics - Advanced image editor - The Gimp - KolourPaint - Simple image editor - gPaint - TuxPaint - CinePaint - Video editor - Kino - OpenOffice Draw - Vector vraphics editor - Inkscape - Dia - Diagram editor - Kivio - Electrical CAD - Electric - 3D modeller/render - Blender - CAD system - QCad Utilities - Calculator - gCalcTool - gEdit - gxEdit - Text editor - eMacs21 - Leafpad - Application finder - Xfce4-appfinder - Desktop search tool - Beagle - File explorer - Nautilus -Archive manager - File-Roller - Nautilus CD Burner - CD burner - K3B - GnomeBaker - Synaptic - System updates - apt-get - IPtables - Firewall - FireStarter - BackupPC - Backup - Amanda - gnome-terminal - Terminal - xTerm - xTerminal - Scanner - Xsane - Partition editor - gParted - Making image of disks - Partitimage - Mirroring over network - UDP Cast -

Supernova Star Maps
Supernova Star Maps Which Stars in the Night Sky Will Go Su pernova? About the Activity Allow visitors to experience finding stars in the night sky that will eventually go supernova. Topics Covered Observation of stars that will one day go supernova Materials Needed • Copies of this month's Star Map for your visitors- print the Supernova Information Sheet on the back. • (Optional) Telescopes A S A Participants N t i d Activities are appropriate for families Cre with children over the age of 9, the general public, and school groups ages 9 and up. Any number of visitors may participate. Location and Timing This activity is perfect for a star party outdoors and can take a few minutes, up to 20 minutes, depending on the Included in This Packet Page length of the discussion about the Detailed Activity Description 2 questions on the Supernova Helpful Hints 5 Information Sheet. Discussion can start Supernova Information Sheet 6 while it is still light. Star Maps handouts 7 Background Information There is an Excel spreadsheet on the Supernova Star Maps Resource Page that lists all these stars with all their particulars. Search for Supernova Star Maps here: http://nightsky.jpl.nasa.gov/download-search.cfm © 2008 Astronomical Society of the Pacific www.astrosociety.org Copies for educational purposes are permitted. Additional astronomy activities can be found here: http://nightsky.jpl.nasa.gov Star Maps: Stars likely to go Supernova! Leader’s Role Participants’ Role (Anticipated) Materials: Star Map with Supernova Information sheet on back Objective: Allow visitors to experience finding stars in the night sky that will eventually go supernova. -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae