A New Interpretation of Ptolemy's Coordinates
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Simulation of the Potential Impacts of Projected Climate Change on Streamflow in the Vakhsh River Basin in Central Asia Under CMIP5 RCP Scenarios
water Article Simulation of the Potential Impacts of Projected Climate Change on Streamflow in the Vakhsh River Basin in Central Asia under CMIP5 RCP Scenarios Aminjon Gulakhmadov 1,2,3,4 , Xi Chen 1,2,*, Nekruz Gulahmadov 1,3,5, Tie Liu 1 , Muhammad Naveed Anjum 6 and Muhammad Rizwan 5,7 1 State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China; [email protected] (A.G.); [email protected] (N.G.); [email protected] (T.L.) 2 Research Center for Ecology and Environment of Central Asia, Chinese Academy of Sciences, Urumqi 830011, China 3 Institute of Water Problems, Hydropower and Ecology of the Academy of Sciences of the Republic of Tajikistan, Dushanbe 734042, Tajikistan 4 Ministry of Energy and Water Resources of the Republic of Tajikistan, Dushanbe 734064, Tajikistan 5 University of Chinese Academy of Sciences, Beijing 100049, China; [email protected] 6 Department of Land and Water Conservation Engineering, Faculty of Agricultural Engineering and Technology, Pir Mehr Ali Shah Arid Agriculture University Rawalpindi, Rawalpindi 46000, Pakistan; [email protected] 7 Key Laboratory of Remote Sensing and Geospatial Science, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China * Correspondence: [email protected]; Tel.: +86-136-0992-3012 Received: 1 April 2020; Accepted: 15 May 2020; Published: 17 May 2020 Abstract: Millions of people in Uzbekistan, Turkmenistan, Tajikistan, and Kyrgyzstan are dependent on the freshwater supply of the Vakhsh River system. Sustainable management of the water resources of the Vakhsh River Basin (VRB) requires comprehensive assessment regarding future climate change and its implications for streamflow. -

The Silk Roads: an ICOMOS Thematic Study
The Silk Roads: an ICOMOS Thematic Study by Tim Williams on behalf of ICOMOS 2014 The Silk Roads An ICOMOS Thematic Study by Tim Williams on behalf of ICOMOS 2014 International Council of Monuments and Sites 11 rue du Séminaire de Conflans 94220 Charenton-le-Pont FRANCE ISBN 978-2-918086-12-3 © ICOMOS All rights reserved Contents STATES PARTIES COVERED BY THIS STUDY ......................................................................... X ACKNOWLEDGEMENTS ..................................................................................................... XI 1 CONTEXT FOR THIS THEMATIC STUDY ........................................................................ 1 1.1 The purpose of the study ......................................................................................................... 1 1.2 Background to this study ......................................................................................................... 2 1.2.1 Global Strategy ................................................................................................................................ 2 1.2.2 Cultural routes ................................................................................................................................. 2 1.2.3 Serial transnational World Heritage nominations of the Silk Roads .................................................. 3 1.2.4 Ittingen expert meeting 2010 ........................................................................................................... 3 2 THE SILK ROADS: BACKGROUND, DEFINITIONS -

Ecosystem Service Assessment of the Ili Delta, Kazakhstan Niels Thevs
Ecosystem service assessment of the Ili Delta, Kazakhstan Niels Thevs, Volker Beckmann, Sabir Nurtazin, Ruslan Salmuzauli, Azim Baibaysov, Altyn Akimalieva, Elisabeth A. A. Baranoeski, Thea L. Schäpe, Helena Röttgers, Nikita Tychkov 1. Territorial and geographical location Ili Delta, Kazakhstan Almatinskaya Oblast (province), Bakanas Rayon (county) The Ili Delta is part of the Ramsar Site Ile River Delta and South Lake Balkhash Ramsar Site 2. Natural and geographic data Basic geographical data: location between 45° N and 46° N as well as 74° E and 75.5° E. Fig. 1: Map of the Ili-Balkhash Basin (Imentai et al., 2015). Natural areas: The Ramsar Site Ile River Delta and South Lake Balkhash Ramsar Site comprises wetlands and meadow vegetation (the modern delta), ancient river terraces that now harbour Saxaul and Tamarx shrub vegetation, and the southern coast line of the western part of Lake Balkhash. Most ecosystem services can be attributed to the wetlands and meadow vegetation. Therefore, this study focusses on the modern delta with its wetlands and meadows. During this study, a land cover map was created through classification of Rapid Eye Satellite images from the year 2014. The land cover classes relevant for this study were: water bodies in the delta, dense reed (total vegetation more than 70%), and open reed and shrub vegetation (vegetation cover of reed 20- 70% and vegetation cover of shrubs and trees more than 70%). The land cover class dense reed was further split into submerged dense reed and non-submerged dense reed by applying a threshold to the short wave infrared channel of a Landsat satellite image from 4 April 2015. -

INDIVIDUAL CONSULTANT PROCUREMENT NOTICE Date: July 30, 2021 Reference Number: IC-2021-080
DocuSign Envelope ID: BB6EA17B-538D-4D65-97EA-6E8871B739CA INDIVIDUAL CONSULTANT PROCUREMENT NOTICE Date: July 30, 2021 Reference Number: IC-2021-080 Country: Republic of Kazakhstan Description of the Leader of the expert group for the development of the Scientific Background assignment: report and Feasibility Study for the creation of 5 new PAs1 and a program for monitoring the biodiversity of 5 pilot PAs2 Project name: UNDP-GEF Project "Conservation and Sustainable Management of Key Globally Important Ecosystems for Multiple Benefits", 00101043 Period of August 2021 - December 2022 (250 working days within 17 months) assignment/services: Contract Modality: Individual contractor (IC) Any request for clarification must be sent by standard electronic communication to the e-mail [email protected] and in e-mail subject please indicate Request_Ref.2021-080. 1. BACKGROUND The total forest area in Kazakhstan is about 12.6 million hectares, which makes it one of the richest in forest countries in Eurasia, despite the low level of forest cover, which is only 4.6%. Approximately 95% of the forests (wooded areas) in Kazakhstan are managed by 123 forestry administrations, which are controlled by regional governments (akimats). There are three main types of forest ecosystems in Kazakhstan: alpine mountain forests, tugai (southern coastal) forests and saxaul landscapes (desert and semi-desert shrubs). Since 2018, the GEF-UNDP project "Conservation and sustainable management of key globally significant ecosystems for obtaining various benefits" (hereinafter referred to as the project) has been implemented on the territory of the republic. The project strategy is to holistically address the conservation and sustainable use of forest ecosystems in Kazakhstan, through management approaches including both protected areas and sustainable use of associated HCVF landscapes (maps of the project areas are presented in Appendices 4, 5, 6 to the Terms of Reference). -

“Kashgar City Circle” Industry Development in the Contest of the Silk Road Economic Belt
E3S Web of Conferences 235, 02023 (2021) https://doi.org/10.1051/e3sconf/202123502023 NETID 2020 A Study on “Kashgar City Circle” Industry Development in the Contest of the Silk Road Economic Belt Pan Jie1,a, Bai Xiao*2,b(Corresponding Author) 1 Faculty of Transportation and Management, Xinjiang Vocational and Technical College of Communications, Urumqi, Xinjiang, China 2 Postdoctoral Innovation Practice Base, Xinjiang Vocational and Technical College of Communications, Urumqi, Xinjiang, China Abstract. Kashgar City Circle is an important node of the new The Silk Road economic belt.Kashgar City Circle will serve as a new economic growth pole in the western region and will promote the rapid development of regional economy.The development of industry is an important driving force for regional economic development.This paper analyzes the four indicators of total output value,output value growth rate,employed population and labor productivity of the 18 industrial sectors of Kashgar City Circle from 2012 to 2016.Combined with the opportunities brought by the Silk Road economic belt background to the development of the Kashgar City Circle industry,this paper puts forward the current policy recommendations for the development of the Kashgar City Circle industry. research on the adjustment and optimization of industrial 1 Introduction structure [6-10],the current economic development situation[11-12],the impact of fixed asset investment on Kashgar is the traffic hub of the ancient The Silk Road, the industrial structure change[13-14].However, based on the traffic hub of the new The Silk Road economic belt, and a background of The Silk Road economic belt, there are major channel for trade with neighboring countries. -
CBD Strategy and Action Plan
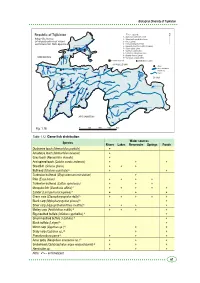
Biological Diversity of Tajikistan Republic of Tajikistan The Legend: 1 - Acipenser nudiventris Lovet 2 - Salmo trutta morfa fario Linne ya 3 - A.a.a. (Linne) ar rd Sy 4 - Ctenopharyngodon idella Kayrakkum reservoir 5 - Hypophthalmichtus molitrix (Valenea) Khujand 6 - Silurus glanis Linne 7 - Cyprinus carpio Linne a r a 8 - Lucioperca lucioperea Linne f s Dagano-Say I 9 - Abramis brama (Linne) reservoir UZBEKISTAN 10 -Carassus auratus gibilio Katasay reservoir economical pond distribution location KYRGYZSTAN cities Zeravshan lakes and water reservoirs Yagnob rivers Muksu ob Iskanderkul Lake Surkh o CHINA b r Karakul Lake o S b gou o in h l z ik r b e a O b V y u k Dushanbe o ir K Rangul Lake o rv Shorkul Lake e P ch z a n e n a r j V ek em Nur gul Murg u az ab s Y h k a Y u ng Sarez Lake s l ta i r a u iz s B ir K Kulyab o T Kurgan-Tube n a g i n r Gunt i Yashilkul Lake f h a s K h Khorog k a Zorkul Lake V Turumtaikul Lake ra P a an d j kh Sha A AFGHANISTAN m u da rya nj a P Fig. 1.16. 0 50 100 150 Km Table 1.12. Game fish distribution Water sources Species Rivers Lakes Reservoirs Springs Ponds Dushanbe loach (Nemachilus pardalis) + Amudarya loach (Nemachilus oxianus) + Gray loach (Nemachilus dorsalis) + Aral spined loach (Cobitis aurata aralensis) + + + Sheatfish (Sclurus glanis) + + + Bullhead (Ictalurus punctata) А + + Turkestan bullhead (Glyptosternum reticulatum) + Pike (Esox lucius) + + + + Turkestan bullhead (Cottus spinolosus) + + + Mosquito fish (Gambusia affinis) А + + + + + Zander (Lucioperca lucioperea) А + + + Grass carp (Ctenopharyngodon della) А + + + + + Black carp (Mylopharyngodon piceus) А + Silver carp (Hypophthalmichthus molitrix) А + + + + Motley carp (Aristichthus nobilis) А + + + + Big-mouthed buffalo (Ictiobus cyprinellus) А + Small-mouthed buffalo (I.bufalus) А + Black buffalo (I.niger) А + Mirror carp (Cyprinus sp.) А + + Scaly carp (Cyprinus sp.) А + + Pseudorasbora parva А + + + Amur goby (Neogobius amurensis sp.) А + + + Snakehead (Ophiocephalus argus warpachowski) А + + + Hemiculter sp. -

Water Resources Lifeblood of the Region
Water Resources Lifeblood of the Region 68 Central Asia Atlas of Natural Resources ater has long been the fundamental helped the region flourish; on the other, water, concern of Central Asia’s air, land, and biodiversity have been degraded. peoples. Few parts of the region are naturally water endowed, In this chapter, major river basins, inland seas, Wand it is unevenly distributed geographically. lakes, and reservoirs of Central Asia are presented. This scarcity has caused people to adapt in both The substantial economic and ecological benefits positive and negative ways. Vast power projects they provide are described, along with the threats and irrigation schemes have diverted most of facing them—and consequently the threats the water flow, transforming terrain, ecology, facing the economies and ecology of the country and even climate. On the one hand, powerful themselves—as a result of human activities. electrical grids and rich agricultural areas have The Amu Darya River in Karakalpakstan, Uzbekistan, with a canal (left) taking water to irrigate cotton fields.Upper right: Irrigation lifeline, Dostyk main canal in Makktaaral Rayon in South Kasakhstan Oblast, Kazakhstan. Lower right: The Charyn River in the Balkhash Lake basin, Kazakhstan. Water Resources 69 55°0'E 75°0'E 70 1:10 000 000 Central AsiaAtlas ofNaturalResources Major River Basins in Central Asia 200100 0 200 N Kilometers RUSSIAN FEDERATION 50°0'N Irty sh im 50°0'N Ish ASTANA N ura a b m Lake Zaisan E U r a KAZAKHSTAN l u s y r a S Lake Balkhash PEOPLE’S REPUBLIC Ili OF CHINA Chui Aral Sea National capital 1 International boundary S y r D a r Rivers and canals y a River basins Lake Caspian Sea BISHKEK Issyk-Kul Amu Darya UZBEKISTAN Balkhash-Alakol 40°0'N ryn KYRGYZ Na Ob-Irtysh TASHKENT REPUBLIC Syr Darya 40°0'N Ural 1 Chui-Talas AZERBAIJAN 2 Zarafshan TURKMENISTAN 2 Boundaries are not necessarily authoritative. -

Energy Efficiency, Denmark Singapore Access to Energy, Estonia South Africa Demand Side Finland Thailand Management and France Much More
Kazakhstan Energy Profile INTERNATIONAL ENERGY AGENCY The IEA examines IEA member IEA association the full spectrum countries: countries: of energy issues including oil, gas Australia Brazil and coal supply and Austria China demand, renewable Belgium India energy technologies, Canada Indonesia electricity markets, Czech Republic Morocco energy efficiency, Denmark Singapore access to energy, Estonia South Africa demand side Finland Thailand management and France much more. Through Germany its work, the IEA Greece advocates policies Hungary that will enhance Ireland the reliability, Italy affordability and Japan sustainability of Korea energy in its Luxembourg 30 member Mexico countries, Netherlands 8 association New Zealand countries and Norway beyond. Poland Portugal Slovak Republic Spain Sweden Switzerland Turkey United Kingdom United States The European Commission also participates in the work of the IEA Please note that this publication is subject to specific restrictions that limit its use and distribution. The terms and conditions are available online at www.iea.org/t&c/ Source: IEA. All rights reserved. International Energy Agency Website: www.iea.org Kazakhstan Table of contents Country overview Table of contents Kazakhstan Energy Profile ...................................................................................................... 2 Country overview ....................................................................................................................... 2 Key energy data ........................................................................................................................ -

The Geodynamics of the Pamir–Punjab Syntaxis V
ISSN 00168521, Geotectonics, 2013, Vol. 47, No. 1, pp. 31–51. © Pleiades Publishing, Inc., 2013. Original Russian Text © V.S. Burtman, 2013, published in Geotektonika, 2013, Vol. 47, No. 1, pp. 36–58. The Geodynamics of the Pamir–Punjab Syntaxis V. S. Burtman Geological Institute, Russian Academy of Sciences, Pyzhevskii per. 7, Moscow, 119017 Russia email: [email protected] Received December 19, 2011 Abstract—The collision of Hindustan with Eurasia in the Oligocene–early Miocene resulted in the rear rangement of the convective system in the upper mantle of the Pamir–Karakoram margin of the Eurasian Plate with subduction of the Hindustan continental lithosphere beneath this margin. The Pamir–Punjab syn taxis was formed in the Miocene as a giant horizontal extrusion (protrusion). Extensive nappes developed in the southern and central Pamirs along with deformation of its outer zone. The Pamir–Punjab syntaxis con tinued to form in the Pliocene–Quaternary when the deformed Pamirs, which propagated northward, were being transformed into a giant allochthon. A fold–nappe system was formed in the outer zone of the Pamirs at the front of this allochthon. A geodynamic model of syntaxis formation is proposed here. DOI: 10.1134/S0016852113010020 INTRODUCTION Mujan, BandiTurkestan, Andarab, and Albruz– The tectonic processes that occur in the Pamir– Mormul faults (Fig. 1). Punjab syntaxis of the Alpine–Himalayan Foldbelt The Pamir arc is more compressed as compared and at the boundary of this syntaxis with the Tien Shan with the Hindu Kush–Karakoram arc. Disharmony of have attracted the attention of researchers for many these arcs arose in the western part of the syntaxis due years [2, 7–9, 13, 15, 28]. -

Central Asian Rivers Under Climate Change: Impacts Assessment in Eight Representative Catchments
A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Didovets, Iulii et al. Article — Published Version Central Asian rivers under climate change: Impacts assessment in eight representative catchments Journal of Hydrology: Regional Studies Provided in Cooperation with: Leibniz Institute of Agricultural Development in Transition Economies (IAMO), Halle (Saale) Suggested Citation: Didovets, Iulii et al. (2021) : Central Asian rivers under climate change: Impacts assessment in eight representative catchments, Journal of Hydrology: Regional Studies, ISSN 2214-5818, Elsevier, Amsterdam, Vol. 34, Iss. (Article No.:) 100779, http://dx.doi.org/10.1016/j.ejrh.2021.100779 This Version is available at: http://hdl.handle.net/10419/229441 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur -

Natural Recreation Potential of the West Kazakhstan Region of the Republic of Kazakhstan
GeoJournal of Tourism and Geosites Year XIII, vol. 32, no. 4, 2020, p.1355-1361 ISSN 2065-1198, E-ISSN 2065-0817 DOI 10.30892/gtg.32424-580 NATURAL RECREATION POTENTIAL OF THE WEST KAZAKHSTAN REGION OF THE REPUBLIC OF KAZAKHSTAN Bibigul CHASHINA L.N. Gumilyov Eurasian National University, Faculty of Natural Sciences, Satpayev Str., 2, 010008 Nur-Sultan, Republic of Kazakhstan, e-mail: [email protected] Nurgul RAMAZANOVA L.N. Gumilyov Eurasian National University, Faculty of Natural Sciences, Satpayev Str., 2, 010008 Nur-Sultan, Republic of Kazakhstan, e-mail: [email protected] Emin ATASOY Bursa Uludag University, 6059, Gorukle, Bursa, Turkye, e-mail: [email protected] Zharas BERDENOV* L.N. Gumilyov Eurasian National University, Faculty of Natural Sciences, Satpayev Str., 2, 010008 Nur-Sultan, Republic of Kazakhstan, e-mail: [email protected] Dorina Camelia ILIEȘ University of Oradea, Faculty of Geography, Tourism and Sport, Department of Geography, Tourism and Territorial Planning, Oradea, Romania, e-mail: [email protected] Citation: Chashina, B., Ramazanova, N., Atasoy, E., Berdenov, Zh., & Ilieș, D.C. (2020). NATURAL RECREATION POTENTIAL OF THE WEST KAZAKHSTAN REGION OF THE REPUBLIC OF KAZAKHSTAN. GeoJournal of Tourism and Geosites, 32(4), 1355–1361. https://doi.org/10.30892/gtg.32424-580 Abstract: This article is an attempt to assess the natural and recreational potential of the West Kazakhstan region. This technique consists of different stages: assessment of the territory concerning the recreational potential, according to the physical and geographi cal conditions; determination of administrative districts (units) within each of the recreational development zones; inventory of specially protected natural areas.The main criterion for the quantitative assessment was the presence of specially protected natural areas, their number and occupied area. -

From Uyghurs to Kashgaris (And Back?) : Migration and Cross-Border Interactions Between Xinjiang and Pakistan
11 Alessandro Rippa 11 From Uyghurs to Kashgaris (and Martin Sökefeld Martin back?) Migration and cross-border interactions between Xinjiang and Pakistan Thomas Reinhardt, München 2014 ISBN 978-3-945254-04-2 7 STUDIEN AUS DEM MÜNCHNER INSTITUT FÜR ETHNOLOGIE, FÜR Band INSTITUT STUDIEN DEM AUS MÜNCHNER Vol MUNICH, LMU ANTHROPOLOGY, CULTURAL AND SOCIAL IN PAPERS WORKING Heidemann, Frank Dürr, Eveline Herausgeber: Abstract: China and Pakistan share a common border, formally established in 1963, and a close friendship which, to a certain extent, is a direct consequence of that agree- ment. Somewhat surprisingly the two countries managed to maintain - and even improve - their friendly ties in spite of several events which might have undermined the basis of their friendship. Particularly, since September 11, 2001, China has con- demned various incidents in its Muslim province of Xinjiang as connected to the global jihad, often holding Pakistan-based Uyghur militants responsible and accus- ing Islamabad of not doing enough to prevent violence from spreading into Chinese territory. Within a scenario of growing insecurity for the whole region, in this paper I show how China’s influence in Pakistan goes well beyond the mere government- to-government level. Particularly, I address the hitherto unstudied case of the Uy- ghur community of Pakistan, the Kashgaris, a group of migrants who left Xinjiang over the course of the last century. This paper, based on four months of fieldwork in Pakistan, aims principally at offering an overview of the history and current situa- tion of the Uyghur community of Pakistan. It thus first examines the migration of the Uyghur families to Pakistan according to several interviews with elder members of the community.