Signatures of the Martian Rotation Parameters in the Doppler and Range Observables
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data
remote sensing Article Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data Justyna Sliwi´ ´nska 1,* , Małgorzata Wi ´nska 2 and Jolanta Nastula 1 1 Space Research Centre, Polish Academy of Sciences, 00-716 Warsaw, Poland; [email protected] 2 Faculty of Civil Engineering, Warsaw University of Technology, 00-637 Warsaw, Poland; [email protected] * Correspondence: [email protected] Received: 18 September 2020; Accepted: 22 October 2020; Published: 23 October 2020 Abstract: The Gravity Recovery and Climate Experiment (GRACE) mission has provided global observations of temporal variations in the gravity field resulting from mass redistribution at the surface and within the Earth for the period 2002–2017. Although GRACE satellites are not able to realistically detect the second zonal parameter (DC20) of geopotential associated with the flattening of the Earth, they can accurately determine variations in degree-2 order-1 (DC21, DS21) coefficients that are proportional to variations in polar motion. Therefore, GRACE measurements are commonly exploited to interpret polar motion changes due to variations in the global mass redistribution, especially in the continental hydrosphere and cryosphere. Such impacts are usually examined by computing the so-called hydrological polar motion excitation (HAM) and cryospheric polar motion excitation (CAM), often analyzed together as HAM/CAM. The great success of the GRACE mission and the scientific robustness of its data contributed to the launch of its successor, GRACE Follow-On (GRACE-FO), which began in May 2018 and continues to the present. This study presents the first estimates of HAM/CAM computed from GRACE-FO data provided by three data centers: Center for Space Research (CSR), Jet Propulsion Laboratory (JPL), and GeoForschungsZentrum (GFZ). -

The Periglacial Landscape of Utopia Planitia; Geologic Evidence for Recent Climate Change on Mars
Western University Scholarship@Western Electronic Thesis and Dissertation Repository 1-23-2013 12:00 AM The Periglacial Landscape Of Utopia Planitia; Geologic Evidence For Recent Climate Change On Mars. Mary C. Kerrigan The University of Western Ontario Supervisor Dr. Marco Van De Wiel The University of Western Ontario Joint Supervisor Dr. Gordon R Osinski The University of Western Ontario Graduate Program in Geography A thesis submitted in partial fulfillment of the equirr ements for the degree in Master of Science © Mary C. Kerrigan 2013 Follow this and additional works at: https://ir.lib.uwo.ca/etd Part of the Climate Commons, Geology Commons, Geomorphology Commons, and the Physical and Environmental Geography Commons Recommended Citation Kerrigan, Mary C., "The Periglacial Landscape Of Utopia Planitia; Geologic Evidence For Recent Climate Change On Mars." (2013). Electronic Thesis and Dissertation Repository. 1101. https://ir.lib.uwo.ca/etd/1101 This Dissertation/Thesis is brought to you for free and open access by Scholarship@Western. It has been accepted for inclusion in Electronic Thesis and Dissertation Repository by an authorized administrator of Scholarship@Western. For more information, please contact [email protected]. THE PERIGLACIAL LANDSCAPE OF UTOPIA PLANITIA; GEOLOGIC EVIDENCE FOR RECENT CLIMATE CHANGE ON MARS by Mary C. Kerrigan Graduate Program in Geography A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science The School of Graduate and Postdoctoral Studies The University of Western Ontario London, Ontario, Canada © Mary C. Kerrigan 2013 ii THE UNIVERSITY OF WESTERN ONTARIO School of Graduate and Postdoctoral Studies CERTIFICATE OF EXAMINATION Joint Supervisor Examiners ______________________________ Dr. -

Pre-Mission Insights on the Interior of Mars Suzanne E
Pre-mission InSights on the Interior of Mars Suzanne E. Smrekar, Philippe Lognonné, Tilman Spohn, W. Bruce Banerdt, Doris Breuer, Ulrich Christensen, Véronique Dehant, Mélanie Drilleau, William Folkner, Nobuaki Fuji, et al. To cite this version: Suzanne E. Smrekar, Philippe Lognonné, Tilman Spohn, W. Bruce Banerdt, Doris Breuer, et al.. Pre-mission InSights on the Interior of Mars. Space Science Reviews, Springer Verlag, 2019, 215 (1), pp.1-72. 10.1007/s11214-018-0563-9. hal-01990798 HAL Id: hal-01990798 https://hal.archives-ouvertes.fr/hal-01990798 Submitted on 23 Jan 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Open Archive Toulouse Archive Ouverte (OATAO ) OATAO is an open access repository that collects the wor of some Toulouse researchers and ma es it freely available over the web where possible. This is an author's version published in: https://oatao.univ-toulouse.fr/21690 Official URL : https://doi.org/10.1007/s11214-018-0563-9 To cite this version : Smrekar, Suzanne E. and Lognonné, Philippe and Spohn, Tilman ,... [et al.]. Pre-mission InSights on the Interior of Mars. (2019) Space Science Reviews, 215 (1). -

True Polar Wander: Linking Deep and Shallow Geodynamics to Hydro- and Bio-Spheric Hypotheses T
True Polar Wander: linking Deep and Shallow Geodynamics to Hydro- and Bio-Spheric Hypotheses T. D. Raub, Yale University, New Haven, CT, USA J. L. Kirschvink, California Institute of Technology, Pasadena, CA, USA D. A. D. Evans, Yale University, New Haven, CT, USA © 2007 Elsevier SV. All rights reserved. 5.14.1 Planetary Moment of Inertia and the Spin-Axis 565 5.14.2 Apparent Polar Wander (APW) = Plate motion +TPW 566 5.14.2.1 Different Information in Different Reference Frames 566 5.14.2.2 Type 0' TPW: Mass Redistribution at Clock to Millenial Timescales, of Inconsistent Sense 567 5.14.2.3 Type I TPW: Slow/Prolonged TPW 567 5.14.2.4 Type II TPW: Fast/Multiple/Oscillatory TPW: A Distinct Flavor of Inertial Interchange 569 5.14.2.5 Hypothesized Rapid or Prolonged TPW: Late Paleozoic-Mesozoic 569 5.14.2.6 Hypothesized Rapid or Prolonged TPW: 'Cryogenian'-Ediacaran-Cambrian-Early Paleozoic 571 5.14.2.7 Hypothesized Rapid or Prolonged TPW: Archean to Mesoproterozoic 572 5.14.3 Geodynamic and Geologic Effects and Inferences 572 5.14.3.1 Precision of TPW Magnitude and Rate Estimation 572 5.14.3.2 Physical Oceanographic Effects: Sea Level and Circulation 574 5.14.3.3 Chemical Oceanographic Effects: Carbon Oxidation and Burial 576 5..14.4 Critical Testing of Cryogenian-Cambrian TPW 579 5.14A1 Ediacaran-Cambrian TPW: 'Spinner Diagrams' in the TPW Reference Frame 579 5.14.4.2 Proof of Concept: Independent Reconstruction of Gondwanaland Using Spinner Diagrams 581 5.14.5 Summary: Major Unresolved Issues and Future Work 585 References 586 5.14.1 Planetary Moment of Inertia location ofEarth's daily rotation axis and/or by fluc and the Spin-Axis tuations in the spin rate ('length of day' anomalies). -

Earth Orientation Parameters from VLBI Determined with a Kalman Filter
Originally published as: Karbon, M., Soja, B., Nilsson, T., Deng, Z., Heinkelmann, R., Schuh, H. (2017): Earth orientation parameters from VLBI determined with a Kalman filter. ‐ Geodesy and Geodynamics, 8, 6, pp. 396— 407. DOI: http://doi.org/10.1016/j.geog.2017.05.006 Geodesy and Geodynamics 8 (2017) 396e407 Contents lists available at ScienceDirect Geodesy and Geodynamics journal homepages: www.keaipublishing.com/en/journals/geog; http://www.jgg09.com/jweb_ddcl_en/EN/volumn/home.shtml Earth orientation parameters from VLBI determined with a Kalman filter * Maria Karbon a, , Benedikt Soja b, Tobias Nilsson a, Zhiguo Deng a, Robert Heinkelmann a, Harald Schuh a, c a GFZ German Research Centre for Geosciences, Telegrafenberg A17, Potsdam, Germany b Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, USA c Technical University of Berlin, Strabe des 17. Juni 135, Berlin, Germany article info abstract Article history: This paper introduces the reader to our Kalman filter developed for geodetic VLBI (very long baseline Received 24 November 2016 interferometry) data analysis. The focus lies on the EOP (Earth Orientation Parameter) determination Received in revised form based on the Continuous VLBI Campaign 2014 (CONT14) data, but also earlier CONT campaigns are 23 May 2017 analyzed. For validation and comparison purposes we use EOP determined with the classical LSM Accepted 24 May 2017 (least squares method) estimated from the same VLBI data set as the Kalman solution with a daily Available online 6 September 2017 resolution. To gain higher resolved EOP from LSM we run solutions which yield hourly estimates for polar motion and dUT1 ¼ Universal Time (UT1) e Coordinated Universal Time (UTC). -
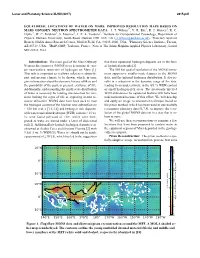
Equatorial Locations of Water on Mars: Improved Resolution Maps Based on Mars Odyssey Neutron Spectrometer Data
Lunar and Planetary Science XLVIII (2017) 2615.pdf EQUATORIAL LOCATIONS OF WATER ON MARS: IMPROVED RESOLUTION MAPS BASED ON MARS ODYSSEY NEUTRON SPECTROMETER DATA. J. T. Wilson1*, V. R. Eke1, R. J. Massey1, R. C. Elphic2, W. C. Feldman3, S. Maurice4, L. F. A. Teodoro2. 1Institute for Computational Cosmology, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK ([email protected]). 2Planetary Systems Branch, NASA Ames Research Center, Moffett Field, CA, 94035-1000, USA.3Planetary Science Institute, Tucson, AZ 85719, USA. 4IRAP-OMP, Toulouse, France Now at The Johns Hopkins Applied Physics Laboratory, Laurel MD 20723, USA Introduction: The main goal of the Mars Odyssey that these equatorial hydrogen deposits are in the form Neutron Spectrometer (MONS) is to determine the ma- of hydrated minerals [2]. jor near-surface reservoirs of hydrogen on Mars [1]. The 550 km spatial resolution of the MONS instru- This task is important as it allows inferences about the ment suppresses smaller-scale features in the MONS past and present climate to be drawn, which, in turn, data, and the inferred hydrogen distribution. It also re- give information about the dynamic history of Mars and sults in a reduction in the dynamic range of the data, the possibility of the past, or present, existence of life. leading to an underestimate in the wt. % WEH content Additionally, understanding the small-scale distribution of small hydrogen-rich areas. The previously inferred of water is necessary for landing site selection for mis- WEH abundances for equatorial features will have been sions looking for signs of life or exploring in-situ re- underestimated because of this effect. -

Constraining Ceres' Interior from Its Rotational Motion
A&A 535, A43 (2011) Astronomy DOI: 10.1051/0004-6361/201116563 & c ESO 2011 Astrophysics Constraining Ceres’ interior from its rotational motion N. Rambaux1,2, J. Castillo-Rogez3, V. Dehant4, and P. Kuchynka2,3 1 Université Pierre et Marie Curie, UPMC–Paris 06, France e-mail: [nicolas.rambaux;kuchynka]@imcce.fr 2 IMCCE, Observatoire de Paris, CNRS UMR 8028, 77 avenue Denfert-Rochereau, 75014 Paris, France 3 Jet Propulsion Laboratory, Caltech, Pasadena, USA e-mail: [email protected] 4 Royal Observatory of Belgium, 3 avenue Circulaire, 1180 Brussels, Belgium Received 24 January 2011 / Accepted 14 July 2011 ABSTRACT Context. Ceres is the most massive body of the asteroid belt and contains about 25 wt.% (weight percent) of water. Understanding its thermal evolution and assessing its current state are major goals of the Dawn mission. Constraints on its internal structure can be inferred from various types of observations. In particular, detailed knowledge of the rotational motion can help constrain the mass distribution inside the body, which in turn can lead to information about its geophysical history. Aims. We investigate the signature of internal processes on Ceres rotational motion and discuss future measurements that can possibly be performed by the spacecraft Dawn and will help to constrain Ceres’ internal structure. Methods. We compute the polar motion, precession-nutation, and length-of-day variations. We estimate the amplitudes of the rigid and non-rigid responses for these various motions for models of Ceres’ interior constrained by shape data and surface properties. Results. As a general result, the amplitudes of oscillations in the rotation appear to be small, and their determination from spaceborne techniques will be challenging. -

Present True Polar Wander in the Frame of the Geotectonic Reference System
1661-8726/08/030629-8 Swiss J. Geosci. 101 (2008) 629–636 DOI 10.1007/s00015-008-1284-y Birkhäuser Verlag, Basel, 2008 Present true polar wander in the frame of the Geotectonic Reference System NAZARIO PAVONI Key words: Geotectonic Reference System, polar wander, geodynamics, geotectonic bipolarity ABSTRACT The Mesozoic-Cenozoic evolution of the Earth’s lithosphere reveals a funda- mA which are responsible for the two geoid highs results in the long-standing mental hemispherical symmetry inherent in global tectonics. The symmetry stability of location of the geotectonic axis PA. The Earth’s rotation axis is is documented by the concurrent regular growth of the Pacific and African oriented perpendicularly to the PA axis. Owing to the extraordinary stabil- plates over the past 180 million years, and by the antipodal position of the two ity of the geotectonic axis, any change of orientation of the rotation axis, e.g. plates. The plates are centered on the equator, where center P of the Pacific induced by post-glacial rebound, occurs in such a way that the axis remains plate is located at 170° W/0° N, and center A of the African plate at 10° E/0° N. in the equatorial plane of the geotectonic system, i.e. in the 80° W/100° E P and A define a system of spherical coordinates, the Geotectonic Reference meridional plane. Observed present polar wander is directed towards 80° W System GRS, which shows a distinct relation to Cenozoic global tectonics. P (79.2 ± 0.2° W). This indicates that the present true polar wander is directed and A mark the poles of the geotectonic axis PA. -

The Origin of Fluvial Valleys and Early Geologic History, Aeolis Quadrangle
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 95, NO. Bll, PAGES 17,289-17,308, OCTOBER 10, 1990 The OriginOf FluvialValleys And EarlyGeologic History, Aeolis Quadrangle, Mars G. ROBERT BRAKENRIDGE Su•ficialProcesses Laboratory, Department of Geography,Dartmouth College, Hanover, New Hampshire In southernAeolis Quadrangle in easternMars, parallel slope valleys, flat-floored branching valleys, V- shapedbranching valleys, and flat-floored straight canyons dissect the heavilycratered plateau sequence. Associatedknife-like ridges are interpretedas fissure eruption vents, and thin, dark, stratiform outcrops are interpretedas exhumed igneous sills or lavaflows. Ridgedlava plains are also common but are not themselves modifiedby fluvialprocesses. I mapped 56 asymmetricscarps or ridgesthat are probable thrust faults. These faultsexhibit an orientationvector mean of N63ow + 11o (95% confidenceinterval), and they transect the lava plainsand the olderplateau sequence units. By comparison,the vectormean for the 264 valleysmapped is N48ow + 12o, witha largerdispersion about the mean. The similar orientations displayed by thrustfault and valley axessuggest that valley locationsare partlycontrolled by preexistingthrust faults and related fracture systems.Most valleysare alsoarranged orthogonally to, and alongthe perimeterof, the ridgedplains. A possiblemodel for valley developmentis: (1) freshlyoutgassed water became entombed as frost, snow, and ice within the crateredterrains during heavy bombardment and the accompanyingdeposition of impactejecta, volcanicash, -

The Ocean Pole Tide: a Review
Executive Committee Program Committee Fig 1. Attendee Profile by Research Interest Yun-Tai CHEN David HIGGITT, Chair Institute of Geophysics, The University of Nottingham China Earthquake Administration SE 19% Ningbo China AS 23% The Ocean Pole Tide: A ReviewBenjamin Fong CHAO Tetsuo NAKAZAWA, AS Section Institute of Earth Sciences, BG 2% Korea Meteorological Administration Academia Sinica ST 16% HS 12% Wendy WANG, BG Section David HIGGITT College of Global Change and Earth The University of Notthingham, System Science, Beijing Normal University Ningbo China Richard Gross PS 10% IG 8% Kun-Yeun HAN, HS Section Adam SWITZER OS 10% Kyungpook National University Earth Observatory of Singapore Atmospheric Sciences (AS) Biogeosciences (BG) James GOFF, IG Section Hydrological Sciences (HS) Interdisciplinary Geosciences (IG) University of New South Wales Jet Propulsion Laboratory Ocean Sciences (OS) Planetary Sciences (PS) Robin ROBERTSON, OS Section Solar & Terrestrial Sciences (ST) Solid Earth Sciences (SE) University of New South Wales at the Australian Defense Force Academy California Institute of Technology Fig 2. Representation by Country/Region Noriyuki NAMIKI, PS Section National Astronomical Observatory of Pasadena, CA 91109–8099, USA Japan Nanan BALAN, ST Section National Institute for Space Research (Instituto Nacional de Pesquisas Espaciais- Asia Oceania Geosciences Society INPE) th 13 Annual Meeting Hai Thanh TRAN, SE Section Hanoi University of Mining and Geology Partners & Supporters of AOGS July 31 to August 5, 2016 Beijing, China -

Meter-Scale Slopes of Candidate MER Landing Sites from Point Photoclinometry Ross A
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 108, NO. E12, 8085, doi:10.1029/2003JE002120, 2003 Meter-scale slopes of candidate MER landing sites from point photoclinometry Ross A. Beyer and Alfred S. McEwen Department of Planetary Sciences, University of Arizona, Tucson, Arizona, USA Randolph L. Kirk Astrogeology Team, U.S. Geological Survey, Flagstaff, Arizona, USA Received 13 May 2003; revised 16 July 2003; accepted 22 August 2003; published 4 December 2003. [1] Photoclinometry was used to analyze the small-scale roughness of areas that fall within the proposed Mars Exploration Rover (MER) 2003 landing ellipses. The landing ellipses presented in this study were those in Athabasca Valles, Elysium Planitia, Eos Chasma, Gusev Crater, Isidis Planitia, Melas Chasma, and Meridiani Planum. We were able to constrain surface slopes on length scales comparable to the image resolution (1.5 to 12 m/pixel). The MER 2003 mission has various engineering constraints that each candidate landing ellipse must satisfy. These constraints indicate that the statistical slope values at 5 m baselines are an important criterion. We used our technique to constrain maximum surface slopes across large swaths of each image, and built up slope statistics for the images in each landing ellipse. We are confident that all MER 2003 landing site ellipses in this study, with the exception of the Melas Chasma ellipse, are within the small-scale roughness constraints. Our results have provided input into the landing hazard assessment process. In addition to evaluating the safety of the landing sites, our mapping of small-scale roughnesses can also be used to better define and map morphologic units. -

Chandler and Annual Wobbles Based on Space-Geodetic Measurements
ISSN 1610-0956 Joachim Hopfner¨ Chandler and annual wobbles based on space-geodetic measurements Joachim Hopfner¨ Polar motions with a half-Chandler period and less in their temporal variability Scientific Technical Report STR02/13 Publication: Scientific Technical Report No.: STR02/13 Author: J. Hopfner¨ 1 Chandler and annual wobbles based on space-geodetic measurements Joachim Hopfner¨ GeoForschungsZentrum Potsdam (GFZ), Division Kinematics and Dynamics of the Earth, Telegrafenberg, 14473 Potsdam, Germany, e-mail: [email protected] Abstract. In this study, we examine the major components of polar motion, focusing on quantifying their temporal variability. In particular, by using the combined Earth orientation series SPACE99 computed by the Jet Propulsion Labo- ratory (JPL) from 1976 to 2000 at daily intervals, the Chandler and annual wobbles are separated by recursive band-pass ¦¥§£ filtering of the ¢¡¤£ and components. Then, for the trigonometric, exponential, and elliptic forms of representation, the parameters including their uncertainties are computed at epochs using quarterly sampling. The characteristics and temporal evolution of the wobbles are presented, as well as a summary of estimates of different parameters for four epochs. Key words: Polar motion, Chandler wobble, annual wobble, representation (trigonometric, exponential, elliptic), para- meter, variability, uncertainty 1 Introduction Variations in the Earth’s rotation provide fundamental information about the geophysical processes that occur in all components of the Earth. Therefore, the study of the Earth’s rotation is of great importance for understanding the dynamic interactions between the solid Earth, atmosphere, oceans and other geophysical fluids. In the rotating, terrestrial body-fixed reference frame, the variations of Earth rotation are measured by changes in length-of-day (LOD), and polar motion (PM).