Examining Differential Rotation on Stars Using the Matrix
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Detecting Differential Rotation and Starspot Evolution on the M Dwarf GJ 1243 with Kepler James R
Western Washington University Masthead Logo Western CEDAR Physics & Astronomy College of Science and Engineering 6-20-2015 Detecting Differential Rotation and Starspot Evolution on the M Dwarf GJ 1243 with Kepler James R. A. Davenport Western Washington University, [email protected] Leslie Hebb Suzanne L. Hawley Follow this and additional works at: https://cedar.wwu.edu/physicsastronomy_facpubs Part of the Stars, Interstellar Medium and the Galaxy Commons Recommended Citation Davenport, James R. A.; Hebb, Leslie; and Hawley, Suzanne L., "Detecting Differential Rotation and Starspot Evolution on the M Dwarf GJ 1243 with Kepler" (2015). Physics & Astronomy. 16. https://cedar.wwu.edu/physicsastronomy_facpubs/16 This Article is brought to you for free and open access by the College of Science and Engineering at Western CEDAR. It has been accepted for inclusion in Physics & Astronomy by an authorized administrator of Western CEDAR. For more information, please contact [email protected]. The Astrophysical Journal, 806:212 (11pp), 2015 June 20 doi:10.1088/0004-637X/806/2/212 © 2015. The American Astronomical Society. All rights reserved. DETECTING DIFFERENTIAL ROTATION AND STARSPOT EVOLUTION ON THE M DWARF GJ 1243 WITH KEPLER James R. A. Davenport1, Leslie Hebb2, and Suzanne L. Hawley1 1 Department of Astronomy, University of Washington, Box 351580, Seattle, WA 98195, USA; [email protected] 2 Department of Physics, Hobart and William Smith Colleges, Geneva, NY 14456, USA Received 2015 March 9; accepted 2015 May 6; published 2015 June 18 ABSTRACT We present an analysis of the starspots on the active M4 dwarf GJ 1243, using 4 years of time series photometry from Kepler. -
Dissertation Franz
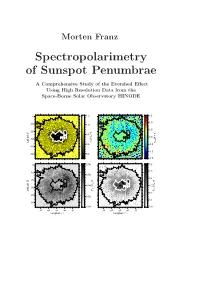
Morten Franz Spectropolarimetry of Sunspot Penumbrae A Comprehensive Study of the Evershed Effect Using High Resolution Data from the Space-Borne Solar Observatory HINODE 0 1.2 1.5 1.0 -10 1.0 0.5 ] ] -20 ″ -1 >] 0.8 qs I 0.0 [km s -30 [< c I dop Latitude [ v 0.6 -0.5 -40 -1.0 -50 0.4 -1.5 0 0.08 0.6 0.5 -10 0.06 0.4 ] -20 ″ >] >] qs qs I I 0.04 0.3 [< [< -30 lin cir P P Latitude [ 0.2 -40 0.02 0.1 -50 0.00 0.0 -70 -60 -50 -40 -30 -70 -60 -50 -40 -30 Longitude [″] Longitude [″] Cover Image: A sunspot at the center of the solar disk observed by HINODE on January 5th 2007. The panels show clockwise: Continuum Intensity, Doppler Velocity, and the inverse of Total Circular as well as Total Linear Polarization. Spectropolarimetry of Sunspot Penumbrae A Comprehensive Study of the Evershed Effect Using High Resolution Data from the Space-Borne Solar Observatory HINODE Inaugural-Dissertation zur Erlangung des Doktorgrades der Fakult¨at f¨ur Mathermatik und Physik der Albert-Ludwigs-Universit¨at Freiburg im Breisgau Morten Franz Kiepenheuer Institut f¨ur Sonnenphysik May 2011 Dekan: Prof. Dr. Kay K¨onigsmann Referent: Prof. Dr. Wolfgang Schmidt Korreferent: Prof. Dr. Svetlana Berdyugina Disputation: 21.06.2011 Publications and Conference Contributions Publication1 in Peer Reviewed Journals ➽ M. Franz J. Borrero, and R. Schlichenmaier, ”Reversal of NCP in penumbra at large heliocentric angles”, (2011), in preparation ➽ M. Franz and R. Schlichenmaier, ”Opposite Polarities in sunspot penumbrae”, (2011), in preparation A. -

General Disclaimer One Or More of The
General Disclaimer One or more of the Following Statements may affect this Document This document has been reproduced from the best copy furnished by the organizational source. It is being released in the interest of making available as much information as possible. This document may contain data, which exceeds the sheet parameters. It was furnished in this condition by the organizational source and is the best copy available. This document may contain tone-on-tone or color graphs, charts and/or pictures, which have been reproduced in black and white. This document is paginated as submitted by the original source. Portions of this document are not fully legible due to the historical nature of some of the material. However, it is the best reproduction available from the original submission. Produced by the NASA Center for Aerospace Information (CASI) THE EXTEM)ED CORONAL MAGNETIC FIELD _N 1 - 3 2 3 5_0 (ACCE5SION NUMBER) (THRU) O (PAGES) (CODE, (NASA CR OR TMX OR AD tf'UN DER) (CATE6;V) Series 11, Issue 74 October 16, 1970 UNIVERSITY Of CALIFORNIA, BERKELEY .'0 THE EXTENDED CORONAL MAGNETIC FIFID John M. Wilcox Technical Report ONR Contract N00014-69-A-0200-1016, Project NR 021 101 NASA Grant NGL 05-003-230 and NSF Grant GA-1319 Distribution of this document is unlimited. Reproduction in whole or in part is permitted for any purpose of the United States Government. To be published in the proceedings, NATO Advanced Study Institute on Physics of the Solar Corona, Athens, September 1970. r n sad x_ THE EXTENDED CORONAL MAGNETIC FIELD John M. -

Differential Rotation of Kepler-71 Via Transit Photometry Mapping of Faculae and Starspots
MNRAS 484, 618–630 (2019) doi:10.1093/mnras/sty3474 Advance Access publication 2019 January 16 Differential rotation of Kepler-71 via transit photometry mapping of faculae and starspots Downloaded from https://academic.oup.com/mnras/article-abstract/484/1/618/5289895 by University of Southern Queensland user on 14 November 2019 S. M. Zaleski ,1‹ A. Valio,2 S. C. Marsden1 andB.D.Carter1 1University of Southern Queensland, Centre for Astrophysics, Toowoomba 4350, Australia 2Center for Radio Astronomy and Astrophysics, Mackenzie Presbyterian University, Rua da Consolac¸ao,˜ 896 Sao˜ Paulo, Brazil Accepted 2018 December 19. Received 2018 December 18; in original form 2017 November 16 ABSTRACT Knowledge of dynamo evolution in solar-type stars is limited by the difficulty of using active region monitoring to measure stellar differential rotation, a key probe of stellar dynamo physics. This paper addresses the problem by presenting the first ever measurement of stellar differential rotation for a main-sequence solar-type star using starspots and faculae to provide complementary information. Our analysis uses modelling of light curves of multiple exoplanet transits for the young solar-type star Kepler-71, utilizing archival data from the Kepler mission. We estimate the physical characteristics of starspots and faculae on Kepler-71 from the characteristic amplitude variations they produce in the transit light curves and measure differential rotation from derived longitudes. Despite the higher contrast of faculae than those in the Sun, the bright features on Kepler-71 have similar properties such as increasing contrast towards the limb and larger sizes than sunspots. Adopting a solar-type differential rotation profile (faster rotation at the equator than the poles), the results from both starspot and facula analysis indicate a rotational shear less than about 0.005 rad d−1, or a relative differential rotation less than 2 per cent, and hence almost rigid rotation. -

The Milky Way Almost Every Star We Can See in the Night Sky Belongs to Our Galaxy, the Milky Way
The Milky Way Almost every star we can see in the night sky belongs to our galaxy, the Milky Way. The Galaxy acquired this unusual name from the Romans who referred to the hazy band that stretches across the sky as the via lactia, or “milky road”. This name has stuck across many languages, such as French (voie lactee) and spanish (via lactea). Note that we use a capital G for Galaxy if we are talking about the Milky Way The Structure of the Milky Way The Milky Way appears as a light fuzzy band across the night sky, but we also see individual stars scattered in all directions. This gives us a clue to the shape of the galaxy. The Milky Way is a typical spiral or disk galaxy. It consists of a flattened disk, a central bulge and a diffuse halo. The disk consists of spiral arms in which most of the stars are located. Our sun is located in one of the spiral arms approximately two-thirds from the centre of the galaxy (8kpc). There are also globular clusters distributed around the Galaxy. In addition to the stars, the spiral arms contain dust, so that certain directions that we looked are blocked due to high interstellar extinction. This dust means we can only see about 1kpc in the visible. Components in the Milky Way The disk: contains most of the stars (in open clusters and associations) and is formed into spiral arms. The stars in the disk are mostly young. Whilst the majority of these stars are a few solar masses, the hot, young O and B type stars contribute most of the light. -

Differential Rotation in Sun-Like Stars from Surface Variability and Asteroseismology
Differential rotation in Sun-like stars from surface variability and asteroseismology Dissertation zur Erlangung des mathematisch-naturwissenschaftlichen Doktorgrades “Doctor rerum naturalium” der Georg-August-Universität Göttingen im Promotionsprogramm PROPHYS der Georg-August University School of Science (GAUSS) vorgelegt von Martin Bo Nielsen aus Aarhus, Dänemark Göttingen, 2016 Betreuungsausschuss Prof. Dr. Laurent Gizon Institut für Astrophysik, Georg-August-Universität Göttingen Max-Planck-Institut für Sonnensystemforschung, Göttingen, Germany Dr. Hannah Schunker Max-Planck-Institut für Sonnensystemforschung, Göttingen, Germany Prof. Dr. Ansgar Reiners Institut für Astrophysik, Georg-August-Universität, Göttingen, Germany Mitglieder der Prüfungskommision Referent: Prof. Dr. Laurent Gizon Institut für Astrophysik, Georg-August-Universität Göttingen Max-Planck-Institut für Sonnensystemforschung, Göttingen Korreferent: Prof. Dr. Stefan Dreizler Institut für Astrophysik, Georg-August-Universität, Göttingen 2. Korreferent: Prof. Dr. William Chaplin School of Physics and Astronomy, University of Birmingham Weitere Mitglieder der Prüfungskommission: Prof. Dr. Jens Niemeyer Institut für Astrophysik, Georg-August-Universität, Göttingen PD. Dr. Olga Shishkina Max Planck Institute for Dynamics and Self-Organization Prof. Dr. Ansgar Reiners Institut für Astrophysik, Georg-August-Universität, Göttingen Prof. Dr. Andreas Tilgner Institut für Geophysik, Georg-August-Universität, Göttingen Tag der mündlichen Prüfung: 3 Contents 1 Introduction 11 1.1 Evolution of stellar rotation rates . 11 1.1.1 Rotation on the pre-main-sequence . 11 1.1.2 Main-sequence rotation . 13 1.1.2.1 Solar rotation . 15 1.1.3 Differential rotation in other stars . 17 1.1.3.1 Latitudinal differential rotation . 17 1.1.3.2 Radial differential rotation . 18 1.2 Measuring stellar rotation with Kepler ................... 19 1.2.1 Kepler photometry . -

Dynamo Processes Constrained by Solar and Stellar Observations Maria A
Long Term Datasets for the Understanding of Solar and Stellar Magnetic Cycles Proceedings IAU Symposium No. 340, 2018 c 2018 International Astronomical Union D. Banerjee, J. Jiang, K. Kusano, & S. Solanki, eds. DOI: 00.0000/X000000000000000X Dynamo Processes Constrained by Solar and Stellar Observations Maria A. Weber1,2 1Department of Astronomy and Astrophysics, University of Chicago 2Department of Astronomy, Adler Planetarium, Chicago, IL email: [email protected] Abstract. Our understanding of stellar dynamos has largely been driven by the phenomena we have observed of our own Sun. Yet, as we amass longer-term datasets for an increasing number of stars, it is clear that there is a wide variety of stellar behavior. Here we briefly review observed trends that place key constraints on the fundamental dynamo operation of solar-type stars to fully convective M dwarfs, including: starspot and sunspot patterns, various magnetism-rotation correlations, and mean field flows such as differential rotation and meridional circulation. We also comment on the current insight that simulations of dynamo action and flux emergence lend to our working knowledge of stellar dynamo theory. While the growing landscape of both observations and simulations of stellar magnetic activity work in tandem to decipher dynamo action, there are still many puzzles that we have yet to fully understand. Keywords. stars, Sun, activity, magnetic fields, interiors, observations, simulations 1. Introduction: Our Unique Dynamo Perspective Historically, our study of stellar dynamos has been shaped by observations of the Sun over a small portion of its existence. Magnetic braking facilitated through the solar wind has spun down the Sun from a likely chaotic youth to its current middle-aged state. -

Predicting the Sun's Polar Magnetic Fields with A
The Astrophysical Journal, 780:5 (8pp), 2014 January 1 doi:10.1088/0004-637X/780/1/5 C 2014. The American Astronomical Society. All rights reserved. Printed in the U.S.A. PREDICTING THE SUN’S POLAR MAGNETIC FIELDS WITH A SURFACE FLUX TRANSPORT MODEL Lisa Upton1,2 and David H. Hathaway3 1 Department of Physics and Astronomy, Vanderbilt University, VU Station B 1807, Nashville, TN 37235, USA; [email protected], [email protected] 2 Center for Space Physics and Aeronomy Research, The University of Alabama in Huntsville, Huntsville, AL 35899, USA 3 NASA Marshall Space Flight Center, Huntsville, AL 35812, USA; [email protected] Received 2013 September 25; accepted 2013 November 4; published 2013 December 6 ABSTRACT The Sun’s polar magnetic fields are directly related to solar cycle variability. The strength of the polar fields at the start (minimum) of a cycle determine the subsequent amplitude of that cycle. In addition, the polar field reversals at cycle maximum alter the propagation of galactic cosmic rays throughout the heliosphere in fundamental ways. We describe a surface magnetic flux transport model that advects the magnetic flux emerging in active regions (sunspots) using detailed observations of the near-surface flows that transport the magnetic elements. These flows include the axisymmetric differential rotation and meridional flow and the non-axisymmetric cellular convective flows (supergranules), all of which vary in time in the model as indicated by direct observations. We use this model with data assimilated from full-disk magnetograms to produce full surface maps of the Sun’s magnetic field at 15 minute intervals from 1996 May to 2013 July (all of sunspot cycle 23 and the rise to maximum of cycle 24). -

Graphical Evidence for the Solar Coronal Structure During the Maunder Minimum: Comparative Study of the Total Eclipse Drawings in 1706 and 1715
J. Space Weather Space Clim. 2021, 11,1 Ó H. Hayakawa et al., Published by EDP Sciences 2021 https://doi.org/10.1051/swsc/2020035 Available online at: www.swsc-journal.org Topical Issue - Space climate: The past and future of solar activity RESEARCH ARTICLE OPEN ACCESS Graphical evidence for the solar coronal structure during the Maunder minimum: comparative study of the total eclipse drawings in 1706 and 1715 Hisashi Hayakawa1,2,3,4,*, Mike Lockwood5,*, Matthew J. Owens5, Mitsuru Sôma6, Bruno P. Besser7, and Lidia van Driel – Gesztelyi8,9,10 1 Institute for Space-Earth Environmental Research, Nagoya University, 4648601 Nagoya, Japan 2 Institute for Advanced Researches, Nagoya University, 4648601 Nagoya, Japan 3 Science and Technology Facilities Council, RAL Space, Rutherford Appleton Laboratory, Harwell Campus, OX11 0QX Didcot, UK 4 Nishina Centre, Riken, 3510198 Wako, Japan 5 Department of Meteorology, University of Reading, RG6 6BB Reading, UK 6 National Astronomical Observatory of Japan, 1818588 Mitaka, Japan 7 Space Research Institute, Austrian Academy of Sciences, 8042 Graz, Austria 8 Mullard Space Science Laboratory, University College London, RH5 6NT Dorking, UK 9 LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris Diderot, Sorbonne Paris Cité, 92195 Meudon, France 10 Konkoly Observatory, Hungarian Academy of Sciences, 1121 Budapest, Hungary Received 18 October 2019 / Accepted 29 June 2020 Abstract – We discuss the significant implications of three eye-witness drawings of the total solar eclipse on 1706 May 12 in comparison with two on 1715 May 3, for our understanding of space climate change. These events took place just after what has been termed the “deep Maunder Minimum” but fall within the “extended Maunder Minimum” being in an interval when the sunspot numbers start to recover. -

Rotation and Stellar Evolution
EPJ Web of Conferences 43, 01005 (2013) DOI: 10.1051/epjconf/20134301005 C Owned by the authors, published by EDP Sciences, 2013 Rotation and stellar evolution P. Eggenbergera Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Sauverny, Suisse Abstract. The effects of rotation on the evolution and properties of low-mass stars are first discussed from the pre-main sequence to the red giant phase. We then briefly indicate how some observational constraints available for these stars can help us progress in our understanding of the dynamical processes at work in stellar interiors. 1. INTRODUCTION Rotation is an important physical process that can have a significant impact on stellar evolution (see e.g. [1]). Rotational effects have generally been included in stellar evolution codes in the context of shellular rotation, which assumes that a strongly anisotropic turbulence leads to an essentially constant angular velocity on the isobars [2]. Here, we first illustrate the impact of rotation on the properties of low-mass stars at different evolutionary phases by presenting models computed with the Geneva stellar evolution code that includes a detailed treatment of shellular rotation [3]. We then compare these models to some observational constraints available for low-mass stars, which are particularly useful to constrain the modelling of the dynamical processes operating in stellar interiors. 2. EFFECTS OF ROTATION 2.1 Pre-main sequence The effects of rotation during the pre-main sequence (PMS) evolution of solar-type stars are first briefly discussed (see [4] for a more detailed discussion). Figure 1 (left) illustrates the change in the HR diagram due to rotational effects during the PMS evolution of 1 M models with a solar chemical composition and a solar-calibrated parameter for the mixing-length. -

Galactic Rotation II
1 Galactic Rotation • See SG 2.3, BM ch 3 B&T ch 2.6,2.7 B&T fig 1.3 and ch 6 • Coordinate system: define velocity vector by π,θ,z π radial velocity wrt galactic center θ motion tangential to GC with positive values in direct of galactic rotation z motion perpendicular to the plane, positive values toward North If the galaxy is axisymmetric galactic pole and in steady state then each pt • origin is the galactic center (center or in the plane has a velocity mass/rotation) corresponding to a circular • Local standard of rest (BM pg 536) velocity around center of mass • velocity of a test particle moving in of MW the plane of the MW on a closed orbit that passes thru the present position of (π,θ,z)LSR=(0,θ0,0) with 2 the sun θ0 =θ0(R) Coordinate Systems The stellar velocity vectors are z:velocity component perpendicular to plane z θ: motion tangential to GC with positive velocity in the direction of rotation radial velocity wrt to GC b π: GC π With respect to galactic coordinates l +π= (l=180,b=0) +θ= (l=30,b=0) +z= (b=90) θ 3 Local standard of rest: assume MW is axisymmetric and in steady state If this each true each point in the pane has a 'model' velocity corresponding to the circular velocity around of the center of mass. An imaginery point moving with that velocity at the position of the sun is defined to be the LSR (π,θ,z)LSR=(0,θ0,0);whereθ0 = θ0(R0) 4 Description of Galactic Rotation (S&G 2.3) • For circular motion: relative angles and velocities observing a distant point • T is the tangent point V =R sinl(V/R-V /R ) r 0 0 0 Vr Because V/R drops with R (rotation curve is ~flat); for value 0<l<90 or 270<l<360 reaches a maximum at T max So the process is to find Vr for each l and deduce V(R) =Vr+R0sinl For R>R0 : rotation curve from HI or CO is degenerate ; use masers, young stars with known distances 5 Galactic Rotation- S+G sec 2.3, B&T sec 3.2 • Consider a star in the midplane of the Galactic disk with Galactic longitude, l, at a distance d, from the Sun. -

Solar Activity Reconstruction from Historical Observations of Sunspots
Solar Activity Reconstruction from Historical Observations of Sunspots Dissertation zur Erlangung des akademischen Grades doctor rerum naturalium (Dr. rer. nat.) in der Wissenschaftsdisziplin Astrophysik eingereicht an der Mathematisch-Naturwissenschaftlichen Fakultat¨ der Universitat¨ Potsdam Senthamizh Pavai Valliappan November 29, 2017 Leibniz-Institut fur¨ Astrophysik Potsdam An der Sternwarte 16 14482 Potsdam Universitat¨ Potsdam Institut fur¨ Physik und Astronomie Karl-Liebknecht-Strasse 24/25 14476 Potsdam-Golm Published online at the Institutional Repository of the University of Potsdam: URN urn:nbn:de:kobv:517-opus4-413600 http://nbn-resolving.de/urn:nbn:de:kobv:517-opus4-413600 Table of contents Abstract ............................................ 1 Zusammenfassung ...................................... 3 1 Introduction 5 1.1 The solar cycle ..................................... 6 1.2 Solar cycle properties .................................. 9 1.3 Indices of solar activity ................................. 11 1.3.1 Sunspot number ................................. 11 1.3.2 Sunspot area ................................... 12 1.3.3 Solar irradiance ................................. 13 1.4 Indirect solar indices .................................. 14 1.4.1 Geomagnetic activity ............................... 14 1.4.2 Aurorae ..................................... 15 1.4.3 Cosmogenic radionuclides ............................ 15 1.5 Reconstruction of solar activity ............................ 16 1.6 Solar dynamo .....................................