Applying Deep Neural Networks to Financial Time Series Forecasting
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Remember to Change Intro Slide Color As Needed
Simple AngularJS thanks to Best Practices Learn AngularJS the easy way Level 100-300 What’s this session about? 1. AngularJS can be easy when you understand basic concepts and best practices 2. But it can also be messy and difficult if you follow most online examples for just about anything I had to learn this the hard way I want to make it easier for you With know-how and sample code Quick Bad-Example Code Taken from AngularJS documentation. This example use the old $scope concept which you should avoid nowdays. Don’t worry if you don’t understand this – it’s meant to keep advanced developers in the room . 1. Demo 2. What is AngularJS 3. Deep Dive and Learn Goal: Get to know AngularJS based on a real App built with as many simple best practices as I could think of. Example AngularJS App Think of a DNN-Module, just simpler Live Demo Feedback given by anonymous users Feedback management for Admin users Download current edition http://2sxc.org/apps SoC Server and Client Server Concerns Client Concerns Storage of Data Form UI for new items Ability to deliver Data Instructs Server what to when needed do (Create, Read, …) Sorted Categories All/one Feedback Items List-UI for admin Ability to do other CRUD Change UIs when editing Create, Read, Update Delete Messages REST Dialogs Permissions on Content- refresh Types (allow create…) No code (zero c#) All code is on the client Look at the wire (live glimpse) Let’s watch these processes Recommended Tools Get Categories Chrome Debug Create Feedback-Item Firebug Get All Feedback -

Dual-Arm Peg-In-Hole Assembly Using DNN with Double Force/Torque Sensor
applied sciences Article Dual-Arm Peg-in-Hole Assembly Using DNN with Double Force/Torque Sensor David Ortega-Aranda 1,* , Julio Fernando Jimenez-Vielma 1 , Baidya Nath Saha 2 and Ismael Lopez-Juarez 3 1 Centro de Ingenieria y Desarrollo Industrial (CIDESI), Apodaca 66628, Mexico; [email protected] 2 Faculty of Science, Concordia University of Edmonton, Information Technology, Edmonton, AB T5B 4E4, Canada; [email protected] 3 Centre for Research and Advanced Studies (CINVESTAV), Ramos Arizpe 25900, Mexico; [email protected] * Correspondence: [email protected] Abstract: Assembly tasks executed by a robot have been studied broadly. Robot assembly applica- tions in industry are achievable by a well-structured environment, where the parts to be assembled are located in the working space by fixtures. Recent changes in manufacturing requirements, due to unpredictable demanded products, push the factories to seek new smart solutions that can au- tonomously recover from failure conditions. In this way, new dual arm robot systems have been studied to design and explore applications based on its dexterity. It promises the possibility to get rid of fixtures in assembly tasks, but using less fixtures increases the uncertainty on the location of the components in the working space. It also increases the possibility of collisions during the assembly sequence. Under these considerations, adding perception such as force/torque sensors have been done to produce useful data to perform control actions. Unfortunately, the interaction forces between mating parts produced non-linear behavior. Consequently, machine learning algorithms have been Citation: Ortega-Aranda, D.; Jimenez-Vielma, J.F.; Saha, B.N.; considered an alternative tool to avoid the non-linearity. -

Dotnetnuke Remote Code Execution Vulnerability Cve®1-2017-9822
DOTNETNUKE REMOTE CODE EXECUTION VULNERABILITY CVE®1-2017-9822 DISCUSSION DotNetNuke®2 (DNN), also known as DNN Evoq and DNN Evoq Engage, is a web-based Content Management System (CMS) developed on the Microsoft®3 .NET framework. DNN is a web application commonly deployed on local or cloud Microsoft Internet Information Service (IIS) servers. On July 7, 2017, security researchers revealed a vulnerability within DNN versions 5.2.0 through 9.1.0 that allows an attacker to forge valid DNN credentials and execute arbitrary commands on DNN web servers. Web-based applications, such as DNN, can be overlooked in routine patching since vulnerability scans may be unaware of their presence. Furthermore, administrators often postpone major version updates to web applications due to the frequent user impact and incompatibility with customized features. Web applications are a frequent target for attackers and vulnerabilities can be exploited days or even hours after their release. For this reason, configuring web applications to update automatically is imperative to secure web application servers. There are many web-based CMSs similar to DNN. Other common CMS’s are WordPress®4, Drupal®5 and Joomla®6. Organizations should be aware of CMS instances within their purview (i.e., blog, wiki, etc.) and ensure adequate processes are in place for timely updates. MITIGATION ACTIONS The most effective mitigation action is to update to the latest version of DNN, version 9.1.1, which is not vulnerable. A hotfix is available at dnnsoftware.com for older versions of DNN, but NSA recommends to only use the hotfix as a temporary measure while migrating to the latest version. -

Andrew Keats
Andrew Keats Genera Experienc Nationality British Aug 2019 - May 2020 Front-end Team Lead Date of Birth 12 November 1983 Toggle, Led delivery of a greenfield 187 Wardour Street, React-TypeScript SPA trading insight Soho app; complex data-driven UI using D3. Contac London Front-end Architect. In charge of a Telephone 07931998868 W1F 8ZB team of front-end developers; defined Email a [email protected] requirements, managed workloads. Defined best practices and set-up automated linting, unit tests and code Skill & Technologie quality processes. Responsible for CI Client & Front-end Development pipeline in GitLab, using Docker, Web Browser: TypeScript/JavaScript (ES5-2017, OO & NodeJS, and Kubernetes. Functional); Svelte, React, Aurelia, Backbone (SPA frameworks); Ramda, Lo-Dash, jQuery, (utility libraries); CSS, Oct 2018 – Aug 2019 Lead Front-end Developer SASS, PostCSS; HTML5 & Markdown; XML & XSLT. Equal Experts, Delivering a greenfield front-end service Desktop and Mobile: C#; .Net WinForms; Unity. 30 Brock St, for John Lewis, using GCP, Docker, Build tools: Parcel; Rollup; Webpack; Gulp; Grunt; Browserify. Kings Cross, NodeJS, isomorphic React with ES6 Test tools: RTL, Enzyme; Jest, Mocha, Karma, Jasmine; Cypress, London and modular SCSS. YAML driven CI. Selenium, ScalaTest.. NW1 3FG TDD using Jest; ATs using Kotlin and ChromeDriver. Back-end Development Server-side UIs: NodeJS with Polka/Express on GCP/Heroku, Apr 2017 – Sep 2017 Senior Front-end Developer SSR Svelte/React; Use of Scala with the Play framework & Clarksons Platou, Helping to deliver the front-end of a some Java; Experience with MS .Net (2-4), C#, use of DNN Commodity Quay, real-time, global shipping brokerage CMS and Episerver CMS; Experience with the Django St Katharine's & platform using TypeScript, Aurelia, AG framework; Some PHP (Wordpress & Laravel). -

State of the Software Supply Chain Report” - Kurzfassung (Executive Summary) Auf Deutsch
4. jährlicher “State of the Software Supply Chain Report” - Kurzfassung (Executive Summary) auf Deutsch. Einführung Vom Bank- bis zum Gesundheitswesen und von der Fertigungs- bis hin zur • Vermutete oder bekannte Open-Source-Sicherheitsverletzungen nahmen Unterhaltungsindustrie: Unternehmen, die in der Lage sind, innovative Soft- im Jahresvergleich um 55 % zu. ware-Anwendungen bereitzustellen, setzen etablierte Akteure unter Druck und • DevOps-Teams, die von Automatisierung profitieren, sind zu 90 % kon- gewinnen in jeder Branche an Bedeutung. form mit definierten Sicherheitsrichtlinien. Um am Ball bleiben und effektiv im Wettbewerb bestehen zu können, üben • Die Verwaltung von Software Supply Chains durch automatisierte CEOs und Aktionäre intensiven Druck auf IT-Führungskräfte aus, um das OSS-Governance reduziert vorhandene Schwachstellen um 50 %. Tempo der Software-Innovation zu beschleunigen. Als Reaktion darauf stellen Unternehmen Armeen von Software-Entwicklern ein, nutzen beispiellose • Gesetzliche Vorgaben in den Vereinigten Staaten und Europa deuten auf Mengen an Open-Source-Komponenten und statten Teams mit innovativen und eine zukünftige Software-Haftung hin. Cloud-basierten Tools aus, die den gesamten Lebenszyklus der Software-En- twicklung automatisieren und optimieren sollen. Im Gegensatz zum Bericht 2017 hebt der diesjährige Bericht neue Methoden hervor, mit denen Cyberkriminelle Software Supply Chains infiltrieren. Außerdem In dieser Welt ist Geschwindigkeit das A und O, Open Source ist allgegenwärtig bietet er erweiterte -

Request for Tender
REQUEST FOR TENDER RFT: 2021/018 File: AP 3/1/13 Date: 17 February, 2021 To: Interested suppliers Contact: Ainsof So’o, Systems Developer and Analyst Subject: Regional Technical Support Mechanism (RTSM) System Review and Upgrade 1. Background 1.1. The Secretariat of the Pacific Regional Environment Programme (SPREP) is an intergovernmental organisation charged with promoting cooperation among Pacific islands countries and territories to protect and improve their environment and ensure sustainable development. 1.2. SPREP approaches the environmental challenges faced by the Pacific guided by four simple Values. These values guide all aspects of our work: ▪ We value the Environment ▪ We value our People ▪ We value high quality and targeted Service Delivery ▪ We value Integrity 1.4. For more information, see www.sprep.org or https://rtsm.pacificclimatechange.net 2. Specifications: statement of requirement 2.1. SPREP is seeking the assistance of a short-term consultant to review and upgrade the RTSM. This work can be carried out remotely. 2.2. The Terms of Reference that detail the requirements and outputs of the consultancy are attached. 3. Conditions: information for applicants 3.1. To be considered for this work, interested suppliers must meet the following conditions: i. Submissions should include a workplan, schedule of activities and financial proposal. Please note all costs, including taxes, insurance and other costs are to be included in the financial proposal. Submitted proposals will be evaluated based evaluation criteria including best value for money. ii. Financial proposals should include the following: a. Fixed cost for the upgrade and migration through launch b. Hourly rate for requests outside of the initial migration and launch work (this is to cater for any additional requests that may arise) iii. -

Web Farm Configuration Guide
Web Farm Configuration Guide Version 4.1 Last Updated: March 2014 1 Notice Information in this document, including URL and other Internet Web site references, is subject to change without notice. The entire risk of the use or the results of the use of this document remains with the user. The example companies, organizations, products, domain names, e-mail addresses, logos, people, places, and events depicted herein are fictitious. No association with any real company, organization, product, domain name, email address, logo, person, places, or events is intended or should be inferred. Complying with all applicable copyright laws is the responsibility of the user. Without limiting the rights under copyright, no part of this document may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means (electronic, mechanical, photocopying, recording, or otherwise), or for any purpose, without the express written permission of DNN Corp. DNN Corp. may have patents, patent applications, trademarks, copyrights, or other intellectual property rights covering subject matter in this document. Except as expressly provided in any written license agreement from DNN Corporation, the furnishing of this document does not give you any license to these patents, trademarks, copyrights, or other intellectual property. Copyright © 2003-2014, DNN Corp. All Rights Reserved. DNN®, Evoq® and the DNN logo are either registered trademarks or trademarks of DNN Corp. in the United States and/or other countries. The names of actual companies and products mentioned herein may be the trademarks of their respective owners. 2 Abstract DNN Evoq Content is used for a broad range of websites; from single server installations to large enterprise class installs running in web farms. -

Dnn Free Video Gallery Module
Dnn free video gallery module Adding a video gallery doesn't have to be difficult. Keep your content and marketing materials up to date with easy-to-use video modules for DNN. This video walks you through installing and using the Lightbox Gallery module for DotNetNuke. This module. What is the best free video module that lets me upload and encode the video for The DotNetNuke Gallery module (v RC available at. Cross Video Gallery is an enterprise- class DNN module that enables multi-user Professional DNN modules, free DNN modules - DNN 7 Video & Audio & Youtube & Sideshow module - Cross Video Gallery - Demo Links. Coding Staff DotNetNuke Video Gallery is a powerful dnn media module that allows you to extend your Check free flv converting software by Coding Staff. Does anyone of you knows a free video gallery module? I would like to setup a page with videos in it? Can I just do it using media module or. It is ultra photo gallery framework built on top of DotNetNuke(DNN) platform. Ultra DNN Media Gallery Module with Image, Video & Slider Out of the box, you can manage your albums & photos; plus feel free to build your. Video player and video gallery module for the DotNetNuke Content Management System. Uses AJAX lists to provide a dynamic experience. Iphone and ipad. THE MOST Powerful DOTNETNUKE Free Touch Gallery Module. Responsive Touch Gallery Dnn / Dotnetnuke Module Video Tutorial. Videos Lorem ipsum dolor sit amet, consectetur adipiscing elit Lightbox gallery (supports images+video+audio) · Example 1 - Images with title and description. Easy Slider is a simple slider module and it's very easy to operate. -

Scalable and Distributed DNN Training on Modern HPC Systems
Scalable and Distributed DNN Training on Modern HPC Systems Talk at HPC-AI Competition (SCAsia ’19) by Dhabaleswar K. (DK) Panda The Ohio State University E-mail: [email protected] http://www.cse.ohio-state.edu/~panda Increasing Usage of HPC, Big Data and Deep Learning Big Data HPC (Hadoop, Spark, (MPI, RDMA, HBase, Lustre, etc.) Memcached, etc.) Convergence of HPC, Big Deep Learning Data, and Deep Learning! (Caffe, TensorFlow, BigDL, etc.) Increasing Need to Run these applications on the Cloud!! Network Based Computing Laboratory HPC-AI (SCAsia ‘19) 2 Drivers of Modern HPC Cluster Architectures High Performance Interconnects - Accelerators / Coprocessors InfiniBand high compute density, high Multi-core Processors <1usec latency, 200Gbps Bandwidth> performance/watt SSD, NVMe-SSD, NVRAM >1 TFlop DP on a chip • Multi-core/many-core technologies • Remote Direct Memory Access (RDMA)-enabled networking (InfiniBand and RoCE) • Solid State Drives (SSDs), Non-Volatile Random-Access Memory (NVRAM), NVMe-SSD • Accelerators (NVIDIA GPGPUs and Intel Xeon Phi) • Available on HPC Clouds, e.g., Amazon EC2, NSF Chameleon, Microsoft Azure, etc. Summit Sierra Sunway TaihuLight K - Computer Network Based Computing Laboratory HPC-AI (SCAsia ‘19) 3 Scale-up and Scale-out • Scale-up: Intra-node Communication NCCL2 – Many improvements like: NCCL1 Desired • NVIDIA cuDNN, cuBLAS, NCCL, etc. • CUDA 9 Co-operative Groups cuDNN MPI • Scale-out: Inter-node Communication MKL-DNN – DL Frameworks – most are optimized for single-node only up Performance up – Distributed -

How to Do a Performance Audit of Your .NET Website
WEB CMS MIGRATION HANDBOOK Of all the tasks that make up a content management system (CMS) implementation, there’s one that’s invariably underestimated, under budgeted, unscheduled, or even outright forgotten: content migration. If you’re implementing a new CMS, then you often have content—text and files—in your existing CMS system which has to be moved before you can launch. When someone builds a new house, they never forget that they have to move all their furniture from their existing house. However, when an organization builds a new website, it’s somehow all too easy to think that the content magically makes its way to the new CMS. Sadly, it’s never that simple. When planning for a migration, the content manager has to answer three fundamental questions: The Editorial Question: what content needs to migrate? 3 The Functional Question: how will content 5 in the existing system be managed in the new system? The Technical Question: how will the actual bytes 8 of content be exported from the existing system and imported to the new system? Answering these three questions are the core of any successful migration. 2 Web CMS Migration Handbook THE EDITORIAL QUESTION: WHAT CONTENT TO MIGRATE? Fundamental to any migration project is to determine what content is migrating. Remember, the easiest content to migrate is content you discard. That may seem flippant, but there’s almost invariably a chunk of content in any CMS that’s no longer necessary. This is content that’s redundant, outdated, or trivial. Any content migration should start with a comprehensive audit of what content exists on the current site. -
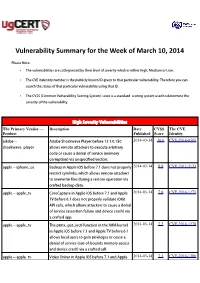
Vulnerability Summary for the Week of March 10, 2014
Vulnerability Summary for the Week of March 10, 2014 Please Note: • The vulnerabilities are cattegorized by their level of severity which is either High, Medium or Low. • The !" indentity number is the #ublicly $nown %& given to that #articular vulnerability. Therefore you can search the status of that #articular vulnerability using that %&. • The !'S (Common !ulnerability 'coring System) score is a standard scoring system used to determine the severity of the vulnerability. High Severity Vulnerabilities The Primary Vendor --- Description Date CVSS The CVE Product Published Score Identity adobe ** ,dobe 'hoc$wave Player before -..-.0.10/ 2014-03-14 10.0 CVE-2014-0505 shoc$wave+#layer allows remote attac$ers to e1ecute arbitrary code or cause a denial of service (memory corru#tion) via uns#ecified vectors. a##le ** i#hone+os 2ac$u# in ,##le i3' before 4.1 does not #roperly 2014-03-14 8.8 CVE-2013-5133 restrict symlin$s, which allows remote attac$ers to overwrite files during a restore operation via crafted bac$u# data. a##le ** a##le+tv ore a#ture in ,##le i3' before 4.- and ,##le 2014-03-14 7.8 CVE-2014-1271 T! before 5.1 does not #roperly validate %36it ,P% calls, which allows attac$ers to cause a denial of service (assertion failure and device crash) via a crafted a##. a##le ** a##le+tv The #tm1+get+ioctl function in the ,7M $ernel 2014-03-14 7.2 CVE-2014-1278 in ,##le i3' before 4.- and ,##le T! before 5.1 allows local users to gain #rivileges or cause a denial of service (out*of*bounds memory access and device crash) via a crafted call. -

Clarity Ventures Proposal
TABLE OF CONTENTS Prepared for Williamson County ITS PROPOSAL LINE ITEMS DNN Website Development / Support Services Clarity DNN Development Experience TASKS AND TIME ESTIMATES SERVICE ITEM ESTIMATE DESCRIPTION Hours Cost Website Development / Support Services Design Support Services DNN Website 80 $14,000 Clarity will provide Williamson County DNN content management system related support Maintenance & for County’s website(s), including but not limited to troubleshooting, configuration, Support Services updating, optimization, development, administration and training. Examples of services could include the following: • Troubleshoot website issues • Optimize DNN website to ensure stable environment • Setup development environment for offline changes • Update software and modules as needed • Develop/implement web pages as requested • Configure/administer DNN website(s) as required SUMMARY Total 80 $14,000 *Pricing assumes post-pay rates NOTES: Clarity has two payment rates, depending on client’s preferred payment method of either our Pre-payment or Post-payment models. Our Pre-pay model, which is a purchase of hours prior to work, offers a preferred client discount on our rates of $125/hour for front-end, design services, etc. and $150/hour for back-end, custom development, database, integration services, etc. The Post-pay model offers our standard billing rates of $150/hour, $175/hour respectively. The post-pay model is when payment is made after work has been done and is invoiced by Clarity every 30 days for work completed on NET 30 terms.