DOCSLIB.ORG

Commodity Option Pricing Is a Must-Read for Option Traders, Risk Managers and Quantita- Tive Analysts

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Commodity Option Pricing Is a Must-Read for Option Traders, Risk Managers and Quantita- Tive Analysts “It has been very hard to find a comprehensive option pricing book cover- ing all exchange-traded commodities, until Iain Clark’s book. Commodity Option Pricing is a must-read for option traders, risk managers and quantita- tive analysts. The author combines academic rigor with real-world examples. Practitioners can find an extremely useful toolkit in option pricing andan excellent introduction to various commodities.” Joseph Y. Chen, Chief, Market Analytics, Nexen “Being himself a practitioner with a wealth of experience, Iain knows what is relevant to the daily work of commodities trading desks. He uses his remarkable pedagogical skills to develop the reader’s intuition for the mod- els and products before delving into the practicalities of the commodities markets. Many of the details covered in this book cannot be found elsewhere in the literature. I am pleased to recommend this book to quants and traders, who will soon find themselves relying on it in their daily work.” Paul Bilokon, Director, Deutsche Bank “Option pricing analytics for trading commodity derivatives can be quite different from those of equity and fixed income derivatives. This book fills a gap in current literature by presenting a comprehensive treatise on the risk characteristics associated with pricing and hedging commodity derivatives. The author strikes a fine balance between option pricing theory and financial practice in the markets. The materials are succinctly written, with clear and insightful descriptions of the features of various commodity markets and state-of-the-art pricing models. This book is destined to be a valuable prac- tical guide for practitioners and a useful academic reference for researchers in trading and understanding commodities derivatives.” Yue Kuen Kwok, Professor, Department of Mathematics, Hong Kong University of Science and Technology Commodity Option Pricing For other titles in the Wiley Finance series please see www.wiley.com/finance Commodity Option Pricing A Practitioner’s Guide Iain J. Clark This edition first published 2014 © 2014 Iain J. Clark Registered office John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom For details of our global editorial offices, for customer services and for information about howto apply for permission to reuse the copyright material in this book please see our website at www.wiley.com. The right of the author to be identified as the author of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher. Wiley publishes in a variety of print and electronic formats and by print-on-demand. Some material included with standard print versions of this book may not be included in e-books or in print-on-demand. If this book refers to media such as a CD or DVD that is not included in the version you purchased, you may download this material at http://booksupport.wiley.com. For more information about Wiley products, visit www.wiley.com. Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book. Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with the respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. It is sold on the understanding that the publisher is not engaged in rendering professional services and neither the publisher nor the author shall be liable for damages arising herefrom. If professional advice or other expert assistance is required, the services of a competent professional should be sought. Library of Congress Cataloging-in-Publication Data Clark, Iain J. Commodity option pricing : a practitioners guide / Iain J. Clark. pages cm Includes bibliographical references and index. ISBN 978-1-119-94451-5 (cloth) 1. Commodity options. 2. Options (Finance)–Prices. I. Clark, Iain J. II. Title. HG6046.C5736 2014 332.63′28–dc23 2013051276 A catalogue record for this book is available from the British Library. ISBN 978-1-119-94451-5 (hbk) ISBN 978-1-444-36240-4 (ebk) ISBN 978-1-444-36241-1 (ebk) ISBN 978-1-118-87178-2 (ebk) Cover images reproduced by permission of Shutterstock.com Set in 11/13pt Times by Aptara Inc., New Delhi, India Printed in Great Britain by TJ International Ltd, Padstow, Cornwall, UK For Elizabeth Clark (born July 2013). Who made the completion of this book a challenge – in the nicest possible way. Contents Acknowledgements xv Notation xvii List of Figures xix List of Tables xxiii 1 Introduction 1 1.1 Trade, Commerce and Commodities 3 1.2 Adapting to Commodities as an Asset Class 8 1.2.1 Classification of Commodities into Sub-categories 9 1.3 Challenges in Commodity Models 12 1.3.1 Futures 12 1.3.2 Correlation 12 1.3.3 Seasonality 15 1.3.4 American and Asian Features 15 2 Commodity Mathematics and Products 17 2.1 Spot, Forwards and Futures 17 2.1.1 Spot 18 2.1.2 Forwards 19 2.1.3 Futures 20 2.2 The Black–Scholes and Black-76 Models 24 2.2.1 The Black–Scholes Model 24 x Contents 2.2.2 The Black–Scholes Model Without Convenience Yield 25 2.2.3 The Black–Scholes Model With Convenience Yield 26 2.2.4 The Black-76 Model 28 2.2.5 Risk-Neutral Valuation 35 2.2.6 Forwards 36 2.2.7 The Black–Scholes Term Structure Model 38 2.3 Forward and Futures Contracts 39 2.3.1 Forwards 39 2.3.2 Futures 39 2.3.3 Case Study 40 2.4 Commodity Swaps 42 2.5 European Options 44 2.5.1 European Options on Spot 45 2.5.2 European Options on Futures 49 2.5.3 Settlement Adjustments 49 2.6 American Options 50 2.6.1 Barone-Adesi and Whaley (1987) 50 2.6.2 Lattice Methods 53 2.7 Asian Options 54 2.7.1 Geometric Asian Options – Continuous Averaging 54 2.7.2 Arithmetic Asian Options – Continuous Averaging 61 2.7.3 Geometric Average Options – Discrete Fixings – Kemna and Vorst (1990) 62 2.7.4 Arithmetic Average Options – Discrete Fixings – Turnbull and Wakeman (1991) 66 2.8 Commodity Swaptions 70 2.9 Spread Options 73 2.9.1 Margrabe Exchange Options 74 2.9.2 The Kirk Approximation 75 2.9.3 Calendar Spread Options 77 2.9.4 Asian Spread Options 78 2.10 More Advanced Models 78 2.10.1 Mean Reverting Models 79 2.10.2 Multi-Factor Models 88 2.10.3 Convenience Yield Models 94 Contents xi 3 Precious Metals 99 3.1 Gold Forward and Gold Lease Rates 101 3.2 Volatility Surfaces for Precious Metals 103 3.2.1 Pips Spot Delta 104 3.2.2 Pips Forward Delta 104 3.2.3 Notation 105 3.2.4 Market Volatility Surfaces 105 3.2.5 At-the-Money 105 3.2.6 Strangles and Risk Reversals 107 3.2.7 Temporal Interpolation 111 3.3 Survey of the Precious Metals 111 3.3.1 Gold 112 3.3.2 Silver 117 3.3.3 Platinum 119 3.3.4 Palladium 121 3.3.5 Rhodium 124 4 Base Metals 127 4.1 Futures, Options and TAPO Contracts 130 4.1.1 Futures 130 4.1.2 Options 134 4.1.3 Traded Average Price Options 137 4.2 Commonly Traded Base Metals 139 4.2.1 Copper 140 4.2.2 Aluminium 142 4.2.3 Zinc 143 4.2.4 Nickel 145 4.2.5 Lead 146 4.2.6 Tin 148 5 Energy I – Crude Oil, Natural Gas and Coal 151 5.1 Crude Oil 154 5.1.1 WTI 158 5.1.2 Brent 163 5.1.3 Calibration of WTI Volatility Term Structure 171 5.1.4 Calibration of WTI Volatility Skew 174 5.1.5 Brent and Other Crude Markets 177 5.1.6 A Note on Correlation 180 xii Contents 5.2 Natural Gas 180 5.2.1 Deseasonalising Forward Curves 186 5.3 Coal 188 6 Energy II – Refined Products 195 6.1 The Refinery Basket 195 6.2 Gasoline 197 6.3 Heating Oil/Gas Oil 200 6.4 Petroleum Gases and Residual Fuel Oil 203 6.5 Seasonality and Volatility 205 6.6 Crack Spread Options 207 7 Power 213 7.1 Electricity Generation 214 7.2 Nonstorability and Decorrelation 217 7.2.1 Spot Markets 218 7.2.2 Futures and Forward Markets 219 7.2.3 Options Markets 220 7.3 Modelling Spikes in Electricity Markets 220 7.3.1 Reduced Form Models 223 7.3.2 Structural Models 227 7.4 Swing Options 231 7.5 Spark Spread Options 232 8 Agricultural Derivatives 233 8.1 Grains 234 8.1.1 Wheat 236 8.1.2 Corn 239 8.1.3 Rice 240 8.1.4 Oats 241 8.1.5 Barley 241 8.2 Oilseeds 242 8.2.1 Soybeans 242 8.2.2 Canola 244 8.3 Softs 244 8.3.1 Coffee 245 8.3.2 Cotton 247 8.3.3 Cocoa 248 8.3.4 Sugar 249 Contents xiii 8.3.5 Orange Juice 250 8.3.6 Lumber 252 8.4 Pulp and Paper 252 8.5 Livestock 253 8.5.1 Feeder Cattle 253 8.5.2 Live Cattle 254 8.5.3 Lean Hogs 255 8.5.4 Pork Bellies 255 8.5.5 Milk and Dairy 256 9 Alternative Commodities 257 9.1 Carbon Emissions Trading 257 9.2 Weather Derivatives 261 9.2.1 Temperature Derivatives 261 9.2.2 Windspeed Derivatives 263 9.2.3 Precipitation Derivatives 263 9.3 Bandwidth and Telecommunication Trading 264 9.4 Plastics 265 9.5 Freight Derivatives 266 9.5.1 Shipping 266 9.5.2 Pricing and the Baltic Freight Market 268 9.5.3 Forward Freight Agreements and Options 269 Conversion Factors 273 Futures Contract Symbols 275 Glossary 279 References 295 Further Reading 303 Index 307 Acknowledgements Firstly, I would like to thank my wife yet again for her incredible patience and fortitude during the completion of this work, which somehow coin- cided with the happy arrival of our daughter Elizabeth; my efforts to finish the book in nine months were not nearly so successful.
Load more

Recommended publications
  • Here We Go Again
    2015, 2016 MDDC News Organization of the Year! Celebrating 161 years of service! Vol. 163, No. 3 • 50¢ SINCE 1855 July 13 - July 19, 2017 TODAY’S GAS Here we go again . PRICE Rockville political differences rise to the surface in routine commission appointment $2.28 per gallon Last Week pointee to the City’s Historic District the three members of “Team him from serving on the HDC. $2.26 per gallon By Neal Earley @neal_earley Commission turned into a heated de- Rockville,” a Rockville political- The HDC is responsible for re- bate highlighting the City’s main po- block made up of Council members viewing applications for modification A month ago ROCKVILLE – In most jurisdic- litical division. Julie Palakovich Carr, Mark Pierzcha- to the exteriors of historic buildings, $2.36 per gallon tions, board and commission appoint- Mayor Bridget Donnell Newton la and Virginia Onley who ran on the as well as recommending boundaries A year ago ments are usually toward the bottom called the City Council’s rejection of same platform with mayoral candi- for the City’s historic districts. If ap- $2.28 per gallon of the list in terms of public interest her pick for Historic District Commis- date Sima Osdoby and city council proved Giammo, would have re- and controversy -- but not in sion – former three-term Rockville candidate Clark Reed. placed Matthew Goguen, whose term AVERAGE PRICE PER GALLON OF Rockville. UNLEADED REGULAR GAS IN Mayor Larry Giammo – political. While Onley and Palakovich expired in May. MARYLAND/D.C. METRO AREA For many municipalities, may- “I find it absolutely disappoint- Carr said they opposed Giammo’s ap- Giammo previously endorsed ACCORDING TO AAA oral appointments are a formality of- ing that politics has entered into the pointment based on his lack of qualifi- Newton in her campaign against ten given rubberstamped approval by boards and commission nomination cations, Giammo said it was his polit- INSIDE the city council, but in Rockville what process once again,” Newton said.
    [Show full text]
  • Derivative Markets Swaps.Pdf
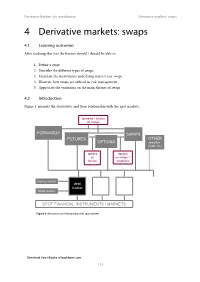
    Derivative Markets: An Introduction Derivative markets: swaps 4 Derivative markets: swaps 4.1 Learning outcomes After studying this text the learner should / should be able to: 1. Define a swap. 2. Describe the different types of swaps. 3. Elucidate the motivations underlying interest rate swaps. 4. Illustrate how swaps are utilised in risk management. 5. Appreciate the variations on the main themes of swaps. 4.2 Introduction Figure 1 presentsFigure the derivatives 1: derivatives and their relationshipand relationship with the spotwith markets. spot markets forwards / futures on swaps FORWARDS SWAPS FUTURES OTHER OPTIONS (weather, credit, etc) options options on on swaps = futures swaptions money market debt equity forex commodity market market market markets bond market SPOT FINANCIAL INSTRUMENTS / MARKETS Figure 1: derivatives and relationship with spot markets Download free eBooks at bookboon.com 116 Derivative Markets: An Introduction Derivative markets: swaps Swaps emerged internationally in the early eighties, and the market has grown significantly. An attempt was made in the early eighties in some smaller to kick-start the interest rate swap market, but few money market benchmarks were available at that stage to underpin this new market. It was only in the middle nineties that the swap market emerged in some of these smaller countries, and this was made possible by the creation and development of acceptable benchmark money market rates. The latter are critical for the development of the derivative markets. We cover swaps before options because of the existence of options on swaps. This illustration shows that we find swaps in all the spot financial markets. A swap may be defined as an agreement between counterparties (usually two but there can be more 360° parties involved in some swaps) to exchange specific periodic cash flows in the future based on specified prices / interest rates.
    [Show full text]
  • Variance Reduction with Control Variate for Pricing Asian Options in a Geometric Lévy Model
    IAENG International Journal of Applied Mathematics, 41:4, IJAM_41_4_05 ______________________________________________________________________________________ Variance Reduction with Control Variate for Pricing Asian Options in a Geometric Levy´ Model Wissem Boughamoura and Faouzi Trabelsi Abstract—This paper is concerned with Monte Carlo simu- use of the path integral formulation. [19] studied a cer- lation of generalized Asian option prices where the underlying tain one-dimensional, degenerate parabolic partial differential asset is modeled by a geometric (finite-activity) Levy´ process. equation with a boundary condition which arises in pricing A control variate technique is proposed to improve standard Monte Carlo method. Some convergence results for plain Monte of Asian options. [25] considered the approximation of Carlo simulation of generalized Asian options are proven, and a the optimal stopping problem associated with ultradiffusion detailed numerical study is provided showing the performance processes in valuating Asian options. The value function is of the variance reduction compared to straightforward Monte characterized as the solution of an ultraparabolic variational Carlo method. inequality. Index Terms—Levy´ process, Asian options, Minimal-entropy martingale measure, Monte Carlo method, Variance Reduction, For discontinuous markets, [8] generalized Laplace trans- Control variate. form for continuously sampled Asian option where under- lying asset is driven by a Levy´ Process, [18] presented a binomial tree method for Asian options under a particular I. INTRODUCTION jump-diffusion model. But such Market may be incomplete. He pricing of Asian options is a delicate and interesting Therefore, it will be a big class of equivalent martingale T topic in quantitative finance, and has been a topic of measures (EMMs). For the choice of suitable one, many attention for many years now.
    [Show full text]
  • Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces
    DEGREE PROJECT IN MATHEMATICS, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2020 Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ENGINEERING SCIENCES Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON Degree Projects in Mathematical Statistics (30 ECTS credits) Master's Programme in Applied and Computational Mathematics (120 credits) KTH Royal Institute of Technology year 2020 Supervisor at Nasdaq Technology AB: Sebastian Lindberg Supervisor at KTH: Fredrik Viklund Examiner at KTH: Fredrik Viklund TRITA-SCI-GRU 2020:081 MAT-E 2020:044 Royal Institute of Technology School of Engineering Sciences KTH SCI SE-100 44 Stockholm, Sweden URL: www.kth.se/sci Abstract The implied volatility surface plays an important role for Front office and Risk Manage- ment functions at Nasdaq and other financial institutions which require mark-to-market of derivative books intraday in order to properly value their instruments and measure risk in trading activities. Based on the aforementioned business needs, being able to calibrate an end of day implied volatility surface based on new market information is a sought after trait. In this thesis a statistical learning approach is used to calibrate the implied volatility surface intraday. This is done by using OMXS30-2019 implied volatil- ity surface data in combination with market information from close to at the money options and feeding it into 3 Machine Learning models. The models, including Feed For- ward Neural Network, Recurrent Neural Network and Gaussian Process, were compared based on optimal input and data preprocessing steps.
    [Show full text]
  • Futures and Options Workbook
    EEXAMININGXAMINING FUTURES AND OPTIONS TABLE OF 130 Grain Exchange Building 400 South 4th Street Minneapolis, MN 55415 www.mgex.com [email protected] 800.827.4746 612.321.7101 Fax: 612.339.1155 Acknowledgements We express our appreciation to those who generously gave their time and effort in reviewing this publication. MGEX members and member firm personnel DePaul University Professor Jin Choi Southern Illinois University Associate Professor Dwight R. Sanders National Futures Association (Glossary of Terms) INTRODUCTION: THE POWER OF CHOICE 2 SECTION I: HISTORY History of MGEX 3 SECTION II: THE FUTURES MARKET Futures Contracts 4 The Participants 4 Exchange Services 5 TEST Sections I & II 6 Answers Sections I & II 7 SECTION III: HEDGING AND THE BASIS The Basis 8 Short Hedge Example 9 Long Hedge Example 9 TEST Section III 10 Answers Section III 12 SECTION IV: THE POWER OF OPTIONS Definitions 13 Options and Futures Comparison Diagram 14 Option Prices 15 Intrinsic Value 15 Time Value 15 Time Value Cap Diagram 15 Options Classifications 16 Options Exercise 16 F CONTENTS Deltas 16 Examples 16 TEST Section IV 18 Answers Section IV 20 SECTION V: OPTIONS STRATEGIES Option Use and Price 21 Hedging with Options 22 TEST Section V 23 Answers Section V 24 CONCLUSION 25 GLOSSARY 26 THE POWER OF CHOICE How do commercial buyers and sellers of volatile commodities protect themselves from the ever-changing and unpredictable nature of today’s business climate? They use a practice called hedging. This time-tested practice has become a stan- dard in many industries. Hedging can be defined as taking offsetting positions in related markets.
    [Show full text]
  • How Options Implied Probabilities Are Calculated
    No content left No content right of this line of this line How Options Implied Probabilities Are Calculated The implied probability distribution is an approximate risk-neutral distribution derived from traded option prices using an interpolated volatility surface. In a risk-neutral world (i.e., where we are not more adverse to losing money than eager to gain it), the fair price for exposure to a given event is the payoff if that event occurs, times the probability of it occurring. Worked in reverse, the probability of an outcome is the cost of exposure Place content to the outcome divided by its payoff. Place content below this line below this line In the options market, we can buy exposure to a specific range of stock price outcomes with a strategy know as a butterfly spread (long 1 low strike call, short 2 higher strikes calls, and long 1 call at an even higher strike). The probability of the stock ending in that range is then the cost of the butterfly, divided by the payout if the stock is in the range. Building a Butterfly: Max payoff = …add 2 …then Buy $5 at $55 Buy 1 50 short 55 call 1 60 call calls Min payoff = $0 outside of $50 - $60 50 55 60 To find a smooth distribution, we price a series of theoretical call options expiring on a single date at various strikes using an implied volatility surface interpolated from traded option prices, and with these calls price a series of very tight overlapping butterfly spreads. Dividing the costs of these trades by their payoffs, and adjusting for the time value of money, yields the future probability distribution of the stock as priced by the options market.
    [Show full text]
  • An Asset Manager's Guide to Swap Trading in the New Regulatory World
    CLIENT MEMORANDUM An Asset Manager’s Guide to Swap Trading in the New Regulatory World March 11, 2013 As a result of the Dodd-Frank Act, the over-the-counter derivatives markets Contents have become subject to significant new regulatory oversight. As the Swaps, Security-Based markets respond to these new regulations, the menu of derivatives Swaps, Mixed Swaps and Excluded Instruments ................. 2 instruments available to asset managers, and the costs associated with those instruments, will change significantly. As the first new swap rules Key Market Participants .............. 4 have come into effect in the past several months, market participants have Cross-Border Application of started to identify risks and costs, as well as new opportunities, arising from the U.S. Swap Regulatory this new regulatory landscape. Regime ......................................... 7 Swap Reporting ........................... 8 This memorandum is designed to provide asset managers with background information on key aspects of the swap regulatory regime that may impact Swap Clearing ............................ 12 their derivatives trading activities. The memorandum focuses largely on the Swap Trading ............................. 15 regulations of the CFTC that apply to swaps, rather than on the rules of the Uncleared Swap Margin ............ 16 SEC that will govern security-based swaps, as virtually none of the SEC’s security-based swap rules have been adopted. Swap Dealer Business Conduct and Swap This memorandum first provides background information on the types of Documentation Rules ................ 19 derivatives that are subject to the CFTC’s swap regulatory regime, on new Position Limits and Large classifications of market participants created by the regime, and on the Trader Reporting ....................... 22 current approach to the cross-border application of swap requirements.
    [Show full text]
  • Risk Management Strategies for Cattlemen
    RISK MANAGEMENT STRATEGIES FOR CATTLEMEN Kurtis Ward – President/CEO www.kisokc.com As a former agricultural loan officer, I witnessed first-hand the effects that the Dairy Herd Buyout Program had on the Cattle Market of 1986. During this time, I became intrigued by cattlemen who used some form of risk management (Futures, Options, Forward Contracting, etc.) as compared to those who did nothing but speculate on the cash market. It didn’t take long to observe which group made better financial and marketing decisions (perhaps that “hedging stuff” that my college professors were teaching was really important after all). This market event caused my loan officer career to be transformed into a new profession as a commodity futures broker who specialized in risk management strategies for cattlemen. However, my naïve belief back then was that everyone else was having this “illumination” about cattle hedging at the same time. In the 1980’s, it was said that less than 5% of cattlemen were involved in risk management. Fifteen years later, things haven’t changed much which is quite surprising when you look at the total dollars now at risk in any cattle operation. After what we’ve seen during the cattle market of the past two years, I truly believe that cattlemen cannot afford to be just cattlemen any longer. Rather, they must first be “businessmen” who incidentally invest their, time, money and livelihood in a cattle operation. Therefore, the purpose of this article is to quickly review the basics of several risk management strategies in a way that is very simplistic so that the foundational hedging precepts can be easily understood.
    [Show full text]
  • Unified Pricing of Asian Options
    Unified Pricing of Asian Options Jan Veˇceˇr∗ ([email protected]) Assistant Professor of Mathematical Finance, Department of Statistics, Columbia University. Visiting Associate Professor, Institute of Economic Research, Kyoto University, Japan. First version: August 31, 2000 This version: April 25, 2002 Abstract. A simple and numerically stable 2-term partial differential equation characterizing the price of any type of arithmetically averaged Asian option is given. The approach includes both continuously and discretely sampled options and it is easily extended to handle continuous or dis- crete dividend yields. In contrast to present methods, this approach does not require to implement jump conditions for sampling or dividend days. Asian options are securities with payoff which depends on the average of the underlying stock price over certain time interval. Since no general analytical solution for the price of the Asian option is known, a variety of techniques have been developed to analyze arithmetic average Asian options. There is enormous literature devoted to study of this option. A number of approxima- tions that produce closed form expressions have appeared, most recently in Thompson (1999), who provides tight analytical bounds for the Asian option price. Geman and Yor (1993) computed the Laplace transform of the price of continuously sampled Asian option, but numerical inversion remains problematic for low volatility and/or short maturity cases as shown by Fu, Madan and Wang (1998). Very recently, Linetsky (2002) has derived new integral formula for the price of con- tinuously sampled Asian option, which is again slowly convergent for low volatility cases. Monte Carlo simulation works well, but it can be computationally expensive without the enhancement of variance reduction techniques and one must account for the inherent discretization bias result- ing from the approximation of continuous time processes through discrete sampling as shown by Broadie, Glasserman and Kou (1999).
    [Show full text]
  • Evaluating the Performance of the WTI
    An Evaluation of the Performance of Oil Price Benchmarks During the Financial Crisis Craig Pirrong Professor of Finance Energy Markets Director, Global Energy Management Institute Bauer College of Business University of Houston I. IntroDuction The events of late‐summer, 2008 through the spring of 2009 have attracted considerable attention to the performance of oil price benchmarks, most notably the Chicago Mercantile Exchange’s West Texas Intermediate crude oil contract (“WTI” or “CL” hereafter) and ICE Futures’ Brent crude oil contract (“Brent futures” or “CB” hereafter). In particular, the behavior of spreads between the prices of futures contracts of different maturities, and between futures prices and cash prices during the period following the Lehman Brothers collapse has sparked allegations that futures prices have become disconnected from the underlying cash market fundamentals. The WTI contract has been the subject of particular criticisms alleging the unrepresentativeness of the Midcontinent market as a global price benchmark. I have analyzed extensive data from the crude oil cash and futures markets to evaluate the performance of the WTI and Brent futures contracts during the LH2008‐FH2009 period. Although the analysis focuses on this period, it relies on data extending back to 1990 in order to put the performance in historical context. I have also incorporated some data on physical crude market fundamentals, most 1 notably stocks, as these are essential in providing an evaluation of contract performance and the relation between pricing and fundamentals. My conclusions are as follows: 1. The October, 2008‐March 2009 period was one of historically unprecedented volatility. By a variety of measures, volatility in this period was extremely high, even compared to the months surrounding the First Gulf War, previously the highest volatility period in the modern oil trading era.
    [Show full text]
  • Sales Representatives Manual 2020
    Sales Representatives Manual Volume 4 2020 Volume 4 Table of Contents Chapter 1 Overview of Derivatives Transactions ………… 1 Chapter 2 Products of Derivatives Transactions ……………99 Derivatives Transactions and Chapter 3 Articles of Association and ……………… 165 Various Rules of the Association Exercise (Class-1 Examination) ……………………………………… 173 Chapter 1 Overview of Derivatives Transactions Introduction ∙∙∙∙∙∙∙∙ 3 Section 1. Fundamentals of Derivatives Transactions ∙∙∙∙∙∙∙∙ 10 1.1 What Are Derivatives Transactions? ∙∙∙∙∙∙∙∙ 10 Section 2. Futures Transactions ∙∙∙∙∙∙∙∙ 10 2.1 What Are Futures Transactions? ∙∙∙∙∙∙∙∙ 10 2.2 Futures Price Formation ∙∙∙∙∙∙∙∙ 14 2.3 How to Use Futures Transactions ∙∙∙∙∙∙∙∙ 17 Section 3. Forward Transactions ∙∙∙∙∙∙∙∙ 24 3.1 What Are Forward Transactions? ∙∙∙∙∙∙∙∙ 24 Section 4. Option Transactions ∙∙∙∙∙∙∙∙ 25 4.1 What Are Options Transactions? ∙∙∙∙∙∙∙∙ 25 4.2 Options’ Price Formation ∙∙∙∙∙∙∙∙ 32 4.3 Characteristics of Options Premiums ∙∙∙∙∙∙∙∙ 36 4.4 Sensitivity of Premiums to the Respective Factors ∙∙∙∙∙∙∙∙ 38 4.5 How to Use Options ∙∙∙∙∙∙∙∙ 46 4.6 Option Pricing Theory ∙∙∙∙∙∙∙∙ 57 Section 5. Swap Transactions ∙∙∙∙∙∙∙∙ 63 5.1 What Are Swap Transactions? ∙∙∙∙∙∙∙∙ 63 Section 6. Risks in Derivatives Transactions ∙∙∙∙∙∙∙∙ 72 Conclusion ∙∙∙∙∙∙∙∙ 82 Introduction Introduction 1. History of Derivatives Transactions Chapter 1 The term “derivatives” is used for financial instruments that “derive” from financial assets, meaning those that have securities such as shares or bonds as their underlying assets or financial transactions that use a reference indicator such as interest rates or exchange rates. Today the term “derivative” is used widely throughout society and not just on the financial markets. Although there has been criticism that they amplify financial risks and have a harmful impact on the Chapter 2 economy, derivatives are an indispensable requirement in supporting finance in the present age, and have become accepted as the leading edge of financial innovation.
    [Show full text]
  • Energy-Related Commodity Futures
    Universit¨atUlm Institut f¨urFinanzmathematik Energy-Related Commodity Futures Statistics, Models and Derivatives Dissertation zur Erlangung des Doktorgrades Dr. rer. nat. der Fakult¨at f¨urMathematik und Wirtschaftswissenschaften an der Universit¨at Ulm RSITÄT V E U I L N M U · · S O C I D E N N A D R O U · C · D O O C D E N vorgelegt von Dipl.-Math. oec. Reik H. B¨orger, M. S. Ulm, Juni 2007 ii . iii . Amtierender Dekan: Professor Dr. Frank Stehling 1. Gutachter: Professor Dr. R¨udiger Kiesel, Universit¨at Ulm 2. Gutachter: Professor Dr. Ulrich Rieder, Universit¨atUlm 3. Gutachter: Professor Dr. Ralf Korn, Universit¨at Kaiserslautern Tag der Promotion: 15.10.2007 iv Acknowledgements This thesis would not have been possible without the financial and scientific support by EnBW Trading GmbH. In particular, I received instructive input from Dr. Gero Schindlmayr. He suggested many of the problems that have been covered in this work. In numerous discussions he gave insight into physical and financial details of commodities and commodity markets. I also benefited from his suggestions on aspects of the mathematical models and their applicability to practical questions. I take the opportunity to thank my academic advisor Professor Dr. R¨udiger Kiesel who initiated the collaboration with EnBW from the university’s side and who supported my studies in every possible respect. I highly appreciate his confidence in my work and his encouragement which resulted in an enjoyable working environment that goes far beyond the usual conditions. I thank the members of the Institute of Financial Mathematics at Ulm University, in particular Gregor Mummenhoff, Clemens Prestele and Matthias Scherer, for the many mathematical and non-mathematical activities that enriched my time in Ulm.
    [Show full text]