DOCSLIB.ORG

Penrose Tiling.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Penrose Tiling.Pdf Andrew Glassner’s Notebook http://www.research.microsoft.com/research/graphics/glassner Penrose Tiling ______________________________________ Andrew heme and variation are part of nature. Birdwatch- translated copies of a single, larger piece. If you can do Glassner Ters identify the species of a bird by its distinctive this, then the overall pattern—and the set of tiles used markings, even though the specific colors and shapes to make it— are periodic. Microsoft vary from one bird to the next. Every thunderclap If you can’t find such a single, big piece that replicates Research sounds roughly like thunder, but each one is different. the pattern by translation, the pattern is called nonpe- And of course snowflakes are beloved for the hexagonal riodic. Many tiles can create both periodic and nonperi- symmetry they all share, as well as the delicate patterns odic patterns, depending on how they’re laid down. unique to each one. If you happen to have a set of tiles that can only make In the May/June 1998 issue of IEEE CG&A I discussed nonperiodic patterns, and you can prove that’s the case, the topic of aperiodic tiling for the plane. This technique then you have an aperiodic set of tiles. helps us create patterns with lots of theme and varia- The quest for aperiodic tiles has gone on for several tion, like the leaves on a tree. I’ll continue discussing the decades. The first set discovered involved 26,000 tiles. subject, so let’s first briefly summarize the main ideas In the last issue I discussed two far smaller sets of ape- from last time. riodic tiles, named after their creators. These Robinson The basic approach is to take a bunch of 2D shapes and Ammann tiles are based on squares, which make and impose rules on how they can connect, like the them very convenient for computer graphics applica- pieces of a jigsaw puzzle. Suppose that you have an infi- tions like texture mapping and sampling. Here I’ll look nite supply of these shapes, or tiles, and you cover the at perhaps the most famous set of aperiodic tiles, dis- plane with them, out to infinity in all directions. You covered by Roger Penrose. Actually, Penrose found two might be able to find a region of the pattern that you distinct sets of aperiodic tiles, one called “kites and could pick up and use as a rubber stamp, and by stamp- darts” and the other called “rhombs.” Each set is made ing it out an infinite number of times (without rotating of only two tiles. Let’s look at the kites and darts first. or scaling it), fill the plane with the identical design that you started with. So in essence you’ve reduced the orig- Aperiodicity inal set of pieces and their interlocking rules to just many Figure 1 shows Penrose’s kite and dart. The “kite” (the larger tile) and the “dart” (the smaller, pointed one) may be assembled only by placing them so that edges of sim- φ 1 The geome- ilar length are adjacent and the colored bands are con- θ θ θ 2 1 try of the 2 1 φ tinuous. (The names kite and dart, and this decoration Penrose kite 1 of the tiles, are due to John Conway.) Figure 2 shows an 6θ 1 and dart (a), φ 4θ φ2 example of a pattern created by these tiles. φ and a decora- φ 1 As you can see, these tiles are indeed aperiodic. A full 1 1 φ tion that forces θ proof would take more room than I have, but a gener- the matching 2θ 2θ al outline of the approach conveys most of the key ideas. φ rules (b) . I’ll use a construction technique that’s based on substi- φ=(1+√5 )/2. (a) (b) tution rules. Like the rules of a formal grammar in com- θ=36 degrees. puter science, or an L system used in botanical simulations, I’ll take each tile and replace it, in position, with another set of tiles. 2 A pattern Let’s simplify the problem for a moment and look just created by at 1D patterns. Penrose kites Suppose that you had an infinite string, and you want- and darts. (a) ed to fill it up with an aperiodic pattern of white and With kites and black beads. I’ll use two production rules to do the job. darts outlined. First, every white bead will be replaced with one white (b) Just the and two black beads in that order. I write this W→WBB, decoration. as shown in Figure 3a. Similarly, we’ll replace each black (a) (b) bead with the rule B→BWW, as in Figure 3b. 78 July/August 1998 . Let’s start with a single white bead and then apply these rules to start filling up the string. Figure 3c shows 3 Creating an (a) the first few steps. Each time you apply the rules, you aperiodic bead take the original string of beads and apply all the rules sequence. at once. So the first generation is simply WBB. Now the (a) The rule (b) new W goes to WBB, and each of the two Bs indepen- W→WBB, dently go to BWW, giving us the new string WBBB- (b) the rule WWBWW. Let’s run the process forever, so that we have B→BWW, and (theoretically) filled up the infinite string with beads. (c) three steps If the pattern generated this way is periodic, then we starting with a could find some chunk of beads—perhaps short, perhaps white bead. enormously long—that repeats. We could then take one (c) of these chunks and glue it together into a super bead, and then match the original pattern by simply filling another string with an infinite number of copies of this single super bead. If we can’t find such a super bead, the pattern is either nonperiodic or aperiodic. You 4 (a) Deflating might be able to convince yourself a kite turns it that in this example we would never (a) into two kites be able to find such a super bead. and a dart. We follow a similar process in 2D (b) Deflating a for Penrose tiles. The technique is dart turns it into typically called deflation since the a kite and two new tiles are smaller (or deflated) half-darts. versions of their predecessors. Figure 4 shows the deflation rules for the kite and the dart. Notice that two of the newly created darts in the dart (b) rule fall off the side of the tile. The matching rules come to the rescue here—you can prove that each half- tile is exactly completed by each of its legal neighbors when that neighbor 5 A Penrose tile is deflated. If you run the process “Ace” deflated back the other way and reduce the four times. number of tiles in a tiling, it’s called inflation, since each tile gets bigger. Figure 5 shows a few deflation steps applied to a small starting pat- tern of Penrose tiles. You may notice that some config- urations of tiles seem to appear sev- eral times in these tilings. This is because you can only assemble tiles around a vertex in a limited number of ways. For example, take the ver- 6 The atlas for tex at the tip of the dart and enu- kites and darts. merate all the ways that other kites Sun and Star and darts can be assembled around (top); Ace and that vertex while obeying the Deuce (middle); matching rules. Then repeat the and Jack, process for the other vertices on the Queen, and dart, and then for the kite. King (bottom). If you run through this process and eliminate duplicates, you’ll find that only seven different kinds of clusters can be formed. These clus- ters taken together are called the atlas of the tiling. Figure 6 shows the atlas for the Penrose kites and darts. IEEE Computer Graphics and Applications 79 . Andrew Glassner’s Notebook C C this limerick (the third line is kind K G K G of clunky, but let’s overlook that). The major problem here is that you J F J F just can’t rhyme with orange— B B you’re stuck and it’s nobody’s fault. I E H D You just have to back up a line or two and try again. H D I E Analytic It’s the same thing with building 7 A A expressions for Penrose tilings. You can follow all vertices in the Sun: Jack: the rules and find yourself unable to Sun and Jack. In A (0,0) A (0,0) add any more tiles. You need to take these expres- B (0, φ) B (0, k) some tiles away and try again, in a sions, k2 = 1 + φ2 C (0, φ + k) C (0, φ +k) trial-and-error process. Obviously if − 2φcos(2π/5). D (cos (π/10), sin (π/10)) D φ (cos (3π/10), sin (3π/10)) we want to create and use Penrose E φ (sin (2π/5), 1 − cos (2π/5)) E k(cos (π/10), sin (π/10)) tilings regularly we need a more reli- F k(sin (2π/5), φ + cos (2π/5)) F (φ cos (π/10), k + φsin (π/10)) able approach for generating the G (cos (π/10), φ + k −sin (π/10)) G (cos (π/10), φ+k −sin (π/10)) patterns. H (−cos (π/10), sin (π/10)) H φ (−cos (3π/10), sin (3π/10)) We saw one approach above: start I φ (−sin (2π/5), 1− cos (2π/5)) I k(−cos (π/10), sin (π/10)) with a single tile and deflate it over J k(−sin (2π/5), φ + cos (2π/5)) J (−φ cos (π/10), k + φsin (π/10)) and over, producing an ever denser K (−cos (π/10), φ +k −sin (π/10)) K (−cos (π/10), φ+ k − sin (π/10)) (or ever larger) tiling.
Load more

Recommended publications
  • ON a PROOF of the TREE CONJECTURE for TRIANGLE TILING BILLIARDS Olga Paris-Romaskevich
    ON A PROOF OF THE TREE CONJECTURE FOR TRIANGLE TILING BILLIARDS Olga Paris-Romaskevich To cite this version: Olga Paris-Romaskevich. ON A PROOF OF THE TREE CONJECTURE FOR TRIANGLE TILING BILLIARDS. 2019. hal-02169195v1 HAL Id: hal-02169195 https://hal.archives-ouvertes.fr/hal-02169195v1 Preprint submitted on 30 Jun 2019 (v1), last revised 8 Oct 2019 (v3) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. ON A PROOF OF THE TREE CONJECTURE FOR TRIANGLE TILING BILLIARDS. OLGA PARIS-ROMASKEVICH To Manya and Katya, to the moments we shared around mathematics on one winter day in Moscow. Abstract. Tiling billiards model a movement of light in heterogeneous medium consisting of homogeneous cells in which the coefficient of refraction between two cells is equal to −1. The dynamics of such billiards depends strongly on the form of an underlying tiling. In this work we consider periodic tilings by triangles (and cyclic quadrilaterals), and define natural foliations associated to tiling billiards in these tilings. By studying these foliations we manage to prove the Tree Conjecture for triangle tiling billiards that was stated in the work by Baird-Smith, Davis, Fromm and Iyer, as well as its generalization that we call Density property.
    [Show full text]
  • Tiles of the Plane: 6.891 Final Project
    Tiles of the Plane: 6.891 Final Project Luis Blackaller Kyle Buza Justin Mazzola Paluska May 14, 2007 1 Introduction Our 6.891 project explores ways of generating shapes that tile the plane. A plane tiling is a covering of the plane without holes or overlaps. Figure 1 shows a common tiling from a building in a small town in Mexico. Traditionally, mathematicians approach the tiling problem by starting with a known group of symme- tries that will generate a set of tiles that maintain with them. It turns out that all periodic 2D tilings must have a fundamental region determined by 2 translations as described by one of the 17 Crystallographic Symmetry Groups [1]. As shown in Figure 2, to generate a set of tiles, one merely needs to choose which of the 17 groups is needed and create the desired tiles using the symmetries in that group. On the other hand, there are aperiodic tilings, such as Penrose Tiles [2], that use different sets of generation rules, and a completely different approach that relies on heavy math like optimization theory and probability theory. We are interested in the inverse problem: given a set of shapes, we would like to see what kinds of tilings can we create. This problem is akin to what a layperson might encounter when tiling his bathroom — the set of tiles is fixed, but the ways in which the tiles can be combined is unconstrained. In general, this is an impossible problem: Robert Berger proved that the problem of deciding whether or not an arbitrary finite set of simply connected tiles admits a tiling of the plane is undecidable [3].
    [Show full text]
  • Simple Rules for Incorporating Design Art Into Penrose and Fractal Tiles
    Bridges 2012: Mathematics, Music, Art, Architecture, Culture Simple Rules for Incorporating Design Art into Penrose and Fractal Tiles San Le SLFFEA.com [email protected] Abstract Incorporating designs into the tiles that form tessellations presents an interesting challenge for artists. Creating a viable M.C. Escher-like image that works esthetically as well as functionally requires resolving incongruencies at a tile’s edge while constrained by its shape. Escher was the most well known practitioner in this style of mathematical visualization, but there are significant mathematical objects to which he never applied his artistry including Penrose Tilings and fractals. In this paper, we show that the rules of creating a traditional tile extend to these objects as well. To illustrate the versatility of tiling art, images were created with multiple figures and negative space leading to patterns distinct from the work of others. 1 1 Introduction M.C. Escher was the most prominent artist working with tessellations and space filling. Forty years after his death, his creations are still foremost in people’s minds in the field of tiling art. One of the reasons Escher continues to hold such a monopoly in this specialty are the unique challenges that come with creating Escher type designs inside a tessellation[15]. When an image is drawn into a tile and extends to the tile’s edge, it introduces incongruencies which are resolved by continuously aligning and refining the image. This is particularly true when the image consists of the lizards, fish, angels, etc. which populated Escher’s tilings because they do not have the 4-fold rotational symmetry that would make it possible to arbitrarily rotate the image ± 90, 180 degrees and have all the pieces fit[9].
    [Show full text]
  • Robotic Fabrication of Modular Formwork for Non-Standard Concrete Structures
    Robotic Fabrication of Modular Formwork for Non-Standard Concrete Structures Milena Stavric1, Martin Kaftan2 1,2TU Graz, Austria, 2CTU, Czech Republic 1www. iam2.tugraz.at, 2www. iam2.tugraz.at [email protected], [email protected] Abstract. In this work we address the fast and economical realization of complex formwork for concrete with the advantage of industrial robot arm. Under economical realization we mean reduction of production time and material efficiency. The complex form of individual formwork parts can be in our case double curved surface of complex mesh geometry. We propose the fabrication of the formwork by straight or shaped hot wire. We illustrate on several projects different approaches to mould production, where the proposed process demonstrates itself effective. In our approach we deal with the special kinds of modularity and specific symmetry of the formwork Keywords. Robotic fabrication; formwork; non-standard structures. INTRODUCTION Figure 1 Designing free-form has been more possible for Robot ABB I140. architects with the help of rapidly advancing CAD programs. However, the skin, the facade of these building in most cases needs to be produced by us- ing costly formwork techniques whether it’s made from glass, concrete or other material. The problem of these techniques is that for every part of the fa- cade must be created an unique mould. The most common type of formwork is the polystyrene (EPS or XPS) mould which is 3D formed using a CNC mill- ing machine. This technique is very accurate, but it requires time and produces a lot of waste material. On the other hand, the polystyrene can be cut fast and with minimum waste by heated wire, especially systems still pertinent in the production of archi- when both sides of the cut foam can be used.
    [Show full text]
  • Pentaplexity: Comparing Fractal Tilings and Penrose Tilings
    Introducing Fractal Penrose Tilings Introducing Penrose’s Original Pentaplexity Tiling Comparing Fractal Tiling and Pentaplexity Tiling Pentaplexity: Comparing fractal tilings and Penrose tilings Adam Brunell and Daniel Sherwood Vassar College [email protected] [email protected] | April 6, 2013 Adam Brunell and Daniel Sherwood Penrose Fractal Tilings Introducing Fractal Penrose Tilings Introducing Penrose’s Original Pentaplexity Tiling Comparing Fractal Tiling and Pentaplexity Tiling Overview 1 Introducing Fractal Penrose Tilings 2 Introducing Penrose’s Original Pentaplexity Tiling 3 Comparing Fractal Tiling and Pentaplexity Tiling Adam Brunell and Daniel Sherwood Penrose Fractal Tilings Introducing Fractal Penrose Tilings Introducing Penrose’s Original Pentaplexity Tiling Comparing Fractal Tiling and Pentaplexity Tiling Penrose’s Kites and Darts Adam Brunell and Daniel Sherwood Penrose Fractal Tilings Introducing Fractal Penrose Tilings Introducing Penrose’s Original Pentaplexity Tiling Comparing Fractal Tiling and Pentaplexity Tiling Drawing the Aorta in Kites and Darts Adam Brunell and Daniel Sherwood Penrose Fractal Tilings Introducing Fractal Penrose Tilings Introducing Penrose’s Original Pentaplexity Tiling Comparing Fractal Tiling and Pentaplexity Tiling Fractal Penrose Tiling Adam Brunell and Daniel Sherwood Penrose Fractal Tilings Introducing Fractal Penrose Tilings Introducing Penrose’s Original Pentaplexity Tiling Comparing Fractal Tiling and Pentaplexity Tiling Fractal Tile Set Adam Brunell and Daniel Sherwood Penrose
    [Show full text]
  • How to Make a Penrose Tiling
    How to make a Penrose tiling A tiling is a way to cover a flat surface using a fixed collection of shapes. In the left-hand picture the tiles are rectangles, while in the right- hand picture they are octagons and squares. You have probably seen many different tilings around your home or in the streets! In each of these examples, you could draw the tiling pattern on tracing paper and then shift the paper so that the lines once again match up with the tiles. Mathematicians wondered whether it was possible to make a tiling which didn’t have this property: a tiling where the tracing paper would never match the pattern again, no matter how far you moved it or in which direction. Such a tiling is called aperiodic and there are actually many examples of them. The most famous example of an aperiodic tiling is called a Penrose tiling, named after the mathematician and physicist Roger Penrose. A Penrose tiling uses only two shapes, with rules on how they are allowed to go together. These shapes are called kites and darts, and in the version given here the red dots have to line up when the shapes are placed next to each other. This means, for example, that the dart cannot sit on top of the kite. Three possible ways Kite Dart to start a Penrose tiling are given below: they are called the ‘star’, ‘sun’ and ‘ace’ respectively. There are 4 other ways to arrange the tiles around a point: can you find them all? (Answer on the other side!) Visit mathscraftnz.org | Tweet to #mathscraftnz | Email [email protected] Here are the 7 ways to fit the tiles around a point.
    [Show full text]
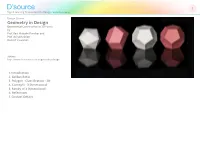
  • Geometry in Design Geometrical Construction in 3D Forms by Prof
    D’source 1 Digital Learning Environment for Design - www.dsource.in Design Course Geometry in Design Geometrical Construction in 3D Forms by Prof. Ravi Mokashi Punekar and Prof. Avinash Shide DoD, IIT Guwahati Source: http://www.dsource.in/course/geometry-design 1. Introduction 2. Golden Ratio 3. Polygon - Classification - 2D 4. Concepts - 3 Dimensional 5. Family of 3 Dimensional 6. References 7. Contact Details D’source 2 Digital Learning Environment for Design - www.dsource.in Design Course Introduction Geometry in Design Geometrical Construction in 3D Forms Geometry is a science that deals with the study of inherent properties of form and space through examining and by understanding relationships of lines, surfaces and solids. These relationships are of several kinds and are seen in Prof. Ravi Mokashi Punekar and forms both natural and man-made. The relationships amongst pure geometric forms possess special properties Prof. Avinash Shide or a certain geometric order by virtue of the inherent configuration of elements that results in various forms DoD, IIT Guwahati of symmetry, proportional systems etc. These configurations have properties that hold irrespective of scale or medium used to express them and can also be arranged in a hierarchy from the totally regular to the amorphous where formal characteristics are lost. The objectives of this course are to study these inherent properties of form and space through understanding relationships of lines, surfaces and solids. This course will enable understanding basic geometric relationships, Source: both 2D and 3D, through a process of exploration and analysis. Concepts are supported with 3Dim visualization http://www.dsource.in/course/geometry-design/in- of models to understand the construction of the family of geometric forms and space interrelationships.
    [Show full text]
  • A Game of Life on Penrose Tilings
    A Game of Life on Penrose Tilings Kathryn Lindsey Department of Mathematics Cornell University Olivetti Club, Sept. 1, 2009 Outline 1 Introduction Tiling definitions 2 Conway’s Game of Life 3 The Projection Method Wikipedia: “...Almost all metal exists in a polycristalline state.” “A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions.” Is there a way to encode/process information in a nonperiodic environment? Our technology for dealing with information is restricted to materials with periodic structures. “A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions.” Is there a way to encode/process information in a nonperiodic environment? Our technology for dealing with information is restricted to materials with periodic structures. Wikipedia: “...Almost all metal exists in a polycristalline state.” Is there a way to encode/process information in a nonperiodic environment? Our technology for dealing with information is restricted to materials with periodic structures. Wikipedia: “...Almost all metal exists in a polycristalline state.” “A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions.” Our technology for dealing with information is restricted to materials with periodic structures. Wikipedia: “...Almost all metal exists in a polycristalline state.” “A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions.” Is there a way to encode/process information in a nonperiodic environment? A tiling of the plane is a partition of the plane into sets (called tiles) that are topological disks.
    [Show full text]
  • Collection Volume I
    Collection volume I PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Thu, 29 Jul 2010 21:47:23 UTC Contents Articles Abstraction 1 Analogy 6 Bricolage 15 Categorization 19 Computational creativity 21 Data mining 30 Deskilling 41 Digital morphogenesis 42 Heuristic 44 Hidden curriculum 49 Information continuum 53 Knowhow 53 Knowledge representation and reasoning 55 Lateral thinking 60 Linnaean taxonomy 62 List of uniform tilings 67 Machine learning 71 Mathematical morphology 76 Mental model 83 Montessori sensorial materials 88 Packing problem 93 Prior knowledge for pattern recognition 100 Quasi-empirical method 102 Semantic similarity 103 Serendipity 104 Similarity (geometry) 113 Simulacrum 117 Squaring the square 120 Structural information theory 123 Task analysis 126 Techne 128 Tessellation 129 Totem 137 Trial and error 140 Unknown unknown 143 References Article Sources and Contributors 146 Image Sources, Licenses and Contributors 149 Article Licenses License 151 Abstraction 1 Abstraction Abstraction is a conceptual process by which higher, more abstract concepts are derived from the usage and classification of literal, "real," or "concrete" concepts. An "abstraction" (noun) is a concept that acts as super-categorical noun for all subordinate concepts, and connects any related concepts as a group, field, or category. Abstractions may be formed by reducing the information content of a concept or an observable phenomenon, typically to retain only information which is relevant for a particular purpose. For example, abstracting a leather soccer ball to the more general idea of a ball retains only the information on general ball attributes and behavior, eliminating the characteristics of that particular ball.
    [Show full text]
  • A Class of Spherical Penrose-Like Tilings with Connections to Virus Protein Patterns and Modular Sculpture
    Bridges 2018 Conference Proceedings A Class of Spherical Penrose-Like Tilings with Connections to Virus Protein Patterns and Modular Sculpture Hamish Todd Center for Synthetic and Systems Biology, University of Edinburgh, UK; [email protected] Abstract The focus of this paper is a class of symmetrically patterned spherical polyhedra we call “Twarock-Konevtsova” (T-K) tilings, which were first applied to the study of viruses. We start by defining the more general concept of a “wrapping paper pattern,” and T-K tilings (along with one other virus tiling) are outlined as a subset of them. T-K tilings are then considered as “spherical Penrose tilings” and a pair of algorithms for generating them is described. We believe they present good source material for mathematical sculpture, especially modular origami, having intriguing features such as consistent edge lengths and a limited selection of angles in their constituent faces. We conclude by looking at existing examples of T-K tilings in mathematical sculpture and consider different directions they could be taken in. Introduction Symmetrically patterned spherical polyhedra, discovered by geometers, have inspired artists across many cultures [4]. This may well be because, in addition to their aesthetic appeal, they have “structural” benefits: spheres are very stable, and objects with patterns on them, being made of a limited set of repeated pieces, are generally “simple” to construct. For example, the origamist who made the object in Figure 9d only needed to make copies of one simple module and then slot them together. If that same origamist were to make a sculpture of equal size and intricacy but without following a pattern, it would have to involve coordination of different things.
    [Show full text]
  • Arxiv:1205.5118V2 [Math.MG] 12 Nov 2013 Berger [4] Proved That the Problem to Know Whether Or Not ΩP Is Empty (I.E
    TILINGS OF THE PLANE AND THURSTON SEMI-NORM JEAN-RENE´ CHAZOTTES, JEAN-MARC GAMBAUDO, AND FRANC¸OIS GAUTERO Abstract. We show that the problem of tiling the Euclidean plane with a finite set of polygons (up to translation) boils down to prove the existence of zeros of a non-negative convex function defined on a finite-dimensional simplex. This function is a generalisation, in the framework of branched surfaces, of the Thurston semi-norm originally defined for compact 3-manifolds. 1. Introduction Consider a finite collection P “ tp1; : : : ; pnu, where for j “ 1; : : : ; n, pj is a polygon in the Euclidean plane R2, indexed by j and with colored edges. These decorated polygons are called prototiles. In the sequel a rational prototile (resp. integral prototile) is a prototile whose vertices have rational (resp. integer) coordi- 2 nates. A tiling of R made with P is a collection ptiqi¥0 of polygons called tiles indexed by a symbol kpiq in t1; : : : ; nu, such that: 2 ‚ the tiles cover the plane: Yi¥0ti “ R ; ‚ the tiles have disjoint interiors: intptiq X intptjq “ H whenever i ‰ j; ‚ whenever two distinct tiles intersect, they do it along a common edge and the colors match; ‚ for each i ¥ 0, ti is a translated copy of pkpiq. We denote by ΩP the set of all tilings made with P. Clearly this set may be empty. When ΩP ‰H the group of translation acts on ΩP as follows: 2 ΩP ˆ R Q pT; uq ÞÑ T ` u P ΩP where T `u “ pti `uqi¥0 whenever T “ ptiqi¥0.
    [Show full text]
  • Penrose Tiles and Aperiodic Tessellations
    Penrose Tiles and Aperiodic Tessellations Penrose tilings are a remarkable example of aperiodic, semi-regular tessellations1. What follows is an excerpt from an article on Penrose tilings by Martin Gardner, from his book “Penrose Tiles to Trapdoor Ciphers”. Gardner was the long-time author of a mathematics column in Scientific American magazine, as well as author of many books. He, more than anyone else, has made major contributions to making deep mathematics accessible to general audiences. His work demonstrates that, much like one need not be a Yeats scholar to appreciate and understand poetry, one need not be a professional mathematician to appreciate, understand, and find beauty and value in mathematics. This short excerpt covers many of the ideas we talked briefly about in class and illustrates them with pictures and examples. 1exercise: define all of the technical terms in that sentence! 1 Penr ose Tiling At the end of a 1975 Scientific American column on tiling the plane periodically with congruent convex polygons (reprinted in my Time Travel and Other Mathematical Bewilderments) I promised a later column on nonperiodic tiling. This chapter reprints my fulfillment of that promise -a 1977 column that reported for the first time a remark- able nonperiodic tiling discovered by Roger Penrose, the noted British mathematical physicist and cosmologisr. First, let me give some defini- tions and background. A periodic tiling is one on which you can outline a region that tiles the plane by translation, that is, by shifting the position of the region without rotating or reflecting it. M. C. Escher, the Dutch artist, is famous for his many pictures of periodic tilings with shapes that resemble living things.
    [Show full text]