Applying Greedy Genetic Algorithm on 0/1 Multiple Knapsack Problem
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

UNIVERSITY GRANTS COMMISSION State-Wise List of Private
UNIVERSITY GRANTS COMMISSION State-wise List of Private Universities as on 01.02.2020 S.No Name of Private University Date of Notification ARUNACHAL PRADESH 1. Apex Professional University, Pasighat, District East Siang, 10.05.2013 Arunachal Pradesh - 791102. 2. Arunachal University of Studies, NH-52, Namsai, Distt – Namsai 26.05.2012 - 792103, Arunachal Pradesh. 3. Arunodaya University, E-Sector, Nirjuli, Itanagar, Distt. Papum 21.10.2014 Pare, Arunachal Pradesh-791109 4. Himalayan University, 401, Takar Complex, Naharlagun, 03.05.2013 Itanagar, Distt – Papumpare – 791110, Arunachal Pradesh. 5. North East Frontier Technical University, Sibu-Puyi, Aalo 03.09.2014 (PO), West Siang (Distt.), Arunachal Pradesh –791001. 6. The Global University, Hollongi, Itanagar, Arunachal Pradesh. 18.09.2017 7. The Indira Gandhi Technological & Medical Sciences University, 26.05.2012 Ziro, Arunachal Pradesh. 8. Venkateshwara Open University, Itanagar, Arunachal Pradesh. 20.06.2012 S.No Andhra Pradesh 9. Bharatiya Engineering Science and Technology Innovation 17.02.2019 University, Gownivaripalli, Gorantla Mandal, Anantapur, Andhra Pradesh 10. Centurian University of Technology and Management, Gidijala 23.05.2017 Junction, Anandpuram Mandal, Visakhapatnam- 531173, Andhra Pradesh. 11. KREA University, 5655, Central, Expressway, Sri City-517646, 30.04.2018 Andhra Pradesh 12. Saveetha Amaravati University, 3rd Floor, Vaishnavi Complex, 30.04.2018 Opposite Executive Club, Vijayawada- 520008, Andhra Pradesh 13. SRM University, Neerukonda-Kuragallu Village, mangalagiri 23.05.2017 Mandal, Guntur, Dist- 522502, Andhra Pradesh (Private University) 14. VIT-AP University, Amaravati- 522237, Andhra Pradesh (Private 23.05.2017 University) ASSAM 15. Assam Don Bosco University, Azara, Guwahati 12.02.2009 16. Assam Down Town University, Sankar Madhab Path, Gandhi 29.04.2010 Nagar, Panikhaiti, Guwahati – 781 036. -

Consolidated List Private Universities
UNIVERSITY GRANTS COMMISSION State-wise List of Private Universities as on 06.08.2021 S.No Name of Private University Date of Notification ARUNACHAL PRADESH 1. Apex Professional University, Pasighat, District East Siang, 10.05.2013 Arunachal Pradesh - 791102. 2. Arunachal University of Studies, NH-52, Namsai, Distt – Namsai 26.05.2012 - 792103, Arunachal Pradesh. 3. Arunodaya University, E-Sector, Nirjuli, Itanagar, Distt. Papum 21.10.2014 Pare, Arunachal Pradesh-791109 4. Himalayan University, 401, Takar Complex, Naharlagun, 03.05.2013 Itanagar, Distt – Papumpare – 791110, Arunachal Pradesh. 5. North East Frontier Technical University, Sibu-Puyi, Aalo 03.09.2014 (PO), West Siang (Distt.), Arunachal Pradesh –791001. 6. The Global University, Hollongi, Itanagar, Arunachal Pradesh. 18.09.2017 7. The Indira Gandhi Technological & Medical Sciences University, 26.05.2012 Ziro, Arunachal Pradesh. 8. Venkateshwara Open University, Itanagar, Arunachal Pradesh. 20.06.2012 Andhra Pradesh 9. Bharatiya Engineering Science and Technology Innovation 17.02.2019 University, Gownivaripalli, Gorantla Mandal, Anantapur, Andhra Pradesh 10. Centurian University of Technology and Management, Gidijala 23.05.2017 Junction, Anandpuram Mandal, Visakhapatnam- 531173, Andhra Pradesh. 11. KREA University, 5655, Central, Expressway, Sri City-517646, 30.04.2018 Andhra Pradesh 12. Saveetha Amaravati University, 3rd Floor, Vaishnavi Complex, 30.04.2018 Opposite Executive Club, Vijayawada- 520008, Andhra Pradesh 13. SRM University, Neerukonda-Kuragallu Village, mangalagiri 23.05.2017 Mandal, Guntur, Dist- 522502, Andhra Pradesh (Private University) 14. VIT-AP University, Amaravati- 522237, Andhra Pradesh (Private 23.05.2017 University) ASSAM 15. Assam Don Bosco University, Azara, Guwahati 12.02.2009 16. Assam Down Town University, Sankar Madhab Path, Gandhi 29.04.2010 Nagar, Panikhaiti, Guwahati – 781 036. -

Details of Top Institute/University from Where Students Admitted to Our University for Higher Studies (5D) Admitted in 2017 Sr
Details of Top Institute/University from where Students admitted to our University for higher studies (5D) Admitted in 2017 Sr. Name Name of Graduating Year of Program No. University/Institute From Year Admission (M.Tech/PhD) where graduated 1 Guru Govind Singh 2013 2017 M.Tech(ME) Ashok Kumar University,Delhi . 2 Bhavesh MDU,Rohtak 2015 2017 M.Tech(ME) Singhal 3 Bhupender MDU,Rohtak 2013 2017 M.Tech(ME) Singh 4 Deepak MDU,Rohtak 2015 2017 M.Tech(ME) Vashishta 5 Devesh Kumar MDU,Rohtak 2013 2017 M.Tech(ME) 6 Jitender RTU, Kota 2016 2017 M.Tech(ME) 7 Kashika MDU,Rohtak 2016 2017 M.Tech(ME) Aggarwal 8 Mahesh Kumar UIET,Kurukshetra 2016 2017 M.Tech(ME) 9 Manorma GBTU,Noida 2013 2017 M.Tech(ME) 10 Parag UIET,Kurukshetra 2016 2017 M.Tech(ME) 11 Pravesh Kumar MDU,Rohtak 2014 2017 M.Tech(ME) 12 Rahul Kumar MDU,Rohtak 2016 2017 M.Tech(ME) 13 Shivraj Thakur MDU,Rohtak 2017 2017 M.Tech(ME) 14 Suman YMCAUST,Faridabad 2017 2017 M.Tech(ME) 15 Umesh Deswal MDU,Rohtak 2016 2017 M.Tech(ME) 16 Vipin Sharma MDU,Rohtak 2016 2017 M.Tech(ME) 17 Aditi Virmani MDU,Rohtak 2017 2017 M.Tech (VLSI) 18 Barkha MDU,Rohtak 2017 2017 M.Tech (VLSI) 19 Harshul MDU,Rohtak 2016 2017 M.Tech Mahendroo (VLSI) 20 Jyoti Choudhary MDU,Rohtak 2010 2017 M.Tech (VLSI) 21 Liladhar UPTU 2013 2017 M.Tech (VLSI) 22 Naveen Kumar MDU,Rohtak 2016 2017 M.Tech Dubey (VLSI) 23 Preksha Goyal MDU,Rohtak 2017 2017 M.Tech (VLSI) 24 Ravi Prakash PTU,Patiala 2014 2017 M.Tech 25(VLSI) 25 Sanskriti Gupta KUK 2016 2017 M.Tech (VLSI) 26 Vinay Goyal MDU,Rohtak 2012 2017 M.Tech (VLSI) 27 Vivek Kumar -

Department of Laws
DEPARTMENT OF LAWS Name- Dr. Pawan Kumar Designation-Assistant Professor-in-Law Date of Birth-06th November 1975 Sex-Male Specialization- Constitutional Law Educational Qualifications- Sr. No. Degree Year of Passing University/Institute 1 B.Com. 1997 Maharishi Dayanand University, Rohtak 2 LL.B. 2000 Maharishi Dayanand University, Rohtak 3 LL.M. 2003 Maharishi Dayanand University, Rohtak 4 B.J.M.C. 2004 Maharishi Dayanand University, Rohtak 5 M.M.C. 2005 Guru Jamdeshwar University of Science and Technology, Hisar 6 Ph.D. (Law) 2009 Maharishi Dayanand University, Rohtak Career Profile- Sr. Institute served Designation From To No. 1 National Institute of Law, Lecturer July 23, 2004 January 12, Faridabad 2005 2 Vivekananda Institute of Lecturer January 13, 2005 March 29, Professional Studies, New Delhi 2007 3 Faculty of Law, Kurukshetra Lecturer March 30, 2007 July 26, 2007 University, Kurukshetra 4 Department of Laws, BPS Assistant July 26, 2007 Till date Women University, Khanpur Professor Kalan, Sonepat 1 Research Advisory- Ph.D. LL.M. No. of Students Supervised Nil Nil ∙Publications- Published a research paper entitled “Indian Constitutional Law Pertaining to Reservation in Jobs under the State: A Critical Analysis” in a book entitled “Indian Constitution And Weaker Sections” edited by Dr. S.C. Sharma, Professor and Head, Department of Laws, Guru Nanak Dev University Regional Campus, Jalandhar, published by Guru Nanak Dev University, Amritsar, bearing ISBN 81-7770-130-4. Published a research paper entitled “Juvenile by Act or Appearance: Avertable Controversy Settled” in M.D.U. Law Journal, published by Department of Law, M.D. University, Rohtak, bearing ISSN 2230-746X. -

Provisional List of Physiotherapy Colleges in Haryana (Suitability Post Inspection)
HARYANA STATE COUNCIL FOR PHYSIOTHERAPY Bays No 55-58 Paryattan Bhawan 2nd Floor Sector-2, Panchkula E-mail -: [email protected] Phone Number: 0172-2930458 Provisional List of Physiotherapy Colleges in Haryana (Suitability Post Inspection) Sr. Name of Institute Status Address B.P.T. M.P.T. Ph.D. Contact No./Person No. 1. College of Physiotherapy PGIMS, Govt. Pt. B.D. Sharma P.G.I.M.S, Medical 94674-04050, 8607157000, Rohtak Rd, Rohtak, Haryana 124001 30 10 -- 01262-281307, [email protected] m 2 College of Physiotherapy, Pandit Govt. Pandit Deen Dayal Upadhayaya 80537-33016, 9997285700 Deen Dayal Upadhayaya University of Health Sciences, 30 -- -- [email protected] University of Health Science, Village Kutail, Karnal Kutail, Karnal 3. College of Physiotherapy Govt. Health Center, Guru Jambheshwar 01662-263169 Department of Physiotherapy University of Science and 50 42 2-6 97299-22466 Ms. Shabnam GJU, Hissar Technology, Hisar, Haryana Joshi 125011 Chairmanphysio2019@gmai l.com 4. Saket College of Physiotherapy, Aided Chandimandir Cantonment, NitiGautam-9501766396, Chandimandir, Panchkula ChandiMandir, Panchkula Haryana 40 15 -- 9779790707, 94162-79767, 134107 0172-2554022 [email protected] 1 | P a g e HARYANA STATE COUNCIL FOR PHYSIOTHERAPY Bays No 55-58 Paryattan Bhawan 2nd Floor Sector-2, Panchkula E-mail -: [email protected] Phone Number: 0172-2930458 5 College of Physiotherapy, Aided Agroha, Distt. Hisar Haryana 92551-86661, 9729180949, Maharaja Agresan Medical 125047 40 -- -- 01669-281193 Collage, Agroha, Hisar [email protected]. in 6 College of Physiotherapy Pvt. MMU, Mullana, Distt. Ambala 80599-30229 Maharishi Makandeshwar Haryana 133207 120 35 8 [email protected] University, Mullana rg 7 College of Physiotherapy Manav Pvt. -

Eligibility Circular No 205 of 2021 30.08.2021.Pdf
SAVITRIBAI PHULE PUNE UNIVERSITY (Formerly University of Pune) CIRCULAR No. 205 of 2021 INFORMATION REGARDING ELIGIBILITY CRITERIA FOR VARIOUS UNIVERSITY COURSES. Website : http://unipune.ac.in Dr. Nitin Karmalkar Hon’ble Vice-Chancellor, Savitribai Phule Pune University Dr. N. S. Umarani Hon’ble Pro-Vice-Chancellor, Savitribai Phule Pune University Eligibility Staff Members 1. Smt. M. S. Uttekar Asstt. Registrar Ph. : 25621180 2. Smt M. J. D’souza Asstt. Section Officer Ph. : 25621181 3. Smt. G. J. Zagade Assistant Ph. : 25621183 4. Smt. B. T. Patil Assistant Ph. : 25621182 5. Shri. B. C. Gajalwar Assistant Ph. : 25621187 INDEX Sr. No. Title Page No. 1.Circular .... 1-7 2. Course wise and yearwise No of Students Enrolled .... 8 3. Eligibility Equaivlence Letter & Government Resolution .... 9 - 19 for equivalence of I.T.I. 4. Faculty of Science and Technology 1. Science .... 20-38 2. Engineering .... 39-62 3. Technology .... 63-65 4. Architecture .... 66-67 5. Pharmaceutical Sciences .... 68-69 5. Faculty of Commerce and Management 1. Commerce .... 70-74 2. Management .... 75-78 6. Faculty of Humanities 1. Arts .... 79 - 83 2. Mental Moral & Social Sciences .... 84-89 3. Law .... 90 - 94 7. Faculty of Interdisciplinary Studies 1. Education .... 95 - 98 2. Physical Education .... 99 - 102 3. Library Science .... 103 4. Fine & Performing Arts .... 104 5. Social Work & Journalism .... 105 8. M.Phil. & Ph.D. .... 106-107 9. Definition .... 108-109 10. Instructions For the Final List of Eligibility Chart I .... 110-111 11. Annexure ‘A’ Eligibility Fee .... 112 12. Procedure for Migration Certificate Application .... 113 13. List of U.G.C Recognized University ... -

National Level Review / Interface Meeting of NAD Scheduled on 22Nd June 2018 Sl.No Name of Institution 1 Al-Falah University, Fa
National Level Review / Interface Meeting of NAD scheduled on 22nd June 2018 Sl.No Name of Institution 1 Al-Falah University, Faridabad, Haryana. Amity University, Amity Education Valley, Panchgaon, 2 Manesar, Distt. – Gurgaon-122 413, Haryana. 3 Ansal University, Gurgaon, Haryana. Apeejay Stya University, Palwal Road, Sohna, Gurgaon – 122 4 103, Haryana. Ashoka University, Plot No. 2, Rajiv Gandhi Education City, 5 Kundli, NCR, Sonepat, Haryana. (Private University) 6 Baba Mast Nath University, Rohtak, Haryana. BML Munjal University, 67th KM Stone, NH-8, Sidhrawali, 7 Dist. Gurgaon – 123 413, Haryana. G.D. Goenka University, G.D. Goenka Education City, Gurgaon 8 sohna Road, Gurgaon, Haryana – 122 103. Jagan Nath University, State Highway 22, Bahadurgarh-Jhajjar 9 Road,Jhajjar – 124 507, Haryana. K.R. Mangalam University, Sohna Road, Gurgaon, Haryana – 10 122 103. Manav Rachna University, Sector – 43, Delhi-Surajkund Road, 11 Faridabad, Haryana. 12 M.V.N. University, Palwal, Haryana. Maharashi Markandeshwar University, Sadopur, Distt. 13 Ambala, Haryana NIILM University, 9 KM Milestone, NH-65, Kaithal – 136 027, 14 Haryana. 15 O.P. Jindal Global University, Sonipat. PDM University, Post Box No. 15, Sector – 3A, Sarai 16 Aurangabad, Bahadurgarh-124507, Haryana. Shree Guru Gobind Singh Tricentenary University, Farukh 17 Nagar Road, Budhera, Distt. Gurgaon, Haryana. SRM University, Plot No. 39, Rajiv Gandhi Education City, Delhi-NCR, Sonepat-Kundli Urban Complex, Haryana – 131 18 029. Starex University, NH-8, Village – Binola, PO – Bhorakalan, 19 Gurugram, Haryana. The Northcap University, HUDA Sector 23 A, Gurgoan- 20 122107, Haryana. Abhilashi University, Chailchowk (Chachiot), Distt. Mandi, 21 Himachal Pradesh. A.P.G. (Alakh Prakash Goyal) University, Shimla, Himachal 22 Pradesh. -
Important Notes
1 IMPORTANT NOTES 1. The eligibility for admission to a particular course may be determined on the basis of equivalence shown in this list and the detailed conditions given in the Admission Brochure(s)/Information Brochure/ Prospectuses etc. and the relevant Ordinances. 2. B.A./B.Sc./B.Com/B.Sc.(Home Science) pass/honours and shastri (with English) etc. courses under 10+2+3 pattern of examinations and M.A./M.Sc./M.Com/ Acharya and LL.M. etc of two years duration after three years graduation degree or five years after +2 level examination of all the statutory Universities in India including open/private Universities/ deemed to be universities/ institutes of National Importance established by an Act of the state Govt./Centre govt. which are approved by the University Grants Commission (UGC) / Ministry of HRD have been recognized as equivalent to the respective course of this university without following the normal procedure of comparing the syllabi and scheme of examination etc. List of Universities approved by UGC is appended at Appendix ‘A’. However, updated list of such universities may be seen on UGC website (www.ugc.ac.in). List of Institute of National Importance is available at Appendix ‘B’. However, updated list of such Institutes may be seen on the website (http://mhrd.gov.in) of Ministry of HRD (Department of Higher Education Govt. of India Three-year Programme of BBA/BCA run by Universities including open/private Universities/deemed to be Universities established by an Act of the Central/State Legislature and approved by UGC are recognized as equivalent to BBA/BCA of this University. -
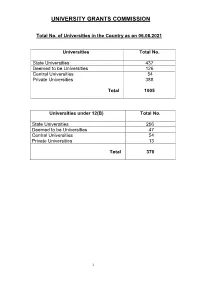
Consolidated List of All Universities
UNIVERSITY GRANTS COMMISSION Total No. of Universities in the Country as on 06.08.2021 Universities Total No. State Universities 437 Deemed to be Universities 126 Central Universities 54 Private Universities 388 Total 1005 Universities under 12(B) Total No. State Universities 256 Deemed to be Universities 47 Central Universities 54 Private Universities 13 Total 370 1 S.No ANDHRA PRADESH Date/Year of Notification/ Establishment 1. Acharya N.G. Ranga Agricultural University, Lam, 1964 Guntur – 522 034,Andhra Pradesh (State University) 2. Acharya Nagarjuna University, Nagarjuna Nagar-522510, Dt. Guntur, 1976 Andhra Pradesh. (State University) 3. Adikavi Nannaya University, 25-7-9/1, Jayakrishnapuram, 2006 Rajahmundry – 533 105, East Godavari District, Andhra Pradesh. (State University) 4. Andhra University, Waltair, Visakhapatnam-530 003, Andhra Pradesh. 1926 (State University) 5. Bharatiya Engineering Science and Technology Innovation University, 17.02.2019 Gownivaripalli, Gorantla Mandal, Anantapur, Andhra Pradesh (Private University) 6. Central University of Andhra Pradesh, IT Incubation Centre Building, 05.08.2019 JNTU Campus, Chinmaynagar, Anantapuramu, Andhra Pradesh- 515002 (Central University) 7. Central Tribal University of Andhra Pradesh, Kondakarakam, 05.08.2019 Vizianagaram, Andhra Pradesh 535008 (Central University) 8. Centurion University of Technology and Management, Gidijala Junction, 23.05.2017 Anandapuram Mandal, Visakhapatnam – 531173, Andhra Pradesh. (Private University) 9. Damodaram Sanjivayya National Law University, Plot No. 116, Sector 2008 11 MVP Colony, Visakhapatnam – 530 017, Andhra Pradesh. (State University) 10. Dr. Abdul Haq Urdu University, Kurnool- 518001, Andhra Pradesh 14.12.2018 (State University) 11. Dr. B.R. Ambedkar University, Etcherla, Dt. Srikakulam-532410, 2008 Andhra Pradesh. (State University) 12. Dravidian University, Srinivasanam, -517 425, Chittoor District, 1997 Andhra Pradesh. -
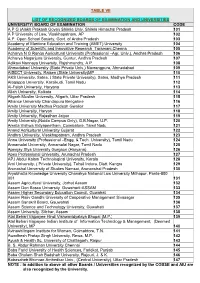
Table Vii List of Recognized Boards of Examination and Universities
TABLE VII LIST OF RECOGNIZED BOARDS OF EXAMINATION AND UNIVERSITIES UNIVERSITY/ BOARD OF EXAMINATION CODE A P G (Alakh Prakash Goyal) Shimla Univ. Shimla Himachal Pradesh 101 A P University of Law, Visakhapatnam, AP 102 A.P. Open School Society, Govt. of Andra Pradesh 103 Academy of Maritime Education and Training (AMET) University 104 Academy of Scientific and Innovative Research Taramani,Chennai 105 Acharya N G Ranga Agricultural University (Professional –Agr. Univ.), Andhra Pradesh 106 Acharya Nagarjuna University, Guntur, Andhra Pradesh 107 Adikavi Nannaya University, Rajahmundry, A.P. 108 Ahmedabad University (State Private Univ.) Navrangpura, Ahmedabad 109 AISECT University, Raisen (State University)MP 110 AKS University, Satna, ( State Private University), Satna, Madhya Pradesh 111 Alagappa University, Karaikudi, Tamil Nadu 112 Al-Falah University, Haryana 113 Aliah University, Kolkata 114 Aligarh Muslim University, Aligarh, Uttar Pradesh 115 Alliance University Chandapura Bengalore 116 Amity University Madhya Pradesh Gwalior 117 Amity University, Haryan 118 Amity University, Rajasthan Jaipur 119 Amity University,(Noida Campus Only), G.B.Nagar, U.P. 120 Amrita Vishwa Vidyapeetham, Coimbatore, Tamil Nadu 121 Anand Agricultural University Gujarat 122 Andhra University, Visakhapatnam, Andhra Pradesh 123 Anna University (Professional –Engg. & Tech. University), Tamil Nadu 124 Annamalai University, Annamalai Nagar, Tamil Nadu 125 Apeejay Stya University Gurgaon (Haryana) 126 Apex Professional University, Arunachal Pradesh 127 APJ Abdul -
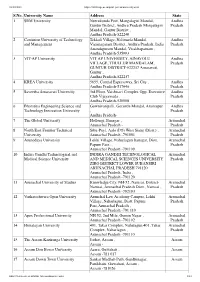
S.No. University Name
01/09/2021 https://www.ugc.ac.in/print_privateuniversity.aspx S.No. University Name Address State 1 SRM University Neerukonda Post, Mangalagiri Mandal, Andhra Guntur District, Andhra Pradesh Mangalagiri Pradesh Mandal, Gantur District , Andhra Pradesh-522240 2 Centurion University of Technology Tekkali Village, Nelimarla Mandal, Andhra and Management Vizianagaram District, Andhra Pradesh, India Pradesh Anandapuram Mandal, Visakhapatnam , Andhra Pradesh-535003 3 VIT-AP University VIT AP UNIVERSITY, AINAVOLU Andhra VILLAGE, THULLUR MANDALAM, Pradesh GUNTUR DISTRICT-522237 Amaravati, Guntur , Andhra Pradesh-522237 4 KREA University 5655, Central Expressway, Sri City , Andhra Andhra Pradesh-517646 Pradesh 5 Saveetha Amaravati University 3rd Floor, Vaishnavi Complex Opp. Executive Andhra Club Vijayawada , Pradesh Andhra Pradesh-520008 6 Bharatiya Engineering Science and Gownivaripalli, Gorantla Mandal, Anantapur Andhra Technology Innovation University , Pradesh Andhra Pradesh- 7 The Global University Hollongi, Itanagar , Arunachal Arunachal Pradesh - Pradesh 8 North East Frontier Technical Sibu-Puyi, Aalo (PO) West Siang (Distt.) , Arunachal University Arunachal Pradesh -791001 Pradesh 9 Arunodaya University Lekhi Village, Naharlagun Itanagar, Distt. Arunachal Papum Pare, , Pradesh Arunachal Pradesh -791109 10 Indira Gandhi Technological and INDIRA GANDHI TECHNOLOGICAL Arunachal Medical Science University AND MEDICAL SCIENCES UNIVERSITY Pradesh ZIRO DISTRICT LOWER SUBANSIRI ARUNACHAL PRADESH 791120 Arunachal Pradesh, India , Arunachal Pradesh -

Recognition List of Examinations Recognised by the University.Pdf
MAHARSHI DAYANAND UNIVERSITY, ROHTAK ( A State University established under Haryana Act No. 25 of 1975) NAAC Accredited ‘ A’ Grade RECOGNITION/ EQUIVALENCE LIST MAY, 2014 Available from Price: � 100/- Deputy Registrar (Publications Cell) M.D. University, Rohtak (Haryana) 1 IMPORTANT NOTES 1. The eligibilit y for admission to a particular course may be determined on the basis of equivalence shown in this list and the detailed conditions given in the Admission Brochure(s)/Information Brochure/ Prospectuses etc. and the relevant Ordinances. 2. B.A./B.Sc./B.Com/B.Sc.(Home Science) pass/honours and shastri (with English) etc. courses under 10+2+3 pattern of examinations and M.A./M.Sc./M.Com/ Achar ya and LL.M. etc of two years duration after three years graduation degree or five years after +2 level ex amination of all the statutory Universities in India including open/private Universities/ deemed to be universities/ institutes of National Importance established by an Act of the state Govt./Centre govt. which are approved by the University Grants Commission (UGC) / Ministry of HRD have been recognized as equivalent to the respective course of this universit y without following the normal procedure of comparing the s yllabi and scheme of ex amination etc. List of Universities approved by UGC is appended at Appendix ‘A’. However, updated list of such universities may be seen on UGC website (www.ugc.ac.in). List of Institute of National Importance is available at Appendix ‘B’. However, updated list of such Institutes may be seen on the website (http://mhrd.gov.in) of Ministr y of HRD (Department of Higher Education Govt.