DOCSLIB.ORG

Effect of Non-Idealities – Bilinear Switched-Capacitor Filters – Filter Design Summary • Comparison of Various Filter Topologies • Data Converters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Effect of Non-Idealities – Bilinear Switched-Capacitor Filters – Filter Design Summary • Comparison of Various Filter Topologies • Data Converters EE247 Lecture 11 • Switched-Capacitor Filters (continued) – Effect of non-idealities – Bilinear switched-capacitor filters – Filter design summary • Comparison of various filter topologies • Data Converters EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 1 Summary Last Lecture • Switched-capacitor filter design considerations – DDI & LDI Integrator characteristics – Bottom-plate LDI integrator Æ overcomes parasitic sensitivity issues – Continuous-time and complex conjugate terminations – Use of T-networks to implement high capacitor ratios • Switched-capacitor filters utilizing double sampling technique • Effect of non-idealities – Opamp finite gain – Opamp finite bandwidth – Finite slew rate of the opamp (this lecture) EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 2 Switched-Capacitor Direct-Transform Discrete (DDI) Integrator C φ φ I 1 2 φ Vin φ 1 - 1 φ Cs Vo 2 + T=1/fs − Vo =−Cs × z 1 (z) − CI 1−z 1 Vin C =−s × −1 C1I z EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 3 DDI Switched-Capacitor Integrator C φ φ I 1 2 Vin φ - 1 Cs Vo + − Vo =−Cs ×z 1 = jTω (z)− , z e CI 1−z 1 Vin αα− − jT/2ω jj− =×CCss1 = ×e α =ee ωωω− since: sin CCII1−−eeejT jT/2 jT/2 2j − ω =−jeCs ×jT/2 × 1 CI 2sin()ωT/2 Cs 1 ωT/2 − jT/2ω =−ω × × e CjTI sin()ωT/2 ror se Er Ideal Integrator Magnitude Error Pha EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 4 DDI Switched-Capacitor Integrator C φ φ I 1 2 Vin φ - 1 Cs Vo + Example: Mag. & phase error for: sig 1- f max ./ fs = 1/12 Æ Mag. error = 1% or 0.1dB ω π π Phase error=- T/2= - f / fs= - /12 [radian] Æ 15 [degree] ω QintgÆ 1/( phase error @ ο in radian ) (Lecture 5 page 1) π Æ Qintg= -12/ = -3.8 2- f / fs=1/32 Æ Mag. error=0.16% or 0.014dB ω π π Phase error = T/2= - f / fs= - /32 [radian] Æ 5.6 [degree] π Qintg = -32/ = -10.2 DDI Integrator: Æ Magnitude error no problem Phase error major problem EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 5 LDI Switched-Capacitor Integrator C LDI (Lossless Discrete Integrator) Æ φ φ I 1 2 same as DDI but output is sampled ½ Vin φ clock cycle earlier - 2 LDI Cs Vo2 V − + o2 =−Cs ×z 1/2 = jTω (z)− , z e CI 1z− 1 Vin − ω =−CCse ×jT/2 = s × 1 −−+ωωω CCII1−−eeej T j T/2 j T/2 =−j Cs × 1 CI 2sin()ωT/2 Cs 1 ωT/2 =−ω × No Phase Error! CjTI sin()ωT/2 For signals at frequencies << sampling freq. Æ Magnitude error negligible Ideal Integrator Magnitude Error EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 6 Switched-Capacitor Integrator Parasitic Sensitivity C φ φ I 1 2 Vin - Vo Cp2 C Cs p3 + Cp1 Effect of parasitic capacitors: 1- Cp1 - driven by opamp o.k. 2- Cp2 - at opamp virtual gnd o.k. 3- Cp3 – Charges to Vin & discharges into CI Æ Problem parasitic sensitivity EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 7 Parasitic Insensitive Bottom-Plate Switched-Capacitor Integrator Sensitive parasitic cap. Æ Cp1 Æ rearrange circuit so that Cp1 does not charge/discharge φ 1=1 Æ Cp1 grounded φ 2=1 Æ Cp1 at virtual ground Cp2 Æ driven by a low impedance source φ φ CI 1 2 - C C s p1 Vo + Vi+ Cp2 Vi- Solution: Bottom plate capacitor integrator EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 8 Bottom Plate Switched-Capacitor Integrator φ φ φ CI 1 1 2 Vo1 - φ Cs 2 Vo + Vo2 Vi+ Vi- Output/Input z-Transform Vo1 Vo2 Note: on φ1 on φ2 − 1 Different delay from Vi+ & −1 2 Vi+ CCsszz Vi- to either output CC−−11 on φ1 II1z−− 1z Æ Special attention needed for input/output connections Vi- −1 −−CCssz12 on φ2 −− CCII1z−−11 1z EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 9 Bottom Plate Switched-Capacitor Integrator z-Transform Model φ φ CI φ 1 2 1 − −1 zz1 - 2 Vo1 −−C11φ 1z−−s 1z 2 Vo + Vo2 Vi+ −1 z12 − Input/Output−− z-transform Vi- 1z−−11 1z −1 Vi+ CCs I 2 −1 Vo1 z z 2 − −1 + 1 Vi- −CCs I 1z z 2 Vo2 LDI EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 10 LDI Switched-Capacitor Ladder Filter 1 +1 C C + s − s 2 z 2 CI CI z 1 − - + 2 − 1 z − 1 1 1 1 z 2 z 2 τ 1 sτ s 4 sτ5 −1 − −1 3 1z− 2 1z− + - + - z −1 1 − 1 − 1z − z 2 z 2 C Cs C 1 Cs − s − s + C CI CI z 2 CI I Delay around integrator loop is (z-1/2 . z+1/2 =1) Î LDI function EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 11 Effect of Opamp Nonidealities on Switched Capacitor Filter Behaviour • Opamp finite gain • Opamp finite bandwidth • Finite slew rate of the opamp • Non-linearities associated with opamp output/input characteristics EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 12 Effect of Opamp Non-Idealities Finite DC Gain φ φ CI 1 2 - Cs Vo + ≈− Cs 1 Vi+ H(s) fs DC Gain = a CI Cs 1 sf+×s Input/Output z-transform CaI Vi- −ω H(s) ≈ o s +×ω 1 o a ⇒ Qa≈ ÆFinite DC gain same effect in S.C. filters as for C.T. filters ÆIf DC gain not high enough Æ causes lowing of overall Q & droop in passband EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 13 Effect of Opamp Non-Idealities Finite Opamp Bandwidth V φ φ CI o settling 1 2 error - Cs Vo + φ Vi+ 2 Unity-gain-freq. Input/Output z-transform time Vi- = ft T=1/fs Assumption- Opamp Æ does not slew (will be revisited) Opamp has only one pole Æ exponential settling Ref: K.Martin, A. Sedra, “Effect of the OPamp Finite Gain & Bandwidth on the Performance of Switched- Capacitor Filters," IEEE Trans. Circuits Syst., vol. CAS-28, no. 8, pp. 822-829, Aug 1981. EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 14 Effect of Opamp Non-Idealities Finite Opamp Bandwidth V φ φ CI o settling 1 2 error - Cs Vo + φ Vi+ 2 Unity-gain-freq. Input/Output z-transform time Vi- = ft T=1/fs ⎡⎤−−C − ≈ 1e−+×kk eI Z 1 H(Z)H(Z)actual ideal ⎢⎥ ⎣⎦CCIs+ Cf where k =×π It × CCIss+ f fts→−−→Opamp unity gain frequency , f Clock frequency Ref: K.Martin, A. Sedra, “Effect of the OPamp Finite Gain & Bandwidth on the Performance of Switched- Capacitor Filters," IEEE Trans. Circuits Syst., vol. CAS-28, no. 8, pp. 822-829, Aug 1981. EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 15 Effect of Opamp Finite Bandwidth on Filter Magnitude Response |Τ| Τ| non-ideal /| ideal (dB) Example: For 1dB magnitude response deviation: fc /fs=1/32 Active RC 1- fc/fs=1/12 fc /fs=1/12 fc/ft~0.04 Æ ft>25fc 2- fc/fs=1/32 fc/ft~0.022 Æ ft>45fc 3- Cont.-Time fc/ft~1/700 Æ ft >700fc fc /ft EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 16 Effect of Opamp Finite Bandwidth on Filter Critical Frequency Example: Δω ω For maximum critical c / c frequency shift of <1% f /f =1/32 Active RC c s 1- fc/fs=1/32 fc/ft~0.028 fc /fs=1/12 Æ ft>36fc 2- fc/fs=1/12 fc/ft~0.046 Æ ft>22fc 3- Active RC C.T. filters fc/ft~0.008 Æ ft >125fc fc /ft Ref: K.Martin, A. Sedra, “Effect of the Opamp Finite Gain & Bandwidth on the Performance of SwitchedCapacitor Filters," IEEE Trans. Circuits Syst., vol. CAS-28, no. 8, pp. 822-829, Aug 1981. EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 17 Opamp Bandwidth Requirements for Switched- Capacitor Filters Compared to Continuous-Time Filters • Finite opamp bandwidth causes phase lag at the unity-gain frequency of the integrator for both type filters Æ Results in negative intg. Q & thus increases overall Q and gain @ results in peaking in the passband of interest • For given filter requirements, opamp bandwidth requirements much less stringent for S.C. filters compared to cont. time filters Æ lower power dissipation for S.C. filters (at low freq.s only) • Finite opamp bandwidth causes down shifting of critical frequencies in both type filters – Since cont. time filters are usually tunedÆ tuning accounts for frequency deviation – S.C. filters are untuned and thus frequency shift could cause problems specially for narrow-band filters EECS 247 Lecture 11: S.C. Filters/ Data Converters © 2006 H. K. Page 18 Sources of Distortion in Switched- Capacitor Filters • Distortion induced by finite slew rate of the opamp • Opamp output/input transfer function non- linearity- similar to cont. time filters • Distortion incurred by finite setting time of the opamp • Capacitor non-linearity- similar to cont. time filters • Distortion due to switch clock feed-through and charge injection EECS 247 Lecture 11: S.C.
Load more

Recommended publications
  • Virtual Analog (VA) Filter Implementation and Comparisons Copyright © 2013 Will Pirkle
    App Note 4"Virtual Analog (VA) Filter Implementation and Comparisons "Copyright © 2013 Will Pirkle Virtual Analog (VA) Filter Implementation and Comparisons Will Pirkle I have had several requests from readers to do a Virtual Analog (VA) Filter Implementation plug-in. The source of these designs is a book electronically published in June 2012 named The Art of VA Filter Design by Vadim Zavalishin. This awesome piece of work is free and available from many sources including my own site www.willpirkle.com. This short book is an excellent introduction to basic analog filtering theory as well as digital transformations. It is so concise in this respect that I am considering using it as part of the text materials for an Advanced Analog Circuits class I teach. I highly recommend this excellent book - you will need to understand its content to use this App Note; for the most part I use the same variable names as the book so you will want to use it as a reference. Zavalishinʼs derivations and descriptions are so well thought out and so well written that it makes no sense for me to repeat them here and I donʼt think it can be simplified any more that it already is in his book. Another reason that I enjoyed this book is that the author followed a similar derivation to reach the bilinear transform as my DSP professor (Claude Lindquist) did when I was in graduate school; in fact I use part of that same derivation in my classes and book. Also similar was the use of an integrator as a prototype filter to generate the discrete time transforms.
    [Show full text]
  • ECGR4124 Digital Signal Processing Exam 2 Spring 2017 Name
    ECGR4124 Digital Signal Processing Exam 2 Spring 2017 Name: _____________________________________ LAST 4 NUMBERS of Student Number: _____ Do NOT begin until told to do so Make sure that you have all pages before starting NO TEXTBOOK, NO CALCULATOR, NO CELL PHONES/WIRELESS DEVICES Open handouts, 2 sheet front/back notes, NO problem handouts, NO exams, NO quizzes DO ALL WORK IN THE SPACE GIVEN Do NOT use the back of the pages, do NOT turn in extra sheets of work/paper Multiple-choice answers should be within 5% of correct value Show ALL work, even for multiple choice ACADEMIC INTEGRITY: Students have the responsibility to know and observe the requirements of The UNCC Code of Student Academic Integrity. This code forbids cheating, fabrication or falsification of information, multiple submission of academic work, plagiarism, abuse of academic materials, and complicity in academic dishonesty. Unless otherwise noted: F{} denotes Discrete time Fourier transform {DTFT, DFT, or Continuous, as implied in problem} F-1{} denotes inverse Fourier transform ω denotes frequency in rad/sample, Ω denotes frequency in rad/second ∗ denotes linear convolution, N denotes circular convolution x*(t) denotes the conjugate of x(t) Useful constants, etc: e ≈ 2.72 π ≈ 3.14 e2 ≈ 7.39 e4 ≈ 54.6 e-0.5 ≈ 0.607 e-0.25 ≈ 0.779 1/e ≈ 0.37 √2 ≈ 1.41 e-2 ≈ 0.135 √3 ≈ 1.73 e-4 ≈ 0.0183 √5 ≈ 2.22 √7 ≈ 2.64 √10 ≈ 3.16 ln( 2 ) ≈ 0.69 ln( 4 ) ≈ 1.38 log10( 2 ) ≈ 0.30 log10( 3 ) ≈ 0.48 log10( 10 ) ≈ 1.0 log10( 0.1 ) ≈ -1 1/π ≈ 0.318 sin(0.1) ≈ 0.1 tan(1/9) ≈ 1/9 cos(π / 4) ≈ 0.71 cos( A ) cos ( B ) = 0.5 cos(A - B) + 0.5 cos(A + B) ejθ = cos(θ) + j sin(θ) 1/10 5 Points Each, Circle the Best Answer 1.
    [Show full text]
  • Digital Signal Processing I Exam 2 Fall 1999 Session 17 Live: 21 Oct
    Digital Signal Processing I Exam 2 Fall 1999 Session 17 Live: 21 Oct. 1999 Cover Sheet Test Duration: 75 minutes. Open Book but Closed Notes. Calculators NOT allowed. This test contains four problems. All work should be done in the blue books provided. Do not return this test sheet, just return the blue books. Prob. No. Topic of Problem Points 1. Digital Upsampling 35 2. Digital Subbanding 25 3. Multi-Stage Upsampling/Interpolation 20 4. IIR Filter Design Via Bilinear Transform 20 1 Digital Signal Processing I Exam 2 Fall 1999 Session 17 Live: 21 Oct. 1999 Problem 1. [35 points] X (F) H (ω) a LP 1/4W 2 F ω W W π 3π π π 3π π 4 4 4 4 x (t) h [n] a Ideal A/D x [n] w [n] Lowpass Filter y [n] 2 π LP 3π F = 4W ω = ω = s p 4 s 4 gain =2 Figure 1. The analog signal xa(t) with CTFT Xa(F ) shown above is input to the system above, where x[n]=xa(n/Fs)withFs =4W ,and sin( π n) cos( π n) h [n]= 2 4 , −∞ <n<∞, LP π n − n2 2 1 4 | |≤ π 3π ≤| |≤ such that HLP (ω)=2for ω 4 , HLP (ω)=0for 4 ω π,andHLP (ω) has a cosine π 3π roll-off from 1 at ωp = 4 to 0 at ωs = 4 . Finally, the zero inserts may be mathematically described as ( x( n ),neven w[n]= 2 0,nodd (a) Plot the magnitude of the DTFT of the output y[n], Y (ω), over −π<ω<π.
    [Show full text]
  • IIR Filters (II)
    Lecture 8 - IIR Filters (II) James Barnes ([email protected]) Spring 2009 Colorado State University Dept of Electrical and Computer Engineering ECE423 – 1 / 27 Lecture 8 Outline ● Introduction ● Digital Filter Design by Analog → Digital Conversion ● (Probably next lecture) ”All Digital” Design Algorithms ● (Next lecture) Conversion of Filter Types by Frequency Transformation Colorado State University Dept of Electrical and Computer Engineering ECE423 – 2 / 27 ❖ Lecture 8 Outline Introduction ❖ IIR Filter Design Overview Method: Impulse Invariance for IIR FIlters Approximation of Derivatives Bilinear Transform Matched Z-Transform Introduction Colorado State University Dept of Electrical and Computer Engineering ECE423 – 3 / 27 IIR Filter Design Overview ● Methods which start from analog design ✦ Impulse Invariance ✦ Approximation of Derivatives ✦ Bilinear Transform ✦ Matched Z-transform All are different methods of mapping the s-plane onto the z-plane ● Methods which are ”all digital” ✦ Least-squares ✦ McClellan-Parks Colorado State University Dept of Electrical and Computer Engineering ECE423 – 4 / 27 ❖ Lecture 8 Outline Introduction Method: Impulse Invariance for IIR FIlters ❖ Impulse Invariance ❖ Impulse Invariance (2) ❖ Impulse Invariance (3) ❖ Impulse Invariance (5) ❖ Impulse Invariance Procedure ❖ Impulse Invariance Example Method: Impulse Invariance for IIR FIlters ❖ Impulse Invariance Example (2) Approximation of Derivatives Bilinear Transform Matched Z-Transform Colorado State University Dept of Electrical and Computer Engineering ECE423 – 5 / 27 Impulse Invariance We start by sampling the impulse response of the analog filter: ha(t) h[n]= ha(nt0) t0 Sampling Theorem gives relation between Fourier Transform of sampled and continuous ”signals”: ∞ 1 ω 2πk H(z)|z=ejω = Ha(j − j ), (1) t0 t0 t0 k=X−∞ where ω =Ωt0 = 2πf/fs and f is the analog frequency in Hz.
    [Show full text]
  • Signal Approximation Using the Bilinear Transform
    SIGNAL APPROXIMATION USING THE BILINEAR TRANSFORM Archana Venkataraman, Alan V. Oppenheim MIT Digital Signal Processing Group 77 Massachusetts Avenue, Cambridge, MA 02139 [email protected], [email protected] ABSTRACT The analysis presented in this paper has application in contexts This paper explores the approximation properties of a unique basis where only a fixed number of DT values can be used to represent a expansion, which realizes a bilinear frequency warping between a CT signal. For example, in a binary detection problem, one might continuous-time signal and its discrete-time representation. We in- want to limit the number of digital multiplies used to compute the vestigate the role that certain parameters and signal characteristics inner product of two CT signals. Numerical simulations of this sce- have on these approximations, and we extend the analysis to a win- nario suggest that the bilinear expansion achieves a better detection dowed representation, which increases the overall time resolution. performance than Nyquist sampling for certain signal classes. Approximations derived from the bilinear representation and from Nyquist sampling are compared in the context of a binary detection 2. THE BILINEAR REPRESENTATION problem. Simulation results indicate that, for many types of signals, the bilinear approximations achieve a better detection performance. As derived in [1], the network shown in Fig. 1 realizes a one-to-one Index Terms— Signal Representations, Approximation Meth- frequency warping between the Laplace and Z-transform domains ods, Bilinear Transformations, Signal Detection according to the bilinear transform. Specifically, the Laplace trans- form F (s) of the signal f(t) and the Z-transform F (z) of the se- f[n] 1.
    [Show full text]
  • Visual and Intuitive Approach to Explaining Digitized Controllers
    Paper ID #16436 Visual and Intuitive Approach to Explaining Digitized Controllers Dr. Daniel Raviv, Florida Atlantic University Dr. Raviv is a Professor of Computer & Electrical Engineering and Computer Science at Florida Atlantic University. In December 2009 he was named Assistant Provost for Innovation and Entrepreneurship. With more than 25 years of combined experience in the high-tech industry, government and academia Dr. Raviv developed fundamentally different approaches to ”out-of-the-box” thinking and a breakthrough methodology known as ”Eight Keys to Innovation.” He has been sharing his contributions with profession- als in businesses, academia and institutes nationally and internationally. Most recently he was a visiting professor at the University of Maryland (at Mtech, Maryland Technology Enterprise Institute) and at Johns Hopkins University (at the Center for Leadership Education) where he researched and delivered processes for creative & innovative problem solving. For his unique contributions he received the prestigious Distinguished Teacher of the Year Award, the Faculty Talon Award, the University Researcher of the Year AEA Abacus Award, and the President’s Leadership Award. Dr. Raviv has published in the areas of vision-based driverless cars, green innovation, and innovative thinking. He is a co-holder of a Guinness World Record. His new book is titled: ”Everyone Loves Speed Bumps, Don’t You? A Guide to Innovative Thinking.” Dr. Daniel Raviv received his Ph.D. degree from Case Western Reserve University in 1987 and M.Sc. and B.Sc. degrees from the Technion, Israel Institute of Technology in 1982 and 1980, respectively. Paul Benedict Caballo Reyes, Florida Atlantic University Paul Benedict Reyes is an Electrical Engineering major in Florida Atlantic University who expects to graduate Spring 2016.
    [Show full text]
  • The Z-Transform
    CHAPTER 33 The z-Transform Just as analog filters are designed using the Laplace transform, recursive digital filters are developed with a parallel technique called the z-transform. The overall strategy of these two transforms is the same: probe the impulse response with sinusoids and exponentials to find the system's poles and zeros. The Laplace transform deals with differential equations, the s-domain, and the s-plane. Correspondingly, the z-transform deals with difference equations, the z-domain, and the z-plane. However, the two techniques are not a mirror image of each other; the s-plane is arranged in a rectangular coordinate system, while the z-plane uses a polar format. Recursive digital filters are often designed by starting with one of the classic analog filters, such as the Butterworth, Chebyshev, or elliptic. A series of mathematical conversions are then used to obtain the desired digital filter. The z-transform provides the framework for this mathematics. The Chebyshev filter design program presented in Chapter 20 uses this approach, and is discussed in detail in this chapter. The Nature of the z-Domain To reinforce that the Laplace and z-transforms are parallel techniques, we will start with the Laplace transform and show how it can be changed into the z- transform. From the last chapter, the Laplace transform is defined by the relationship between the time domain and s-domain signals: 4 X(s) ' x(t) e &st dt m t '&4 where x(t) and X(s) are the time domain and s-domain representation of the signal, respectively.
    [Show full text]
  • IIR Filters (II)
    Lecture 8 - IIR Filters (II) James Barnes ([email protected]) Spring 2014 Colorado State University Dept of Electrical and Computer Engineering ECE423 – 1 / 29 Lecture 8 Outline ● Introduction ● Digital Filter Design by Analog → Digital Conversion ● (Probably next lecture) ”All Digital” Design Algorithms ● (Next lecture) Conversion of Filter Types by Frequency Transformation Colorado State University Dept of Electrical and Computer Engineering ECE423 – 2 / 29 ❖ Lecture 8 Outline Introduction ❖ IIR Filter Design Overview Method: Impulse Invariance for IIR FIlters Approximation of Derivatives Bilinear Transform Matched Z-Transform Introduction Colorado State University Dept of Electrical and Computer Engineering ECE423 – 3 / 29 IIR Filter Design Overview ● Methods which start from analog design ✦ Impulse Invariance ✦ Approximation of Derivatives ✦ Bilinear Transform ✦ Matched Z-transform All are different methods of mapping the s-plane onto the z-plane ● Methods which are ”all digital” ✦ Least-squares ✦ McClellan-Parks Colorado State University Dept of Electrical and Computer Engineering ECE423 – 4 / 29 ❖ Lecture 8 Outline Introduction Method: Impulse Invariance for IIR FIlters ❖ Impulse Invariance ❖ Impulse Invariance (2) ❖ Impulse Invariance (3) ❖ Impulse Invariance (4) ❖ Impulse Invariance Procedure ❖ Impulse Invariance Example Method: Impulse Invariance for IIR FIlters ❖ Impulse Invariance Example (2) Approximation of Derivatives Bilinear Transform Matched Z-Transform Colorado State University Dept of Electrical and Computer Engineering ECE423 – 5 / 29 Impulse Invariance We start by sampling the impulse response of the analog filter: ha(t) h[n]= ha(nt0) t0 Sampling Theorem gives relation between Fourier Transform of sampled and continuous ”signals”: ∞ 1 ω 2πk H(z)|z=ejω = Ha(j − j ), (1) t0 t0 t0 k=X−∞ where ω =Ωt0 = 2πf/fs and f is the analog frequency in Hz.
    [Show full text]
  • Al-Alaoui Operator and the New Transformation Polynomials for Discretization of Analogue Systems
    Electr Eng (2008) 90:455–467 DOI 10.1007/s00202-007-0092-0 ORIGINAL PAPER Al-Alaoui operator and the new transformation polynomials for discretization of analogue systems Mohamad Adnan Al-Alaoui Received: 22 August 2007 / Accepted: 1 December 2007 / Published online: 8 January 2008 © Springer-Verlag 2007 Abstract The “new transformation polynomials for discret- The bilinear transform meets the above requirements. ization of analogue systems” was recently introduced. The However, it introduces a warping effect due to its nonlinear- work proposes that the discretization of 1/sn should be done ity, albeit it can be ameliorated somewhat by a pre-warping independently rather than by raising the discrete representa- technique. tion of 1/s to the power n. Several examples are given in to The backward difference transform satisfies the first con- back this idea. In this paper it is shown that the “new transfor- dition, but the second condition is not completely satisfied, mation polynomials for discretization of analogue systems” since the imaginary axis of the s-plane maps onto the cir- is exactly the same as the parameterized Al-Alaoui opera- cumference in the z-plane centered at z = 1/2 and having a tor. In the following sections, we will show that the same radius of 1/2. The mapping meets condition 2 rather closely results could be obtained with the parameterized Al-Alaoui for low frequencies [1–6]. operator. Other transforms were introduced in attempts to obtain better approximations [7–11]. In particular, in [7,8]the Keywords Al-Alaoui operator · Digital filters · approach interpolates the rectangular integration rules and Discretization · s-to-z transforms the trapezoidal integration rule.
    [Show full text]
  • Digital Signal Processing
    Chapter 5. Digital Signal Processing Digital Signal Processing Academic and Research Staff Professor Alan V. Oppenheim, Professor Arthur B. Baggeroer, Dr. Charles E. Rohrs. Visiting Scientists and Research Affiliates Dr. Dan E. Dudgeon1, Dr. Yonina Eldar2, Dr. Ehud Weinstein3, Dr. Maya R. Said4 Graduate Students Thomas Baran, Sourav Dey, Zahi Karam, Alaa Kharbouch, Jon Paul Kitchens, Melanie Rudoy, Joseph Sikora III, Archana Venkataraman, Dennis Wei, Matthew Willsey. UROP Student Jingdong Chen Technical and Support Staff Eric Strattman Introduction The Digital Signal Processing Group develops signal processing algorithms that span a wide variety of application areas including speech and image processing, sensor networks, communications, radar and sonar. Our primary focus is on algorithm development in general, with the applications serving as motivating contexts. Our approach to new algorithms includes some unconventional directions, such as algorithms based on fractal signals, chaotic behavior in nonlinear dynamical systems, quantum mechanics and biology in addition to the more conventional areas of signal modeling, quantization, parameter estimation, sampling and signal representation. When developing new algorithms, we often look to nature for inspiration and as a metaphor for new signal processing directions. Falling into this category to a certain extent, is our previous work on fractals, chaos, and solitons. 1 BAE Systems IEWS, Senior Principal Systems Engineer, Nashua, New Hampshire. 2 Department of Electrical Engineering, Faculty of Engineering, Technion-Israel Institute of Technology, Israel. 3 Department of Electrical Engineering, Systems Division, Faculty of Engineering, Tel-Aviv University, Israel; adjunct scientist, Department of Applied Ocean Physics and Engineering, Woods Hole Oceanographic Institution, Woods Hole, Massachusetts. 4 Visiting Scientist, Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, Massachusetts.
    [Show full text]
  • Design of IIR Filters.Pdf
    Design of IIR Filters Elena Punskaya www-sigproc.eng.cam.ac.uk/~op205 Some material adapted from courses by Prof. Simon Godsill, Dr. Arnaud Doucet, Dr. Malcolm Macleod and Prof. Peter Rayner 1 IIR vs FIR Filters 2 IIR as a class of LTI Filters Difference equation: Transfer function: To give an Infinite Impulse Response (IIR), a filter must be recursive, that is, incorporate feedback N ≠ 0, M ≠ 0 the recursive (previous output) terms feed back energy into the filter input and keep it going. (Although recursive filters are not necessarily IIR) 3 IIR Filters Design from an Analogue Prototype • Given filter specifications, direct determination of filter coefficients is too complex • Well-developed design methods exist for analogue low-pass filters • Almost all methods rely on converting an analogue filter to a digital one 4 Analogue filter Rational Transfer Function () 5 Analogue to Digital Conversion Im (z) Re (z) 6 Impulse Invariant method 7 Impulse Invariant method: Steps 1. Compute the Inverse Laplace transform to get impulse response of the analogue filter 2. Sample the impulse response (quickly enough to avoid aliasing problem) 3. Compute z-transform of resulting sequence 8 Example 1 – Impulse Invariant Method Consider first order analogue filter = 1 - Corresponding impulse response is δ - v The presence of delta term prevents sampling of impulse response which thus cannot be defined Fundamental problem: high-pass and band-stop filters have functions with numerator and denominator polynomials of the same degree and thus cannot be designed using this method 9 Example 2 – Impulse Invariant Method Consider an analogue filter Step 1.
    [Show full text]
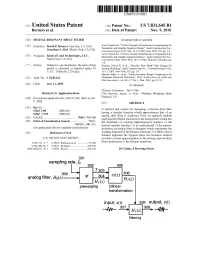
  • (73) Assignee: Kind of Loud Technologies, LLC, E.R.E
    US007831645B1 (12) United States Patent (10) Patent No.: US 7,831,645 B1 Berners et al. (45) Date of Patent: Nov. 9, 2010 (54) DIGITAL RESONANT SHELF FILTER OTHER PUBLICATIONS (75)75 Inventors: E.id P. s "E. S. R. SEGs) Azizi.Parametric Seyed-Ali. and Graphic “A New Equalizer Concept Banks'.of Interference Audio CompensationEngineering Soc., for Onanan S. ADel, Menlo Park, Convention Paper 5482, Sep. 21-24, 2001, New York, NY. pp. 1-8. (73) Assignee: Kind of Loud Technologies, LLC, Azizi,E.R.E. Seyed-Ali, “A New C t of Interf C tion f Santa Cruz, CA (US) Convention Paper 5629, May 10-13, 2002, Munich, Germany, pp. 1-8. (*) Notice: Subject to any disclaimer, the term of this Berners, David P. et al., “Discrete-Time Shelf Filter Design for patent is extended or adjusted under 35 Analog Modeling”. Audio Engineering Soc., Convention Paper, Oct. U.S.C. 154(b) by 1274 days. 11-13, 2003, New York, NY. pp. 1-5. Blesser, Barry A., et al., “Audio Dynamic Range Compression for (21) Appl. No.: 11/249,162 Minimum Perceived Distortion', IEEE Transactions on Audio and Electroacoustics, vol. AU-17, No. 1, Mar. 1969, pp. 22-32. (22) Filed: Oct. 11, 2005 (Continued) Primary Examiner Tan V Mai Related U.S. Application Data (74) Attorney, Agent, or Firm Pillsbury Winthrop Shaw (60) Provisional application No. 60/617,343, filed on Oct. Pittman LLP 8, 2004. s (57) ABSTRACT (51) Int. Cl. A method and system for designing a discrete-time filter G06 L/00 (2006.01) having a transfer function which approximates that of an G06F 7/10 (2006.01) - 0 52) U.S.
    [Show full text]