Wind Driven Capillary-Gravity Waves on Titan's Lakes: Hard to Detect Or
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Saturn Satellites As Seen by Cassini Mission
Saturn satellites as seen by Cassini Mission A. Coradini (1), F. Capaccioni (2), P. Cerroni(2), G. Filacchione(2), G. Magni,(2) R. Orosei(1), F. Tosi(1) and D. Turrini (1) (1)IFSI- Istituto di Fisica dello Spazio Interplanetario INAF Via fosso del Cavaliere 100- 00133 Roma (2)IASF- Istituto di Astrofisica Spaziale e Fisica Cosmica INAF Via fosso del Cavaliere 100- 00133 Roma Paper to be included in the special issue for Elba workshop Table of content SATURN SATELLITES AS SEEN BY CASSINI MISSION ....................................................................... 1 TABLE OF CONTENT .................................................................................................................................. 2 Abstract ....................................................................................................................................................................... 3 Introduction ................................................................................................................................................................ 3 The Cassini Mission payload and data ......................................................................................................................... 4 Satellites origin and bulk characteristics ...................................................................................................................... 6 Phoebe ............................................................................................................................................................................... -

The Lakes and Seas of Titan • Explore Related Articles • Search Keywords Alexander G
EA44CH04-Hayes ARI 17 May 2016 14:59 ANNUAL REVIEWS Further Click here to view this article's online features: • Download figures as PPT slides • Navigate linked references • Download citations The Lakes and Seas of Titan • Explore related articles • Search keywords Alexander G. Hayes Department of Astronomy and Cornell Center for Astrophysics and Planetary Science, Cornell University, Ithaca, New York 14853; email: [email protected] Annu. Rev. Earth Planet. Sci. 2016. 44:57–83 Keywords First published online as a Review in Advance on Cassini, Saturn, icy satellites, hydrology, hydrocarbons, climate April 27, 2016 The Annual Review of Earth and Planetary Sciences is Abstract online at earth.annualreviews.org Analogous to Earth’s water cycle, Titan’s methane-based hydrologic cycle This article’s doi: supports standing bodies of liquid and drives processes that result in common 10.1146/annurev-earth-060115-012247 Annu. Rev. Earth Planet. Sci. 2016.44:57-83. Downloaded from annualreviews.org morphologic features including dunes, channels, lakes, and seas. Like lakes Access provided by University of Chicago Libraries on 03/07/17. For personal use only. Copyright c 2016 by Annual Reviews. on Earth and early Mars, Titan’s lakes and seas preserve a record of its All rights reserved climate and surface evolution. Unlike on Earth, the volume of liquid exposed on Titan’s surface is only a small fraction of the atmospheric reservoir. The volume and bulk composition of the seas can constrain the age and nature of atmospheric methane, as well as its interaction with surface reservoirs. Similarly, the morphology of lacustrine basins chronicles the history of the polar landscape over multiple temporal and spatial scales. -

The Exploration of Titan with an Orbiter and a Lake Probe
Planetary and Space Science ∎ (∎∎∎∎) ∎∎∎–∎∎∎ Contents lists available at ScienceDirect Planetary and Space Science journal homepage: www.elsevier.com/locate/pss The exploration of Titan with an orbiter and a lake probe Giuseppe Mitri a,n, Athena Coustenis b, Gilbert Fanchini c, Alex G. Hayes d, Luciano Iess e, Krishan Khurana f, Jean-Pierre Lebreton g, Rosaly M. Lopes h, Ralph D. Lorenz i, Rachele Meriggiola e, Maria Luisa Moriconi j, Roberto Orosei k, Christophe Sotin h, Ellen Stofan l, Gabriel Tobie a,m, Tetsuya Tokano n, Federico Tosi o a Université de Nantes, LPGNantes, UMR 6112, 2 rue de la Houssinière, F-44322 Nantes, France b Laboratoire d’Etudes Spatiales et d’Instrumentation en Astrophysique (LESIA), Observatoire de Paris, CNRS, UPMC University Paris 06, University Paris-Diderot, Meudon, France c Smart Structures Solutions S.r.l., Rome, Italy d Center for Radiophysics and Space Research, Cornell University, Ithaca, NY 14853, United States e Dipartimento di Ingegneria Meccanica e Aerospaziale, Università La Sapienza, 00184 Rome, Italy f Institute of Geophysics and Planetary Physics, Department of Earth and Space Sciences, Los Angeles, CA, United States g LPC2E-CNRS & LESIA-Obs., Paris, France h Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, United States i Johns Hopkins University, Applied Physics Laboratory, Laurel, MD, United States j Istituto di Scienze dell‘Atmosfera e del Clima (ISAC), Consiglio Nazionale delle Ricerche (CNR), Rome, Italy k Istituto di Radioastronomia (IRA), Istituto Nazionale -

Wave Constraints for Titan’S Jingpo Lacus and Kraken Mare
Icarus 211 (2011) 722–731 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Wave constraints for Titan’s Jingpo Lacus and Kraken Mare from VIMS specular reflection lightcurves ⇑ Jason W. Barnes a, , Jason M. Soderblom b, Robert H. Brown b, Laurence A. Soderblom c, Katrin Stephan d, Ralf Jaumann d, Stéphane Le Mouélic e, Sebastien Rodriguez f, Christophe Sotin g, Bonnie J. Buratti g, Kevin H. Baines g, Roger N. Clark h, Philip D. Nicholson i a Department of Physics, University of Idaho, Moscow, ID 83844-0903, United States b Department of Planetary Sciences, University of Arizona, Tucson, AZ 85721, United States c United States Geological Survey, Flagstaff, AZ 86001, United States d DLR, Institute of Planetary Research, Rutherfordstrasse 2, D-12489 Berlin, Germany e Laboratoire de Planétologie et Géodynamique, CNRS UMR6112, Université de Nantes, France f Laboratoire AIM, Centre d’ètude de Saclay, DAPNIA/Sap, Centre de l’Orme des M erisiers, bât. 709, 91191 Gif/Yvette Cedex, France g Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, United States h United States Geological Survey, Denver, CO 80225, United States i Department of Astronomy, Cornell University, Ithaca, NY 14853, United States article info abstract Article history: Stephan et al. (Stephan, K. et al. [2010]. Geophys. Res. Lett. 37, 7104–+.) first saw the glint of sunlight Received 15 April 2010 specularly reflected off of Titan’s lakes. We develop a quantitative model for analyzing the photometric Revised 18 September 2010 lightcurve generated during a flyby in which the specularly reflected light flux depends on the fraction of Accepted 28 September 2010 the solar specular footprint that is covered by liquid. -

Formation Et Développement Des Lacs De Titan : Interprétation Géomorphologique D’Ontario Lacus Et Analogues Terrestres Thomas Cornet
Formation et Développement des Lacs de Titan : Interprétation Géomorphologique d’Ontario Lacus et Analogues Terrestres Thomas Cornet To cite this version: Thomas Cornet. Formation et Développement des Lacs de Titan : Interprétation Géomorphologique d’Ontario Lacus et Analogues Terrestres. Planétologie. Ecole Centrale de Nantes (ECN), 2012. Français. NNT : 498 - 254. tel-00807255v2 HAL Id: tel-00807255 https://tel.archives-ouvertes.fr/tel-00807255v2 Submitted on 28 Nov 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Ecole Centrale de Nantes ÉCOLE DOCTORALE SCIENCES POUR L’INGENIEUR, GEOSCIENCES, ARCHITECTURE Année 2012 N° B.U. : Thèse de DOCTORAT Spécialité : ASTRONOMIE - ASTROPHYSIQUE Présentée et soutenue publiquement par : THOMAS CORNET le mardi 11 Décembre 2012 à l’Université de Nantes, UFR Sciences et Techniques TITRE FORMATION ET DEVELOPPEMENT DES LACS DE TITAN : INTERPRETATION GEOMORPHOLOGIQUE D’ONTARIO LACUS ET ANALOGUES TERRESTRES JURY Président : M. MANGOLD Nicolas Directeur de Recherche CNRS au LPGNantes Rapporteurs : M. COSTARD François Directeur de Recherche CNRS à l’IDES M. DELACOURT Christophe Professeur des Universités à l’Université de Bretagne Occidentale Examinateurs : M. BOURGEOIS Olivier Maître de Conférences HDR à l’Université de Nantes M. GUILLOCHEAU François Professeur des Universités à l’Université de Rennes I M. -

Titan Mare Explorer
TiME Titan Mare Explorer Titan Mare Explorer (TiME): Proxemy Research First Exploration of an Extraterrestrial Sea Ellen Stofan TiME Science . Discovery of lakes and seas in Titan’s northern hemisphere confirmed the expectation that liquid hydrocarbons exist . Detection of the presence of ethane in Ontario Lacus near the South Pole (Brown et al., 2008) . 2 distinct types of features- lakes and seas, likely 10’s, >100 m deep . Post-Cassini, major questions will remain on the chemistry of sea liquids, their role in the overall methane cycle, the origin of sea basins, and seasonal processes and variability TiME Proprietary Information/Competition Sensitive Titan’s methane cycle • Titan’s methane cycle is analogous to Earth’s hydrologic cycle, with meteorological working fluid existing in condensed phase on surface and within crust, cycling through the surface atmosphere system and transporting mass and energy TiME Proprietary Information/Competition Sensitive TiME Science Target •Target: Ligeia Mare (78°N, 250°W) –One of the largest seas identified to date on Titan, surface area ~100,000 km2 –Backup target- Kraken Mare TiME Proprietary Information/Competition Sensitive TiME Science Team .PI: Ellen Stofan (Proxemy Research) .Co-Is: .Jonathan Lunine (Univ. of Az.) - Deputy PI .Ralph Lorenz (APL)- Project Scientist .Oded Aharonson (CalTech) .Beau Bierhaus (LM) .Ben Clark (SSI) .Caitlin Griffith (Univ. Arizona) .Ari-Matti Harri (FMI) .Erich Karkoschka (Univ. Arizona) .Randy Kirk (USGS) .Paul Mahaffy (Goddard) .Claire Newman (Ashima Research) .Mike Ravine (MSSS) .Melissa Trainer (GSFC) .Elizabeth Turtle (APL) .Hunter Waite (SWRI) .Margaret Yelland (Univ. Southampton) .John Zarnecki (Open University) TiME Proprietary Information/Competition Sensitive TiME Science Goals and Objectives . -
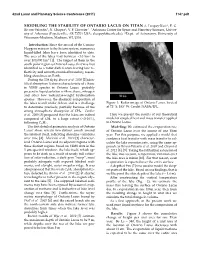
Modeling the Stability of Ontario Lacus on Titan A
42nd Lunar and Planetary Science Conference (2011) 1747.pdf MODELING THE STABILITY OF ONTARIO LACUS ON TITAN A. Luspay-Kuti1, E. G. Rivera-Valentin1, N. Chopra2, V. F. Chevrier1. 1Arkansas Center for Space and Planetary Sciences, Univer- sity of Arkansas (Fayetteville, AR 72701 USA; [email protected]); 2Dept. of Astronomy, University of Wisconsin-Madison, Madison, WI, USA Introduction: Since the arrival of the Cassini- Huygens mission to the Saturn system, numerous liquid-filled lakes have been identified to date. The area of the lakes vary between <10 km2 to over 100,000 km2 [1]. The largest of them in the south polar region is Ontario Lacus, that was first identified as a radar dark feature having low re- flectivity and smooth, rounded boundary, resem- bling shorelines on Earth. During the T38 flyby, Brown et al. 2008 [2] iden- tified absorption features characteristic of ethane in VIMS spectra in Ontario Lacus, probably present in liquid solution with methane, nitrogen and other low molecular-weight hydrocarbon species. However, the chemical composition of the lakes is still under debate and is a challenge Figure 1: Radar image of Ontario Lacus, located ◦ ◦ to determine precisely, partially because of the at 72 S, 183 W. Credit: NASA/JPL. strong atmospheric absorption of CH4. Cordier et al. 2009 [3] proposed that the lakes are indeed Here we present the results of our theoretical composed of CH4 to a large extent (∼5-10%), model of coupled heat and mass transfer applied following C2H6. to Ontario Lacus. The first detailed geometric analysis of Ontario Modeling: We estimated the evaporation rate Lacus’ shore reveals two distinct annuli around of Ontario Lacus over the course of one Titan the lakebed itself, indicating shoreline variations year. -

Active Shoreline of Ontario Lacus, Titan: a Morphological Study of the Lake and Its Surroundings S
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Caltech Authors - Main GEOPHYSICAL RESEARCH LETTERS, VOL. 37, L05202, doi:10.1029/2009GL041821, 2010 Click Here for Full Article Active shoreline of Ontario Lacus, Titan: A morphological study of the lake and its surroundings S. Wall,1 A. Hayes,2 C. Bristow,3 R. Lorenz,4 E. Stofan,5,6 J. Lunine,7 A. Le Gall,1 M. Janssen,1 R. Lopes,1 L. Wye,8 L. Soderblom,9 P. Paillou,10 O. Aharonson,2 H. Zebker,8 T. Farr,1 G. Mitri,2 R. Kirk,9 K. Mitchell,1 C. Notarnicola,11 D. Casarano,12 and B. Ventura13 Received 19 November 2009; revised 6 January 2010; accepted 14 January 2010; published 6 March 2010. [1] Of more than 400 filled lakes now identified on Titan, has been described [Tokano et al., 2006; Hueso and the first and largest reported in the southern latitudes is Sánchez‐Lavega, 2006]. Large‐scale oceans do not exist Ontario Lacus, which is dark in both infrared and [e.g., West et al., 2005; Elachi et al., 2005, 2006], but what microwave. Here we describe recent observations including appear to be liquid‐filled basins have been imaged, ranging synthetic aperture radar (SAR) images by Cassini’s radar in size from <10 to more than 105 km2 [Stofan et al., 2007; instrument (l = 2 cm) and show morphological evidence Hayes et al., 2008]. Ontario Lacus, a 200 km × 70 km lake for active material transport and erosion. Ontario Lacus at 74S, 180W, was first observed in near‐infrared [Turtle et lies in a shallow depression, with greater relief on the al., 2009]. -

Titan's Atmospheric and Surface Properties of the Ontario Lacus
Geophysical Research Abstracts, Vol. 11, EGU2009-12695, 2009 EGU General Assembly 2009 © Author(s) 2009 Titan’s atmospheric and surface properties of the Ontario Lacus region from Cassini/VIMS remote sensing A. Negrão (1,2), A. Adriani (1), M. Moriconi (1), A. Coradini (1), E. D’Aversa (1), G. Filacchione (1), and J. Lunine (3) (1) Istituto di Fisica dello Spazio Interplanetario, Roma, Italia ([email protected]), (2) Escola Superior de Tecnologia e Gestão do Instituto Politécnico de Leiria, Leiria, Portugal, (3) Lunar and Planetary Lab, University of Arizona, Tucson, USA The existence of oceans or lakes of liquid hydrocarbons on Titan’s surface was predicted more than 20 years ago. These would serve as a source of atmospheric methane and would also contain the end products of the photochemical reactions occurring high in the atmosphere. Although no oceans were ever found, lake-like features poleward of 70°N were first detected by the radar instrument onboard Cassini on July 2006. Before that, Cassini Imaging Science Subsystem (ISS) images of the south pole from June 2005 revealed an intriguing lake-like dark feature named Ontario Lacus. Recently an interesting and important result has been published about the identification of liquid ethane contained within Ontario Lacus (Brown et al. 2008). The authors analysed a near-infrared Visual and Infrared Mapping Spectrometer (VIMS) observation of the Ontario Lacus performed the 2007 December 4, during the T38 flyby. Their result needs nevertheless to be confirmed and improved using a more detailed methodology. Here we report on the analysis of this observation using a radiative transfer model (the libRadtran pack- age) to simulate the atmospheric contribution. -

Payload Concept Proposal A.T.L.A.S
PAYLOAD CONCEPT PROPOSAL A.T.L.A.S. Scottsboro Team 2 “Dropping our world, Picking up another” Payload Concept Proposal Titan Environmental and Atmospheric Measurement Mission 1.0 Introduction As recommended by NASA’s 2006 Solar System Exploration (SSE) Roadmap, the Titan Saturn System Mission (TSSM) has planned a mission to study the diverse and dynamic conditions in the ionosphere where complex organic chemistry begins, observe seasonal changes in the atmosphere, and make global near-infrared and radar altimetric maps of the surface. The TSSM was adopted by InSPIRESS under the name of the Titan Environmental and Atmospheric Measurement (TEAM) mission. In accompaniment to the TEAM mission, the Scottsboro InSPIRESS Team 2 ATLAS (Assessing Titan’s Lakes by Air and Sea) was given the task by UAH of aiding the mission by designing a payload probe to accomplish further scientific analysis of the moon. To accomplish this assignment, ATLAS will perform an innovative experiment that would not be redundant to the TEAM mission, while providing results that further the understanding of Titan’s hydrocarbon lakes and aid the survivability of future missions. ATLAS developed a straightforward and efficient two-probe mission to compare Titan’s largest northern lake, Kraken Mare, and largest southern lake, Ontario Lacus, as well as determine the depths of the two lakes. Identical probes Peary (Kraken Mare) and Amundsen (Ontario Lacus) are designed to 1) Determine lake composition, 2) Measure lake pressure, 3) Measure speed, location, and direction, and 4) Measure lake temperature. 2.0 Science Objective and Instrumentation Probes Peary (named for Robert Peary, the first man to reach the North Pole on Earth) and Amundsen (named for Roald Amundsen, the first man to reach the South Pole on Earth) have one primary objective and one secondary objective for the ATLAS mission. -

A Assessment Study Report ESA Contribution to the Titan Saturn
ESA-SRE(2008)4 12 February 2009 N ITU LEMENTS ESA Contribution to the Titan Saturn System Mission Assessment Study Report a TSSM In Situ Elements issue 1 revision 2 - 12 February 2009 ESA-SRE(2008)4 page ii of vii C ONTRIBUTIONS This report is compiled from input by the following contributors: Titan-Saturn System Joint Science Definition Team (JSDT): Athéna Coustenis (Observatoire de Paris- Meudon, France; European Lead Scientist), Dennis Matson (JPL; NASA Study Scientist), Candice Hansen (JPL; NASA Deputy Study Scientist), Jonathan Lunine (University of Arizona; JSDT Co- Chair), Jean-Pierre Lebreton (ESA; JSDT Co-Chair), Lorenzo Bruzzone (University of Trento), Maria-Teresa Capria (Istituto di Astrofisica Spaziale, Rome), Julie Castillo-Rogez (JPL), Andrew Coates (Mullard Space Science Laboratory, Dorking), Michele K. Dougherty (Imperial College London), Andy Ingersoll (Caltech), Ralf Jaumann (DLR Institute of Planetary Research, Berlin), William Kurth (University of Iowa), Luisa M. Lara (Instituto de Astrofísica de Andalucía, Granada), Rosaly Lopes (JPL), Ralph Lorenz (JHU-APL), Chris McKay (Ames Research Center), Ingo Muller-Wodarg (Imperial College London), Olga Prieto-Ballesteros (Centro de Astrobiologia- INTA-CSIC, Madrid), François Raulin LISA (Université Paris 12 & Paris 7), Amy Simon-Miller (GSFC), Ed Sittler (GSFC), Jason Soderblom (University of Arizona), Frank Sohl (DLR Institute of Planetary Research, Berlin), Christophe Sotin (JPL), Dave Stevenson (Caltech), Ellen Stofan (Proxeny), Gabriel Tobie (Université de Nantes), Tetsuya -
TITAN SINCE APOLLO. R. D. Lorenz1, 1Johns Hopkins Applied Physics Laboratory, Laurel, MD 20723, USA
50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 1215.pdf TITAN SINCE APOLLO. R. D. Lorenz1, 1Johns Hopkins Applied Physics Laboratory, Laurel, MD 20723, USA. [email protected] Introduction – Titan circa 1970: Almost nothing 1994 showed bright and dark terrains at roughly the was known about Titan before Apollo, except the ex- resolution the naked eye sees our own moon, but inter- ceptional fact that it had an atmosphere! The state of pretation was challenging. Hubble data showed sea- the art – with Titan as a purely astronomical object - sonal change in the atmospheric haze, and as large was summarized in a 1973 workshop [1]. Polarimetry telescopes with adaptive optics systems emerged circa indicated the atmosphere was hazy, and the surface 2000, methane clouds were seen to come and go, sug- was speculated to be organic-rich and warmed by a gesting an active hydrological cycle. It was established greenhouse effect (figure 1). Debates about Titan's at this time that the biggest mysteries after Cassini climate mirrored those of Venus at the same period [2], would be the surface composition, and that surface and indeed the meagre spectroscopic data available on mobility would be a key capability [3,4]. Titan then is similar to the current state of knowledge Cassini-Huygens – A World at Last: Beginning of best-studied exoplanets. in 2004, Cassini data began to reveal ever-increasing areas of Titan's surface at high resolution, both in the near-infrared (ISS and VIMS) and with RADAR. The details were initially inscrutable but intriguing. The Huygens descent in January 2005 was much easier to interpret – the landing site was evidently a streambed (figure 2), and the channel networks seen from above and dampness in the ground attested to at least episodic and recent fluvial activity e.g.