Spatial Dependence in a Hedonic Real Estate Model: Evidence from Jamaica
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Update on Systems Subsequent to Tropical Storm Grace
Update on Systems subsequent to Tropical Storm Grace KSA NAME AREA SERVED STATUS East Gordon Town Relift Gordon Town and Kintyre JPS Single Phase Up Park Camp Well Up Park Camp, Sections of Vineyard Town Currently down - Investigation pending August Town, Hope Flats, Papine, Gordon Town, Mona Heights, Hope Road, Beverly Hills, Hope Pastures, Ravina, Hope Filter Plant Liguanea, Up Park Camp, Sections of Barbican Road Low Voltage Harbour View, Palisadoes, Port Royal, Seven Miles, Long Mountain Bayshore Power Outage Sections of Jack's Hill Road, Skyline Drive, Mountain Jubba Spring Booster Spring, Scott Level Road, Peter's Log No power due to fallen pipe West Constant Spring, Norbrook, Cherry Gardens, Havendale, Half-Way-Tree, Lady Musgrave, Liguanea, Manor Park, Shortwood, Graham Heights, Aylsham, Allerdyce, Arcadia, White Hall Gardens, Belgrade, Kingswood, Riva Ridge, Eastwood Park Gardens, Hughenden, Stillwell Road, Barbican Road, Russell Heights Constant Spring Road & Low Inflows. Intakes currently being Gardens, Camperdown, Mannings Hill Road, Red Hills cleaned Road, Arlene Gardens, Roehampton, Smokey Vale, Constant Spring Golf Club, Lower Jacks Hill Road, Jacks Hill, Tavistock, Trench Town, Calabar Mews, Zaidie Gardens, State Gardens, Haven Meade Relift, Hydra Drive Constant Spring Filter Plant Relift, Chancery Hall, Norbrook Tank To Forrest Hills Relift, Kirkland Relift, Brentwood Relift.Rock Pond, Red Hills, Brentwood, Leas Flat, Belvedere, Mosquito Valley, Sterling Castle, Forrest Hills, Forrest Hills Brentwood Relift, Kirkland -
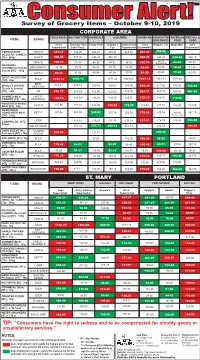
Survey of Grocery Items – October 9-10, 2019
Survey of Grocery Items – October 9-10, 2019 CORPORATE AREA CROSS ROADS HALF-WAY TREE HAVENDALE LIGUANEA BARBICAN WASHINGTON WATERLOO RED HILLS ITEMS BRAND BOULEVARD ROAD ROAD Hi-Lo Brooklyn (Twin Family Pride Shopper’s General Food Hi-Lo Shopper’s Fair Mega Mart Xxtra Supermarket Gates Plaza) Fair Supermarket Supermarket Supermarket 355.88 CORNED BEEF GRACE 457.37 432.20 386.41 428.78 428.78 457.37 (On Special) (REGULAR, CANNED) [TX] - 340g LASCO 368.22 347.96 345.20 345.20 368.22 345.20 344.84 345.19 84.76 GRACE 102.74 85.44 99.30 90.02 96.32 102.74 (On Special) 84.00 86.75 MACKEREL (CANNED) (In Tomato BRUNSWICK 83.99 79.39 78.76 78.76 78.76 85.60 78.76 78.00 81.90 Sauce) [NT] - 155g LASCO 86.38 81.62 80.98 80.98 80.98 86.38 80.98 77.00 81.00 DRIED SALTED FISH BULK 1060.15 1071.22 1063.65 1187.14 1067.72 1071.80 [TX] - 1kg 1187.14 BEST 528.21 539.83 WHOLE CHICKEN DRESSED 520.05 520.60 509.00 549.00 512.80 528.00 508.80 (Grade A, Frozen) (On Special) [NT] - 1kg CB 536.77 520.69 505.40 528.50 509.00 536.77 520.70 530.00 481.00 SKIMMED MILK LASCO - 123.83 126.01 119.70 126.01 132.13 119.70 119.00 POWDER [TX] - 80g READIMILK 132.13 POWDERED WHOLE 137.96 128.63 127.62 MILK [NT] - 80g LASCO 123.90 148.68 118.25 127.84 125.80 123.00 SWEETENED CONDENSED MILK BETTY 267.88 258.02 245.92 255.78 256.20 278.60 250.74 249.00 261.19 [TX] - 395g (On Special) LIDER 210.28 216.78 210.28 237.57 216.78 216.00 203.80 COOKING OIL [NT] - 218.52 500mL UNCLE SAM'S 202.33 200.73 200.73 201.74 204.74 204.75 DARK SUGAR (Pre- GOLDEN 219.54 211.31 200.00 Packaged) [NT] - 1kg GROVE RICE (WHITE) [NT] - 1kg BULK 97.67 102.50 108.30 96.39 98.60 CORNMEAL (Bulk) 110.45 84.01 84.01 87.50 103.15 [NT] - 1kg BULK 84.01 92.40 110.45 95.00 91.11 105.56 91.11 102.78 95.00 96.55 COUNTER FLOUR BULK 124.99 104.00 [NT] - 1kg JF MILLS 170.30 165.06 163.75 163.75 163.75 170.30 163.75 163.50 163.75 HARDOUGH BREAD 320.00 320.00 320.00 320.00 320.00 320.00 320.00 [NT] - 2 "lb" loaf NATIONAL 320.00 WATER CRACKERS 158.41 [NT] - 336 g EXCELSIOR 176.00 165.00 157.14 165.00 176.00 165.00 156.00 163.45 ST. -

Kingston and St. Andrew Water Supply Schedule
MAY 7, 2019 KINGSTON AND ST. ANDREW WATER SUPPLY SCHEDULE Water Supply Scheduled Times of Areas to be Supplied System Supply Havendale/Chancery 10:00 p.m. – 10:00 a.m. Havendale, Havenmead, Smokey Vale, Hydra Hall Daily Drive Relift, Ursa Major, Belgrade Heights, West Meade, Roehampton circle. Valve Operations 09:00 p.m. – 04:00 a.m. Cookhamdene, Tavistock, Millsborough Lower Jacks Hill Daily Valve Operations 04:00a.m – 09:00pm Barbican, Paddington Terrace and Dillsbury Lower Jacks Hill Daily Avenue Forest Hills 4:00 a.m. – 10:00 a.m. Meadowbrook Estate, Perkins Boulevard, Daily Queensborough, Abberville Avenue, Duhaney 4:00 p.m. – 10:00 p.m. Drive, Patrick City. Daily Constant Spring 10:00 p.m. – 10:00 a.m. Constant Spring Gardens, Upper Manning’s Hill (Restrict at Grants Daily Road, Crane Ave, Upper section of Valentines Pen) Gardens, Upper section of Red Hills Road. White Hall Gardens, , Wayne Close, Beverly Dale, Whitehall, Merrivale, Calabar Mews and Roads Leading Off Constant Spring Monday, Wednesday, Grosvenor Heights, Mannings Hill Road and (Restrict at Manor Friday Roads Leading Off Park) (based on fluctuations in production) Constant Monday, Wednesday, Cassia Park, Moreton Park and Roads leading Spring/Molynes Friday Off Booster Constant Monday, Wednesday, Olympic Gardens, Seaward Drive, Waltham Spring/Mona Friday and Sundays Park, Bayfarm, Cockburn Gardens, Seivwright Gardens Constant Spring/ New connection supplied Penwood Avenue, Bayfarm Road, and Roads Boulevard daily Leading Off Constant Tuesday, Thursday, Molynes Road, Ziadie Gardens, State Gardens, Spring/Mona Saturdays Dunrobin Avenue, Dunrobin Court* (Trucking based on fluctuations in production) *2 1000 gallons tanks were delivered to Dunrobin Court to alleviate supply issues Constant Spring Alternate Days 6:00 am to Trench Town, Jones Town, Arnett Gardens Supply from 8:00 pm Montgomery Corner Tank Mona 04:00 a.m. -

CAC Mobile App to Locate the Lowest Prices in Your Area and Help You Stay on Budget”
Survey of Grocery Items – January 6-7, 2021 CORPORATE AREA HALF-WAY HAVENDALE WATERLOO LIGUANEA MEADOWBROOK CONSTANT NEW STONY HILL RED HILLS ITEMS BRAND TREE ROAD SPRING KINGSTON & ENVIRONS ROAD Brooklyn (Twin Family Mega Mart Shopper’s Shoppers Delite Hi-Lo Supermarket John R Wong Master Mac Lee’s Food Gates Plaza) Pride Fair Supermarket Manor Park Plaza Supermarket Supermarket Fair (Formerly Joong) CORNED BEEF (REGULAR, LASCO 367.53 364.61 387.55 363.48 345.78 364.67 CANNED) [TX] - 340g 364.61 MACKEREL (CANNED) (In GRACE 99.00 110.06 106.00 104.66 107.91 111.64 106.70 104.29 114.50 Tomato Sauce) [NT] - 155g BRUNSWICK 155.70 154.46 154.00 154.46 159.96 157.45 150.76 154.50 SARDINES (CANNED, (Canadian Style) In Oil) [NT] - 106g GRACE 137.50 152.86 148.00 143.28 152.83 139.05 144.85 152.90 DRIED SALTED FISH [TX] - 1kg BULK 1275.44 1234.53 1121.25 1188.41 1218.00 1298.35 1372.64 1070.37 1218.77 WHOLE CHICKEN BEST DRESSED 592.91 575.00 592.00 539.96 549.00 592.90 543.44 550.56 (Grade A, Frozen) [NT] 1kg CB 548.10 575.00 571.80 635.25 557.00 564.55 551.29 564.53 POWDERED WHOLE MILK [NT] - 80g LASCO 122.53 121.57 121.00 127.62 139.79 118.65 124.50 SWEETENED CONDENSED MILK BETTY 279.20 270.17 285.20 275.49 275.49 294.32 298.31 274.70 292.79 [TX] - 395g (On Special) INFANT FORMULA NESTLE 787.63 750.06 781.38 714.39 744.16 743.55 732.12 762.10 [NT] - 400g LACTOGEN 1 COOKING OIL [NT] - 500mL LIDER 234.94 233.07 227.00 233.07 228.41 241.15 218.38 223.80 DARK SUGAR (Pre- Packaged) [NT] - 1kg JAMAICA GOLD 246.88 246.00 246.88 263.33 251.61 252.80 -

MINISTRY of JUSTICE Justice of the Peace Listing (St. Andrew)
MINISTRY OF JUSTICE Justice of the Peace Listing (St. Andrew) Surname Christian Name Street Area Contact Number ABEL Wendel Dwight Lot 10 Woodland Heights Red Hills 945-9672/869-9757 ABRAHAMS Newton 11 Green Glebe Road Forrest Hill 944-9597 AFFLICK-MITCHELL Aleathia Everst Apt. Old Stony Hill Road AIKEN Etheline 5 Miraflores Drive Kingston 20 925-4003/812-9332 AIKEN Liston 8 Sullivan Close AIKEN-DAVIS Yvette AITCHESON Salma Theresa Townhouse #5 42 Portview Road 926-4826/999-4227 AKWA Anette Angela 1A Waterworks Road Kingston 8 931-9639/843-8314 ALBERGA Lloyd Harcourt 3 Kingsway Apt. #6 928-1248/926-8850 ALEXANDER M. 17 Stars Way Kingston 20 969-0483/969-1414 ALEXANDER Penelope 3 Gerbera Close Kingston 6 970-0220 / 773-2209 ALLEN Faye Elaine Mount Joy, Old Stony Hill Road Kingston 9 9429168/9974540 ALLEN Gary Hugh 10 Edam Drive Kingston 8 969-6343/878-2201 ALLEN Cecil Lloyd 16 Norbury Close Kingston 8 9252653/9265369 ALLEN Rickert 21 Liguanea Ave Kingston 6 978-1633/935-2087/361-2687 ALLEN Delroy 45-47 Binns Road Kingston 11 779-7708/967-1848/571-9351 ALLEN Roy 7G Kew Lane 436-2577 ALLEN-KNIGHT Sandra 11 Zaidie Avenue 508-9540 ALLEN-SMITH Mary 6A Queens Way ALLMAN Melbourne P.O. Box 16 Red Hills 9445071/3998405 ALSTON Sharron 5 Madison Drive ANDERSON Joan 116 Weymouth Drive Kingston 20 ANDERSON Jenetia (Mrs.) 19 Glenhope Ave Kingston 6 399-2059/926-2008 Anderson Shynelle 9 Ixora Close Oakland 1 | P a g e ANDERSON Sylvester 21 Greendale Drive Valentine Gardens 781-0720 ANDRADE Jean M. -

MISCELLANEOUS TERRITORIES 2011.Doc
JAMAICA #317 #565 BARRETT, Veda ALMON, Winifred Savannah-La-Mar P.O. Box 18 Lot 6, Balm Subdivision Westmoreland Bog Walk P.O. Jamaica St. Catherine Tele: 876- 952 4001 (H) Jamaica 876- 952-0029 (W) Tele: 876-985 1145 (H) 876-927 1680 (W) #567 Email: [email protected] BARTLEY, Claudette A. Lot 144, Parakeet Drive #228 Priddes Housing Scheme ARTHURS, Geraldine P.O. Box 438, May Pen Lot 511, Eltham View Clarendon Brunswick, Jamaica Spanish Town P.O. Tele: 876-986 2483 (W) St. Catherine Jamaica #224 Tele: 876- 983 5180 (H) BARTLEY, Gelefer 876- 928 1137 (W) 73 Marine Drive Bridgeport P.O. #643 St. Catherine BAILY, Danette Jamaica #2907 Falmouth West Waterford PO Tele: 876-998 3018 (H) St. Catherine 876-512 2424 (W) Jamaica Shortwood Teachers, College (student) #665 77 Shortwood Road BECKER, Jill Kingston 8 390 Mchaf Drive Jamaica Bridge View Tele: 876-837 3211 Bridgeport P.O. St. Catherine #306 Jamaica BARRETT, Margarita Webb Road #568 Christiana P.O., BLAKE, Marcella E. Manchester Lot 29, Maise Cres., Fairview Park Jamaica Spanish Town P.O. Tele: 876-964 2305 (H) St. Catherine 876-987 8047-8 (W) Jamaica Tele: 876-981 3036 (H) #353 876- 927 1680-8 (W) BARRETT, Sheila Email: [email protected] c/o Mico Teachers’ College Marescaux Road, Kingston 5 Jamaica Tele: 876-929 5260-6 (W) #698 #700 BLAKE, Shina BROWN, Marsha Newel District Gloucester District Watchwell Thompson Town St Elizabeth Clarendon Jamaica Jamaica Tele: 876-474 1720 (H) Email: [email protected] # 725 BROWNE-WILSON, Claudia 20 Readers Pen #786 Mourant Bay BRAMWELL, Belinda St Thomas Lamb Town Jamaica Knockpatrick Tele: 876-929 5290 Mandeville Email: [email protected] Jamaica Tele: 876-904-9450 (H) #571 523-2073 (W) CAMPBELL, Joyce Email: [email protected] 4 Barbican Close Kingston 6 #644 Jamaica BRISSETT, Vivia Tele: 876- 927 4476 (H); White River Buff Bay PO 876- 926 6388 (W) Portland Fax: 876- 926 5545 Jamaica E-mail: [email protected] BURNETT Pamella #72 Lot 12 CAMPBELL, Versada Woodlawn Housing 23 Stockfarm Road Mandeville Golden Spring Jamaica P.O. -
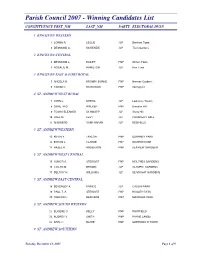
Winning Candidates List
Parish Council 2007 - Winning Candidates List CONSTITUENCY FRST_NM LAST_NM PARTY ELECTORAL DVSN 1 KINGSTON WESTERN 1 LORNA R. LESLIE JLP Denham Town 2 DESMOND A. MCKENZIE JLP Tivoli Gardens 2 KINGSTON CENTRAL 3 DESMOND L. BAILEY PNP Allman Town 4 ROSALIE M. HAMILTON JLP Rae Town 3 KINGSTON EAST & PORT ROYAL 5 ANGELA R. BROWN- BURKE PNP Norman Gardens 6FABIAN C. MCGOWAN PNP Springfield 4 ST. ANDREW WEST RURAL 7 JOHN L. MYERS JLP Lawrence Tavern 8 GARETH G. WALKER PNP Brandon Hill 9TOSHA ELEANOR SCHWAPP JLP Stony Hill 10 JOEL M. LEVY JLP CHANCERY HALL 11 ANSWERD RAMCHARAN JLP RED HILLS 5 ST. ANDREW WESTERN 12KEVIN Y. TAYLOR PNP DUHANEY PARK 13 BYRON L. CLARKE PNP WATERHOUSE 14 HAZEL H. ANDERSON PNP SEAVIEW GARDENS 6 ST. ANDREW WEST CENTRAL 15 JUNIOR A. STEWART PNP MOLYNES GARDENS 16 CISLYN M. BROWN JLP OLYMPIC GARDENS 17 DELROY H. WILLIAMS JLP SEIVRIGHT GARDENS 7 ST. ANDREW EAST CENTRAL 18BEVERLEY A. PRINCE JLP CASSIA PARK 19PAUL T. A. STEWART PNP HAGLEY PARK 20 TREVOR L. BERNARD PNP MAXFIELD PARK 8 ST. ANDREW SOUTH WESTERN 21EUGENE O. KELLY PNP WHITFIELD 22 AUDREY V. SMITH PNP PAYNE LANDS 23 KARL C. BLAKE PNP GREENWICH TOWN 9 ST. ANDREW SOUTHERN Tuesday, December 11, 2007 Page 1 of 9 Parish Council 2007 - Winning Candidates List CONSTITUENCY FRST_NM LAST_NM PARTY ELECTORAL DVSN 24 NEVILLE I. WRIGHT PNP TRENCH TOWN 25 MARCIA E. NEITA PNP ADMIRAL TOWN 10 ST. ANDREW SOUTH EASTERN 26 WADEROY I. C. CLARKE JLP TRAFALGAR ROAD 27ANDREW A. SWABY PNP VINEYARD TOWN 11 ST. ANDREW EASTERN 28 GEORGE A. -

MINISTRY of JUSTICE Justice of the Peace Listing (Kingston)
MINISTRY OF JUSTICE Justice of the Peace Listing (Kingston) Surname First Name Contact Number Address ABBOTT April Aretha 928-6231-5 (W); 565-7385 (H); 9 St Georges Road, Kingston 2 565-7385 (M) ADAMS Winston Ivanhoe (Dr) 929-2367, 665-3000 (W); 755- 9 Norbrook Way, Kingston 8 5050 (H); 899-5987 (M) AIKEN Horace Orlando (Rev) 875-7183 (W); 382-2143 (H); 16 Constant Spring Grove, 427-8221 (M) Kingston 8 AJAGUNNA Ibrahim Aladeusi (Dr) 924-8150, 924-8159 (W); 928- 4 Courtney Avenue, Kingston 3 4145 (H); 898-2949, 564-4494 (M) ALEXANDER Mark Dean 968-7734 (W); 909-4078 (H); 1 Allerdyce Close, Kingston 8 840-4078 (M) ALEXANDER Uriah Phillip 925-0816 (H); 999-2216 (M) 1A Norbrook Road, Townhouse No. 28, Kingston 8 ALLEN Audrey Andria 928-4955 (W); 758-0018 (H); 18 Canary Avenue, Sievright 298-4564, 346-3189 (M) Gardens, Kingston 11 ALLEN Barbara Annette 502-5840, 612-5840 (W); 749- 32 Bonitto Avenue, Tryall 3170 (H); 000-0000 (M) Estate, Spanish Town, St Catherine ALLEN Clinton Dudley 2 Gibson Road, PO Box 1180, Kingston 8 ALLEN Enoch Nathaniel 922-9105-9 (W); 532-7471, 868- 4 Topaz Way, Eltham Park, 4503 (M) Spanish Town, St Catherine ALLEN Lincoln Antonio 619-6063, 564-2458 (W); 851- 18 University Close, College 1925 (M) Common, Kingston 7 ALLEN Pandita Monica 929-6694, 908-3731 (W); 938- 30 Merrion Road, Vineyard 3711 (H); 000-0000 (M) Town, Kingston 3 ALLEN Rockey Charles 901-3344, 631-2645, 2646 (W); 9 Knightsdale Drive, Knights 847-2067 (M) Bridge, Apartment No 10, Kingston 19 ALLEN-WANLISS O’Kenio Kenai 665-4357, 665-3700 (W); 846- 119 -

Jamaica: Hurricane Matthew- Assessment Planning Map 1 of 12
# # # 290000 300000 310000 320000 # 330000 u"# 340000 MA00##3_1 # "# 0 " u Shotover P !P 0 N u ! 0 ' ! v® 0 0 u"S 1 1 u" ! ° u" # 0 8 # 2 1 # S a ii n tt u" # # # M a rr y u"# u" !#S u" # # u" # #Silver # # # # u" # !Berridale !Hill # # # # # !S !S # u" # #" # u" u# u" # # u" # # P o rr tt ll a n d ! S # o !#S # #S u"Bog Walk ! # # u" # u"# u"# u" N ' 5 # ° # # 0 8 # 0 1 u" 0 # # # 0 u"# # St. 0 " 0 u 2 S a ii n tt !Peter's Smokey A n d rr e w # "Vale The Red "Rockhamptons !Light # # # " S a ii n tt u" " Constant # u Have"ndale Norbrook # Penlyne Spr" ing # C a t h e r i n e #S Castle C a t h e r i n e Plantation ! Constant Spring Valentine ## # # !# "Grove " Gordon u" " "Heights " "Gardens # Cherry A" ngels Estates 2 " #!S " The Town Duhaney Victoria " Meadowbu"rook Gardens u"! Mavis Co!operage Caymanas #!S " Court !P # # P" ark Bank Eltham " Patrick # "Barbican Country Club S#u u" # !# #S !S# #S # # u"! " Park Ci!ty ! "Ferry # # # Fairview "Estates # # " Riverton # S " # u" ! # Hagley " S Park/Friendship Me"adows Keystone # #! u" # # " "City u" Liguanea P Gap " # # Mona ! Ebony Eltham# # S #Half Way #u" u" " !S ! ! " "Heights Ensom # St Jago # u Hyde # # "Tree " V" ale Acres # Arntally " S u" S# City" ! New ! # S " 31 St. !# Heights "Park Richmond v®v® # ! Royale Place Estate " Hamilton # " # Lauriston # "Kingston Central Christian u" " Park # N John's u" " " ° Green Innswood Gardens Three S Long Mouu"ntva®#in 8 # Greendale Vi" llage S # " ! S#Ro" ad S Gardens ! S " 1 !S ! # ! # # # " S Country Club ! Miles " Acres "Estates # #" # " -

Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized
Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized 1 Acknowledgements This technical report is a joint product of the Planning Institute of Jamaica (PIOJ) and the Statistical Institute of Jamaica (STATIN), with support from the World Bank. The core task team at PIOJ consisted of Caren Nelson (Director, Policy Research Unit), Christopher O’Connor (Policy Analyst), Hugh Morris (Director, Modelling & Research Unit), Jumaine Taylor (Senior Economist), Frederick Gordon (Director, JamStats), Patrine Cole (GIS Analysit), and Suzette Johnson (Senior Policy Analyst), while Roxine Ricketts provided administrative support. The core task team at STATIN consisted of Leesha Delatie-Budair (Deputy Director General), Jessica Campbell (Senior Statistician), Kadi-Ann Hinds (Senior Statistician), Martin Brown (Senior Statistician), Amanda Lee (Statistician), O’Dayne Plummer (Statistician), Sue Yuen Lue Lim (Statistician), and Mirko Morant (Geographer). The core task team at the World Bank consisted of Juan Carlos Parra (Senior Economist) and Eduardo Ortiz (Consultant). Nubuo Yoshida (Lead Economist) and Maria Eugenia Genoni (Senior Economist) provided guidance and comments to previous versions of this report. The team benefited from the support and guidance provided by Carol Coy (Director General, STATIN) and Galina Sotirova (Country Manager, World Bank). We also want to thank the Geographical Services Unit in STATIN for drawing the final maps. 2 Methodology and data sources This document -

MINISTRY of JUSTICE Justice of the Peace Listing (Kingston)
MINISTRY OF JUSTICE Justice of the Peace Listing (Kingston) Surname Christian and Middle Street Area Contact Number Names ABBOTT April Aretha Caribbean Cement Co Ltd, 9 St Georges Road, Kingston 928-6231-5 (W); 565-7385 (H); 565- Rockfort, Kingston 2 2 7385 (M) ADAMS Winston Ivanhoe (Dr) University College of the 9 Norbrook Way, Kingston 8 929-2367, 665-3000 (W); 755-5050 Caribbean, 17 Worthington (H); 899-5987 (M) Avenue, Kingston 5 AIKEN Horace Orlando (Rev) Kintyre New Testament Church 16 Constant Spring Grove, 875-7183 (W); 382-2143 (H); 427- of God, 176 Housing Drive, Kingston 8 8221 (M) Kingston 7 AJAGUNNA Ibrahim Aladeusi (Dr) Caribbean Maritime Institute, 4 Courtney Avenue, Kingston 924-8150, 924-8159 (W); 928-4145 Palisadoes Park, Kingston 17 3 (H); 898-2949, 564-4494 (M) ALEXANDER Mark Dean New Auto Zone Limited, 22 1 Allerdyce Close, Kingston 8 968-7734 (W); 909-4078 (H); 840- Burlington Avenue, Kingston 10 4078 (M) ALEXANDER Uriah Phillip N/A 1A Norbrook Road, 925-0816 (H); 999-2216 (M) Townhouse No. 28, Kingston 8 ALLEN Audrey Andria Ministry of Health, St Joseph's 18 Canary Avenue, Sievright 928-4955 (W); 758-0018 (H); 298- Hospital, 22 Deanery Road, Gardens, Kingston 11 4564, 346-3189 (M) Kingston 3 ALLEN Barbara Annette Ministry of Education, Youth 32 Bonitto Avenue, Tryall 502-5840, 612-5840 (W); 749-3170 and Information, Planning and Estate, Spanish Town, St (H); 000-0000 (M) Development Division, 2-4 Catherine National Heroes' Circle, Kingston 4 ALLEN Enoch Nathaniel International Seabed Authority, 4 Topaz Way, Eltham Park, 922-9105-9 (W); 532-7471, 868- 14-20 Port Royal Street, Spanish Town, St Catherine 4503 (M) Kingston 1 | P a g e ALLEN Gladstone Anthony Jamaica Defence Force Air 926 8121-9 Ext 2134. -

Padmore Havendale
ST.ANDREW Golden Spring - Mt. Airy Norbrook - Woodford Swain Spring - Padmore Havendale - Guava Gap Barbican - Skyline Drive Guava Ridge - Cooperage Harbour View - Bull Bay Turn Bridge - Santa Maria Constant Spring - Stony Hill Old Stony Hill Road Cassia Park Avenue Cassia Park Road Lindsay Terrace Surbiton Avenue Waltham Park Road Whitehall Avenue Dumbarton Avenue Westminister Road (Between Cassia Park Avenue and Dumbarton Avenue) Princess Street Spanish Town Road East Road Norway Terrace (Norbrook) Elena Crescent Warminister Avenue Crane Avenue & Crane Crescent Morant Avenue KINGSTON Washington Boulevard Coleyville Avenue Padmore Drive Duhaney Drive Baldwin Crescent Jacks Hill Port Royal Road Windward Road Mountain View Avenue Cherry Drive Merrion Road Wedcombe Avenue Fairway Avenue Windsor Avenue Downer Avenue Hope Road Winchester Road Victoria Street Victoria Avenue John Golding Avenue Ottawa Avenue Gordon Town Road/Papine Square Mona Road Charlemont Drive Jack's Hill - Skyline Drive King's House Avenue Red Hills Road (from Meadobrook Avenue to the foot of Red Hills) Molynes Road Arnold Road North Avenue (Swallowfield) Author Wint Drive Daytona Drive Bretford Avenue ST. THOMAS Port Mornat - Pleasant Hill Pleasant Hill - Hetcors River Morant Bay - Port Morant Port Morant - Bath (Curtis Bottom) Morant Bay - Wilmington (Starton HS) Morant Bay - Port Morant (Top Hill) Golden Grove - Hampton Court Hampton Court - Dalvey Bath - Hordley Wheelersfield - Cedar Grove Morant Bay - Wilming ton Bull Bay - Grants Pen Grants Pen - Pamphret Pamphret