Designof a Candidateflutter Suppression Control Law for Dast Arw-2
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Framework for In-Field Analyses of Performance and Sub-Technique Selection in Standing Para Cross-Country Skiers
sensors Article Framework for In-Field Analyses of Performance and Sub-Technique Selection in Standing Para Cross-Country Skiers Camilla H. Carlsen 1,*, Julia Kathrin Baumgart 1, Jan Kocbach 1,2, Pål Haugnes 1 , Evy M. B. Paulussen 1,3 and Øyvind Sandbakk 1 1 Centre for Elite Sports Research, Department of Neuromedicine and Movement Science, Faculty of Medicine and Health Sciences, Norwegian University of Science and Technology, 7491 Trondheim, Norway; [email protected] (J.K.B.); [email protected] (J.K.); [email protected] (P.H.); [email protected] (E.M.B.P.); [email protected] (Ø.S.) 2 NORCE Norwegian Research Centre AS, 5008 Bergen, Norway 3 Faculty of Health, Medicine & Life Sciences, Maastricht University, 6200 MD Maastricht, The Netherlands * Correspondence: [email protected]; Tel.: +47-452-40-788 Abstract: Our aims were to evaluate the feasibility of a framework based on micro-sensor technology for in-field analyses of performance and sub-technique selection in Para cross-country (XC) skiing by using it to compare these parameters between elite standing Para (two men; one woman) and able- bodied (AB) (three men; four women) XC skiers during a classical skiing race. The data from a global navigation satellite system and inertial measurement unit were integrated to compare time loss and selected sub-techniques as a function of speed. Compared to male/female AB skiers, male/female Para skiers displayed 19/14% slower average speed with the largest time loss (65 ± 36/35 ± 6 s/lap) Citation: Carlsen, C.H.; Kathrin found in uphill terrain. -

Design of Control Laws for Flutter Suppression Based on the Aerodynamic Energy Concept and Comparisons with Other Design Methods
NASA Technical Paper 3056 1990 Design of Control Laws for Flutter Suppression Based on the Aerodynamic Energy Concept and Comparisons With Other Design Methods E. Nissim Ames Research Center Dryden Flight Research Facility Edwards, California National Aeronautics and Space Administration Office of Management Scientific and Technical Information Division CONTENTS SUMMARY INTRODUCTION NOMENCLATURE 2 Abbreviations ............................................... 2 2 Letter and Mathematical Symbols ..................................... Subscripts ................................................. 3 REVIEW OF AERODYNAMIC ENERGY CONCEPT 3 3 General Approach ............................................. Review of Aerodynamic Energy Two-Dimensional Strip Results ..................... 4 Review of Specific Control Laws Obtained Using the Aerodynamic Energy Concept ........... 5 Review of Control Law Synthesis Technique ............................... 6 DAST-ARW1 MODEL 7 Description ................................................. 7 Validation ................................................. 7 DEVELOPMENT AND EVALUATION OF IMPROVED CONTROL LAW SYNTHESIS TECHNIQUE 9 Case 1--Synthesis Technique and Presentation of Results for Systems With No Actuator Dynamics . 9 Case 2----Control Laws Synthesized With Actuator and With Structural Filter ............... 12 Definition of the Form of the Required Control Law ......................... 12 Presentation of Results ........................................ 13 Case 3--Results for Systems With Actuator Only, -

National Classification? 13
NATIONAL CL ASSIFICATION INFORMATION FOR MULTI CLASS SWIMMERS Version 1.2 2019 PRINCIPAL PARTNER MAJOR PARTNERS CLASSIFICATION PARTNERS Version 1.2 2019 National Swimming Classification Information for Multi Class Swimmers 1 CONTENTS TERMINOLOGY 3 WHAT IS CLASSIFICATION? 4 WHAT IS THE CLASSIFICATION PATHWAY? 4 WHAT ARE THE ELIGIBLE IMPAIRMENTS? 5 CLASSIFICATION SYSTEMS 6 CLASSIFICATION SYSTEM PARTNERS 6 WHAT IS A SPORT CLASS? 7 HOW IS A SPORT CLASS ALLOCATED TO AN ATHLETE? 7 WHAT ARE THE SPORT CLASSES IN MULTI CLASS SWIMMING? 8 SPORT CLASS STATUS 11 CODES OF EXCEPTION 12 HOW DO I CHECK MY NATIONAL CLASSIFICATION? 13 HOW DO I GET A NATIONAL CLASSIFICATION? 13 MORE INFORMATION 14 CONTACT INFORMATION 16 Version 1.2 2019 National Swimming Classification Information for Multi Class Swimmers 2 TERMINOLOGY Assessment Specific clinical procedure conducted during athlete evaluation processes ATG Australian Transplant Games SIA Sport Inclusion Australia BME Benchmark Event CISD The International Committee of Sports for the Deaf Classification Refers to the system of grouping athletes based on impact of impairment Classification Organisations with a responsibility for administering the swimming classification systems in System Partners Australia Deaflympian Representative at Deaflympic Games DPE Daily Performance Environment DSA Deaf Sports Australia Eligibility Criteria Requirements under which athletes are evaluated for a Sport Class Evaluation Process of determining if an athlete meets eligibility criteria for a Sport Class HI Hearing Impairment ICDS International Committee of Sports for the Deaf II Intellectual Impairment Inas International Federation for Sport for Para-athletes with an Intellectual Disability General term that refers to strategic initiatives that address engagement of targeted population Inclusion groups that typically face disadvantage, including people with disability. -

IGCC®/IGMA® CERTIFIED PRODUCTS February 2018 Page 15
IGCC®/IGMA® CERTIFIED PRODUCTS CERTIFICATION FRAME INTERNAL LICENSEE NUMBER CONSTRUCTION SUBSTRATE SPACER DESICCANT SEALANT COMPONENTS GCIA Advantage Glass Corp 4457 BC4/PLLC U/C2 ZS LF PIB/S2 601 West Carboy Road Mount Prospect, IL 60056 847-290-1707 Advantage Glass Corp. IGCC(R)IGMA(R) 2017 AGC Flat Glass (Thailand) PLC. 4432 MC4/ALK U/C3/U MA/MA LF/LF PIB/S2 Yes 200 Moo 1, Suksawad Road Pak Khlong Bang Pla Kod Phra Samut Chedi, Samut Prakan 10290 Thailand 66-2815-5000x1982 AGC/Poma Glass Co. N.A. 2903 BC3/MC1/ZS/IC U/C3/U UT/UT DM/DM HM IC Yes 365 McClurg Road-Suite E 2904 BC3/MC1/ZS/IC U/C3/U US/US DM/DM HM IC Yes Boardman, OH 44512 3705 BC3/MC1/MT/IC U/C3/U FS/FS IB/IB HM IC Yes 330-965-1000 4173 BC3/MC1/IC U/C3 BCS IB BCS IC Yes AGC 61 IGCC®/IGMA® 2017 4268 BC3/MC1/ZS/IC U/C3/U US/US DM/DM RHM IC Yes 4277 BC3/MC1/ZS/IC U/C3/U UT/UT DM/DM RHM IC Yes 4584 BC3/MC1/IC U/C3 BPS IB BPS IC Yes 4654 BC3/MC1/MT/IC U/C3 FS/FS IB/IB HM IC Yes 4655 BC3/MC1/IC U/C3/U BCS/BCS IB/IB BCS IC Yes AGC-Poma Glass Co. N.A. 3981 BC3/MC1/MT/IC U/C3/U FS/FS IB/IB HM IC Yes 480 California Road 3982 BC3/MC1/ZS/IC U/C3/U US/US DM/DM HM IC Quakertown, PA 18951 4093 BC3/MC1/ZS/IC U/C3/U UT/UT DM/DM HM IC 215-538-9424 4094 BC3/MC1/ZS/IC U/C3/U UT/UT DM/DM HM IC Yes AGC 63 IGCC(R)/IGMA(R) 17 4099 BC3/MC1/IC U/C3 BPS IB BPS IC Yes 4236 BC3/MC1/IC U/C3/U BCS/BCS IB/IB BCS IC Yes 4648 BC3/MC1/ZS/IC U/C3/U US/US DM/DM HM IC Yes 4673 BC3/MC1/MT/IC U/C3/U FS/FS IB/IB HM IC Yes 4674 BC3/MC1/IC U/C3 BPS IB BPS IC Yes 4675 BC3/MC1/IC U/C3/U BCS/BCS IB/IB BCS IC Yes Ajiya Safety Glass Sdn Bhd 2871 MC4/PLK U/C2 MA LF PIB/S2 Lot 575, 1 KM Lebuhraya Segamat-Kuantan Segamat, Johor 85000 Malaysia 607-9313133 Ajiya® IGCC®/IGMA® ASTM E2190 2017 Al Abbar Architectural Glass 2977 BC4/ALLC U/U MA LF PIB/S2 Yes Sanaa St., PO Box 1626 Ras Alkhor, Industrial Estate Dubai United Arab Emirates 104-333-1362 Al Abbar IGCC®/IGMA® 2017 February 2018 Page 15 CERTIFICATION FRAME INTERNAL LICENSEE NUMBER CONSTRUCTION SUBSTRATE SPACER DESICCANT SEALANT COMPONENTS GCIA Aldora Aluminum and Glass Products Inc. -

United States Olympic Committee and U.S. Department of Veterans Affairs
SELECTION STANDARDS United States Olympic Committee and U.S. Department of Veterans Affairs Veteran Monthly Assistance Allowance Program The U.S. Olympic Committee supports Paralympic-eligible military veterans in their efforts to represent the USA at the Paralympic Games and other international sport competitions. Veterans who demonstrate exceptional sport skills and the commitment necessary to pursue elite-level competition are given guidance on securing the training, support, and coaching needed to qualify for Team USA and achieve their Paralympic dreams. Through a partnership between the United States Department of Veterans Affairs and the USOC, the VA National Veterans Sports Programs & Special Events Office provides a monthly assistance allowance for disabled Veterans of the Armed Forces training in a Paralympic sport, as authorized by 38 U.S.C. § 322(d) and section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program the VA will pay a monthly allowance to a Veteran with a service-connected or non-service-connected disability if the Veteran meets the minimum VA Monthly Assistance Allowance (VMAA) Standard in his/her respective sport and sport class at a recognized competition. Athletes must have established training and competition plans and are responsible for turning in monthly and/or quarterly forms and reports in order to continue receiving the monthly assistance allowance. Additionally, an athlete must be U.S. citizen OR permanent resident to be eligible. Lastly, in order to be eligible for the VMAA athletes must undergo either national or international classification evaluation (and be found Paralympic sport eligible) within six months of being placed on the allowance pay list. -

(VA) Veteran Monthly Assistance Allowance for Disabled Veterans
Revised May 23, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L. -

Pushbuttons.Pdf
PushButtons2013Cover.QXD_CircuitBreakers_2006Cover.QXD 10/3/17 2:20 PM Page 1 Altech Corporation 35 Royal Road Flemington, NJ 08822-6000 P 908.806.9400 • F 908.806.9490 www.altechcorp.com Altech Corp.® 255-052013-3M Printed July 2013 AltechAltech CorporationCorporation Since 1984, Altech Corporation has grown to become a leading supplier of automation and industrial control components. Headquartered in Flemington, NJ, Altech has an experienced staff of engineering, manufacturing and sales personnel to provide the highest quality products with superior service. This is the Altech Commitment! Altech 22 and 30mm Push Buttons offer ideal cost-effective solutions for control circuits utilizing both direct and remote management applications. Ease of assembly has been engineered into the design; the only tool necessary for installation is a screwdriver. • LED Indicating Devices • Pilot Lights • Push Button Stations • Push Button Enclosures • UL Recognized • Custom Push Button Assemblies • All Very Competitively Priced Our well trained technical experts welcome the opportunity to answer your technical questions and provide solutions to your automation and control needs. Give us a call or visit www.altechcorp.com. Quality Commitment Altech’s control components meet diverse national and international standards such as UL, NEC, CSA, IEC, VDE and more. Altech provides superior customer service and delivery through Total Quality Management and Continuous Process Improvement. Altech is ISO 9001 approved. We perform these services with honesty and integrity -

A Strategy to Optimize the Generation of Stable Chromobody Cell Lines for Visualization and Quantification of Endogenous Proteins in Living Cells
Supplementary: A strategy to optimize the generation of stable chromobody cell lines for visualization and quantification of endogenous proteins in living cells Bettina-Maria Keller1, Julia Maier1, Melissa Weldle1, Soeren Segan2, Bjoern Traenkle1, Ulrich Rothbauer1,2* 1 Pharmaceutical Biotechnology, Eberhard Karls University Tuebingen, Germany 2 Natural and Medical Sciences Institute at the University of Tuebingen, Reutlingen, Germany Correspondence: Prof. Dr. Ulrich Rothbauer, Natural and Medical Sciences Institute at the University of Tuebingen Markwiesenstr. 55, 72770 Reutlingen, Germany. E-mail: [email protected] Phone: +49 7121 51530-415 Fax: +49 7121 51530-816 Supplementary information DNA oligo name Sequence, 5’ - 3’ NB-ubi-for ATA TAT CTG CAG GAG TCT GGG GGA GGC TTG GTG CA NB-ubi-rev ATA TAT TCC GGA GGA GAC GGT GAC CTG GGT CCC β-actin-promoter-for GGA ATT AAT ACT GCC TGG CCA CTC CAT G β-actin-promoter-rev TCC GCT AGC TCG GCA AAG GCG AGG C β-actin-promoter-mutPstI-for AGA GCT CCT TGT GCA GGA GCG β-actin-promoter-mutPstI-rev TGG AGG GCA TGG AGT GGC AAVS1-CB-donor-fragment-2-for TAG AGG CGG CAA TTG TTC A AAVS1-CB-donor-fragment-2-rev TGT TGT TAA CTT GTT TAT TGC AGC Seq-AAVS1-CB-donor-1 TAT GGA AAA ACG CCA GCA AC Seq-AAVS1-CB-donor-2 ATG TGG CTC TGG TTC TGG G Seq-AAVS1-CB-donor-3 AGC GGC TCG GCT TCA C Seq-AAVS1-CB-donor-4 CCT TAG ATG TTT TAC TAG CCA GAT genPCR-AAVS1-int-for TCG ACT TCC CTT CTT CCG ATG genPCR-AAVS1-int-rev CTC AGA TTC TGG GAG AGG GTA EF1α-promoter (gBlock® gene TTACCGCCATGCATTAGTTATTAATGGCTCCGGTGCCCGTCAGTGGGCAGAGCGCACAT -

2019 Prohibited List
THE WORLD ANTI-DOPING CODE INTERNATIONAL STANDARD PROHIBITED LIST JANUARY 2019 The official text of the Prohibited List shall be maintained by WADA and shall be published in English and French. In the event of any conflict between the English and French versions, the English version shall prevail. This List shall come into effect on 1 January 2019 SUBSTANCES & METHODS PROHIBITED AT ALL TIMES (IN- AND OUT-OF-COMPETITION) IN ACCORDANCE WITH ARTICLE 4.2.2 OF THE WORLD ANTI-DOPING CODE, ALL PROHIBITED SUBSTANCES SHALL BE CONSIDERED AS “SPECIFIED SUBSTANCES” EXCEPT SUBSTANCES IN CLASSES S1, S2, S4.4, S4.5, S6.A, AND PROHIBITED METHODS M1, M2 AND M3. PROHIBITED SUBSTANCES NON-APPROVED SUBSTANCES Mestanolone; S0 Mesterolone; Any pharmacological substance which is not Metandienone (17β-hydroxy-17α-methylandrosta-1,4-dien- addressed by any of the subsequent sections of the 3-one); List and with no current approval by any governmental Metenolone; regulatory health authority for human therapeutic use Methandriol; (e.g. drugs under pre-clinical or clinical development Methasterone (17β-hydroxy-2α,17α-dimethyl-5α- or discontinued, designer drugs, substances approved androstan-3-one); only for veterinary use) is prohibited at all times. Methyldienolone (17β-hydroxy-17α-methylestra-4,9-dien- 3-one); ANABOLIC AGENTS Methyl-1-testosterone (17β-hydroxy-17α-methyl-5α- S1 androst-1-en-3-one); Anabolic agents are prohibited. Methylnortestosterone (17β-hydroxy-17α-methylestr-4-en- 3-one); 1. ANABOLIC ANDROGENIC STEROIDS (AAS) Methyltestosterone; a. Exogenous* -

UC Berkeley UC Berkeley Electronic Theses and Dissertations
UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Encapsulating Metal Clusters and Acid Sites within Small Voids: Synthetic Strategies and Catalytic Consequences Permalink https://escholarship.org/uc/item/8xv8d3dh Author Goel, Sarika Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Encapsulating Metal Clusters and Acid Sites within Small Voids: Synthetic Strategies and Catalytic Consequences by Sarika Goel A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Chemical Engineering in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Enrique Iglesia, Chair Professor Alexander Katz Professor Jeffrey R. Long Summer 2015 Encapsulating Metal Clusters and Acid Sites within Small Voids: Synthetic Strategies and Catalytic Consequences Copyright 2015 by Sarika Goel Abstract Encapsulating Metal Clusters and Acid Sites within Small Voids: Synthetic Strategies and Catalytic Consequences by Sarika Goel Doctor of Philosophy in Chemical Engineering University of California, Berkeley Professor Enrique Iglesia, Chair The selective encapsulation of metal clusters within zeolites can be used to prepare clusters that are uniform in diameter and to protect them against sintering and contact with feed impurities, while concurrently allowing active sites to select reactants based on their molecular size, thus conferring enzyme-like specificity to chemical -

Supporting Information
Supporting Information Direct Synthesis of Bulk Boron-Doped Graphitic Carbon Nicholas P. Stadie, Emanuel Billeter, Laura Piveteau, Kostiantyn V. Kravchyk, Max Döbeli, and Maksym V. Kovalenko Contents: Tables S1-S3. Acquisition parameters for 11B and 13C NMR experiments Figure S1. Photographs of precursors and BC3′ product 13 Figure S2. C MAS NMR spectrum of BC3′ Figure S3. Raman spectroscopy of reference materials Figure S4. XRD comparison between tiled BC3′ and BC3′ (this work) Figure S5. SEM comparison between tiled BC3′ and BC3′ (this work) Figure S6. Raman spectroscopy comparison between tiled BC3′ and BC3′ (this work) Figure S7. Raman spectroscopy analysis of various BC3′ materials 11 Figure S8. B MAS NMR comparison between tiled BC3′ and BC3′ (this work) Figures S9-S10. ERDA comparison between tiled BC3′ and BC3′ (this work) Table S1. Acquisition parameters for 11B MQMAS NMR (Figure 5) Magnetic Field (T) 16.4 Temperature (K) 298 Rotor Diameter (mm) 2.5 Pulse Sequence mp3qdfs (Bruker) Number of Scans 1664 Recycle Delay (s) 0.6 Direct Dimension: 100 Spectral Width (kHz) Indirect Dimension: 125 Spinning Frequency (kHz) 20 Direct Dimension: 1024 Acquisition Length (points) Indirect Dimension: 256 Rotor Cycles for Synchronization 40 Indirect Dimension Increment (µs) 8.0 Split-t1 Increment (µs) 6.2 11B Excitation Pulse Width [π/2] (µs) 4.5 Double Frequency Sweep Length (µs) 12.5 11B Selective Pulse Width [π] (µs) 42 Table S2. Acquisition parameters for 11B MAS NMR (Figure S7) Magnetic Field (T) 16.4 Temperature (K) 298 Rotor Diameter (mm) 2.5 Pulse Sequence hahnecho (Bruker) Number of Scans 304 Recycle Delay (s) 1 Spectral Width (kHz) 100 Spinning Frequency (kHz) 20 Acquisition Length (points) 2048 11B 90° Pulse Width [π/2] (µs) 22 Table S3. -
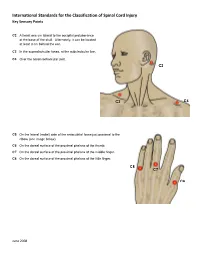
International Standards for the Classification of Spinal Cord Injury Key Sensory Points
International Standards for the Classification of Spinal Cord Injury Key Sensory Points C2 At least one cm lateral to the occipital protuberance at the base of the skull. Alternately, it can be located at least 3 cm behind the ear. C3 In the supraclavicular fossa, at the midclavicular line. C4 Over the acromioclavicular joint. C2 C3 C4 C5 On the lateral (radial) side of the antecubital fossa just proximal to the elbow (see image below). C6 On the dorsal surface of the proximal phalanx of the thumb. C7 On the dorsal surface of the proximal phalanx of the middle finger. C8 On the dorsal surface of the proximal phalanx of the little finger. C8 C7 C6 June 2008 International Standards for the Classification of Spinal Cord Injury Key Sensory Points C5 T2 T1 T1 On the medial (ulnar) side of the antecubital fossa, just proximal to the medial epicondyle of the humerus. T2 At the apex of the axilla. June 2008 International Standards for the Classification of Spinal Cord Injury Key Sensory Points T3 At the midclavicular line and the third intercostal space, found by palpating the anterior chest to locate the third C3 rib and the corresponding third intercostal space below it. T4 At the midclavicular line and the fourth intercostal space, located at the level of the nipples. T5 At the midclavicular line and the fifth intercostal space, located midway between the level of the nipples and T3 the level of the xiphisternum. T4 T6 At the midclavicular line, located at the level of the xiphisternum. T5 T7 At the midclavicular line, one quarter the distance between the level of T6 the xiphisternum and the level of the umbilicus.