DOCSLIB.ORG

Internal Model Control Approach to PI Tunning in Vector Control of Induction Motor

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Internal Model Control Approach to PI Tunning in Vector Control of Induction Motor International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 4 Issue 06, June-2015 Internal Model Control Approach to PI Tunning in Vector Control of Induction Motor Vipul G. Pagrut, Ragini V. Meshram, Bharat N. Gupta , Pranao Walekar Department of Electrical Engineering Veermata Jijabai Technological Institute Mumbai, India Abstract— This paper deals with the design of PI controllers 휓푟 Space phasor of rotor flux linkages to meet the desired torque and speed response of Induction motor 휓푑푟 Direct axis rotor flux linkages drive. Vector control oriented technique controls the speed and 휓 Quadrature axis flux linkages torque of induction motor separately. This algorithm is executed 푞푟 in two control loops, the current loop is fast innermost and outer 푇푟 Rotor time constant speed loop is slow compared to inner loop. Fast control loop 퐽 Motor Inertia executes two independent current control loop, are direct and quadrature axis current PI controllers. Direct axis current is used to control rotor magnetizing flux and quadrature axis II. INTRODUCTION current is to control motor torque. If the acceleration or HIGH-SPEED capability machines are needed in numerous deceleration rate is high and the flux variation is fast, then the applications for example, pumps, ac servo, traction and shaft flux of the induction machine is controlled instantaneously. For drive. In Induction Motor this can be easily achieved by means this the flux regulator is incorporated in the control loop of the of vector Control/field orientation control methodology [6]. induction machine. For small flux and rapid variation of speed it And hence Field orientation control of an Induction Motor is is difficult to obtained maximum torque. And for the high flux widely used control strategy in the industry due to its high regulation of current is difficult because of voltage deficiency. A reliability [1]-[3]. In Field Orientation Control or Vector proportional and integral (PI) regulator solves these problems. For the reasonable performance of the flux regulation the control, which is a variable frequency drive, a resultant vector bandwidth of the current regulator is high compared to that of of magnetic flux and torque realizes stator current and voltages. the flux regulator. PI regulator, the transfer function of the Using Vector control we can achieve the independent control closed-loop system is set to the first-order low-pass filter. The over flux and torque [4] Different control methodologies have current PI controller’s outputs are the corresponding d and q been studied and implemented along with field orientation axis components of the decoupled stator voltage. The fast control control in last few decades for controlling the induction motor loop executes independent control of stator current components like open loop v/f control, v/f control with slip compensation. and slow control loop executes speed controller. The PI speed V/F control is least preferred control strategy because at low regulator output sets a reference for the torque producing speed, resistive term dominates flux linkage which leads to quadrature axis component of the stator current (풊풔풒) and the PI sudden drop in magnetizing flux up to zero levels. To flourish flux regulator sets a reference for flux producing direct axis the performance of Induction motor at low speed, method used component of the stator current (풊풔풅). is popularly known as voltage boost. It allows torque speed curve to become independent of electrical frequency [5]. Keywords—Internal Model Control(IMC); Vector Control; According to current industry trend, PID controllers are most Induction Motor; Speed regulator; Current regulator preferred controllers in industry. In this paper the Indirect Vector Control method is used for IM control over a wide I. NOMENCLATURE range. The method consists of 3-PI controllers. Tuning a 휔푟 Rotor angular speed multiple PID’s is a tedious job as algorithm presented in [6] for 휔푠 Synchronous speed achieving the maximum torque is rather complex, requiring the 푇퐿 Load Torque tuning of several PI regulators (two PI regulators are used for the current regulation, another one for the speed regulation). 푅푠, 푅푟 Resistance of stator and rotor windings While tuning multi-loop PID’s, Inner loop must be faster as 퐿푠, 퐿푟 Self-inductance of stator and rotor windings compared to outer loop. Most of the time for PID tuning trial 퐿푚 Mutual inductance 푃 Number of pole pairs and error method is used. But its very time consuming. This 푝 makes difficult to obtain an optimal controller gains to get 푉푑푠 Direct-axis stator voltage component excellent control over wide speed and torque range. In this 푉푞푠 Quadrature axis voltage component paper the formula for PID gain calculation is derived. The 푖푠 Space phasor of stator current PID’s are tuned and model is simulated on Real Time simulator 푖푟 Space phasor of rotor current OPAL-RT (OP4500). The field-oriented control utilizes the 푖푑푠 Direct axis stator current component stator current components as control variables. The d- 푖푞푠 Quadrature axis rotor current component component of the stator current acts on the rotor flux, whereas the q-component is proportional to the motor torque as the IJERTV4IS060906 www.ijert.org 817 (This work is licensed under a Creative Commons Attribution 4.0 International License.) International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 4 Issue 06, June-2015 control of the motor flux is obtained indirectly by controlling Adjusting the slip angular frequency indirectly controls the the motor currents. position of the rotor flux. Using this process, the stator current is decomposed to the torque and flux component. III. INDUCTION MOTOR MODELLING Induction motor is modelled in a d-q Stationary reference IV. INDIRECT VECTOR CONTROL frame given by the equations of the fluxes and voltages as Induction machines have been utilized for over a hundred 푑 푉 = 푅 푖 + 휓 − 휔 휓 (1) years. Because of their simplicity, ruggedness, reliability, 푑푠 푠 푑푠 푑푡 푑푠 푠 푞푠 푑 efficiency, low cost, compactness, economical and volume 푉 = 푅 푖 + 휓 − 휔 휓 (2) 푞푠 푠 푞푠 푑푡 푞푠 푠 푑푠 manufacturing advantages. Induction machines with a squirrel 푑 0 = 푅 푖 + 휓 − (휔 − 휔 )휓 (3) cage rotor are the most widely used machines at fixed speed. 푟 푑푟 푑푡 푑푟 푠 푟 푞푟 푑 The dynamic model of an induction machine can be expressed 0 = 푅 푖 + 휓 − (휔 − 휔 )휓 (4) 푟 푞푠 푑푡 푞푟 푠 푟 푑푟 by sixth-order state space matrix. Which consists of stator voltage and frequency as inputs and the outputs can be rotor The rotor flux linkages in the reference frame fixed to the speed, rotor position, electromagnetic torque, stator-rotor flux rotor (휓훼푟 휓훽푟) are related to the rotor flux-linkages linkages, magnetic flux linkages, stator-rotor currents and components expressed in the stationary reference frame (휓푑푟 magnetizing current or a combination of these. Induction 푗휃푟 휓푞푟) by the transformation 푒 . Thus the following equation machine can have different rotor windings viz. a wound rotor holds, (slip ring machine) or a squirrel cage windings. The vector control of an induction machine is possible in both types of ⃗휓⃗⃗⃗ = 휓 + 푗휓 (5) windings. The fundamental part in vector control is to get a 푟 푑푟 푞푟 correct space angle, which is the imperative work. The space angle between field winding and stator direct axis as well as ⃗⃗⃗⃗ 푗휃푟 푗휃푟 휓푟푒 = (휓훼푟 + 푗휓훽푟)푒 (6) magnetic flux and stator direct axis can be directly measured in case of an electrically exited synchronous machine and In matrix form:- permanent magnet synchronous machine but not in case of an Induction machine. Furthermore in case of the converter-fed 휓 푐표푠휃 −푠푖푛휃 휓 [ 푑푟] = [ 푟 푟] [ 훼푟] (7) induction machine as there is no external excitation both 휓푞푟 푠푖푛휃푟 푐표푠휃푟 휓훽푟 reactive (excitation) and active (torque producing) currents must simultaneously exist in the stator winding. It has been 휓푑푠 = 퐿푠푖푑푠 + 퐿푚푖푑푟 proved that in special reference frame fixed to magnetizing 휓푞푠 = 퐿푠푖푞푠 + 퐿푚푖푞푟 and stator or rotor flux linkages space phasor, the expression 휓푑푟 = 퐿푟푖푑푟 + 퐿푚푖푑푠 for the electromagnetic torque of the smooth air gap machine 휓푞푟 = 퐿푟푖푞푟 + 퐿푚푖푞푠 is similar to that of separately excited D.C. machine. This recommends that torque and speed control of an induction Based on rotor flux linkages and stator current, the torque is machine can achieve by decoupled control of flux and torque expressed as: producing component of stator currents, which is similar to the field and armature currents in separately excited D.C. 퐿푚 machine. The stator currents can be separated into flux and 푇푒 = 푃푝 (푖푞푠휓푑푟 − 푖푑푠휓푞푟) (8) 퐿푟 torque producing component by utilizing transformations In case of an induction machine rotor flux oriented control is From the field orientation condition i. e. 휓푞푟 = 0 torque usually employed, the modulus and space angle of the rotor equation is written as: flux linkages space phasor are obtained by utilizing the measured stator currents and the rotor speed [8]. As shown in 퐿푚 푇푒 = 푃푝 (푖푞푠휓푑푟) (9) Fig 1 number of PI’s are involved in precise control of an 퐿푟 induction motor. In such case trial and error method of PI The slip angular frequency is represented in terms of rotor tuning is not useful in addition to this tuning by Ziegler flux linkage and q-axis current as: Nichols method is also not useful as the to get the transfer function of such interconnected PI system is not that simple. 푅푟푖푞푟 푅푟 퐿푚 In next section the more useful and easier method of PI tuning 휔푠 − 휔푟 = 휔푠푙 = − = 푖푞푠 (10) 휓푑푟 휓푑푟 퐿푟 is discussed. Under the condition of the constant rotor flux linkages, instantaneous torque of the induction machine is directly proportional to the q-axis stator current.
Load more

Recommended publications
  • Adaptive Digital PID Control of First‐Order‐Lag‐Plus‐Dead‐Time Dynamics with Sensor, Actuator, and Feedback Nonlineari
    Received: 15 May 2019 Revised: 26 September 2019 Accepted: 1 October 2019 DOI: 10.1002/adc2.20 ORIGINAL ARTICLE Adaptive digital PID control of first-order-lag-plus-dead-time dynamics with sensor, actuator, and feedback nonlinearities Mohammadreza Kamaldar1 Syed Aseem Ul Islam1 Sneha Sanjeevini1 Ankit Goel1 Jesse B. Hoagg2 Dennis S. Bernstein1 1Department of Aerospace Engineering, University of Michigan, Ann Arbor, Abstract Michigan Proportional-integral-derivative (PID) control is one of the most widely used 2 Department of Mechanical Engineering, feedback control strategies because of its ability to follow step commands University of Kentucky, Lexington, Kentucky and reject constant disturbances with zero asymptotic error, as well as the ease of tuning. This paper presents an adaptive digital PID controller for Correspondence Dennis S. Bernstein, Department of sampled-data systems with sensor, actuator, and feedback nonlinearities. The Aerospace Engineering, 1320 Beal linear continuous-time dynamics are assumed to be first-order lag with dead Avenue, University of Michigan, Ann time (ie, delay). The plant gain is assumed to have known sign but unknown Arbor, MI 48109. Email: [email protected] magnitude, and the dead time is assumed to be unknown. The sensor and actu- ator nonlinearities are assumed to be monotonic, with known trend but are Funding information AFOSR under DDDAS, Grant/Award otherwise unknown, and the feedback nonlinearity is assumed to be monotonic, Number: FA9550-18-1-0171; ONR, but is otherwise unknown. A numerical investigation is presented to support a Grant/Award Number: N00014-18-1-2211 simulation-based conjecture, which concerns closed-loop stability and perfor- and N00014-19-1-2273 mance.
    [Show full text]
  • Metaheuristic Tuning of Linear and Nonlinear PID Controllers to Nonlinear Mass Spring Damper System
    International Journal of Applied Engineering Research ISSN 0973-4562 Volume 12, Number 10 (2017) pp. 2320-2328 © Research India Publications. http://www.ripublication.com Metaheuristic Tuning of Linear and Nonlinear PID Controllers to Nonlinear Mass Spring Damper System Sudarshan K. Valluru1 and Madhusudan Singh2 Department of Electrical Engineering, Delhi Technological University Bawana Road, Delhi-110042, India. 1ORCID: 0000-0002-8348-0016 Abstract difficulties such as monotonous tuning via priori knowledge into the controller. Currently several metaheuristic algorithms such This paper makes an evaluation of the metaheuristic algorithms as genetic algorithms (GA) and particle swarm optimization namely multi-objective genetic algorithm (MOGA) and (PSO) etc. have been proposed to estimate the optimised tuning adaptive particle swarm optimisation (APSO) algorithms to gains of PID controllers[4] for linear systems. But these basic determine optimal gain parameters of linear and nonlinear PID variants of GA and PSO algorithms have the tendency to controllers. The optimal gain parameters, such as Kp, Ki and Kd premature convergence for multi-dimensional systems[5]. This are applied for controlling of laboratory scaled benchmarked has been the motivation in the direction to use improved variants nonlinear mass-spring-damper (NMSD) system in order to of these algorithms, such as MOGA and APSO techniques to gauge their efficacy. A series of experimental simulation compute L-PID and NL-PID gains according to the bench scaled results reveals that the performance of the APSO tuned NMSD system, such that premature convergence and tedious tunings are diminished. In recent past several bio-inspired nonlinear PID controller is better in the aspects of system metaheuristics such as GA and PSO used for tuning of overshoot, steady state error, settling time of the trajectory for conventional PI and PID controllers [6]–[10].
    [Show full text]
  • Application of the Pid Control to the Programmable Logic Controller Course
    AC 2009-955: APPLICATION OF THE PID CONTROL TO THE PROGRAMMABLE LOGIC CONTROLLER COURSE Shiyoung Lee, Pennsylvania State University, Berks Page 14.224.1 Page © American Society for Engineering Education, 2009 Application of the PID Control to the Programmable Logic Controller Course Abstract The proportional, integral, and derivative (PID) control is the most widely used control technique in the automation industries. The importance of the PID control is emphasized in various automatic control courses. This topic could easily be incorporated into the programmable logic controller (PLC) course with both static and dynamic teaching components. In this paper, the integration of the PID function into the PLC course is described. The proposed new PID teaching components consist of an oven heater and a light dimming control as the static applications, and the closed-loop velocity control of a permanent magnet DC motor (PMDCM) as the dynamic application. The RSLogix500 ladder logic programming software from Rockwell Automation has the PID function. After the theoretical background of the PID control is discussed, the PID function of the SLC500 will be introduced. The first exercise is the pure mathematical implementation of the PID control algorithm using only mathematical PLC instructions. The Excel spreadsheet is used to verify the mathematical PID control algorithm. This will give more insight into the PID control. Following this, the class completes the exercise with the PID instruction in RSLogix500. Both methods will be compared in terms of speed, complexity, and accuracy. The laboratory assignments in controlling the oven heater temperature and dimming the lamp are given to the students so that they experience the effectiveness of the PID control.
    [Show full text]
  • A Comparison Between a Traditional PID Controller and an Artificial Neural Network Controller in Manipulating a Robotic Arm
    EXAMENSARBETE INOM TEKNIK, GRUNDNIVÅ, 15 HP STOCKHOLM, SVERIGE 2019 A comparison between a traditional PID controller and an Artificial Neural Network controller in manipulating a robotic arm En jämförelse mellan en traditionell PID- styrenhet och en Artificiell Neural Nätverksstyrenhet för att styra en robotarm JOSEPH ARISS SALIM RABAT KTH SKOLAN FÖR ELEKTROTEKNIK OCH DATAVETENSKAP Introduction A comparison between a traditional PID controller and an Artificial Neural Network controller in manipulating a robotic arm En jämförelse mellan en traditionell PID-styrenhet och en Artificiell Neural Nätverksstyrenhet för att styra en robotarm Joseph Ariss Salim Rabat 2019-06-06 Bachelor’s Thesis Examiner Örjan Ekeberg Academic adviser Jörg Conradt KTH Royal Institute of Technology School of Electrical Engineering and Computer Science (EECS) SE-100 44 Stockholm, Sweden Abstract Robotic and control industry implements different control technique to control the movement and the position of a robotic arm. PID controllers are the most used controllers in the robotics and control industry because of its simplicity and easy implementation. However, PIDs’ performance suffers under noisy environments. In this research, a controller based on Artificial Neural Networks (ANN) called the model reference controller is examined to replace traditional PID controllers to control the position of a robotic arm in a noisy environment. Simulations and implementations of both controllers were carried out in MATLAB. The training of the ANN was also done in MATLAB using the Supervised Learning (SL) model and Levenberg-Marquardt backpropagation algorithm. Results shows that the ANN implementation performs better than traditional PID controllers in noisy environments. Keywords: Artificial Intelligence, Artificial Neural Network, Control System, PID Controller, Model Reference Controller, Robot arm 1 Introduction Sammanfattning Robot- och kontrollindustrin implementerar olika kontrolltekniker för att styra rörelsen och placeringen av en robotarm.
    [Show full text]
  • Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems
    energies Article Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems Yuqi Fan, Junpeng Shao, Guitao Sun and Xuan Shao * Key Laboratory of Advanced Manufacturing and Intelligent Technology, Ministry of Education, School of Mechanical and Power Engineering, Harbin University of Science and Technology, Harbin 150080, China; [email protected] (Y.F.); [email protected] (J.S.); [email protected] (G.S.) * Correspondence: [email protected] Received: 26 November 2019; Accepted: 15 January 2020; Published: 17 January 2020 Abstract: To improve the control ability of proportional–integral–derivative (PID) controllers and increase the stability of force actuator systems, this paper introduces a PID controller based on the self-growing lévy-flight salp swarm algorithm (SG-LSSA) in the force actuator system. First, the force actuator system model was built, and the transfer function model was obtained by the identification of system parameters identifying. Second, the SG-LSSA was proposed and used to test ten benchmark functions. Then, SG-LSSA-PID, whose parameters were tuned by SG-LSSA, was applied to the electro-hydraulic force actuator system to suppress interference signals. Finally, the temporal response characteristic and the frequency response characteristic were studied and compared with different algorithms. Ten benchmark function experiments indicate that SG-LSSA has a superior convergence speed and perfect optimization capability. The system performance results demonstrate that the electro-hydraulic force actuator system utilized the SG-LSSA-PID controller has a remarkable capability to maintain the stability and robustness under unknown interference signals. Keywords: salp swarm algorithm; PID controller; control strategy 1.
    [Show full text]
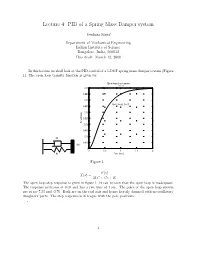
  • Lecture 4: PID of a Spring Mass Damper System
    Lecture 4: PID of a Spring Mass Damper system Venkata Sonti∗ Department of Mechanical Engineering Indian Institute of Science Bangalore, India, 560012 This draft: March 12, 2008 In this lecture we shall look at the PID control of a 1-DOF spring mass damper system (Figure 1). The open loop transfer function is given by: Open loop step response From: U(1) 0.05 0.045 0.04 M=1, K=20, C=10 0.035 0.03 0.025 Amplitude 0.02 0.015 0.01 C 0.005 M 0 0 0.5 1 1.5 2 K Time (sec.) Figure 1: F (s) X(s)= Ms2 + Cs + K The open loop step response is given in figure 1. It can be seen that the open loop is inadequate. The response saturates at 0.05 and has a rise time of 1 sec. The poles of the open loop system are at s=-7.23 and -2.76. Both are on the real axis and hence heavily damped with no oscillatory imaginary parts. The step response is in league with the pole positions. ∗ 1 1 Proportional Controller We should first reduce the steady state error, for which we look at the proportional controller. The block diagram for the proportional controller is given in figure 2. Proportional controller step response 1.4 1.2 Kp=300, M=1, K=20, C=10 1 0.8 0.6 Amplitude 0.4 r(t) 1 + Kp R(s) - s2 +10s+20 0.2 0 0 0.2 0.4 0.6 0.8 1 1.2 Time (sec.) Figure 2: Block diagram for proportional controller.
    [Show full text]
  • Design and Analysis of Speed Control Using Hybrid PID-Fuzzy Controller for Induction Motors
    Western Michigan University ScholarWorks at WMU Master's Theses Graduate College 6-2015 Design and Analysis of Speed Control Using Hybrid PID-Fuzzy Controller for Induction Motors Ahmed Fattah Follow this and additional works at: https://scholarworks.wmich.edu/masters_theses Part of the Automotive Engineering Commons, and the Electrical and Computer Engineering Commons Recommended Citation Fattah, Ahmed, "Design and Analysis of Speed Control Using Hybrid PID-Fuzzy Controller for Induction Motors" (2015). Master's Theses. 595. https://scholarworks.wmich.edu/masters_theses/595 This Masters Thesis-Open Access is brought to you for free and open access by the Graduate College at ScholarWorks at WMU. It has been accepted for inclusion in Master's Theses by an authorized administrator of ScholarWorks at WMU. For more information, please contact [email protected]. DESIGN AND ANALYSIS OF SPEED CONTROL USING HYBRID PID-FUZZY CONTROLLER FOR INDUCTION MOTORS by Ahmed Fattah A thesis submitted to the Graduate College in partial fulfillment of the requirements for the degree of Master of Science in Engineering (Electrical) Electrical and Computer Engineering Western Michigan University June 2015 Thesis Committee: Ikhlas Abdel-Qader, Ph.D., Chair Johnson Asumadu, Ph.D. Abdolazim Houshyar, Ph.D. DESIGN AND ANALYSIS OF SPEED CONTROL USING HYBRID PID-FUZZY CONTROLLER FOR INDUCTION MOTORS Ahmed Jumaah Fattah, M.S.E. Western Michigan University, 2015 This thesis presents a hybrid PID-Fuzzy control system for the speed control of a three-phase squirrel cage induction motor. The proposed method incorporates fuzzy logic and conventional controllers with utilization of vector control technique. This method combines the advantages of fuzzy logic controller and conventional controllers to improve the speed response of the induction motor.
    [Show full text]
  • 8. Feedback Control Systems
    feedback control - 8.1 8. FEEDBACK CONTROL SYSTEMS Topics: • Transfer functions, block diagrams and simplification • Feedback controllers • Control system design Objectives: • To be able to represent a control system with block diagrams. • To be able to select controller parameters to meet design objectives. 8.1 INTRODUCTION Every engineered component has some function. A function can be described as a transformation of inputs to outputs. For example it could be an amplifier that accepts a sig- nal from a sensor and amplifies it. Or, consider a mechanical gear box with an input and output shaft. A manual transmission has an input shaft from the motor and from the shifter. When analyzing systems we will often use transfer functions that describe a sys- tem as a ratio of output to input. 8.2 TRANSFER FUNCTIONS Transfer functions are used for equations with one input and one output variable. An example of a transfer function is shown below in Figure 8.1. The general form calls for output over input on the left hand side. The right hand side is comprised of constants and the ’D’ operator. In the example ’x’ is the output, while ’F’ is the input. The general form An example output x 4 + D ----------------- = fD() --- = --------------------------------- input F D2 ++4D 16 Figure 8.1 A transfer function example feedback control - 8.2 If both sides of the example were inverted then the output would become ’F’, and the input ’x’. This ability to invert a transfer function is called reversibility. In reality many systems are not reversible. There is a direct relationship between transfer functions and differential equations.
    [Show full text]
  • Feedback Systems
    Feedback Systems An Introduction for Scientists and Engineers SECOND EDITION Karl Johan Astr¨om˚ Richard M. Murray Version v3.0j (2019-08-17) This is the electronic edition of Feedback Systems and is available from http://fbsbook.org. Hardcover editions may be purchased from Princeton University Press, http://press.princeton.edu/titles/8701.html. This manuscript is for personal use only and may not be reproduced, in whole or in part, without written consent from the publisher (see http://press.princeton.edu/permissions.html). i Chapter Eleven PID Control Based on a survey of over eleven thousand controllers in the refining, chem- icals and pulp and paper industries, 97% of regulatory controllers utilize a PID feedback control algorithm. L. Desborough and R. Miller, 2002 [DM02a]. Proportional-integral-derivative (PID) control is by far the most common way of using feedback in engineering systems. In this chapter we will present the basic properties of PID control and the methods for choosing the parameters of the controllers. We also analyze the effects of actuator saturation, an important feature of many feedback systems, and describe methods for compensating for it. Finally, we will discuss the implementation of PID controllers as an example of how to implement feedback control systems using analog or digital computation. 11.1 BASIC CONTROL FUNCTIONS The PID controller was introduced in Section 1.6, where Figure 1.15 illustrates that control action is composed of three terms: the proportional term (P), which depends on the present error; the integral term (I), which depends on past errors; and the derivative term (D), which depends on anticipated future errors.
    [Show full text]
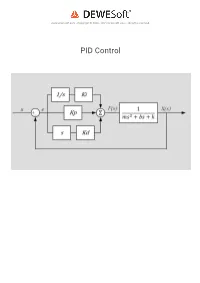
  • PID Control Introduction to Process Control
    www.dewesoft.com - Copyright © 2000 - 2021 Dewesoft d.o.o., all rights reserved. PID Control Introduction to Process Control A controller is a mechanism that controls the output of a system by adjusting its control input. A feedback controller continuously measures the output, compares it to the desired output (the setpoint), and adjusts the input depending on the calculated error. A PID controller is the most common type of feedback controller. It adjusts the control variable depending on the present error (P - proportional control), the accumulated error in the past (I - integral control), and the predicted future error (D - derivative control). A block diagram of a PID controller can be seen in the figure below. The Plant/Process block represents the system to which we apply the input ( u) and it returns the output (y). A car is a system to which we apply a steering wheel angle command as an input and it responds with a change of direction as an output. The characteristics of the car such as its weight, center of gravity position, suspension geometry, and tires will dene the direction change for a given change in steering wheel angle. If a controller is implemented, the input u is calculated as shown in the diagram by summing the proportional, integral, and derivative terms. The terms are obtained by multiplying the error, the integral of the error and the derivative of the error with P, I and D gains respectively. 1 What is the role of the Controller Gains (Kp, Kd, Ki)? Let's look at an example to get a better feeling for the practical implementation of a PID controller.
    [Show full text]
  • Basics of Control Based on Slides by Benjamin Kuipers
    Basics of Control Based on slides by Benjamin Kuipers How can an information system (like a micro-CONTROLLER, a fly-ball governor, or your brain) control the physical world? Examples: Thermostat You, walking down the street without falling over A robot trying to keep a joint at a particular angle A blimp trying to maintain a particular heading despite air movement in the room A robot finger trying to maintain a particular distance from an object CSE 466 Control 1 A controller Controller is trying to balance sensor values on 4 sensors CSE 466 Control 2 Controlling a Simple System “is a fn of” Change in state State Consider a simple system: xFxu (,) Action Scalar variables x and u, not vectors x and u. Assume effect of motor command u: F 0 u The setpoint xset is the desired value. The controller responds to error: e = x xset The goal is to set u to reach e = 0. Joint angle controller example State : joint angle Action : motor command causes to change: 0 Sensor : joint angle encoder Set point : a target joint angle (or vector of angles) Linear restoring force / Quadratic error function spring like behavior 2 Spring Force F kx Spring Energy E1 2( x x0 ) CSE 466 Control 4 The intuition behind control Use action u to push back toward error e = 0 What does pushing back do? Position vs velocity versus acceleration control How much should we push back? What does the magnitude of u depend on? Velocity or acceleration control? Velocity: xxu ()xF (, ) () u x (x) Acceleration: xv xxu F(, ) vu x x v vxu Laws of Motion in Physics Newton’s Law: F=ma or a=F/m.
    [Show full text]
  • 07-PID Controller.Pdf
    PID Controller 1. Introduction A proportional-integral-derivative controller (PID controller) is a control loop feedback mechanism (controller) widely used in industrial control systems. A PID controller calculates an error value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error by adjusting the process through use of a manipulated variable. The PID controller algorithm involves three separate constant parameters, and is accordingly sometimes called three-term control: the proportional, the integral and derivative values, denoted P, I, and D. Simply put, these values can be interpreted in terms of time: P depends on the present error, I on the accumulation of past errors, and D is a prediction of future errors, based on current rate of change. The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve, a damper, or the power supplied to a heating element. In the absence of knowledge of the underlying process, a PID controller has historically been considered to be the most useful controller. By tuning the three parameters in the PID controller algorithm, the controller can provide control action designed for specific process requirements. The response of the controller can be described in terms of the responsiveness of the controller to an error, the degree to which the controller overshoots the setpoint, and the degree of system oscillation. Note that the use of the PID algorithm for control does not guarantee optimal control of the system or system stability.
    [Show full text]