DOCSLIB.ORG

Higher Inductive Types (Hits) Are a New Type Former!

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Higher Inductive Types (Hits) Are a New Type Former! Git as a HIT Dan Licata Wesleyan University 1 1 Darcs Git as a HIT Dan Licata Wesleyan University 1 1 HITs 2 Generator for 2 equality of equality HITs Homotopy Type Theory is an extension of Agda/Coq based on connections with homotopy theory [Hofmann&Streicher,Awodey&Warren,Voevodsky,Lumsdaine,Garner&van den Berg] 2 Generator for 2 equality of equality HITs Homotopy Type Theory is an extension of Agda/Coq based on connections with homotopy theory [Hofmann&Streicher,Awodey&Warren,Voevodsky,Lumsdaine,Garner&van den Berg] Higher inductive types (HITs) are a new type former! 2 Generator for 2 equality of equality HITs Homotopy Type Theory is an extension of Agda/Coq based on connections with homotopy theory [Hofmann&Streicher,Awodey&Warren,Voevodsky,Lumsdaine,Garner&van den Berg] Higher inductive types (HITs) are a new type former! They were originally invented[Lumsdaine,Shulman,…] to model basic spaces (circle, spheres, the torus, …) and constructions in homotopy theory 2 Generator for 2 equality of equality HITs Homotopy Type Theory is an extension of Agda/Coq based on connections with homotopy theory [Hofmann&Streicher,Awodey&Warren,Voevodsky,Lumsdaine,Garner&van den Berg] Higher inductive types (HITs) are a new type former! They were originally invented[Lumsdaine,Shulman,…] to model basic spaces (circle, spheres, the torus, …) and constructions in homotopy theory But they have many other applications, including some programming ones! 2 Generator for 2 equality of equality Patches Patch a a 2c2 diff b d = < b c c --- > d 3 3 id a a b b c c 4 4 id a a b b c c a p a q a b d d c c e 4 4 id a a b b c c q o p a p a q a b d d c c e 4 4 id p a a a a b b b d c c c c q o p a p a q a b d d c c e 4 4 id p a a a a b b b d c c c c !p q o p a p a q a b d d c c e 4 4 id p a a a a b b b d c c c c !p q o p undo/rollback a p a q a b d d c c e 4 4 id p a a a a b b b d c c c c !p q o p undo/rollback a p a q a b d d c c e [Yorgey,Jacobson,…] 4 4 Simple Setup a u s s o i s a ↔ b at 0 a u s b u s a ↔ b at 0 5 5 Simple Setup “Repository” is a char vector of fixed length n a u s s o i s Basic patch is a ↔ b at i where i<n a ↔ b at 0 a u s b u s a ↔ b at 0 5 5 Domain-Specific Language 6 6 Domain-Specific Language 7 7 Domain-Specific Language swapat a b i v permutes a and b at position i in v 7 7 Domain-Specific Language Spec: ∀ p. interp p is a bijection: ∀ v. g (f v) = v where (f,g)=interp p ∀ v. f (g v) = v 8 8 Domain-Specific Language undo really un-does Spec: ∀ p. interp p is a bijection: ∀ v. g (f v) = v where (f,g)=interp p ∀ v. f (g v) = v 8 8 Domain-Specific Language undo really un-does Spec: ∀ p. interp p is a bijection: ∀ v. g (f v) = v where (f,g)=interp p ∀ v. f (g v) = v Can package this as: 8 8 Merging a p b q c a a d b c e 9 9 Merging a p b q c a a d b c e q’ a p’ d e 9 9 Merging p=b↔d at 1 a q=c↔e at 2 p b q c a a d b c e q’ a p’ d e 9 9 Merging p=b↔d at 1 a q=c↔e at 2 p b q c a a d b c e q’ a p’ d p’=p e q’=q 9 9 Merging p=b↔d at 1 a q=c↔e at 2 p b q c a a d b c = e q’ a p’ d p’=p e q’=q 9 9 Merging merge : (p q : Patch) ! "q’,p’:Patch. Maybe(q’ o p = p’ o q) 10 10 Merging merge : (p q : Patch) ! "q’,p’:Patch. Maybe(q’ o p = p’ o q) When are two patches equal? 10 10 Patch Equality (a↔b at i)o(c↔d at j) = (c↔d at j)o(a↔b at i) if i#j 11 11 Patch Equality (a↔b at i)o(c↔d at j) = (c↔d at j)o(a↔b at i) if i#j (a↔a at i) = id !(a↔b at i) = (a↔b at i) (a↔b at i) = (b↔a at i) 11 11 Patch Equality Basic Axioms: (a↔b at i)o(c↔d at j) = (c↔d at j)o(a↔b at i) if i#j (a↔a at i) = id !(a↔b at i) = (a↔b at i) (a↔b at i) = (b↔a at i) 11 11 Patch Equality Basic axioms: (a↔b at i)o(c↔d at j) =(c↔d at j)o(a↔b at i) 12 12 Patch Equality Basic axioms: Group laws: (a↔b at i)o(c↔d at j) id o p = p = p o id =(c↔d at j)o(a↔b at i) po(qor) = (poq)or !p o p = id = p o !p 12 12 Patch Equality Basic axioms: Group laws: (a↔b at i)o(c↔d at j) id o p = p = p o id =(c↔d at j)o(a↔b at i) po(qor) = (poq)or !p o p = id = p o !p Congruence: p=p !p = !p’ if p = p’ p=q if q=p p o q = p’ o q’ if p=r if p=q and q=r p = p’ and q = q’ 12 12 Patch as Quotient Type Elements: Equality: (a↔b at i)o(c↔d at j)~ (c↔d at j)o(a↔b at i) ... id o p ~ p ~ p o id po(qor) ~ (poq)or !p o p ~ id ~ p o !p p~p p~q if q~p p~r if p~q and q~r !p ~ !p’ if p ~ p’ p o q ~ p’ o q’ if p ~ p’ and q ~ q’ 13 13 Patch as Quotient Type Elements: Quotient Type: Patch := Patch’/~ Equality: (a↔b at i)o(c↔d at j)~ (c↔d at j)o(a↔b at i) ... id o p ~ p ~ p o id po(qor) ~ (poq)or !p o p ~ id ~ p o !p p~p p~q if q~p p~r if p~q and q~r !p ~ !p’ if p ~ p’ p o q ~ p’ o q’ if p ~ p’ and q ~ q’ 13 13 Patch as Quotient Type Elements: Quotient Type: Patch := Patch’/~ Equality: Elimination rule: (a↔b at i)o(c↔d at j)~ (c↔d at j)o(a↔b at i) ... id o p ~ p ~ p o id define on Patch’ as before, po(qor) ~ (poq)or then prove p ~ q implies !p o p ~ id ~ p o !p p~p interp p = interp q p~q if q~p for all 14+ rules for ~ p~r if p~q and q~r !p ~ !p’ if p ~ p’ p o q ~ p’ o q’ if p ~ p’ and q ~ q’ 13 13 Patches as a HIT 1.How do you define Patch using a higher inductive type? 2.What is the elimination rule? 3.How do you use the elim. rule to define interp? 14 14 Patches as a HIT 1.How do you define Patch using a higher inductive type? 2.What is the elimination rule? 3.How do you use the elim. rule to define interp? 15 15 Higher Inductive Type 16 Generator for 16 equality of equality Higher Inductive Type Type freely generated by constructors for elements, equalities, equalities between equalities, … 16 Generator for 16 equality of equality Higher Inductive Type Type freely generated by constructors for elements, equalities, equalities between equalities, … RepoDesc : Type 16 Generator for 16 equality of equality Higher Inductive Type Type freely generated by constructors for elements, equalities, equalities between equalities, … RepoDesc : Type vec : RepoDesc generator for element 16 Generator for 16 equality of equality Higher Inductive Type Type freely generated by constructors for elements, equalities, equalities between equalities, … RepoDesc : Type vec : RepoDesc generator for element (a↔b at i) : vec = vec generator for equality 16 Generator for 16 equality of equality Higher Inductive Type Type freely generated by constructors for elements, equalities, equalities between equalities, … RepoDesc : Type proof-relevant! vec : RepoDesc generator for element (a↔b at i) : vec = vec generator for equality 16 Generator for 16 equality of equality Higher Inductive Type Type freely generated by constructors for elements, equalities, equalities between equalities, … RepoDesc : Type proof-relevant! vec : RepoDesc generator for element (a↔b at i) : vec = vec generator for equality commute: generator for equality (a↔b at i)o(c↔d at j) between equalities =(c↔d at j)o(a↔b at i) 16 Generator for 16 equality of equality Type: Patch Elements: Equality: (a↔b at i)o(c↔d at j)= (c↔d at j)o(a↔b at i) ..
Load more

Recommended publications
  • Generating Commit Messages from Git Diffs
    Generating Commit Messages from Git Diffs Sven van Hal Mathieu Post Kasper Wendel Delft University of Technology Delft University of Technology Delft University of Technology [email protected] [email protected] [email protected] ABSTRACT be exploited by machine learning. The hypothesis is that methods Commit messages aid developers in their understanding of a con- based on machine learning, given enough training data, are able tinuously evolving codebase. However, developers not always doc- to extract more contextual information and latent factors about ument code changes properly. Automatically generating commit the why of a change. Furthermore, Allamanis et al. [1] state that messages would relieve this burden on developers. source code is “a form of human communication [and] has similar Recently, a number of different works have demonstrated the statistical properties to natural language corpora”. Following the feasibility of using methods from neural machine translation to success of (deep) machine learning in the field of natural language generate commit messages. This work aims to reproduce a promi- processing, neural networks seem promising for automated commit nent research paper in this field, as well as attempt to improve upon message generation as well. their results by proposing a novel preprocessing technique. Jiang et al. [12] have demonstrated that generating commit mes- A reproduction of the reference neural machine translation sages with neural networks is feasible. This work aims to reproduce model was able to achieve slightly better results on the same dataset. the results from [12] on the same and a different dataset. Addition- When applying more rigorous preprocessing, however, the per- ally, efforts are made to improve upon these results by applying a formance dropped significantly.
    [Show full text]
  • Introduction to Version Control with Git
    Warwick Research Software Engineering Introduction to Version Control with Git H. Ratcliffe and C.S. Brady Senior Research Software Engineers \The Angry Penguin", used under creative commons licence from Swantje Hess and Jannis Pohlmann. March 12, 2018 Contents 1 About these Notes1 2 Introduction to Version Control2 3 Basic Version Control with Git4 4 Releases and Versioning 11 Glossary 14 1 About these Notes These notes were written by H Ratcliffe and C S Brady, both Senior Research Software Engineers in the Scientific Computing Research Technology Platform at the University of Warwick for a series of Workshops first run in December 2017 at the University of Warwick. This document contains notes for a half-day session on version control, an essential part of the life of a software developer. This work, except where otherwise noted, is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International Li- cense. To view a copy of this license, visit http://creativecommons.org/ licenses/by-nc-nd/4.0/. The notes may redistributed freely with attribution, but may not be used for commercial purposes nor altered or modified. The Angry Penguin and other reproduced material, is clearly marked in the text and is not included in this declaration. The notes were typeset in LATEXby H Ratcliffe. Errors can be reported to [email protected] 1.1 Other Useful Information Throughout these notes, we present snippets of code and pseudocode, in particular snippets of commands for shell, make, or git. These often contain parts which you should substitute with the relevant text you want to use.
    [Show full text]
  • Efficient Algorithms for Comparing, Storing, and Sharing
    EFFICIENT ALGORITHMS FOR COMPARING, STORING, AND SHARING LARGE COLLECTIONS OF EVOLUTIONARY TREES A Dissertation by SUZANNE JUDE MATTHEWS Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY May 2012 Major Subject: Computer Science EFFICIENT ALGORITHMS FOR COMPARING, STORING, AND SHARING LARGE COLLECTIONS OF EVOLUTIONARY TREES A Dissertation by SUZANNE JUDE MATTHEWS Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Approved by: Chair of Committee, Tiffani L. Williams Committee Members, Nancy M. Amato Jennifer L. Welch James B. Woolley Head of Department, Hank W. Walker May 2012 Major Subject: Computer Science iii ABSTRACT Efficient Algorithms for Comparing, Storing, and Sharing Large Collections of Evolutionary Trees. (May 2012) Suzanne Jude Matthews, B.S.; M.S., Rensselaer Polytechnic Institute Chair of Advisory Committee: Dr. Tiffani L. Williams Evolutionary relationships between a group of organisms are commonly summarized in a phylogenetic (or evolutionary) tree. The goal of phylogenetic inference is to infer the best tree structure that represents the relationships between a group of organisms, given a set of observations (e.g. molecular sequences). However, popular heuristics for inferring phylogenies output tens to hundreds of thousands of equally weighted candidate trees. Biologists summarize these trees into a single structure called the consensus tree. The central assumption is that the information discarded has less value than the information retained. But, what if this assumption is not true? In this dissertation, we demonstrate the value of retaining and studying tree collections.
    [Show full text]
  • Homework 0: Account Setup for Course and Cloud FPGA Intro Questions
    Cloud FPGA Homework 0 Fall 2019 Homework 0 Jakub Szefer 2019/10/20 Please follow the three setup sections to create BitBucket git repository, install LATEX tools or setup Overleaf account, and get access to the course's git repository. Once you have these done, answer the questions that follow. Submit your solutions as a single PDF file generated from a template; more information is at end in the Submission Instructions section. Setup BitBucket git Repository This course will use git repositories for code development. Each student should setup a free BitBucket (https://bitbucket.org) account and create a git repository for the course. Please make the repository private and give WRITE access to your instructor ([email protected]). Please send the URL address of the repository to the instructor by e-mail. Make sure there is a README:md file in the repository (access to the repository will be tested by a script that tries to download the README:md from the repository address you share). Also, if you are using a Apple computer, please add :gitignore file which contains one line: :DS Store (to prevent the hidden :DS Store files from accidentally being added to the repository). If you have problems accessing BitBucket git from the command line, please see the Appendix. Setup LATEX and Overleaf Any written work (including this homework's solutions) will be submitted as PDF files generated using LATEX [1] from provided templates. Students can setup a free Overleaf (https://www. overleaf.com) account to edit LATEX files and generate PDFs online; or students can install LATEX tools on their computer.
    [Show full text]
  • Version Control – Agile Workflow with Git/Github
    Version Control – Agile Workflow with Git/GitHub 19/20 November 2019 | Guido Trensch (JSC, SimLab Neuroscience) Content Motivation Version Control Systems (VCS) Understanding Git GitHub (Agile Workflow) References Forschungszentrum Jülich, JSC:SimLab Neuroscience 2 Content Motivation Version Control Systems (VCS) Understanding Git GitHub (Agile Workflow) References Forschungszentrum Jülich, JSC:SimLab Neuroscience 3 Motivation • Version control is one aspect of configuration management (CM). The main CM processes are concerned with: • System building • Preparing software for releases and keeping track of system versions. • Change management • Keeping track of requests for changes, working out the costs and impact. • Release management • Preparing software for releases and keeping track of system versions. • Version control • Keep track of different versions of software components and allow independent development. [Ian Sommerville,“Software Engineering”] Forschungszentrum Jülich, JSC:SimLab Neuroscience 4 Motivation • Keep track of different versions of software components • Identify, store, organize and control revisions and access to it • Essential for the organization of multi-developer projects is independent development • Ensure that changes made by different developers do not interfere with each other • Provide strategies to solve conflicts CONFLICT Alice Bob Forschungszentrum Jülich, JSC:SimLab Neuroscience 5 Content Motivation Version Control Systems (VCS) Understanding Git GitHub (Agile Workflow) References Forschungszentrum Jülich,
    [Show full text]
  • Scaling Git with Bitbucket Data Center
    Scaling Git with Bitbucket Data Center Considerations for large teams switching to Git Contents What is Git, why do I want it, and why is it hard to scale? 01 Scaling Git with Bitbucket Data Center 05 What about compliance? 11 Why choose Bitbucket Data Center? 13 01 What is Git, why do I want it, and why is it hard to scale? So. Your software team is expanding and taking on more high-value projects. That’s great news! The bad news, however, is that your centralized version control system isn’t really cutting it anymore. For growing IT organizations, Some of the key benefits Codebase safety moving to a distributed version control system is now of adopting Git are: Git is designed with maintaining the integrity considered an inevitable shift. This paper outlines some of managed source code as a top priority, using secure algorithms to preserve your code, change of the benefits of Git as a distributed version control system history, and traceability against both accidental and how Bitbucket Data Center can help your company scale and malicious change. Distributed development its Git-powered operations smoothly. Community Distributed development gives each developer a working copy of the full repository history, Git has become the expected version control making development faster by speeding up systems in many circles, and is very popular As software development increases in complexity, and the commit process and reducing developers’ among open source projects. This means its easy development teams become more globalized, centralized interdependence, as well as their dependence to take advantage of third party libraries and on a network connection.
    [Show full text]
  • DVCS Or a New Way to Use Version Control Systems for Freebsd
    Brief history of VCS FreeBSD context & gures Is Arch/baz suited for FreeBSD? Mercurial to the rescue New processes & policies needed Conclusions DVCS or a new way to use Version Control Systems for FreeBSD Ollivier ROBERT <[email protected]> BSDCan 2006 Ottawa, Canada May, 12-13th, 2006 Ollivier ROBERT <[email protected]> DVCS or a new way to use Version Control Systems for FreeBSD Brief history of VCS FreeBSD context & gures Is Arch/baz suited for FreeBSD? Mercurial to the rescue New processes & policies needed Conclusions Agenda 1 Brief history of VCS 2 FreeBSD context & gures 3 Is Arch/baz suited for FreeBSD? 4 Mercurial to the rescue 5 New processes & policies needed 6 Conclusions Ollivier ROBERT <[email protected]> DVCS or a new way to use Version Control Systems for FreeBSD Brief history of VCS FreeBSD context & gures Is Arch/baz suited for FreeBSD? Mercurial to the rescue New processes & policies needed Conclusions The ancestors: SCCS, RCS File-oriented Use a subdirectory to store deltas and metadata Use lock-based architecture Support shared developments through NFS (fragile) SCCS is proprietary (System V), RCS is Open Source a SCCS clone exists: CSSC You can have a central repository with symlinks (RCS) Ollivier ROBERT <[email protected]> DVCS or a new way to use Version Control Systems for FreeBSD Brief history of VCS FreeBSD context & gures Is Arch/baz suited for FreeBSD? Mercurial to the rescue New processes & policies needed Conclusions CVS, the de facto VCS for the free world Initially written as shell wrappers over RCS then rewritten in C Centralised server Easy UI Use sandboxes to avoid locking Simple 3-way merges Can be replicated through CVSup or even rsync Extensive documentation (papers, websites, books) Free software and used everywhere (SourceForge for example) Ollivier ROBERT <[email protected]> DVCS or a new way to use Version Control Systems for FreeBSD Brief history of VCS FreeBSD context & gures Is Arch/baz suited for FreeBSD? Mercurial to the rescue New processes & policies needed Conclusions CVS annoyances and aws BUT..
    [Show full text]
  • Git Basics Git Expertise
    Overview Git basics Git expertise Git A GNU Alternative to Bitkeeper Mohamed Barakat University of Kaiserslautern ITWM Kaiserslautern, January 2010 Mohamed Barakat Git Overview Git basics Git expertise 1 Git basics The Git configuration file Create a Git-repository Using a Git-repository 2 Git expertise Branching Pulling Merging and Cherry-Picking Mohamed Barakat Git Overview The Git configuration file Git basics Create a Git-repository Git expertise Using a Git-repository Overview 1 Git basics The Git configuration file Create a Git-repository Using a Git-repository 2 Git expertise Branching Pulling Merging and Cherry-Picking Mohamed Barakat Git Overview The Git configuration file Git basics Create a Git-repository Git expertise Using a Git-repository Git working copy and Git-repsoitory Git is a distributed SCM Git is a distributed Source Code Management system (SCM), i.e. each Git working copy sits on top of its own local Git repository located in a single top-level subdirectory .git. SVN is in contrast to Git a centralized SCM system, i.e. the SVN-repository is on exactly one server. Git allows you to commit, checkout, reset, etc. without contacting a server! Mohamed Barakat Git Overview The Git configuration file Git basics Create a Git-repository Git expertise Using a Git-repository The configuration file ˜/.gitconfig Create a Git configuration file vi ˜/.gitconfig [svn] authorsfile = .git/info/svn-authors [color] diff = auto status = auto branch = auto [user] name = Firstname Lastname email = [email protected] Mohamed Barakat Git Overview The Git configuration file Git basics Create a Git-repository Git expertise Using a Git-repository Create a Git-repository (quick version) init, add, commit Create a Git-repository in the directory XY: 1 cd XY 2 git init 3 git add .
    [Show full text]
  • INF5750/9750 - Lecture 1 (Part III) Problem Area
    Revision control INF5750/9750 - Lecture 1 (Part III) Problem area ● Software projects with multiple developers need to coordinate and synchronize the source code Approaches to version control ● Work on same computer and take turns coding ○ Nah... ● Send files by e-mail or put them online ○ Lots of manual work ● Put files on a shared disk ○ Files get overwritten or deleted and work is lost, lots of direct coordination ● In short: Error prone and inefficient The preferred solution ● Use a revision control system. RCS - software that allows for multiple developers to work on the same codebase in a coordinated fashion ● History of Revision Control Systems: ○ File versioning tools, e.g. SCCS, RCS ○ Central Style - tree versioning tools. e.g. CVS ○ Central Style 2 - tree versioning tools e.g. SVN ○ Distributed style - tree versioning tools e.g. Bazaar ● Modern DVCS include Git, Mercurial, Bazaar Which system in this course? ● In this course we will be using GIT as the version control system ● We will use the UIO git system, but you can also make git accounts on github.com or bitbucket for your own projects ● DHIS2 uses a different system: Launchpad/Bazaar How it works Working tree: Local copy of the source code Repository: residing on the Central storage of developer’s the source code at computer (a client) a server synchronize synchronize Commit Commit locally Centralized De-centralized The repository Central ● Remembers every change ever written to it (called commits) ● You can have a central or local repository. ○ Central = big server in
    [Show full text]
  • Darcs 2.0.0 (2.0.0 (+ 75 Patches)) Darcs
    Darcs 2.0.0 (2.0.0 (+ 75 patches)) Darcs David Roundy April 23, 2008 2 Contents 1 Introduction 7 1.1 Features . 9 1.2 Switching from CVS . 11 1.3 Switching from arch . 12 2 Building darcs 15 2.1 Prerequisites . 15 2.2 Building on Mac OS X . 16 2.3 Building on Microsoft Windows . 16 2.4 Building from tarball . 16 2.5 Building darcs from the repository . 17 2.6 Building darcs with git . 18 2.7 Submitting patches to darcs . 18 3 Getting started 19 3.1 Creating your repository . 19 3.2 Making changes . 20 3.3 Making your repository visible to others . 20 3.4 Getting changes made to another repository . 21 3.5 Moving patches from one repository to another . 21 3.5.1 All pulls . 21 3.5.2 Send and apply manually . 21 3.5.3 Push . 22 3.5.4 Push —apply-as . 22 3.5.5 Sending signed patches by email . 23 3.6 Reducing disk space usage . 26 3.6.1 Linking between repositories . 26 3.6.2 Alternate formats for the pristine tree . 26 4 Configuring darcs 29 4.1 prefs . 29 4.2 Environment variables . 32 4.3 General-purpose variables . 33 4.4 Remote repositories . 34 3 4 CONTENTS 4.5 Highlighted output . 36 4.6 Character escaping and non-ASCII character encodings . 36 5 Best practices 39 5.1 Introduction . 39 5.2 Creating patches . 39 5.2.1 Changes . 40 5.2.2 Keeping or discarding changes . 40 5.2.3 Unrecording changes .
    [Show full text]
  • Hg Mercurial Cheat Sheet Serge Y
    Hg Mercurial Cheat Sheet Serge Y. Stroobandt Copyright 2013–2020, licensed under Creative Commons BY-NC-SA #This page is work in progress! Much of the explanatory text still needs to be written. Nonetheless, the basic outline of this page may already be useful and this is why I am sharing it. In the mean time, please, bare with me and check back for updates. Distributed revision control Why I went with Mercurial • Python, Mozilla, Java, Vim • Mercurial has been better supported under Windows. • Mercurial also offers named branches Emil Sit: • August 2008: Mercurial offers a comfortable command-line experience, learning Git can be a bit daunting • December 2011: Git has three “philosophical” distinctions in its favour, as well as more attention to detail Lowest common denominator It is more important that people start using dis- tributed revision control instead of nothing at all. The Pro Git book is available online. Collaboration styles • Mercurial working practices • Collaborating with other people Use SSH shorthand 1 Installation $ sudo apt-get update $ sudo apt-get install mercurial mercurial-git meld Configuration Local system-wide configuration $ nano .bashrc export NAME="John Doe" export EMAIL="[email protected]" $ source .bashrc ~/.hgrc on a client user@client $ nano ~/.hgrc [ui] username = user@client editor = nano merge = meld ssh = ssh -C [extensions] convert = graphlog = mq = progress = strip = 2 ~/.hgrc on the server user@server $ nano ~/.hgrc [ui] username = user@server editor = nano merge = meld ssh = ssh -C [extensions] convert = graphlog = mq = progress = strip = [hooks] changegroup = hg update >&2 Initiating One starts with initiate a new repository.
    [Show full text]
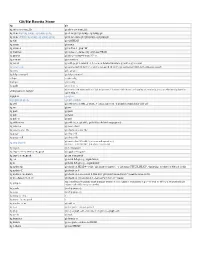
  • Git/Hg Rosetta Stone
    Git/Hg Rosetta Stone hg git hg cat -r rev some_file git show rev:some_file hg clone http://hg.sympy.org/sympy-git.hg git clone git://git.sympy.org/sympy.git hg clone -U http://hg.sympy.org/sympy-git.hg git clone --bare git://git.sympy.org/sympy.git hg diff git diff HEAD hg status git status hg status -c git ls-files -t | grep '^H' hg manifest git ls-tree -r --name-only --full-tree HEAD hg parents git show --pretty=format:'%P' -s hg commit git commit -a hg record git add -p; git commit # or, for a more detailed interface: git add -i; git commit hg email -r tip git send-email HEAD^ # or: git format-patch HEAD^ ; git send-email 0001-Add-whitespace.patch hg view gitk, git gui hg help command git help command ~/.hgrc ~/.gitconfig .hg/hgrc .git/config hg paths git remote -v git remote add name url # see "git help remote" for more info how to edit paths; alternatively, you can edit them by hand in editing paths in .hg/hgrc .git/config too .hgignore .gitignore .hg/hgrc [ui] ignore .git/info/exclude hg add git add (note, it adds _content_ to index; can work on a hunk-by-hunk basis with -p!) hg rm git rm hg push git push hg pull git fetch hg pull -u git pull hg addremove git add -A (or: git add .; git ls-files --deleted xargs git rm) hg revert -a git reset --hard hg revert some_file git checkout some_file hg purge git clean -fd hg purge --all git clean -fdx git reset --hard 2fccd4c^ (on a normal repository) hg strip 2fccd4c git reset --soft 2fccd4c^ (on a bare repository) hg export git format-patch hg import --no-commit some.patch git apply some.patch hg import some.patch git am some.patch hg out git fetch && git log origin/master.
    [Show full text]