Mathematics Winter Workshop – 2017
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Maha Eseva Kendra List
महा-ई-सेवा कᴂ 饍ा車ची यादी Sr. VLE Name Palghar CSC Address Location Pincode Mobile Maha E Sewa Kendra Nitin Bhaidas Rampur 1 Rampur Kosbad Road Near 401702 8237635961 Mothe (551636) Market Rampur Jayprakash Gholwad Gholwad Near 2 Ramchandra Gholwad 401702 9860891473 Jalaram Temple Gholwad Bari Bhika Bandu Parnaka Parnaka Parnaka Dahanu (M 3 401602 9637999157 Sonawane Dahanu Cl) Ganpat At-Haladpada Amboli 4 Sukhad Halapada 401606 9960227641 Shishane Road Haladpada Dhangda Nr Saideep Hospital At Post Malyan Tq Dhanu Amul Ramdas Dahanu (M 5 East Dist Thane-401602 401602 9967910609 Tandel Cl) Malyan Sai Deep Hospital Dahanu E Santosh Muskan S S Sanstha 6 Ramchandra 16,Sidhhi Complex,Kasa Kasa Kh. 401607 9049494194 Patil Dahanu Jawhar Road Gayatri Enterprizes, Muskan 16,Siddhicomplex, 7 Swayamrojgar 16,Siddhicomplex Dahanu Kasa Kh. 401607 9049494194 Seva Sahakari Jawhar Road Near Bank Of Maharashtra Kasa Jahir Kasim Maha E Seva Kendra 8 Vangaon 401103 9423533665 Shaikh Chinchani Road Vangaon Maha E Seva Kendra Jayvanti Dahanu (M 9 Dahanu Fort Near Ganesh 401601 9273039057 Rajendra Bari Cl) Mandir Tahsildar Office Maha E Seva Center Dhakti Dahanu Dhakti Dhakti 10 Kishor R Bari 401601 9860002524 Dahanu Bariwada Near Bus Dahanu Stop Maha E Seva Kendra Bordi Akshay 11 Shop No 511 Netaji Road Bordi 401701 8149107404 Bprakash Raut Opp Ram Mandir Bordi Muskan Maha E Seva Kendra 12 Swayamrojgar Ashagad 401602 7066822781 Ashagad Seva Sahakari Maha E-Seva Kendra 2 Prafful Dahanu-Vangaon Road 13 Jaywant Saravali 401602 8087930398 Near Savta Bridge Vaidya Ghungerpada At Dhundalwadi Darshana Dhundalwad 14 Dhundalwadi Talathi 401606 9765284663 Vilas Hilim i Office Ramij Kashim Maha E Seva Kendra 15 Aine 401103 9423533665 Shaikh Charoti Road Aina Maha E Seva Center Chinchani Vangaon Naka 01 Prathomasatv Bulding Chinchani 16 Kishor R Bari 401503 9860002524 Dahanu Khadi - Boisar (Ct) Road Near State Bank A.T.M. -

Nepali Times, but Only About the Kathmandu District Are You Writing an Article
#217 8-14 October 2004 20 pages Rs 25 Weekly Internet Poll # 157 Q. Should the government announce a unilateral ceasefire before Dasain? Peace by peace Total votes:1,001 ANALYSIS by KUNDA DIXIT Hope is strongest Weekly Internet Poll # 158. To vote go to: www.nepalitimes.com Q. Do you think the human rights situation in s Dasain approaches there are indications that both sides will Nepal has improved or deteriorated in the when things seem most hopeless past one year? observe an unofficial festival truce, but prospects of peace A talks to resolve the conflict are more remote than ever. A purported statement from the Maoists declaring a Dasain-Tihar ceasefire on Tuesday turned out to be a hoax. Rebel spokesman Krishna Bahadur Mahara set the record straight by dashing off an e- statement, but that was followed on Wednesday by another release purportedly signed by Prachanda saying the original statement was correct and action would be taken against Mahara. Analysts do not rule out the possibility of army disinformation at work, and see signs of a rift in the Maoist hierarchy following the groups plenum in Dang last month which reportedly rejected peace talks for now. The meeting was followed by strident anti-Indian rhetoric and an intriguing silence on the part of Baburam Bhattarai, who is said to have favoured a softer line on India. The contradictions between central-level statements about links to fraternal parties and recent attacks on the leftist United Peoples Front in the mid-west hint at a breakdown in control. While the leadership calls on UN mediation, grassroots militia defy international condemnation of forced recruitment of school students, abduction of a Unicef staffer and looting of WFP aid. -

High Court of Delhi Advance Cause List
HIGH COURT OF DELHI ADVANCE CAUSE LIST LIST OF BUSINESS FOR FRIDAY,THE 19TH JULY,2013 INDEX PAGES 1. APPELLATE JURISDICTION 1 TO 43 2. SPECIAL BENCH (APPLT. SIDE) 44 TO 54 3. COMPANY JURISDICTION 55 TO 60 4. ORIGINAL JURISDICTION 61 TO 74 5. REGISTRAR GENERAL/ 75 TO 90 REGISTRAR(ORGL.)/ REGISTRAR (ADMN.)/ JOINT REGISTRARS(ORGL). 19.07.2013 1 (APPELLATE JURISDICTION) COURT NO. 1 (DIVISION BENCH-1) HON'BLE THE ACTING CHIEF JUSTICE HON'BLE MR. JUSTICE VIBHU BAKHRU FOR ADMISSION _______________ 1. LPA 822/2012 DELHI DEVELOPMENT AUTHORITY SHOBHANA TAKIAR AND CM APPL. 21045/2012 Vs. DIGVIJAY SINGH ASSOCIATES CM APPL. 21046/2012 2. LPA 4/2013 DELHI TRANSPORT CORPORATION AVNISH AHLAWAT CM APPL. 47/2013 Vs. RANBIR SINGH 3. LPA 477/2013 SRI SATISH KUMAR AGGARWAL Without Generate Vs. GOVT OF ANDHRA PRADESH AND ORS 4. W.P.(C) 4309/2013 MAHANAGAR TELEPHONE NIGAM CHANDAN KUMAR CM APPL. 10006/2013 LTD. CM APPL. 10007/2013 Vs. UNION OF INDIA AND ORS. AFTER NOTICE MISC. MATTERS ____________________________ 5. LPA 666/2006 D.T.C. MR.ARUN KUMAR ARORA,MR.ANIL CM APPL. 5904/2006 Vs. KANWAR SINGH MITTAL,AVNISH AHLAWAT 6. LPA 434/2007 AIRPORTS AUTHORITY OF INDIA MR.DIGVIJAY RAI,SHARMA Vs. JEET SINGH AND ORS. ATUL,SHRUTI VERMA,MR. RAVI VERMA,MR. SANJAY PODDAR,KHAITAN 7. LPA 571/2008 NARENDER KUMAR BANSAL SUDHIR K. LUTHRA,ASHOK Vs. ENGINEERS INDIA LTD. AND SAPRA,GULAL CHAWLA,VK KAUSHAL ORS. 8. LPA 1006/2011 BALWAN SINGH AND ANR ML CHAWLA,AK MISHRA Vs. INDIRA GANDHI NATIONAL CENTRE FOR THE ARTS 9. -

List of Books in Collection
Book Author Category Biju's remarks Mera Naam Joker Abbas K.A Novel made into a film by and starring Raj Kapoor Zed Abbas, Zaheer Cricket autobiography of the former Pakistan cricket captain Things Fall Apart Achebe, Chinua Novel Nigerian writer Aciman, Alexander and Rensin, Twitterature Emmett Novel Famous works of fiction condensed to Twitter format The Hitchhiker's Guide To The Galaxy Adams, Douglas Science Fiction a trilogy in four parts The Dilbert Future Adams, Scott Humour workplace humor by the former Pacific Bell executive The Dilbert Principle Adams, Scott Humour workplace humor by the former Pacific Bell executive The White Tiger Adiga, Aravind Novel won Booker Prize in 2008 Teachings of Sri Ramakrishna Advaita Ashram (pub) Essay great saint and philosopher My Country, My Life Advani L.K. Autobiography former Deputy Prime Minister of India Byline Akbar M.J Essay famous journalist turned politician's collection of articles The Woods Alanahally, Shrikrishna Novel translation of Kannada novel Kaadu. Filmed by Girish Karnad Plain Tales From The Raj Allen, Charles (ed) Stories tales from the days of the British rule in India Without Feathers Allen, Woody Play assorted pieces by the Manhattan filmmaker The House of Spirits Allende, Isabelle Novel Chilean writer Celestial Bodies Alharthi, Jokha Novel Omani novel translated by Marilyn Booth An Autobiography Amritraj, Vijay Sports great Indian tennis player Brahmans and Cricket Anand S. Cricket Brahmin community's connection to cricket in the context of the movie Lagan Gauri Anand, -

National Judicial Academy Verbatim Report
NATIONAL JUDICIAL ACADEMY “SEMINAR ON SENTENCING IN CRIMINAL CASES FOR HIGH COURT JUSTICES HEADING CRIMINAL DIVISION” th th 4 March to 6 March 2016, P-976 VERBATIM REPORT Submitted by MILIND BHASKAR GAWAI Research Fellow NJA, Bhopal, M.P i ii Table of Contents SESSION 1 ................................................................................................................................................ 1 SUBJECT: SENTENCING PHILOSOPHIES ................................................................................................... 1 RESOURCE PERSONS: PROF. K. CHOCKALINGAM ................................................................................... 1 SESSION:2 .............................................................................................................................................. 21 SUBECT: TRADITIONAL AND EMERGINGAPPROACHES TO SENTENCING ............................................. 21 RESOURCE PERSON: DR. USHA RAMNATHAN ...................................................................................... 21 SESSION 3 .............................................................................................................................................. 38 SUBJECT: SENTENCING FOR CASTE BASED ATROCITIES ........................................................................ 38 RESOURCE PERSONS: MR. V. RAMESH NATHAN .................................................................................. 38 SESSION 4 ............................................................................................................................................. -

Sdepromotion08072021.Pdf
File No : BSNLCO-PRII/13/11/2020-PERS-II Dated : 08-07-2021 Annexure S NO Name (Shri/Mrs./Ms.) HRMS No.DOB Rec. Yr. Present Circle DD MM YYYY 1 GEESH KAUSHIK 198810076 8 5 1962 1989 CNTX-N 2 Saikhom Kumar Singh 198313041 1 1 1964 1993 NE-II 3 D S RATHORE 200001705 16 6 1973 1994 MP 4 AVANISH KUMAR CHATURVEDI 199005622 15 8 1962 1996 CNTX-W 5 YOGESH SHARMA 199102111 23 5 1969 1998 CG 6 ANUPAM CHAKRAVARTHY 198917000 1 5 1968 1998 ASM 7 Lalit Mohan Sharma/Lalit Mohan 199501454 29 8 1972 1999 PB 8 NILIM SAIKIA 199103821 30 7 1968 1999 ASM 9 JITENDRA KR. SHUKLA 199102227 25 6 1970 1999 UPE 10 ANIL CHANDRA SARKAR 199002892 19 7 1961 1999 CTD 11 DESH DEEPAK SRIVASTAVA 198605333 1 7 1962 1999 UPE 12 N.VENKATARAMANA 199002531 1 4 1964 1999 AP 13 SURINDER KUMAR SHARMA 198318183 3 10 1961 1999 HR 14 NAND KISHORE SHARMA 198310831 25 12 1961 1999 HR 15 VIRENDER KUMAR SHARMA 199003117 19 4 1969 1999 HR 16 SANJEEV KUMAR MISHRA 199208718 28 7 1972 1999 UP(E) 17 Basant Kumar Singh 199002995 2 12 1967 1999 IN 18 Bhagath Singh B. 199306100 20 7 1969 2000 KTK 19 KRISHNA KANTA MONDAL 199003348 8 6 1966 2001 CTD 20 S.SRINIVAS RAO 200203881 20 8 1974 2001 TLGN 21 NAREN SUTRADHAR 200202903 12 1 1972 2001 CNTX-E 22 KALYAN KUMAR GANDRALA 200201262 5 8 1978 2001 AP 23 MALYADRI ONGOLE 200202509 1 6 1978 2001 AP 24 KARPAGAVALLI B 200200976 1 4 1979 2001 TN 25 SUSHMA PIPLIA 200201263 1 2 1972 2001 RAJ 26 Alok Kumar 200202023 1 7 1977 2001 UPW 27 SRIHARI MEDIDA 200202942 4 6 1976 2001 AP 28 A.NAGARAJAN 200203914 6 12 1976 2001 TN 29 SASIKALA S 200204683 7 6 1977 2001 -

Director/Propriter/Partner Office Mobile No
LICENSE LICENSE VALID S.No. AGENCY NAME Director/Propriter/Partner Office Mobile No. LICENCE AREA L. NO. Off-Distt. ISSUED UP TO DESERT HAWK EX-SERVICEMEN Raghuveer Singh A-6, Vinobha Bhave 2350332, 1 WELFARE CO-OPRETIVE B-78,Vinobha Bhave Nagar,Vaishali Nagar,Vaishali Nagar, All Rajasthan 1/STATE 17.03.2007 16.03.2022 Jaipur 2359257 SOCIETY LTD. Nagar,Jaipur Jaipur MARU PRAHRI SEVA NIVRAT Zor Singh SURKSHA BAL SAINIK Nehru Nagar , Barmer 222052, Barmer, Jaisalmer, 2 INVESTIGATION WELFARE CO- Nehru Nagar , Barmer 10/STATE 19.06.2007 18.6.2022 Barmer 9414755889 Jalore, Jodhpur, Pali PORETIVE SOCIETY LTD. BARMER BHILWARA ZILA EX- Umrao Singh Rathore Ashok Leyland Chraha, 3 SERVICEMEN WELFARE 36-1,Babu Nagar, Bhilwara. 2244202 All Rajasthan 12/STATE 25.06.2007 24.6.2022 Bhilwara Pur Road, Bhilwara SAHKARI SAMITI LTD. CHITTORGARH EX-SERVICEMEN Gheesu Lal Khatik 62, Pratap Nagar, 2244203, 4 WELFARE CO-OPRETIVE 10-E-56,Tilak Nagar,Bhilwara All Rajasthan 13/STATE 25.06.2007 24.6.2022 Chittorgarh Chittorgarh 9829517418 SOCIETY LTD. Satya Narayan Pareek 5 RELIANCE SECURITY SERVICES Pur Road, Bhilwara 9414113217 All Rajasthan 21/STATE 30.07.2007 29.7.2022 Bhilwara 66, Subhash Nagar, Bhilwara Jagdish Prasad Sharma KUMBHJI DARBAR SECURITY E-52 A, Prem Nagar, 2342556, Jaipur, Tonk, Jodhpur, 6 E-73, Prem Nagar, Jhotwara, Jaipur. 22/STATE/ 06.08.2007 05.08.2022 Jaipur SERVICES Jhotwara, Jaipur 9928300117 Alwar, Udaipur Ramesh Pimple 022-26396050, CENTRAL INVESTIGATION & 102-A, Panchmukh Panch, Andheri 46, Vallabh Nagar Ext. 7 9821109295, All Rajasthan 28/STATE 03.09.2007 2.9.2022 Kota SECURITY SERVICE LTD. -

LOK SABHA DEBAT~S (English Version)
Weclaescla" March 19, 1986 Eight" Serle., Vol. XIV No. l' Plaalguaa 28, 1907 (&aka) • LOK SABHA DEBAT~S (English Version) Fifth Session (Eighth Lok Sabha) ( Vol. XIV contains Nos. 11 to 20 ) LOK SABRA SECRETARIA. T NEW DELHI Price: Ra. 4.00 [Orilinal EnSliih proceedinp included ill Enllisla Version and Original Hindi proceedinss -inCluded in Hinc1i VenioD Will be treated as authoritative and not the traoSJatioD tbeRof.) COLUMNS Oral ~nswers to Q~estions : ·Starred Questions Nos. 346 to 3S1 and 3SS 1-35 Written Answers to Questions : 35-169 Starred QueStions Nos. 353, 354, 356 to. 366 3S-47 Un starred Questions Nos. 3375 to 3390, and 3392 to 3501 47-]69 Question of Privilege Against Shri S. B. Chavan, Fonner Minister of Home Affairs and Shri Arun Nehru, Minister of State in the Department of Internal Security. 16~-173 Papers Laid on the Table 174-176 MClsaae from Rajya. Sabba 176 Announcement Re : Group Photograph of ~Iembers 176-177 Committee OD Private Members' Bills and Resolutfons- 177 Fourteenth Report-· Pre::,ented Public Accounts ComRl,i~te.e- , 177 TwentY·Sixth and Twenty Seventh Reports- Presented '·Tho Siln+marked above the n~tllC of a ,Memb~r indioA.te, that the question Wli .....U, 'asked OQ' th~ floo.r or the HO\1se by that Member ~ (il) COLUMN. STATEMENTS UNDER DIRECTION 11~ 178-112 (1) Rc: Infornlation given by Minister of State in the Department or Agri.. culture and Cooperation on 10th March 1986 during the discussion on drouaht and Katural Cal~mitie8. Shri P. Kolandaivelu 878 (il) In reply to the points made by Sbri P. -

Negotiating Modernity in the Novels of Shashi Deshpande
NEGOTIATING MODERNITY IN THE NOVELS OF SHASHI DESHPANDE A Thesis Submitted to the University of North Bengal For the Award of Doctor of Philosophy in English BY AMITABH ROY GUIDE Professor (Dr) Soumyajit Samanta Department of English University of North Bengal June, 2016 Abstract The term ‘tradition’ is a comprehensive one and is inclusive of all social conventions, norms, cultural practices, faiths and beliefs, familial and familiar relationships. The ever imposing burden of traditional authority often succeeds in creating a sense of rebellion against the cumulative forces of oppression and injustice to women. Shashi Deshpande strives to upheld the idea that women must try to overcome their suppressed roles. Her novels depict strong women protagonists who refuse to get crushed and give in to the weight of their personal tragedies, and face life with great courage and strength. The objective of my study is to analyze Shashi Deshpande’s novels placing them in social and realistic perspective. The studies done so far mainly focus on Shashi Deshpande either from a postcolonial point of view or discuss them from a feminist standpoint. But I have tried to look into these novels from a different point altogether. The conflict between conventional social norms and modern thought is placed together to bring out the radical development of the worldview regarding age old customs and social norms. Deshpande seeks to find solutions for problems of women and children within the familial framework and does not preach any abolition of institutions. Yet her approach to social problems and long nurtured rituals force us to consider human relationship and the progressive journey to modernity in a new light. -
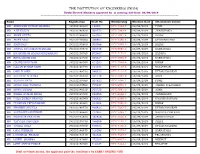
THE INSTITUTION of ENGINEERS (INDIA) Newly Elected Members Approved by at Metting 220 Date: 06/09/2019 ======
THE INSTITUTION OF ENGINEERS (INDIA) Newly Elected Members approved by at metting 220 Date: 06/09/2019 ===================================================================================================== Name Registration Draft No Membership Election Date Attachment Centre MR ABHISHEK KUMAR SHARMA 190202148540 190221 ST717084-5 06/09/2019 PUNE MR AJIT KUJUR 190202148630 000572 ST717093-4 06/09/2019 JHARKHAND MR AMAN GUPTA 190202148610 453285 ST717091-8 06/09/2019 BIHAR MR AMAN NEGI 190202148580 388902 ST717088-8 06/09/2019 UTTARAKHAND MR ANISH RAJ 190202148600 000566 ST717090-5 06/09/2019 BIHAR MR ANISUL ROHOMAN GHARAMI 190202145540 000426 ST716965-0 06/09/2019 KARNATAKA MR BHARATHAM RAGHAVENDRARAVI 190202150760 972467 ST717175-2 06/09/2019 KADAPA MR BHOLANATH DAN 190202145550 000425 ST716966-9 06/09/2019 KARNATAKA MR CHANDAN KUMAR 190202148590 453283 ST717089-6 06/09/2019 BIHAR MR GAGAN KUMAR SAINI 190202148770 103073 ST717107-8 06/09/2019 RAJASTHAN MR ISHU TOMER 190202148720 546522 ST717102-7 06/09/2019 UTTAR PRADESH MR KULDEEP SHARMA 190202148520 501719 ST717082-9 06/09/2019 AGRA MR KUSHAL PATIL 190202148560 004823 ST717086-1 06/09/2019 PUNE MR MOHD ASIF TANTRAY 190202145590 745227 ST716970-7 06/09/2019 JAMMU & KASHMIR MR MONU KUMAR 190202148510 501720 ST717081-0 06/09/2019 AGRA MR NIKHIL KUMAR SINGH 190202145580 896096 ST716969-3 06/09/2019 JHARKHAND MR PAILA DURGA PRASAD 190202140090 766823 ST716769-0 06/09/2019 VISAKHAPATNAM MR PUSHPAM PRIYADARSHI 190202148680 453284 ST717098-5 06/09/2019 BIHAR MR SHOBHIT SHUKLA 190202148570 406433 -

Report on Utilization of Funds Received from IIT Bombay Heritage Fund Inc., USA & Alumni in India for Year 2008-09
Report on Utilization of Funds Received From IIT Bombay Heritage Fund Inc., USA & Alumni in India for Year 2008-09 Office of the Dean, Alumni & Corporate Relations, Indian Institute of Technology Bombay Mumbai, India September 2009 1 2 TABLE OF CONTENTS S.No. TITLE PAGE No. A. Introduction 5 B. Student Development 8 B1. Fellowships 10 B2. Scholarships 20 B3. SDF (Student Development Fund) 28 B4. Loan Scholarships (Class of ‟81) 29 B5. Awards 36 C. Faculty Development 38 C1. Chair Professorships 40 C2. Faculty Development Fund 1 {FDF1} – IITB Heritage Fund 44 C3. Endowment – Faculty Development Fund (Class of ‟87) – {FDF2} 47 C4. Excellence in Teaching Awards 48 C5. Faculty Housing Project (Class of „77) 50 C6. Young Faculty Award (Class of ‟82 & Class of „83) 52 C7. Research Awards 54 D. Infrastructure Development 55 D1. Convention Center 55 D2. Gymkhana 57 D3. Shenoy Design Studio 59 E. Class Projects 60 E1. Endowment - Hostel Maintenance (Class of „72) 62 E2. Endowment - Powai Lake Project (Class of „80) 62 E3. Endowment – “Gurudakshina” Project (Class of ‟83) 63 F. Other Projects/ Endowments 64 F1. Suman Mashruwala Micro Mechanical Systems Lab – Raj Mashruwala 66 F2. Endowment – Wadhwani Electronics Lab 69 F3. Endowment - Library Journals & Sci Finder 72 F4. Endowment - Prof. S.P. Sukhatme Endowment Fund 74 G. Acknowledgement 78 3 4 A. INTRODUCTION It is my pleasure to greet the Alumni and Industry well wishers of the Institute and present this Annual Report on Utilization of Funds for the year 2008-09. A brief summary of the notable events in 2008-09 follows. -

Sl. No. Roll No. Form No. Candidate Name Father Name Marks in Online Test 1 664210 101281 AABID KHAN SHEKH ABDUL ISLAM SHEKH 28
RUHS Paramedical UG/Diploma Entrance Examination 2017 held on 23-July-2017 Provisional Result Sl. Roll Form Candidate Name Father Name Marks in No. No. No. Online test 1 664210 101281 AABID KHAN SHEKH ABDUL ISLAM SHEKH 28 2 664173 104675 AADIL QURESHI AABID HUSSAIN QURESHI 34 3 664254 103571 AADITAYA DUTT BHARDWAJ OM PRAKASH SHARMA 36 4 661541 104433 AADITYA SHARMA PUSHPENDRA SHARMA 33 5 660821 103926 AAKANKSHA TAILOR NAND KISHOR TAILOR 34 6 664171 103910 AAKASH CHAMPA LAL 33 7 663320 100850 AAKASH TAPEN SURESH CHAND TAPEN 28 8 664755 105508 AANAM QURESHI MOHD. ISLAM 35 9 663211 106302 AANCHAL SUMAN SURESH SUMAN 30 10 660755 102990 AARAV YADAV JAI NARAYAN YADAV 27 11 662367 104004 AAROHEE SHARMA KISHAN LAL LOKNATHKA 18 12 662475 101198 AARTI CHOUHAN CHITTAR MAL CHOUHAN 44 13 661835 100122 AARTI GURJAR DEVKARAN GURAJAR 19 14 662629 107199 AARTI KALWAR BABU LAL KALWAR 29 15 662405 100205 AARTI MEENA AMAR SINGH MEENA 28 16 664472 102676 AARTI SHARMA MAHESH SHARMA 44 17 662166 104386 AARTI TIWARI KANHAIYA LAL TIWARI 24 18 663818 106318 AARTI YADAV RAM SINGH YADAV 22 19 662886 101899 AASHISH DADHICH RAJENDRA PRASAD SHARMA 41 20 661324 102868 AASHISH KUMAR MITTAL GOPAL PRASAD MITTAL 41 21 663185 105401 AASHIYA ANSAR M.D. ANSAR 38 22 661824 105874 AASTHA UPADHYAY RAJENDRA UPADHYAY 86 23 663952 102920 AAYSHA BANO MOHAMMED YUSUF 35 24 662342 106797 AAYUSH JAGDISH PRASAD 40 25 662713 102355 AAYUSH KUMAR TANWAR GHANSHYAM TANWAR 24 26 664548 101902 AAYUSH PARASHAR LALIT MOHAN PARASHAR 35 27 663595 101434 AAYUSHI GEHLOT RAMESH GEHLOT 46 28 662619