Modeling of Direct Torque Control (DTC) of BLDC Motor Drive
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

High Speed Linear Induction Motor Efficiency Optimization
Calhoun: The NPS Institutional Archive Theses and Dissertations Thesis Collection 2005-06 High speed linear induction motor efficiency optimization Johnson, Andrew P. (Andrew Peter) http://hdl.handle.net/10945/11052 High Speed Linear Induction Motor Efficiency Optimization by Andrew P. Johnson B.S. Electrical Engineering SUNY Buffalo, 1994 Submitted to the Department of Ocean Engineering and the Department of Electrical Engineering and Computer Science in Partial Fulfillment of the Requirements for the Degree of Naval Engineer and Master of Science in Electrical Engineering and Computer Science at the Massachusetts Institute of Technology June 2005 ©Andrew P. Johnson, all rights reserved. MIT hereby grants the U.S. Government permission to reproduce and to distribute publicly paper and electronic copies of this thesis document in whole or in part. Signature of A uthor ................ ............................... D.epartment of Ocean Engineering May 7, 2005 Certified by. ..... ........James .... ... ....... ... L. Kirtley, Jr. Professor of Electrical Engineering // Thesis Supervisor Certified by......................•........... ...... ........................S•:• Timothy J. McCoy ssoci t Professor of Naval Construction and Engineering Thesis Reader Accepted by ................................................. Michael S. Triantafyllou /,--...- Chai -ommittee on Graduate Students - Depa fnO' cean Engineering Accepted by . .......... .... .....-............ .............. Arthur C. Smith Chairman, Committee on Graduate Students DISTRIBUTION -

United States Patent (19) 11 4,343,223 Hawke Et Al
United States Patent (19) 11 4,343,223 Hawke et al. 45) Aug. 10, 1982 54 MULTIPLESTAGE RAILGUN UCRL-52778, (7/6/79). Hawke. 75 Inventors: Ronald S. Hawke, Livermore; UCRL-82296, (10/2/79) Hawke et al. Jonathan K. Scudder, Pleasanton; Accel. Macropart, & Hypervel. EM Accelerator, Bar Kristian Aaland, Livermore, all of ber (3/72) Australian National Univ., Canberra ACT Calif. pp. 71,90–93. LA-8000-G (8/79) pp. 128, 135-137, 140, 144, 145 73) Assignee: The United States of America as (Marshall pp. 156-161 (Muller et al). represented by the United States Department of Energy, Washington, Primary Examiner-Sal Cangialosi D.C. Attorney, Agent, or Firm-L. E. Carnahan; Roger S. Gaither; Richard G. Besha . - (21) Appl. No.: 153,365 57 ABSTRACT 22 Filed: May 23, 1980 A multiple stage magnetic railgun accelerator (10) for 51) Int. Cl........................... F41F1/00; F41F 1/02; accelerating a projectile (15) by movement of a plasma F41F 7/00 arc (13) along the rails (11,12). The railgun (10) is di 52 U.S. Cl. ....................................... ... 89/8; 376/100; vided into a plurality of successive rail stages (10a-n) - 124/3 which are sequentially energized by separate energy 58) Field of Search .................... 89/8; 124/3; 310/12; sources (14a-n) as the projectile (15) moves through the 73/12; 376/100 bore (17) of the railgun (10). Propagation of energy from an energized rail stage back towards the breech 56) References Cited end (29) of the railgun (10) can be prevented by connec U.S. PATENT DOCUMENTS tion of the energy sources (14a-n) to the rails (11,12) 2,783,684 3/1957 Yoler ...r. -

Permanent Magnet DC Motors Catalog
Catalog DC05EN Permanent Magnet DC Motors Drives DirectPower Series DA-Series DirectPower Plus Series SC-Series PRO Series www.electrocraft.com www.electrocraft.com For over 60 years, ElectroCraft has been helping engineers translate innovative ideas into reality – one reliable motor at a time. As a global specialist in custom motor and motion technology, we provide the engineering capabilities and worldwide resources you need to succeed. This guide has been developed as a quick reference tool for ElectroCraft products. It is not intended to replace technical documentation or proper use of standards and codes in installation of product. Because of the variety of uses for the products described in this publication, those responsible for the application and use of this product must satisfy themselves that all necessary steps have been taken to ensure that each application and use meets all performance and safety requirements, including all applicable laws, regulations, codes and standards. Reproduction of the contents of this copyrighted publication, in whole or in part without written permission of ElectroCraft is prohibited. Designed by stilbruch · www.stilbruch.me ElectroCraft DirectPower™, DirectPower™ Plus, DA-Series, SC-Series & PRO Series Drives 2 Table of Contents Typical Applications . 3 Which PMDC Motor . 5 PMDC Drive Product Matrix . .6 DirectPower Series . 7 DP20 . 7 DP25 . 9 DP DP30 . 11 DirectPower Plus Series . 13 DPP240 . 13 DPP640 . 15 DPP DPP680 . 17 DPP700 . 19 DPP720 . 21 DA-Series. 23 DA43 . 23 DA DA47 . 25 SC-Series . .27 SCA-L . .27 SCA-S . .29 SC SCA-SS . 31 PRO Series . 33 PRO-A04V36 . 35 PRO-A08V48 . 37 PRO PRO-A10V80 . -

Magnetism Known to the Early Chinese in 12Th Century, and In
Magnetism Known to the early Chinese in 12th century, and in some detail by ancient Greeks who observed that certain stones “lodestones” attracted pieces of iron. Lodestones were found in the coastal area of “Magnesia” in Thessaly at the beginning of the modern era. The name of magnetism derives from magnesia. William Gilbert, physician to Elizabeth 1, made magnets by rubbing Fe against lodestones and was first to recognize the Earth was a large magnet and that lodestones always pointed north-south. Hence the use of magnetic compasses. Book “De Magnete” 1600. The English word "electricity" was first used in 1646 by Sir Thomas Browne, derived from Gilbert's 1600 New Latin electricus, meaning "like amber". Gilbert demonstrates a “lodestone” compass to ER 1. Painting by Auckland Hunt. John Mitchell (1750) found that like electric forces magnetic forces decrease with separation (conformed by Coulomb). Link between electricity and magnetism discovered by Hans Christian Oersted (1820) who noted a wire carrying an electric current affected a magnetic compass. Conformed by Andre Marie Ampere who shoes electric currents were source of magnetic phenomena. Force fields emanating from a bar magnet, showing Nth and Sth poles (credit: Justscience 2017) Showing magnetic force fields with Fe filings (Wikipedia.org.) Earth’s magnetic field (protects from damaging charged particles emanating from sun. (Credit: livescience.com) Magnetic field around wire carrying a current (stackexchnage.com) Right hand rule gives the right sign of the force (stackexchnage.com) Magnetic field generated by a solenoid (miniphyiscs.com) Van Allen radiation belts. Energetic charged particles travel along B lines Electric currents (moving charges) generate magnetic fields but can magnetic fields generate electric currents. -

Discrete and Continuous Model of Three-Phase Linear Induction Motors “Lims” Considering Attraction Force
energies Article Discrete and Continuous Model of Three-Phase Linear Induction Motors “LIMs” Considering Attraction Force Nicolás Toro-García 1 , Yeison A. Garcés-Gómez 2 and Fredy E. Hoyos 3,* 1 Department of Electrical and Electronics Engineering & Computer Sciences, Universidad Nacional de Colombia—Sede Manizales, Cra 27 No. 64 – 60, Manizales, Colombia; [email protected] 2 Unidad Académica de Formación en Ciencias Naturales y Matemáticas, Universidad Católica de Manizales, Cra 23 No. 60 – 63, Manizales, Colombia; [email protected] 3 Facultad de Ciencias—Escuela de Física, Universidad Nacional de Colombia—Sede Medellín, Carrera 65 No. 59A-110, 050034, Medellín, Colombia * Correspondence: [email protected]; Tel.: +57-4-4309000 Received: 18 December 2018; Accepted: 14 February 2019; Published: 18 February 2019 Abstract: A fifth-order dynamic continuous model of a linear induction motor (LIM), without considering “end effects” and considering attraction force, was developed. The attraction force is necessary in considering the dynamic analysis of the mechanically loaded linear induction motor. To obtain the circuit parameters of the LIM, a physical system was implemented in the laboratory with a Rapid Prototype System. The model was created by modifying the traditional three-phase model of a Y-connected rotary induction motor in a d–q stationary reference frame. The discrete-time LIM model was obtained through the continuous time model solution for its application in simulations or computational solutions in order to analyze nonlinear behaviors and for use in discrete time control systems. To obtain the solution, the continuous time model was divided into a current-fed linear induction motor third-order model, where the current inputs were considered as pseudo-inputs, and a second-order subsystem that only models the currents of the primary with voltages as inputs. -

DC Motor Workshop
DC Motor Annotated Handout American Physical Society A. What You Already Know Make a labeled drawing to show what you think is inside the motor. Write down how you think the motor works. Please do this independently. This important step forces students to create a preliminary mental model for the motor, which will be their starting point. Since they are writing it down, they can compare it with their answer to the same question at the end of the activity. B. Observing and Disassembling the Motor 1. Use the small screwdriver to take the motor apart by bending back the two metal tabs that hold the white plastic end-piece in place. Pull off this plastic end-piece, and then slide out the part that spins, which is called the armature. 2. Describe what you see. 3. How do you think the motor works? Discuss this question with the others in your group. C. Mounting the Armature 1. Use the diagram below to locate the commutator—the split ring around the motor shaft. This is the armature. Shaft Commutator Coil of wire (electromagnetic) 2. Look at the drawing on the next page and find the brushes—two short ends of bare wire that make a "V". The brushes will make electrical contact with the commutator, and gravity will hold them together. In addition the brushes will support one end of the armature and cradle it to prevent side- to-side movement. 1 3. Using the cup, the two rubber bands, the piece of bare wire, and the three pieces of insulated wire, mount the armature as in the diagram below. -

Electric Vehicle Modeling Utilizing DC Motor Equations
1 Electric Vehicle Modeling Utilizing DC Motor Equations Clay S. Hearn, Damon A. Weeks, Richard C. Thompson, and Dongmei Chen Abstract— This paper discusses modeling an electric utility vehicle powered by a separately wound DC motor. Many modeling techniques use steady state efficiency maps and torque- speed curves to describe the performance of electric motors, which can overlook transient response dynamics, current limits, and thermal limits that may affect the end vehicle performance. This paper discusses using bond-graph techniques to develop a causal model of an electric vehicle powered by a separately wound DC motor and development of the appropriate feed- forward and feed-back controllers required for route following. The causal model performance is compared to a PSAT model of the same electric vehicle, which uses motor torque-speed curve and efficiency map. Fig. 1. Columbia ParCar SUV-LN electric utility vehicle Index Terms—dc motors, PSAT, bond graphs, modeling, and for particular applications. The Center for Electromechanics electric vehicle has successfully used PSAT in the past to predict on-route energy usage of a plug-in hydrogen fuel cell shuttle bus. I. INTRODUCTION Tuned PSAT model predictions of energy consumption matched data collected from on-road testing to within 5% [1]. ll electric utility vehicles such as the Columbia ParCar PSAT is considered a forward looking model since a A SUV-LN, shown in Figure 1, are used in a wide variety controlled drive torque demand is used to control the vehicle of industrial and commercial applications where tools, following a particulate route. From the motor torque and equipment, and personnel need to be transported efficiently vehicle speed, quasistatic model techniques are used to track with zero emissions. -
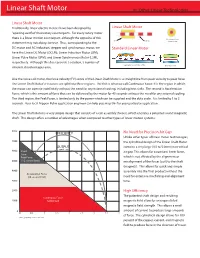
Linear Shaft Motor Vs
Linear Shaft Motor vs. Other Linear Technologies Linear Shaft Motor Traditionally, linear electric motors have been designed by Linear Shaft Motor “opening out flat” their rotary counterparts. For every rotary motor there is a linear motion counterpart, although the opposite of this No influence from Coil Magnets statement may not always be true. Thus, corresponding to the change in gap DC motor and AC induction, stepper and synchronous motor, we Standard Linear Motor have the Linear DC Motor (DCLM), Linear Induction Motor (LIM), Linear Pulse Motor (LPM), and Linear Synchronous Motor (LSM), respectively. Although this does provide a solution, a number of Cogging by concentration of flux inherent disadvantages arise. Absorption force Like the voice coil motor, the force velocity (FV) curve of the Linear Shaft Motor is a straight line from peak velocity to peak force. The Linear Shaft Motor’s FV curves are split into three regions. The first is what we call Continuous Force. It is the region in which the motor can operate indefinitely without the need for any external cooling, including heat sinks. The second is Acceleration Force, which is the amount of force that can be delivered by the motor for 40 seconds without the need for any external cooling. The third region, the Peak Force, is limited only by the power which can be supplied and the duty cycle. It is limited to 1 to 2 seconds. Your local Nippon Pulse application engineer can help you map this for your particular application. The Linear Shaft Motor is a very simple design that consists of a coil assembly (forcer), which encircles a patented round magnetic shaft. -

Gsm Based Controlling of Coil Gun Using Dtmf Technology
www.ijcrt.org © 2017 IJCRT | Volume 5, Issue 3 September 2017 | ISSN: 2320-2882 GSM BASED CONTROLLING OF COIL GUN USING DTMF TECHNOLOGY 1Jobin Joseph, 2Ramkumar Raju, 3Ghilby Jaison Varghese 1UG Student, 2UG Student, 3Assistant Professor Dept. of CSE, 1Computer Science And Engineering, 1Mar Baselios Christian College of Engineering and Technology, Peermade, India ________________________________________________________________________________________________________ Abstract : Our project GSM based controlling of gun using DTMF technology, is an electromagnetic gun that can be controlled by a person at anywhere around the globe. The system use a DTMF (Dual Tone Multi Frequency) technology for controlling the coil gun. That can be make possible through the support of GSM (Global System for Mobile) network. The controlling process is carried out by the programmed microcontroller (AT89C52), which is more faster. The Electromagnetic Induction can be used to rifle the bullets, So we can easily increase the power of the gun by adding the number of coil stages and increase the number of turns. Our project is one of the safest and secured weapon. Index Terms: GSM, DTMF, ________________________________________________________________________________________________________ I. INTRODUCTION The concept of Triggering/Position/Motion control has evolved since end of 18th century. Simply, triggering/position/motion control means to control the movement of the object accurately based on different physical parameters such as speed, load, distance, inertia etc. individually or a combination of these factors. Different types of techniques are used to control the Coil gun and speed of the AC motor, DC motor or Stepper motor. These methods includes digital or analog inputs, concept of Phase locked loop (PLL) etc. The common means of controlling devices are using switches. -

A Hydraulic Motor-Alternator System for Ocean-Submersible Vehicles
A Hydraulic Motor-Alternator System for Ocean-Submersible Vehicles Harry O. Aintablian, Thomas I. Valdez, Jack A. Jones Jet Propulsion Laboratory, California Institute of Technology. Abstract An ocean-submersible vehicle has been developed at JPL that moves back and forth between sea level and a depth of a few hundred meters. A liquid volumetric change at a pressure of 70 bars is created by means of thermal phase change. During vehicle ascent, the phase-change material (PCM) is melted by the circulation of warm water and thus pressure is increased. During vehicle descent, the PCM is cooled resulting in reduced pressure. This pressure change is used to generate electric power by means of a hydraulic pump that drives a permanent magnet (PM) alternator. The output energy of the alternator is stored in a rechargeable battery that powers an on-board computer, instrumentation and other peripherals. The focus of this paper is the performance evaluation of a specific hydraulic motor-alternator system. Experimental and theoretical efficiency data of the hydraulic motor and the alternator are presented. The results are used to evaluate the optimization of the hydraulic motor-alternator system. The integrated submersible vehicle was successfully operated in the Pacific Ocean near Hawaii. A brief overview of the actual test results is presented. 1 Introduction NASA JPL and Scripps Institute of Oceanography have developed and demonstrated an underwater vehicle that is capable of being powered by natural thermal energy of the ocean. The underwater vehicle (Figure 1) takes advantage of the temperature differences at different ocean depths. Key to its operation is a phase change material (PCM) that melts and expands as the vehicle ascends to warm water causing the pressurization of oil inside the vessel. -

ON Semiconductor Is
ON Semiconductor Is Now To learn more about onsemi™, please visit our website at www.onsemi.com onsemi and and other names, marks, and brands are registered and/or common law trademarks of Semiconductor Components Industries, LLC dba “onsemi” or its affiliates and/or subsidiaries in the United States and/or other countries. onsemi owns the rights to a number of patents, trademarks, copyrights, trade secrets, and other intellectual property. A listing of onsemi product/patent coverage may be accessed at www.onsemi.com/site/pdf/Patent-Marking.pdf. onsemi reserves the right to make changes at any time to any products or information herein, without notice. The information herein is provided “as-is” and onsemi makes no warranty, representation or guarantee regarding the accuracy of the information, product features, availability, functionality, or suitability of its products for any particular purpose, nor does onsemi assume any liability arising out of the application or use of any product or circuit, and specifically disclaims any and all liability, including without limitation special, consequential or incidental damages. Buyer is responsible for its products and applications using onsemi products, including compliance with all laws, regulations and safety requirements or standards, regardless of any support or applications information provided by onsemi. “Typical” parameters which may be provided in onsemi data sheets and/ or specifications can and do vary in different applications and actual performance may vary over time. All operating parameters, including “Typicals” must be validated for each customer application by customer’s technical experts. onsemi does not convey any license under any of its intellectual property rights nor the rights of others. -

Synchronous Motor
CHAPTER38 Learning Objectives ➣ Synchronous Motor-General ➣ Principle of Operation ➣ Method of Starting SYNCHRONOUS ➣ Motor on Load with Constant Excitation ➣ Power Flow within a Synchronous Motor MOTOR ➣ Equivalent Circuit of a Synchronous Motor ➣ Power Developed by a Synchronous Motor ➣ Synchronous Motor with Different Excitations ➣ Effect of increased Load with Constant Excitation ➣ Effect of Changing Excitation of Constant Load ➣ Different Torques of a Synchronous Motor ➣ Power Developed by a Synchronous Motor ➣ Alternative Expression for Power Developed ➣ Various Conditions of Maxima ➣ Salient Pole Synchronous Motor ➣ Power Developed by a Salient Pole Synchronous Motor ➣ Effects of Excitation on Armature Current and Power Factor ➣ Constant-Power Lines ➣ Construction of V-curves ➣ Hunting or Surging or Phase Swinging ➣ Methods of Starting ➣ Procedure for Starting a Synchronous Motor Rotary synchronous motor for lift ➣ Comparison between Ç Synchronous and Induction applications Motors ➣ Synchronous Motor Applications 1490 Electrical Technology 38.1. Synchronous Motor—General A synchronous motor (Fig. 38.1) is electrically identical with an alternator or a.c. generator. In fact, a given synchronous machine may be used, at least theoretically, as an alternator, when driven mechanically or as a motor, when driven electrically, just as in the case of d.c. machines. Most synchronous motors are rated between 150 kW and 15 MW and run at speeds ranging from 150 to 1800 r.p.m. Some characteristic features of a synchronous motor are worth noting : 1. It runs either at synchronous speed or not at all i.e. while running it main- tains a constant speed. The only way to change its speed is to vary the supply frequency (because Ns = 120 f / P).