DOCSLIB.ORG

Speed on Canals.” by FEANCISROUBILIAC CONDER, M

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Speed on Canals.” by FEANCISROUBILIAC CONDER, M 160 ADXISSIONS AND ELECTIONS. [Minutes of Associafe IlIe1r~71err. HORACEALLEN, Stud. Inst.C.E. GEOXGEDALLAS MARSTOX, Stud. Inst. JAMES ATEINSON. C.E. ARTHUR BARCLAY. CHARLESEDWARD MASTERMAN. CHARLESWILLIADX BARNETT. JOHXNETHVEN. FELICIANOMENDES DE MESQUITA \vILLIAM BURTON8bVILLE IIILLS, BARROS. Stud. Inst. C.E. WILLIAM BASHALL, Jun., Stud.Inst. WILLIAU PCRCELLOWEILL, Stud. C.E. Inst. C.E. PERCYBENHAB~, Stud. Inst.C.E. CAHILOGUILLERXO PARDO,Stud. EDWARDROBERT BIRCH, B.A., B.E., Inst. C.E. Stud. Inst. C.E. CHARLES DONALD NAPIERPAREEL HARRYBIRD. HENRYPARKES, Stud. Inst. C.E. WILLIAMNISBET BLAIR, Stud. Inst. WILLIAM MORROPEARSE. C.E. CHARLESBERKELEY PENLINGTOB, CARL RODERIQUELOUIS MENNI BONN. Stud. Inst. C.E. THOXASSMITH BRIGHT,Stud. Inst. WILLIADIFRANK PETTIGREW, Stud. C.E. Inst. C.E. CHARLESEDWIX BROWN. WILLIAXHEXRY RADFORD. WILLIAMHENRY BURR. WILLIAXREID. JAMESBUTLER. PETERROBERTS. ALBERTHAVELOCK CASE. HENRY GEORGEARCHIBALD ROUSE. ALFRED CREER. HEXRYROYLE. FITZHERBERT RUXTOXDESPARD. ROBERT ALLENWILLIAM SNINNERTON. HEXRYFRANCIS DOREY, Stud. Inst. ALBERTHARRISON TURNER. C.E. PERCYJOHN WATES. QEORGEHOLLAND ERSKINE, Stud. Inst. THOMASDUNClN WEIR, Stud.Inst. C.E. C.E. HARRYF~ANCIS. I~AU~IICEFITZGER.4LD WILSON, Stud. JAMESFRENCH. Inst. C.E. ROBERTMACNISH GALE. JOHN i%CKWORTH WOOD. RICHARDHACK. FREDERICKADLARD WRIGHT, Stud. GEORGE HOWARDHARBISON. Inst. C.E. LLOYDHASSELL, Stud. Inst. C.E. ROBERTW.4DE WRIGHT, Stud. Inst. PERDINANDHUDLESTON. C.E. WILLIAMOWEN LGCAS. Associate. WILLIAVWAKEFORD. ‘‘ Speed on Canals.” BY FEANCISROUBILIAC CONDER, M. INST.C.E. THEamount of resistance tothe propulsion of vessels through narrowchannels, due to the size, the form, andthe surface of the channel,has not hitherto been fully studied. Thatthis Downloaded by [ University of Liverpool] on [15/09/16]. Copyright © ICE Publishing, all rights reserved. PLATE 1 e% 120'.0" X 20'.0' FORT H AND C LVD E. 1768. GLOSTER AND BERKLEY. 1793. CALEDONIAN. 1803. WILTS AND BERKS. GLASGOW, AND PAISLEY. 1796. AMSTERDAM. 31865. 1803. 45'"'' X 5'.0" 50'.0"x R'.O' GRANDJUNCTION. MONKLAND 17 DD. NORTH HOLLAND. 1770. 1825. K.CONDER, DEL? DownloadedF by [ University of Liverpool] on [15/09/16]. Copyright © ICE Publishing, all rights reserved. Proceedings.] CONDER ON SPEED ON CANALS. 161 resistanceincreases in some ratio tothe diminution of free mater-way is known. In the ‘Minutes of Proceedings’will be found the statement that asteamer which attained a speed of from 16 to 18 miles an hour at sea, could not make more than from 8 to 9 miles per hour in the narrowest part of the Clyde ; 1 and that a boat which had a speed of 10 miles per hour in the Liffey, could not make more than 7 miles per hour in the Royal Irish Canal.2 The instant acceleration of a boat on passing into deeper water, which was mentioned in the debate cited, is well known to all boating men. But no formula for determining the proportion is to be found in engineering text books. It was the advice of the Author, on being consulted on one of the most important hydraulic projectsof the day, that there should be instituted, in the firstplace, so thorough an investigation of the mainscientific questions involved as to leave no point open to hostiIecriticism. Among the specialsteps recommended to this end was “ the commencement of a series of experiments for deter- mining the form of cross:section best suited for canal navigation.” The recommendation nothaving beencarried out, the Author has endeavoured to apply to theelucidation of the question certain known facts as to the movement of water in channels of various forms, and as to the movement of vessels in open waters. As to the first, the experiments of Darcy and Bazin have been chiefly of use; and as to the second, those of the late Mr. W. Froude, N. Inst. C.E., on the wave-making resistance of ships. Since the commencement of the inquiry, its importance hasbeen accentuated by the extraordinarydegree of attention that has been excited bythe Suez Canal, and by the remarkablephenomenon of the retardation effected in thepassage of vessels, although not amount- ing to an average of five each way per day. The average time occupied in actual movement through the canal hasincreased from seventeen hours pership in1876, to eighteen hours sixteen minutes in 1881, and to eighteen hours fifty-seven minutes in 1882; the speed slackening from 5 * 88 to 5 -47and 5 27 miles per hour. The time passed in the canal by each ressel has risen from thirty-nine hours in 1876, to fifty-three hours forty-six minutes in 1882. And a very recent Report cites three cases of English mail steamers detained for seventy-one hours each in the canal. It is thus un- deniable that the question of canal capacity for transport assumes * Minutes of Proceedings Inst. C.E., vol. xxvi., p. 20. * Ibid., vol. xxvi., p. 32. TILe Times, 20th September, 1883. [THE INST. C.E. VOL. LXXVI.] M Downloaded by [ University of Liverpool] on [15/09/16]. Copyright © ICE Publishing, all rights reserved. 162 CONDER ON SPEED ON CANALS. [Minutes of a foremost rank among the practical engineering problems of the day. In theabsence of direct experiment, the only method available for the purpose of research is the comparative method. By this, mathematical considerations may beillustrated toa certain extent; and it may be at all events hoped to get so far as to determine where direct experiment becomes indispensable. A vessel in its progress is continually displacing a mass of water equal to its own submerged bulk. This mass is usually calcu1at.ed as proportional to the greatest immergedcross-section of the vessel ; an approximationsufficiently close for the presentinquiry. In open water, the vacuum that would otherwise be left in the wake of the vessel is filled by the water rushing infrom all sides. It is unnecessarynow toinquire how this movement of thewater affects the speed of the vessel, as the ordinary performance of the latter inopen water is taken as the unit of comparison. Whenthe movement of a vessel takesplace in a restricted channel, the case is altered. There is no longer an indefinite supply of water all round thevessel to rush into the hollow at the wake. That hollow is filled, eitherby water which follows the movement of the vessel through the canal, or by that which Aows as a counter current, being driven by the head due to the wave caused by the vessel. The first of these two actions is so limited that it may be neglected except in river navigation. The back- ward current, taken alone. will be directly as the speed and as the cross-section of the vessel, and inversely as the free water-way, or excess of t,he cross-section of the canal over that of the vessel. Thus a vessel moving through a restricted channel has to on- counter an opposing current which is a function of her own move- ment. Her speed will be the resultant of her proper motion and of that of the current, inso far asit affects her, and willbe, roughly speaking, the difference of the two speeds. It is thus possible to obtain, subject to further elucidation, a general formula for the retardation of a vessel in a canal due to the back-current produced by her own movement. Let A = the cross-section of the canal ; a= 7) 7, ,) ,) vessel; A n = -. a’ V = the speed in open water ; y = the back-current in thecanal ; X = the speed of the vessel in thecanal. Downloaded by [ University of Liverpool] on [15/09/16]. Copyright © ICE Publishing, all rights reserved. Proceedings.] CONDERON SPEED CANALS.ON 163 Then v=x+y, X and, as the free water-way is equaln - to 1, y = -- n - 1’ therefore v=x+- X 12- 1 (1) Let, for example, 12 = 4. Then v=x+3,X and x=2v. It results, however, from the experilncnts of Darcy and Bazin, as well as from theory, that not only must the area of the channel be regarded, but also its form, and the special nature of the wetted surface. Of all forms of channel, according to this authority, the semi-circular is that which offers least resistance to the flowof water ; as it is also that of which the hydraulic radius is the largest, in proportion to the area. Butthe hydraulic radius, or the areadivided by thewet n perimeter, = is approximately the same for a semi-circle and G,- 2 for a semi-ellipse of equal area. It will be at once admitted that, if an ellipse be taken of which the axes are, forexample, as 6 to 1, it would be rash to assume that the flow of water would be the samethrough two equal semi-elliptical sections, on0 withthe minor axis vertical, and the other with it horizontal. The peri- phery ineach case would be exactlythe same, and thus theordinary formula, as dependent on the hydraulic radius, would be the same, and the volume and weight of water would be the same. But the hydrostatic pressure on the periphery, and therefore the frictional resistance, would be very different. Here, then, is a case where present forlnulas are inadequate fully to investigate the question of speed. For convenience of navigation, the top width of a canal may be generally taken as from 7 to 10 times its depth; and, with the reserve just mentioned, the formula of the hydraulic radius maybe applied to a semi-elliptical section of this proportion as if it were a semi-circle. With this allowance, the formulaabove given, correctedfor any difference of thehydraulic radius, as below exemplified, may be applied to those few facts which are attain- able in the absence of further experiment. The Suez Canal (Fig. 1) has a depth of 26 feet; a bottom width of 72 feet; sides sloping at 2 or 2& to l to within 5 feet of the water-line, and a top width of 326 feet.
Load more

Recommended publications
  • A Beginner's Guide to Boating on Inland Waterways
    Ti r A Beginner’s Guide To Boating On Inland Waterways Take to the water with British Waterways and the National Rivers Authority With well over 4,000 km (2,500 miles) of rivers and canals to explore, from the south west of England up to Scotland, our inland waterways offer plenty of variety for both the casual boater and the dedicated enthusiast. If you have ever experienced the pleasures of 'messing about on boats', you will know what a wealth of scenery and heritage inland waterways open up to us, and the unique perspective they provide. Boating is fun and easy. This pack is designed to help you get afloat if you are thinking about buying a boat. Amongst other useful information, it includes details of: Navigation Authorities British Waterways (BW) and the National Rivers Authority (NRA), which is to become part of the new Environment Agency for England and Wales on 1 April 1996, manage most of our navigable rivers and canals. We are responsible for maintaining the waterways and locks, providing services for boaters and we licence and manage boats. There are more than 20 smaller navigation authorities across the country. We have included information on some of these smaller organisations. Licences and Moorings We tell you everything you need to know from, how to apply for a licence to how to find a permanent mooring or simply a place for «* ^ V.’j provide some useful hints on buying a boat, includi r, ...V; 'r 1 builders, loans, insurance and the Boat Safety Sch:: EKVIRONMENT AGENCY Useful addresses A detailed list of useful organisations and contacts :: : n a t io n a l libra ry'& ■ suggested some books we think will help you get t information service Happy boating! s o u t h e r n r e g i o n Guildbourne House, Chatsworth Road, W orthing, West Sussex BN 11 1LD ENVIRONMENT AGENCY 1 Owning a Boat Buying a Boat With such a vast.range of boats available to suit every price range, .
    [Show full text]
  • INLAND NAVIGATION AUTHORITIES the Following Authorities Are Responsible for Major Inland Waterways Not Under British Waterways Jurisdiction
    INLAND NAVIGATION AUTHORITIES The following authorities are responsible for major inland waterways not under British Waterways jurisdiction: RIVER ANCHOLME BRIDGEWATER CANAL CHELMER & BLACKWATER NAVIGATION The Environment Agency Manchester Ship Canal Co. Essex Waterways Ltd Anglian Region, Kingfisher House Peel Dome, Trafford Centre, Island House Goldhay Way, Orton Manchester M17 8PL Moor Road Peterborough PE2 5ZR T 0161 629 8266 Chesham T 08708 506 506 www.shipcanal.co.uk HP5 1WA www.environment-agency.gov.uk T: 01494 783453 BROADS (NORFOLK & SUFFOLK) www.waterways.org.uk/EssexWaterwaysLtd RIVER ARUN Broads Authority (Littlehampton to Arundel) 18 Colgate, Norwich RIVER COLNE Littlehampton Harbour Board Norfolk NR3 1BQ Colchester Borough Council Pier Road, Littlehampton, BN17 5LR T: 01603 610734 Museum Resource Centre T 01903 721215 www.broads-authority.gov.uk 14 Ryegate Road www.littlehampton.org.uk Colchester, CO1 1YG BUDE CANAL T 01206 282471 RIVER AVON (BRISTOL) (Bude to Marhamchurch) www.colchester.gov.uk (Bristol to Hanham Lock) North Cornwall District Council Bristol Port Company North Cornwall District Council, RIVER DEE St Andrew’s House, St Andrew’s Road, Higher Trenant Road, Avonmouth, Bristol BS11 9DQ (Farndon Bridge to Chester Weir) Wadebridge, T 0117 982 0000 Chester County Council PL27 6TW, www.bristolport.co.uk The Forum Tel: 01208 893333 Chester CH1 2HS http://www.ncdc.gov.uk/ RIVER AVON (WARWICKSHIRE) T 01244 324234 (tub boat canals from Marhamchurch) Avon Navigation Trust (Chester Weir to Point of Air) Bude Canal Trust
    [Show full text]
  • The Monthly Newsletter Published by the AUGUST 2020
    AUGUST 2020 The monthly newsletter published by the Near the “Dirty Duck” Pub Photographed by Tony Osbond Please note that all images in this document are the copyright of either the photographer or The Grantham Canal Society. This month’s update from Mike Stone (Chairman) Heigh-ho, Heigh-ho, It's back to work we go All dressed in our own PPE with CRT life vest. The grass grows even higher, the locks are leaking too. Weeds stopped the trip-boat moving; we didn’t know what to do Heigh-ho, Heigh-ho, Heigh-ho, Heigh-ho We dig up stuff on Fridays we lift out branches too, We’re getting a new weed boat soon but drivers needed too As volunteers on this canal there’s so much work to do Heigh-ho, Heigh-ho, It's back to work we go .... Heigh-ho, Heigh-ho, Heigh-ho, Heigh-ho! Don’t just sing alone – come and join us - Heigh-ho! Heigh-ho! (No height restriction!) Thanks to you, our supporters, we have achieved our target to raise £20,000 to enable the restoration of the slipway at the Depot. This is a brilliant result in four months and the Society says a big THANK YOU to all who contributed. Restoration work will commence early in October – Heigh-ho! Within the coming week we look forward to the delivery of a new, to us, weed-boat from The Rothen Group. Which, by the way, hasn't been named yet - see p10. This will enable us to remove the extensive weed growth from the navigation and, I hope, permit The Three Shires charter cruises to re-commence operation.
    [Show full text]
  • Iwa Submission on the Environment Bill – Appendix A
    IWA SUBMISSION ON THE ENVIRONMENT BILL – APPENDIX A IWA VISION FOR SUSTAINABLE PROPULSION ON THE INLAND WATERWAYS EXECUTIVE OVERVIEW 1. Recognising the UK Government’s strategy to reduce emissions from diesel and petrol engines, IWA formed its Sustainable Propulsion Group in 2019 to identify and monitor developments which will enable boats on the inland waterways to fully contribute to the Government’s stated aim of zero CO2 emissions by 2050. 2. The Group has identified a number potential solutions that it recommends should be progressed in order to ensure that boats used on the inland waterways do not get left behind in technological developments. These are outlined in more detail in this paper. 3. To ensure that the inland waterways continue to be sustainable for future generations, and continue to deliver benefits to society and the economy, IWA has concluded that national, devolved and local government should progress the following initiatives: Investment in infrastructure through the installation of 300 shore power mains connection charging sites across the connected inland waterways network. This would improve air quality by reducing the emissions from stoves for heating and engines run for charging batteries, as well as enabling a move towards more boats with electric propulsion. Working with navigation authorities, investment in a national dredging programme across the inland waterways to make propulsion more efficient. This will also have additional environmental benefits on water quality and increasing capacity for flood waters. Research and investment into the production, use and distribution of biofuels. This will be necessary to reduce the environmental impact of existing diesel engines which, given their longevity, will still be around until well after 2050.
    [Show full text]
  • Waterway Dimensions
    Generated by waterscape.com Dimension Data The data published in this documentis British Waterways’ estimate of the dimensions of our waterways based upon local knowledge and expertise. Whilst British Waterways anticipates that this data is reasonably accurate, we cannot guarantee its precision. Therefore, this data should only be used as a helpful guide and you should always use your own judgement taking into account local circumstances at any particular time. Aire & Calder Navigation Goole to Leeds Lock tail - Bulholme Lock Length Beam Draught Headroom - 6.3m 2.74m - - 20.67ft 8.99ft - Castleford Lock is limiting due to the curvature of the lock chamber. Goole to Leeds Lock tail - Castleford Lock Length Beam Draught Headroom 61m - - - 200.13ft - - - Heck Road Bridge is now lower than Stubbs Bridge (investigations underway), which was previously limiting. A height of 3.6m at Heck should be seen as maximum at the crown during normal water level. Goole to Leeds Lock tail - Heck Road Bridge Length Beam Draught Headroom - - - 3.71m - - - 12.17ft - 1 - Generated by waterscape.com Leeds Lock tail to River Lock tail - Leeds Lock Length Beam Draught Headroom - 5.5m 2.68m - - 18.04ft 8.79ft - Pleasure craft dimensions showing small lock being limiting unless by prior arrangement to access full lock giving an extra 43m. Leeds Lock tail to River Lock tail - Crown Point Bridge Length Beam Draught Headroom - - - 3.62m - - - 11.88ft Crown Point Bridge at summer levels Wakefield Branch - Broadreach Lock Length Beam Draught Headroom - 5.55m 2.7m - - 18.21ft 8.86ft - Pleasure craft dimensions showing small lock being limiting unless by prior arrangement to access full lock giving an extra 43m.
    [Show full text]
  • Railways List
    A guide and list to a collection of Historic Railway Documents www.railarchive.org.uk to e mail click here December 2017 1 Since July 1971, this private collection of printed railway documents from pre grouping and pre nationalisation railway companies based in the UK; has sought to expand it‟s collection with the aim of obtaining a printed sample from each independent railway company which operated (or obtained it‟s act of parliament and started construction). There were over 1,500 such companies and to date the Rail Archive has sourced samples from over 800 of these companies. Early in 2001 the collection needed to be assessed for insurance purposes to identify a suitable premium. The premium cost was significant enough to warrant a more secure and sustainable future for the collection. In 2002 The Rail Archive was set up with the following objectives: secure an on-going future for the collection in a public institution reduce the insurance premium continue to add to the collection add a private collection of railway photographs from 1970‟s onwards provide a public access facility promote the collection ensure that the collection remains together in perpetuity where practical ensure that sufficient finances were in place to achieve to above objectives The archive is now retained by The Bodleian Library in Oxford to deliver the above objectives. This guide which gives details of paperwork in the collection and a list of railway companies from which material is wanted. The aim is to collect an item of printed paperwork from each UK railway company ever opened.
    [Show full text]
  • Source 12 AW.Indd
    Words Deborah Mulhearn Photographs Ian Lawson, Walter Menzies and courtesy British Waterways Cheshire’s beautiful and fascinating canals are at the forefront of the nation’s canal renaissance. Cheshire’s canals are perhaps the most diverse in the ago – to young and distinctly urban The Peak Forest Canal touches country. From the fascinating industrial heritage of the landlubbers are negotiating the locks. Boating Cheshire only briefl y, but has one of mighty Manchester Ship Canal, which cuts across the holiday companies are doing great business. its most spectacular features: the Northern edge of the county, to the dramatic Pennine The Cheshire Ring, a 97 mile long circular Marple Aqueduct and the fl ight of 16 scenery of the Macclesfi eld Canal in the east, and the route which is made up from parts of the locks that lift the canal 46m above serene beauty of the Llangollen Canal in the south-west Macclesfi eld Canal, the Peak Forest Canal, the Goyt Valley. The Trent & Mersey corner, they not only cover most of the county but also the Bridgewater Canal and the Trent & Mersey Canal, built to link the River Trent span the history of British canal building. Canal, has never been busier. and the River Mersey, was one of the Cheshire’s proximity to Liverpool and Manchester, “There’s a weird and wonderful mix of earliest canals to be completed, in the hub and heart of the industrial revolution, and to the features specifi c to Cheshire’s canals,” 1777. It runs for 92 miles and has River Mersey, meant that it was quickly criss-crossed explains Peter Birch of British Waterways even more locks – one section with by canals in the eighteenth and nineteenth centuries.
    [Show full text]
  • THE TUB BOAT Newsletter of the Bude Canal & Harbour Society
    THE TUB BOAT Newsletter of the Bude Canal & Harbour Society No. 58 Winter 2011 THE TUB BOAT Newsletter of the Bude Canal & Harbour Society No. 58 Winter 2011 CONTENTS Creaks from the Chair. 2 Membership Report . 3 Bude Canal Trust Report. 4 Your Society Needs You . 6 Future of the Higher Wharf . 7 Sherry and Mincepie event. 8 Producing 19th century boats in the 21st century . 8 Agnes. 9 Canal Recipes. .12 TRAC Photo Report. .. .15 Cover:The Bude Harbour and Breakwater Photo: Mike Moore 1 CREAKS FROM THE CHAIR A very happy and healthy new year to all our members and may 2012 bring achievements and satisfaction in as many of our ambitions and aspirations as one dare hope for. Here in Bude we continue to agitate for the unnecessarily elusive completion to the canal regeneration which would enable boats of a decent size to pass under Rodds Bridge and having done so, to continue unobstructed into the canal basin at Helebridge through the beautiful old canal bridge which carries the old A39 over both canal and river within a few yards of each other; it's a by-way these days but still much used by walkers. Our ambition for a slipway to enable such boats to access the canal in the first place is part of the ongoing campaign to save the site of Stapleton's shipyard from random development by Cornwall Council and become instead, a valuable waterside base for the gig and canoe clubs and an asset to Bude and Bude people. After some very wild and wet weather the canal is very full of water but the birds are all down the Bude end.
    [Show full text]
  • Directory of Resources
    SETTLE – CARLISLE RAILWAY DIRECTORY OF RESOURCES A listing of printed, audio-visual and other resources including museums, public exhibitions and heritage sites * * * Compiled by Nigel Mussett 2016 Petteril Bridge Junction CARLISLE SCOTBY River Eden CUMWHINTON COTEHILL Cotehill viaduct Dry Beck viaduct ARMATHWAITE Armathwaite viaduct Armathwaite tunnel Baron Wood tunnels 1 (south) & 2 (north) LAZONBY & KIRKOSWALD Lazonby tunnel Eden Lacy viaduct LITTLE SALKELD Little Salkeld viaduct + Cross Fell 2930 ft LANGWATHBY Waste Bank Culgaith tunnel CULGAITH Crowdundle viaduct NEWBIGGIN LONG MARTON Long Marton viaduct APPLEBY Ormside viaduct ORMSIDE Helm tunnel Griseburn viaduct Crosby Garrett viaduct CROSBY GARRETT Crosby Garrett tunnel Smardale viaduct KIRKBY STEPHEN Birkett tunnel Wild Boar Fell 2323 ft + Ais Gill viaduct Shotlock Hill tunnel Lunds viaduct Moorcock tunnel Dandry Mire viaduct Mossdale Head tunnel GARSDALE Appersett Gill viaduct Mossdale Gill viaduct HAWES Rise Hill tunnel DENT Arten Gill viaduct Blea Moor tunnel Dent Head viaduct Whernside 2415 ft + Ribblehead viaduct RIBBLEHEAD + Penyghent 2277 ft Ingleborough 2372 ft + HORTON IN RIBBLESDALE Little viaduct Ribble Bridge Sheriff Brow viaduct Taitlands tunnel Settle viaduct Marshfield viaduct SETTLE Settle Junction River Ribble © NJM 2016 Route map of the Settle—Carlisle Railway and the Hawes Branch GRADIENT PROFILE Gargrave to Carlisle After The Cumbrian Railways Association ’The Midland’s Settle & Carlisle Distance Diagrams’ 1992. CONTENTS Route map of the Settle-Carlisle Railway Gradient profile Introduction A. Primary Sources B. Books, pamphlets and leaflets C. Periodicals and articles D. Research Studies E. Maps F. Pictorial images: photographs, postcards, greetings cards, paintings and posters G. Audio-recordings: records, tapes and CDs H. Audio-visual recordings: films, videos and DVDs I.
    [Show full text]
  • Appendix E, Canal Inundation Mapping
    Nuneaton and Bedworth Borough Council Strategic Flood Risk Assessment - Level 2 Appendix E: Canal Inundation Mapping November 2012 Nuneaton and Bedworth Borough Council Town Hall Coton Road NUNEATON Warwickshire CV11 5AA This page is intentionally left blank Appendix e.doc I E Canal Inundation Mapping Appendix e.doc II Appendix e.doc III E.1 PDA2a: Scenario 1 Appendix e.doc IV Appendix e.doc V NOTES Canals do not generally pose a direct flood risk as they are a regulated water body. The residual risk from canals tends to be associated with lower probability events such as overtopping and embankment failure. As part of assessing flood risk from the canals, canal breach assessments have been identified based on areas of raised embankments in close proximity to proposed ¯ development sites. These assessments do not take the structural integrity of the embankment into account or quantify a risk of failure. Flooding may occur at any location along the canal system where there is a raised embankment. The mapping is intended to provide an indication of the likely impact of selected failure scenarios. It is not intended that inundation mapping provides a comprehensive analysis of all failure scenarios and further site specific analysis will need to be considered at all sites located within the vicinity of a canal system. Developers should be aware that any site that is at or below canal bank level may be subject to canal flooding and this should be taken into account when building resilience into low level properties Key Plan Legend Nuneaton and Bedworth Borough Depth (m) 0 - 0.01 Canal Breach Location Proposed Development Area 0.01 - 0.1 PDA2a 0.1 - 0.5 Principal watercourses 0.5 - 1.0 Other Watercourses 1.0 - 1.5 Coventry Canal 1.5 - 2.0 2.0 - 2.5 2.5 - 4.5 Reproduced from Ordnance Survey mapping with the permission of Ordnance Survey on behalf of the Controller of Her Majesty's Stationary Office.
    [Show full text]
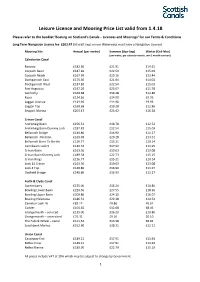
  • Leisure Licence and Mooring Price List Valid from 1.4.18
    Leisure Licence and Mooring Price List valid from 1.4.18 Please refer to the booklet ‘Boating on Scotland’s Canals – Licences and Moorings’ for our Terms & Conditions Long Term Navigation Licence fee £203.47 (All craft kept on our Waterways must have a Navigation Licence) Mooring Site Annual (per metre) Summer (Apr-Sep) Winter (Oct-Mar) (per metre, per calendar month, min 3 month contract) Caledonian Canal Banavie £182.60 £21.91 £14.61 Corpach Basin £187.82 £22.54 £15.03 Corpach Reach £167.99 £20.16 £13.44 Dochgarroch East £175.30 £21.04 £14.02 Dochgarroch West £187.82 £22.54 £15.03 Fort Augustus £197.20 £23.67 £15.78 Gairlochy £160.68 £19.28 £12.86 Kytra £124.16 £14.90 £9.93 Laggan Avenue £124.16 £14.90 £9.93 Laggan Top £160.68 £19.28 £12.86 Seaport Marina £203.47 £24.42 £16.28 Crinan Canal Ardrishaig Basin £156.51 £18.78 £12.52 Ardrishaig Basin Dummy Lock £187.82 £22.54 £15.03 Bellanoch Bridge £140.86 £16.90 £11.27 Bellanoch Pontoon £169.03 £20.28 £13.52 Bellanoch Stern To Berths £126.77 £15.21 £10.14 Cairnbaarn Lock 5 £149.32 £17.92 £11.95 Crinan Basin £163.56 £19.63 £13.08 Crinan Basin Dummy Lock £189.38 £22.73 £15.15 Crinan Rings £126.77 £15.21 £10.14 Lock 14 Crinan £163.56 £19.63 £13.08 Lock 4 Top £140.86 £16.90 £11.27 Oakfield Bridge £140.86 £16.90 £11.27 Forth & Clyde Canal Auchinstarry £135.00 £16.20 £10.80 Bowling Lower Basin £229.56 £27.55 £18.36 Bowling Upper Basin £200.86 £24.10 £16.07 Bowling Helenslea £186.51 £22.38 £14.92 Camelon Lock 16 £82.17 £9.86 £6.57 Cadder £105.65 £12.68 £8.45 Grangemouth – serviced £135.00 £16.20 £10.80 Grangemouth – unserviced £76.31 £9.16 £6.10 The Falkirk Wheel – canal £111.52 £13.38 £8.92 Southbank Marina £152.60 £18.31 £12.21 Union Canal Causeway End £149.21 £17.91 £11.94 Ratho linear £149.21 £17.91 £11.94 Ratho Marina £189.90 £22.79 £15.19 All prices include VAT at 20% which may be subject to change by Government.
    [Show full text]
  • Canals and Railways in the Industrial Revolution Tour | Tours for Seniors in Britain
    Australia 1300 888 225 New Zealand 0800 440 055 [email protected] From $13,995 AUD Single Room $15,995 AUD Twin Room $13,995 AUD Prices valid until 30th December 2021 23 days Duration England Destination Level 2 - Moderate Activity Canals and Railways in the Industrial Revolution Tour | Tours for Seniors in Britain Oct 05 2021 to Oct 27 2021 An Industrial Revolution Tour for Seniors | Exploring Britain’s history through its canals and railways This small group tour uncovers British history through the canals and railways of the Industrial Revolution. Learn how the Industrial Revolution brought significant and lasting change to Britain. Discover how engineers overcame geographical obstacles using viaducts, bridges, aqueducts, tunnels, and locks. Witness first hand the groundbreaking technology and the many impressive structures that transformed Canals and Railways in the Industrial Revolution Tour | Tours for Seniors in Britain 30-Sep-2021 1/15 https://www.odysseytraveller.com.au Australia 1300 888 225 New Zealand 0800 440 055 [email protected] Britain’s economy, some now restored for recreational purposes. However, our tour program is not only a study of the physical impact such a fundamental change made to world history. Led by local guides selected for their expertise, we also provide the opportunity to examine and discuss the resulting social upheaval. Packed to the brim with history, culture, and striking scenery, Great Britain and Ireland have a lot to offer the traveller. Our small group tour of the British isles are perfect for the mature or senior traveller who wants to explore the history of Britain and Ireland as part of an intimate guided tour with an expert local guide.
    [Show full text]