DOCSLIB.ORG

A Guide to Using PEST for Groundwater-Model Calibration

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Guide to Using PEST for Groundwater-Model Calibration Groundwater Resources Program Global Change Research & Development Approaches to Highly Parameterized Inversion: A Guide to Using PEST for Groundwater-Model Calibration Original image Singular values used: 1 Singular values used: 2 Singular values used: 3 Singular values used: 4 Singular values used: 5 Singular values used: 7 Singular values used: 20 Scientific Investigations Report 2010–5169 U.S. Department of the Interior U.S. Geological Survey Cover photo: Michael N. Fienen Approaches to Highly Parameterized Inversion: A Guide to Using PEST for Groundwater-Model Calibration By . John E Doherty and Randall J. Hunt Scientific Investigations Report 2010–5169 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior KEN SALAZAR, Secretary U.S. Geological Survey Marcia K. McNutt, Director U.S. Geological Survey, Reston, Virginia: 2010 For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment, visit http://www.usgs.gov or call 1-888-ASK-USGS For an overview of USGS information products, including maps, imagery, and publications, visit http://www.usgs.gov/pubprod To order this and other USGS information products, visit http://store.usgs.gov Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. Suggested citation: Doherty, J.E., and Hunt, R.J., 2010, Approaches to highly parameterized inversion—A guide to using PEST for groundwater-model calibration: U.S. Geological Survey Scientific Investigations Report 2010–5169, 59 p. iii Contents Abstract ...........................................................................................................................................................1 Introduction ....................................................................................................................................................1 Purpose and Scope .......................................................................................................................................2 Regularized Inversion ...................................................................................................................................2 Mathematical Regularization ..............................................................................................................3 Tikhonov Regularization .......................................................................................................................3 Subspace Regularization .....................................................................................................................4 A “Singularly Valuable Decomposition” —Benefits of SVD for Model Calibration ..........4 SVD-Assist and the Hybrid of Tikhonov and SVD ............................................................................6 Before Running PEST: Model Parameterization ......................................................................................6 Parameterization Philosophy ..............................................................................................................6 Spatial Parameterization .....................................................................................................................7 Zones of Piecewise Constancy .................................................................................................7 Pilot Points ....................................................................................................................................7 Conceptual Overview of Pilot-Point Use (excerpted from Doherty, Fienen, and Hunt, 2010)....................................................8 Pilot Points in Conjunction with Zones .....................................................................................9 Other Parameter Types ...............................................................................................................9 Initial Parameter Values ....................................................................................................................10 Tikhonov Regularization Strategies .................................................................................................10 Preferred-Value Regularization ...............................................................................................11 Preferred-Difference Regularization ......................................................................................11 Before Running PEST: Observations Used in Inversion Process ........................................................12 Formulation of an Objective Function ..............................................................................................12 Objective-Function Components ......................................................................................................12 Data of Different Types .............................................................................................................13 Special Considerations for Concentration Data ...................................................................13 Temporal Head Differences ......................................................................................................13 Vertical Interaquifer Head Differences ..................................................................................13 Joint Steady-State/Transient Calibration ...............................................................................14 Declustering ...............................................................................................................................14 Digital Filtering ...........................................................................................................................14 “Intuitive” and Other Soft Data .................................................................................................14 Temporal and Spatial Interpolation .........................................................................................14 A Note on Model Validation ..............................................................................................................15 Before Running PEST: Preparing the Run Files .......................................................................................15 Control Data .........................................................................................................................................15 Memory Conservation ...............................................................................................................15 The Marquardt Lambda .............................................................................................................15 Broyden’s Jacobian Update .....................................................................................................16 Number of Optimization Iterations ..........................................................................................16 Automatic User Intervention ....................................................................................................16 iv Solution Mechanism ..........................................................................................................................16 Parameter Groups ..............................................................................................................................17 Derivatives Calculation .............................................................................................................17 Regularization Considerations .................................................................................................17 Parameter Data ...................................................................................................................................18 Initial Parameter Values ...........................................................................................................18 Parameter Transformation .......................................................................................................18 Scale and Offset .........................................................................................................................18 Observation Groups ............................................................................................................................18 Objective-Function Contributions ...........................................................................................18 Weight Matrices ........................................................................................................................18 Regularization Groups ...............................................................................................................18 Observation Data ................................................................................................................................19 Model Command Line ........................................................................................................................19 Model Input/Output ............................................................................................................................19 Prior Information .................................................................................................................................19
Load more

Recommended publications
  • Hydrologic Processes Modeling Workshop Tucson, Arizona November 8-9, 2000
    Hydrologic Processes Modeling Workshop Tucson, Arizona November 8-9, 2000 ACKNOWLEDGEMENTS This Workshop on Hydrologic Process Modeling and the report you are reading would not have been possible without the efforts of many individuals. These people gave of themselves because they care about hydrologic modeling, their profession, and because they want to see technology used for better resource decision making. The concept to pursue this workshop would not have been possible without the support from the Subcommittee on Hydrology (SOH). The SOH in their foresight established the Task Committee on Hydrologic Modeling and allowed those members the freedom to organize and convene this workshop. Appreciation is extended to all members on the Task Committee on Hydrologic Modeling, which includes: Mimi Dannel; Russ Kinnerson, Arlen Feldman; Marshall Flug; Donald Frevert, Chair; Doug Glysson; George Leavesley; Steve Markstrom; Jayantha Obeysekera; Mike Smith; Ming Tseng; Don Woodward; and Ray Whittemore. In addition, the University of Arizona provided our host facility, arranged the logistical details for the workshop, and provided a great environment for this workshop. Special appreciation is extended to Paul Baltes for making the on site arrangements for the workshop and to Pam Lawler, for assisting Paul with the on-site arrangements and also handling the registration for this workshop. Soroosh Sorooshian, who initially agreed to get the UA involved as host facility, and Hoshin Gupta, both of SAHRA as well as Jim Washburne, Assistant Director for Education at the UA are owed our thanks for arranging and coordinating UA’s faculty, staff and student support of this workshop. Special thanks are extended to Terri Sue Hogue for scheduling and overseeing the students from the University of Arizona that served as note takers, recorders, and prepared the written Discussions for the four Panels and of the Breakout sessions.
    [Show full text]
  • Assessment of Groundwater Modeling Approaches for Brackish Aquifers
    Assessment of Groundwater Modeling Approaches for Brackish Aquifers Final Report Prepared by Neil E. Deeds, Ph.D., P.E. Toya L. Jones, P.G. Prepared for: Texas Water Development Board P.O. Box 13231, Capitol Station Austin, Texas 78711-3231 November 2011 Texas Water Development Board Assessment of Groundwater Modeling Approaches for Brackish Aquifers Final Report by Neil E. Deeds, Ph.D., P.E. Toya L. Jones, P.G. INTERA Incorporated November 2011 iii This page is intentionally blank. iv Table of Contents Executive Summary ........................................................................................................................ 1 1.0 Introduction ......................................................................................................................... 2 2.0 Literature Review................................................................................................................ 3 2.1 Importance of Variable Density on Flow and Transport ........................................... 3 2.1.1 Introduction to Mixed Convection Systems .................................................. 3 2.1.2 Describing the Degree of Mixed Convection ................................................ 4 2.1.3 Examples of Mixed Convection Systems ...................................................... 5 2.2 Codes that Simulate Variable Density Flow and Transport ....................................... 6 2.3 Brackish Water Hydrogeology ................................................................................ 19 2.4 Brackish Water
    [Show full text]
  • Supported Operating Environment
    Supported Operating Environment System Level Guides Current 9/28/2021 Table of Contents Supported Operating Environment Reference 5 Product List 8 Billing Data Server 10 Composer 12 CSTA Connector for BroadSoft BroadWorks 18 CX Contact 22 Decisions 26 eServices 29 Framework 49 Genesys Administrator Extension 72 Genesys Agent Scripting 80 Genesys Intelligent Automation (formerly GAAP) 84 Genesys Co-browse 88 Genesys Customer Experience Insights 92 Genesys Desktop 98 Genesys Info Mart 103 Genesys Interaction Recording 109 Genesys Interactive Insights 119 Genesys IVR SDK 127 Genesys Knowledge Center 131 Genesys Media Server 136 Genesys Mobile Services 146 Genesys Predictive Routing 151 Genesys Pulse 154 Genesys Quality Management (Zoom) 161 Genesys Rules System 164 Genesys Skills Management 171 Genesys Softphone 177 Genesys Video Gateway 182 Genesys Voice Platform 186 Genesys Voice Platform Studio 194 Genesys Voice Platform Voice Application Reporter 196 Genesys Web Engagement 199 Genesys WebRTC Service 204 Genesys Widgets 213 Gplus Adapter for Microsoft CRM 216 Gplus Adapter for SAP Analytics 218 Gplus Adapter for SAP CRM 222 Gplus Adapter for SAP Data Access Component 226 Gplus Adapter for SAP ERP 230 Gplus Adapter for SAP ICI Multi-Channel 234 Gplus Adapter for Siebel CRM 238 intelligent Workload Distribution 244 Interaction Concentrator 251 Interaction SDK 274 IVR Interface Option 281 License Reporting Manager 286 LivePerson Adapter 291 Load Distribution Server 295 Messaging Apps/Social Engagement 299 Multimedia Connector for Skype for
    [Show full text]
  • Application of MODFLOW with Boundary Conditions Analyses Based on Limited Available Observations: a Case Study of Birjand Plain in East Iran
    water Article Application of MODFLOW with Boundary Conditions Analyses Based on Limited Available Observations: A Case Study of Birjand Plain in East Iran Reza Aghlmand 1 and Ali Abbasi 1,2,* 1 Department of Civil Engineering, Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad 9177948974, Iran; [email protected] 2 Faculty of Civil Engineering and Geosciences, Water Resources Section, Delft University of Technology, Stevinweg 1, 2628 CN Delft, The Netherlands * Correspondence: [email protected] or [email protected]; Tel.: +31-15-2781029 Received: 18 July 2019; Accepted: 9 September 2019; Published: 12 September 2019 Abstract: Increasing water demands, especially in arid and semi-arid regions, continuously exacerbate groundwater resources as the only reliable water resources in these regions. Groundwater numerical modeling can be considered as an effective tool for sustainable management of limited available groundwater. This study aims to model the Birjand aquifer using GMS: MODFLOW groundwater flow modeling software to monitor the groundwater status in the Birjand region. Due to the lack of the reliable required data to run the model, the obtained data from the Regional Water Company of South Khorasan (RWCSK) are controlled using some published reports. To get practical results, the aquifer boundary conditions are improved in the established conceptual method by applying real/field conditions. To calibrate the model parameters, including the hydraulic conductivity, a semi-transient approach is applied by using the observed data of seven years. For model performance evaluation, mean error (ME), mean absolute error (MAE), and root mean square error (RMSE) are calculated. The results of the model are in good agreement with the observed data and therefore, the model can be used for studying the water level changes in the aquifer.
    [Show full text]
  • [1 ] Oracle Glassfish Server
    Oracle[1] GlassFish Server Release Notes Release 3.1.2 and 3.1.2.2 E24939-10 April 2015 These Release Notes provide late-breaking information about GlassFish Server 3.1.2 and 3.1.2.2 software and documentation. These Release Notes include summaries of supported hardware, operating environments, and JDK and JDBC/RDBMS requirements. Also included are a summary of new product features in the 3.1.2 and 3.1.2.2 releases, and descriptions and workarounds for known issues and limitations. Oracle GlassFish Server Release Notes, Release 3.1.2 and 3.1.2.2 E24939-10 Copyright © 2015, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs, including any operating system, integrated software, any programs installed on the hardware, and/or documentation, delivered to U.S.
    [Show full text]
  • GMS User Manual (V8.3) the Groundwater Modeling System
    GMS User Manual (v8.3) The Groundwater Modeling System PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Tue, 31 Jul 2012 20:55:45 UTC Contents Articles 1. Learning GMS 1 What is GMS? 1 The GMS Screen 1 Tool Palettes 4 Project Explorer 6 Tutorials 7 2. Set Up 8 64 bit 8 License Agreement 8 Registering GMS 9 Community Edition 10 Graphics Card Troubleshooting 11 Reporting Bugs 14 3. General Tools 15 3.1. The File Menu 16 The File Menu 16 3.2. The Edit Menu 17 The Edit Menu 17 Units 18 Preferences 19 Materials 23 Material Set 24 3.2.1. Coordinate Systems 25 Coordinate Systems 25 Coordinate Conversions 27 Projections 28 CPP Coordinate System 29 Geographic Coordinate System 30 Local Coordinate System 30 Coordinate Transformation 31 Transform 32 3.3. The Display Menu 33 The Display Menu 33 Contour Options 35 Animations 37 Color Ramp 39 3.3.1. Display Options 41 Display Options 41 Drawing Grid Options 42 Vectors 43 Lighting Options 44 Plot Axes 45 3.4. Other Tools 47 Annotations 47 CAD Options 51 Cross Sections 51 Data Sets 55 Data Calculator 58 Display Theme 60 XY Series Editor 61 4. Interpolation 62 4.1. Introduction 63 Interpolation 63 Interpolation Commands 64 3D Interpolation Options 65 Steady State vs. Transient Interpolation 66 4.2. Linear 67 Linear 67 4.3. Inverse Distance Weighted 68 Inverse Distance Weighted 68 Shepards Method 68 Gradient Plane Nodal Functions 69 Quadratic Nodal Functions 70 Subset Definition 71 Computation of Interpolation Weights 72 4.4.
    [Show full text]
  • Water Resource Software APPLICATION OVERVIEW and REVIEW Public Disclosure Authorized Public Disclosure Authorized
    APPLICATION OVERVIEW AND REVIEW Public Disclosure Authorized Water Resource Software APPLICATION OVERVIEW AND REVIEW Public Disclosure Authorized Public Disclosure Authorized By Carter Borden, Anju Gaur and Chabungbam R. Singh March 2016 Public Disclosure Authorized 1 Water Resource Software 2 APPLICATION OVERVIEW AND REVIEW Water Resource Software APPLICATION OVERVIEW AND REVIEW By Carter Borden, Anju Gaur and Chabungbam R. Singh March 2016 3 Water Resource Software Acknowledgements Many individuals and organization have supported this analysis. Specific contributions of note include water resources software developers Deltares, DHI, eWater, NIH, SEI, and USGS responded to a software questionnaire outlining the functionality and applications of their products. Individuals at the Government of India’s Central Water Commission and National Institute of Hydrology provided valuable comments on their experience of WRS applications in India. Kees Bons provided further clarification of the Deltares software functionality. Apruban Mukherjee and Anil Vyas provided additional information on USACE HEC software. Finally, Dr. Daniele Tonina provided a thorough and comprehensive review of the document. 4 APPLICATION OVERVIEW AND REVIEW OVERVIEW The National Hydrology Project (NHP) is an initiative by the Government of India’s Ministry of Water Resources and the World Bank to develop hydro-meteorological monitoring systems and provide scientifically-based tools and design aids to assist implementing agencies in the effective water resources planning
    [Show full text]
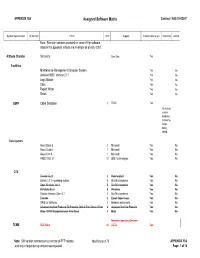
  • APPENDIX 13A Assigned Software Matrix Contract NAS 10-02007
    APPENDIX 13A Assigned Software Matrix Contract NAS 10-02007 System Nomenclature ID Number TITLE QTY Supplier Transferrable to gov Reference Limited Note: Revision numbers provided on some of the software listed in this appendix reflects the inventory as of early 2001. Altitude Chamber Simplicity Gen. Elec. Yes Facilities Maintenance Management Computer System Yes No Andover 9000 Version 2.17 Yes No Logic Master Yes No Citrix Yes No Report Writer Yea No Smart Yes No SSPF Cable Database 1 PGOC Yes No license, custom database. Cables no longer being added. Data Systems Visual Basic 6 2 Microsoft Yes No Visual Suite 6 1 Microsoft Yes No Visual C++ 6 1 Microsoft Yes No PASS 1000 3.7 12 SBS Technologies Yes No CITE Exceed v5.2.1 2 Hummingbird Yes No Solaris 1.0.1 - operating system 8 Sun Microsystems Yes No Open Windows Ver.3 8 Sun Microsystems Yes No VX Works 5.0.2 8 Windriver Yes No Solstice Network Client 3.1 2 Sun Microsystems Yes No Exocode 3 Expert Object Corp. Yes No GPIB for VxWorks 3 National Instruments Yes No Advanced Archival Products SQ Erasable Optical Disk Device Driver 6 Advanced Archival Products Yes No Milan TCP/IP Fastport network Print Serve 3 Milan Yes No Network Computing Devices TCMS PCX Ware 16 (NCD) Yes Note: SW version numbers are current as of RFP release Modification 173 APPENDIX 13A and may change during contract award period. Page: 1 of 16 APPENDIX 13A Assigned Software Matrix Contract NAS 10-02007 System Nomenclature ID Number TITLE QTY Supplier Transferrable to gov Reference Limited (Operations) TCMS 6.0 IRIX
    [Show full text]
  • An Overview of Commonly Used Groundwater Modelling Software
    ISSN: 2350-0328 International Journal of AdvancedResearch in Science, Engineering and Technology Vol. 6, Issue 1, January 2019 An Overview of Commonly Used Groundwater Modelling Software C. P. Kumar Scientist ‗G‘, National Institute of Hydrology, Roorkee – 247667, India ABSTRACT: A groundwater model is any computational method that represents an approximation of an underground water system. While groundwater models are, by definition, a simplification of a more complex reality, they have proven to be useful tools over several decades for addressing a range of groundwater problems and supporting the decision-making process. There are many different ground-water modelling codes available, each with their own capabilities, operational characteristics, and limitations. If modelling is considered for a project, it is important to determine if a particular code is appropriate for that project, or if a code exists that can perform the simulations required in the project. This article presents an overview of most commonly used groundwater modelling codes. KEY WORDS: Groundwater, Numerical Modelling, MODFLOW, FEFLOW, PEST. I. INTRODUCTION Groundwater systems are affected by natural processes and human activity, and require targeted and ongoing management to maintain the condition of groundwater resources within acceptable limits, while providing desired economic and social benefits. Groundwater management and policy decisions must be based on knowledge of the past and present behaviour of the groundwater system, the likely response to future changes and the understanding of the uncertainty in those responses. The location, timing and magnitude of hydrologic responses to natural or human-induced events depend on a wide range of factors — for example, the nature and duration of the event that is impacting groundwater, the subsurface properties and the connection with surface water features such as rivers and oceans.
    [Show full text]
  • GMS User Manual (V9.1) the Groundwater Modeling System
    GMS User Manual (v9.1) The Groundwater Modeling System PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Wed, 08 May 2013 16:51:22 UTC Contents Articles 1. Learning GMS 1 What is GMS? 1 The GMS Screen 3 Tool Palettes 6 Project Explorer 9 Tutorials 10 2. Set Up 11 64 bit 11 License Agreement 11 Registering GMS 12 Community Edition 13 Graphics Card Troubleshooting 14 Reporting Bugs 18 3. General Tools 19 3.1. The File Menu 20 The File Menu 20 3.2. The Edit Menu 22 The Edit Menu 22 Units 24 Preferences 24 Materials 29 Material Set 29 3.2.1. Coordinate Systems 31 Coordinate Systems 31 Coordinate Conversions 32 Projections 33 CPP Coordinate System 35 Geographic Coordinate System 35 Local Coordinate System 36 Coordinate Transformation 36 Transform 37 3.3. The Display Menu 39 The Display Menu 39 Contour Options 41 Animations 44 Color Ramp 46 3.3.1. Display Options 48 Display Options 48 Drawing Grid Options 49 Vectors 50 Lighting Options 51 Plot Axes 53 3.4. Other Tools 54 Annotations 54 CAD Options 58 Cross Sections 59 Data Sets 63 Data Calculator 66 Display Theme 68 XY Series Editor 69 4. Interpolation 70 4.1. Introduction 71 Interpolation 71 Interpolation Commands 72 3D Interpolation Options 73 Steady State vs. Transient Interpolation 74 4.2. Linear 75 Linear 75 4.3. Inverse Distance Weighted 76 Inverse Distance Weighted 76 Shepards Method 77 Gradient Plane Nodal Functions 78 Quadratic Nodal Functions 79 Subset Definition 80 Computation of Interpolation Weights 81 4.4.
    [Show full text]
  • Computer Applications for Hydrologic Analysis in Mining and Reclamation1
    Computer Applications for Hydrologic Analysis in Mining and Reclamation1 by Paul T. Behum, Jr. and Stephen C. Parsons2 Abstract: Since the mid-1980's, the Office of Surface Mining (OSM), in cooperation with State and Tribal coal regulatory and reclamation agencies, has employed a series of technical software tools, under the framework of a program known as the Technical Information Processing System (TIPS). The TIPS program also provides state-of-the-art technical workstations to our State and Tribal partners for use and administration of these software tools. Currently, UNIX-based workstations and software are being replaced by new workstations and servers operating Microsoft Windows NT. This has necessitated a re-evaluation of the technical software to bring legacy UNIX and DOS- based applications to an NT-platform standard. In 1999, a team of State and OSM scientists and engineers evaluated off-the-shelf hydrologic software. The functional areas covered by this review are: (1) aquifer test analyses: software used to evaluate aquifer parameters such as hydraulic conductivity, transmissivity, and storativity; (2) ground-water flow and contaminant transport modeling: application of aquifer parameter data and a U. S. Geological Survey-developed modeling code (MODFLOW) to a conceptual model of subsurface flow and transport conditions for evaluations of ground-water flow and contaminant transport; (3) watershed chemistry and storm runoff analysis: software for studying watershed surface-water quality and stonn/runoff characteristics in both small and large watersheds; ( 4) erosion and sedimentation/channel and impoundment design: supplements to the existing core TIPS software SEDCAD and SURVCADD; and (S) water chemistry analysis: hydrochemical software used for statistical and graphical analysis of both baseline and post-mining data.
    [Show full text]
  • Hydrologic Processes Modeling Workshop Tucson, Arizona November 8-9, 2000
    Hydrologic Processes Modeling Workshop Tucson, Arizona November 8-9, 2000 ACKNOWLEDGEMENTS This Workshop on Hydrologic Process Modeling and the report you are reading would not have been possible without the efforts of many individuals. These people gave of themselves because they care about hydrologic modeling, their profession, and because they want to see technology used for better resource decision making. The concept to pursue this workshop would not have been possible without the support from the Subcommittee on Hydrology (SOH). The SOH in their foresight established the Task Committee on Hydrologic Modeling and allowed those members the freedom to organize and convene this workshop. Appreciation is extended to all members on the Task Committee on Hydrologic Modeling, which includes: Mimi Dannel; Russ Kinnerson, Arlen Feldman; Marshall Flug; Donald Frevert, Chair; Doug Glysson; George Leavesley; Steve Markstrom; Jayantha Obeysekera; Mike Smith; Ming Tseng; Don Woodward; and Ray Whittemore. In addition, the University of Arizona provided our host facility, arranged the logistical details for the workshop, and provided a great environment for this workshop. Special appreciation is extended to Paul Baltes for making the on site arrangements for the workshop and to Pam Lawler, for assisting Paul with the on-site arrangements and also handling the registration for this workshop. Soroosh Sorooshian, who initially agreed to get the UA involved as host facility, and Hoshin Gupta, both of SAHRA as well as Jim Washburne, Assistant Director for Education at the UA are owed our thanks for arranging and coordinating UA’s faculty, staff and student support of this workshop. Special thanks are extended to Terri Sue Hogue for scheduling and overseeing the students from the University of Arizona that served as note takers, recorders, and prepared the written Discussions for the four Panels and of the Breakout sessions.
    [Show full text]