COMP251: Binary Search Trees, AVL Trees & AVL Sort
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Suffix Trees
This material takes about 1.5 hours. 1 Suffix Trees Gusfield: Algorithms on Strings, Trees, and Sequences. Weiner 73 “Linear Pattern-matching algorithms” IEEE conference on automata and switching theory McCreight 76 “A space-economical suffix tree construction algorithm” JACM 23(2) 1976 Chen and Seifras 85 “Efficient and Elegegant Suffix tree construction” in Apos- tolico/Galil Combninatorial Algorithms on Words Another “search” structure, dedicated to strings. Basic problem: match a “pattern” (of length m) to “text” (of length n) • goal: decide if a given string (“pattern”) is a substring of the text • possibly created by concatenating short ones, eg newspaper • application in IR, also computational bio (DNA seqs) • if pattern avilable first, can build DFA, run in time linear in text • if text available first, can build suffix tree, run in time linear in pattern. • applications in computational bio. First idea: binary tree on strings. Inefficient because run over pattern many times. • fractional cascading? • realize only need one character at each node! Tries: • used to store dictionary of strings • trees with children indexed by “alphabet” • time to search equal length of query string • insertion ditto. • optimal, since even hashing requires this time to hash. • but better, because no “hash function” computed. • space an issue: – using array increases stroage cost by |Σ| – using binary tree on alphabet increases search time by log |Σ| 1 – ok for “const alphabet” – if really fussy, could use hash-table at each node. • size in worst case: sum of word lengths (so pretty much solves “dictionary” problem. But what about substrings? • Relevance to DNA searches • idea: trie of all n2 substrings • equivalent to trie of all n suffixes. -

Balanced Trees Part One
Balanced Trees Part One Balanced Trees ● Balanced search trees are among the most useful and versatile data structures. ● Many programming languages ship with a balanced tree library. ● C++: std::map / std::set ● Java: TreeMap / TreeSet ● Many advanced data structures are layered on top of balanced trees. ● We’ll see several later in the quarter! Where We're Going ● B-Trees (Today) ● A simple type of balanced tree developed for block storage. ● Red/Black Trees (Today/Thursday) ● The canonical balanced binary search tree. ● Augmented Search Trees (Thursday) ● Adding extra information to balanced trees to supercharge the data structure. Outline for Today ● BST Review ● Refresher on basic BST concepts and runtimes. ● Overview of Red/Black Trees ● What we're building toward. ● B-Trees and 2-3-4 Trees ● Simple balanced trees, in depth. ● Intuiting Red/Black Trees ● A much better feel for red/black trees. A Quick BST Review Binary Search Trees ● A binary search tree is a binary tree with 9 the following properties: 5 13 ● Each node in the BST stores a key, and 1 6 10 14 optionally, some auxiliary information. 3 7 11 15 ● The key of every node in a BST is strictly greater than all keys 2 4 8 12 to its left and strictly smaller than all keys to its right. Binary Search Trees ● The height of a binary search tree is the 9 length of the longest path from the root to a 5 13 leaf, measured in the number of edges. 1 6 10 14 ● A tree with one node has height 0. -
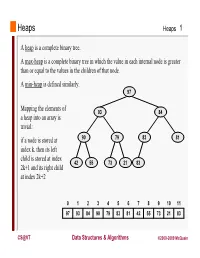
Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

CSCI 333 Data Structures Binary Trees Binary Tree Example Full And
Notes with the dark blue background CSCI 333 were prepared by the textbook author Data Structures Clifford A. Shaffer Chapter 5 Department of Computer Science 18, 20, 23, and 25 September 2002 Virginia Tech Copyright © 2000, 2001 Binary Trees Binary Tree Example A binary tree is made up of a finite set of Notation: Node, nodes that is either empty or consists of a children, edge, node called the root together with two parent, ancestor, binary trees, called the left and right descendant, path, subtrees, which are disjoint from each depth, height, level, other and from the root. leaf node, internal node, subtree. Full and Complete Binary Trees Full Binary Tree Theorem (1) Full binary tree: Each node is either a leaf or Theorem: The number of leaves in a non-empty internal node with exactly two non-empty children. full binary tree is one more than the number of internal nodes. Complete binary tree: If the height of the tree is d, then all leaves except possibly level d are Proof (by Mathematical Induction): completely full. The bottom level has all nodes to the left side. Base case: A full binary tree with 1 internal node must have two leaf nodes. Induction Hypothesis: Assume any full binary tree T containing n-1 internal nodes has n leaves. 1 Full Binary Tree Theorem (2) Full Binary Tree Corollary Induction Step: Given tree T with n internal Theorem: The number of null pointers in a nodes, pick internal node I with two leaf children. non-empty tree is one more than the Remove I’s children, call resulting tree T’. -

Tree Structures
Tree Structures Definitions: o A tree is a connected acyclic graph. o A disconnected acyclic graph is called a forest o A tree is a connected digraph with these properties: . There is exactly one node (Root) with in-degree=0 . All other nodes have in-degree=1 . A leaf is a node with out-degree=0 . There is exactly one path from the root to any leaf o The degree of a tree is the maximum out-degree of the nodes in the tree. o If (X,Y) is a path: X is an ancestor of Y, and Y is a descendant of X. Root X Y CSci 1112 – Algorithms and Data Structures, A. Bellaachia Page 1 Level of a node: Level 0 or 1 1 or 2 2 or 3 3 or 4 Height or depth: o The depth of a node is the number of edges from the root to the node. o The root node has depth zero o The height of a node is the number of edges from the node to the deepest leaf. o The height of a tree is a height of the root. o The height of the root is the height of the tree o Leaf nodes have height zero o A tree with only a single node (hence both a root and leaf) has depth and height zero. o An empty tree (tree with no nodes) has depth and height −1. o It is the maximum level of any node in the tree. CSci 1112 – Algorithms and Data Structures, A. -

Binary Search Tree
ADT Binary Search Tree! Ellen Walker! CPSC 201 Data Structures! Hiram College! Binary Search Tree! •" Value-based storage of information! –" Data is stored in order! –" Data can be retrieved by value efficiently! •" Is a binary tree! –" Everything in left subtree is < root! –" Everything in right subtree is >root! –" Both left and right subtrees are also BST#s! Operations on BST! •" Some can be inherited from binary tree! –" Constructor (for empty tree)! –" Inorder, Preorder, and Postorder traversal! •" Some must be defined ! –" Insert item! –" Delete item! –" Retrieve item! The Node<E> Class! •" Just as for a linked list, a node consists of a data part and links to successor nodes! •" The data part is a reference to type E! •" A binary tree node must have links to both its left and right subtrees! The BinaryTree<E> Class! The BinaryTree<E> Class (continued)! Overview of a Binary Search Tree! •" Binary search tree definition! –" A set of nodes T is a binary search tree if either of the following is true! •" T is empty! •" Its root has two subtrees such that each is a binary search tree and the value in the root is greater than all values of the left subtree but less than all values in the right subtree! Overview of a Binary Search Tree (continued)! Searching a Binary Tree! Class TreeSet and Interface Search Tree! BinarySearchTree Class! BST Algorithms! •" Search! •" Insert! •" Delete! •" Print values in order! –" We already know this, it#s inorder traversal! –" That#s why it#s called “in order”! Searching the Binary Tree! •" If the tree is -

Suffix Trees and Suffix Arrays in Primary and Secondary Storage Pang Ko Iowa State University
Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 2007 Suffix trees and suffix arrays in primary and secondary storage Pang Ko Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Bioinformatics Commons, and the Computer Sciences Commons Recommended Citation Ko, Pang, "Suffix trees and suffix arrays in primary and secondary storage" (2007). Retrospective Theses and Dissertations. 15942. https://lib.dr.iastate.edu/rtd/15942 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Suffix trees and suffix arrays in primary and secondary storage by Pang Ko A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Computer Engineering Program of Study Committee: Srinivas Aluru, Major Professor David Fern´andez-Baca Suraj Kothari Patrick Schnable Srikanta Tirthapura Iowa State University Ames, Iowa 2007 UMI Number: 3274885 UMI Microform 3274885 Copyright 2007 by ProQuest Information and Learning Company. All rights reserved. This microform edition is protected against unauthorized copying under Title 17, United States Code. ProQuest Information and Learning Company 300 North Zeeb Road P.O. Box 1346 Ann Arbor, MI 48106-1346 ii DEDICATION To my parents iii TABLE OF CONTENTS LISTOFTABLES ................................... v LISTOFFIGURES .................................. vi ACKNOWLEDGEMENTS. .. .. .. .. .. .. .. .. .. ... .. .. .. .. vii ABSTRACT....................................... viii CHAPTER1. INTRODUCTION . 1 1.1 SuffixArrayinMainMemory . -

Binary Tree Fall 2017 Stony Brook University Instructor: Shebuti Rayana [email protected] Introduction to Tree
CSE 230 Intermediate Programming in C and C++ Binary Tree Fall 2017 Stony Brook University Instructor: Shebuti Rayana [email protected] Introduction to Tree ■ Tree is a non-linear data structure which is a collection of data (Node) organized in hierarchical structure. ■ In tree data structure, every individual element is called as Node. Node stores – the actual data of that particular element and – link to next element in hierarchical structure. Tree with 11 nodes and 10 edges Shebuti Rayana (CS, Stony Brook University) 2 Tree Terminology ■ Root ■ In a tree data structure, the first node is called as Root Node. Every tree must have root node. In any tree, there must be only one root node. Root node does not have any parent. (same as head in a LinkedList). Here, A is the Root node Shebuti Rayana (CS, Stony Brook University) 3 Tree Terminology ■ Edge ■ The connecting link between any two nodes is called an Edge. In a tree with 'N' number of nodes there will be a maximum of 'N-1' number of edges. Edge is the connecting link between the two nodes Shebuti Rayana (CS, Stony Brook University) 4 Tree Terminology ■ Parent ■ The node which is predecessor of any node is called as Parent Node. The node which has branch from it to any other node is called as parent node. Parent node can also be defined as "The node which has child / children". Here, A is Parent of B and C B is Parent of D, E and F C is the Parent of G and H Shebuti Rayana (CS, Stony Brook University) 5 Tree Terminology ■ Child ■ The node which is descendant of any node is called as CHILD Node. -

Section 11.1 Introduction to Trees Definition
Section 11.1 Introduction to Trees Definition: A tree is a connected undirected graph with no simple circuits. : A circuit is a path of length >=1 that begins and ends a the same vertex. d d Tournament Trees A common form of tree used in everyday life is the tournament tree, used to describe the outcome of a series of games, such as a tennis tournament. Alice Antonia Alice Anita Alice Abigail Abigail Alice Amy Agnes Agnes Angela Angela Angela Audrey A Family Tree Much of the tree terminology derives from family trees. Gaea Ocean Cronus Phoebe Zeus Poseidon Demeter Pluto Leto Iapetus Persephone Apollo Atlas Prometheus Ancestor Tree An inverted family tree. Important point - it is a binary tree. Iphigenia Clytemnestra Agamemnon Leda Tyndareus Aerope Atreus Catreus Forest Graphs containing no simple circuits that are not connected, but each connected component is a tree. Theorem An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices. Rooted Trees Once a vertex of a tree has been designated as the root of the tree, it is possible to assign direction to each of the edges. Rooted Trees g a e f e c b b d a d c g f root node a internal vertex parent of g b c d e f g leaf siblings h i a b c d e f g h i h i ancestors of and a b c d e f g subtree with b as its h i root subtree with c as its root m-ary trees A rooted tree is called an m-ary tree if every internal vertex has no more than m children. -

Binary Trees
Binary Trees Chapter 12 Fundamentals • A binary tree is a nonlinear data structure. • A binary tree is either empty or it contains a root node and left- and right- subtrees that are also binary trees. • Applications: encryption, databases, expert systems Tree Terminology root A parent left-child right-child B C siblings leaf D E F G right-subtree left-subtree More Terminology • Consider two nodes in a tree, X and Y. • X is an ancestor of Y if X is the parent of Y, or X is the ancestor of the parent of Y. It’s RECURSIVE! • Y is a descendant of X if Y is a child of X, or Y is the descendant of a child of X. More Terminology • Consider a node Y. • The depth of a node Y is 0, if the Y is the root, or 1 + the depth of the parent of Y • The depth of a tree is the maximum depth of all its leaves. More Terminology • A full binary tree is a binary tree such that - all leaves have the same depth, and - every non-leaf node has 2 children. • A complete binary tree is a binary tree such that - every level of the tree has the maximum number of nodes possible except possibly the deepest level. - at the deepest level, the nodes are as far left as possible. Tree Examples 1 2 3 4 5 A A A A A B C B B B C D E F G D E A full binary tree is always a complete binary tree. -

Binary Search Trees! – These Are "Nonlinear" Implementations of the ADT Table
Data Structures Topic #8 Today’s Agenda • Continue Discussing Table Abstractions • But, this time, let’s talk about them in terms of new non-linear data structures – trees – which require that our data be organized in a hierarchical fashion Tree Introduction • Remember when we learned about tables? – We found that none of the methods for implementing tables was really adequate. – With many applications, table operations end up not being as efficient as necessary. – We found that hashing is good for retrieval, but doesn't help if our goal is also to obtain a sorted list of information. Tree Introduction • We found that the binary search also allows for fast retrieval, – but is limited to array implementations versus linked list. – Because of this, we need to move to more sophisticated implementations of tables, using binary search trees! – These are "nonlinear" implementations of the ADT table. Tree Terminology • Trees are used to represent the relationship between data items. – All trees are hierarchical in nature which means there is a parent-child relationship between "nodes" in a tree. – The lines between nodes are called directed edges. – If there is a directed edge from node A to node B -- then A is the parent of B and B is a child of A. Tree Terminology • Children of the same parent are called siblings. • Each node in a tree has at most one parent, starting at the top with the root node (which has no parent). • Parent of n The node directly above node n in the tree • Child of n The node directly below the node n in the tree Tree -

Balanced Binary Search Trees – AVL Trees, 2-3 Trees, B-Trees
Balanced binary search trees – AVL trees, 2‐3 trees, B‐trees Professor Clark F. Olson (with edits by Carol Zander) AVL trees One potential problem with an ordinary binary search tree is that it can have a height that is O(n), where n is the number of items stored in the tree. This occurs when the items are inserted in (nearly) sorted order. We can fix this problem if we can enforce that the tree remains balanced while still inserting and deleting items in O(log n) time. The first (and simplest) data structure to be discovered for which this could be achieved is the AVL tree, which is names after the two Russians who discovered them, Georgy Adelson‐Velskii and Yevgeniy Landis. It takes longer (on average) to insert and delete in an AVL tree, since the tree must remain balanced, but it is faster (on average) to retrieve. An AVL tree must have the following properties: • It is a binary search tree. • For each node in the tree, the height of the left subtree and the height of the right subtree differ by at most one (the balance property). The height of each node is stored in the node to facilitate determining whether this is the case. The height of an AVL tree is logarithmic in the number of nodes. This allows insert/delete/retrieve to all be performed in O(log n) time. Here is an example of an AVL tree: 18 3 37 2 11 25 40 1 8 13 42 6 10 15 Inserting 0 or 5 or 16 or 43 would result in an unbalanced tree.