Towards Brain-Scale Modelling of the Human Cerebral Blood Flow: Hybrid Approach and High Performance Computing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Name: Ezenwigbo Johnpaul Oluchukwu College
NAME: EZENWIGBO JOHNPAUL OLUCHUKWU COLLEGE: MEDICINE AND HEALTH SCIENCES DEPARTMENT: MEDICINE AND SURGERY MATRICULATION NUMBER: 18/MHS01/157 COURSE: PHYSIOLOGY LEVEL: 200 LEVEL ASSIGNMENT 1. Discuss the long-term regulation of mean arterial blood pressure? LONG-TERM REGULATION OF MEAN ARTERIAL BLOOD PRESSURE Kidneys play an important role in the long•term regulation of arterial blood pressure. When blood pressure alters slowly in several days/months/years, the nervous mechanism adapts to the altered pressure and loses the sensitivity for the changes. It cannot regulate the pressure any more. In such conditions, the renal mechanism operates efficiently to regulate the blood pressure. Therefore, it is called long•term regulation. Kidneys regulate arterial blood pressure by two ways: A. By regulation of extracellular fluid (ECF) volume B. Through renin•angiotensin mechanism. A. REGULATION OF EXTRACELLULAR FLUID VOLUME: When the blood pressure increases, kidneys excrete large amounts of water and salt, particularly sodium, by means of pressure diuresis and pressure natriuresis. Pressure diuresis is the excretion of large quantity of water in urine because of increased blood pressure. Even a slight increase in blood pressure doubles the water excretion. Pressure natriuresis is the excretion of large quantity of sodium in urine. Because of diuresis and natriuresis, there is a decrease in ECF volume and blood volume, which in turn brings the arterial blood pressure back to normal level. When blood pressure decreases, the reabsorption of water from renal tubules is increased. This in turn, increases ECF volume, blood volume and cardiac output, resulting in restoration of blood pressure. B. THROUGH RENIN-ANGIOTENSIN MECHANISM: When blood pressure and ECF volume decrease, renin secretion from kidneys is increased. -

7Th & 8 March-2016- Papers of All Specialties (1705 MCQS)
1 7th & 8th March-2016- Papers of all Specialties (1705 MCQS) [ Index- Check List ] Compiled by : Amlodipine Besylate (1) Medicine & Allied 7th March 2016 (Evening Session) by Alizay Khan (181 MCQS) Page#1 (2) Medice & Allied 8th March 2016 (Morning Session) by Dr Kunza Aslam (200 MCQS) P#15 (3) Medicine 8th March(Evening) by Dr.Tariq Khan/Mudassir Bangash (200MCQS) P#29 (4).Surgery & Allied 7th March (Evening Session) by Dr. Hasnain Afzal (197 MCQS) P#40 (5). Surgery & Allied 7th March (Evening Session) - by Dr.Xaheer Khan (185 MCQS) P#57 (6). Surgery 7th March 2016 (Morning Session) by By Dr.Haris Riaz Sheikh (156+) P#73 (7). Gyane/Obs 7th March-2016 (Morning Session) by Dr.Noor Fatima (184) P#89 (8)..Gynae / Obs; 8th March 2016 (Morning Session) Dr.Nourin Hameed (105) P#94 (9). Radiology 7th March-2016(Morning) by Dr.Asfandyar Khan Bhittani & Loa Loa(122) P#103 (10). Community Medicine 7th March 2016 (Morning) by Dr.Qaisar Javed (90+85) P#112 =-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= (1)Medicine & Allied 7th March 2016(evening) by Alizay Khan (181) 1. anterior cruciate ligament is damaged.direction of tibial dislocation on femur is a. anteriolateral b. anteromeddiaal c. anterior (answer) d. posterromedial e. posterolateral 2. narrowest point in pediatric airway a. cricoid (answer) b. thyroid c. trachea d. false vocal cord e. true vocal cords 3. regarding vertebral column a. intervertebral disc is thickest in thoracic and lumber regions b. cervical vertebrae are 7(answer) c. total 31 vertebrae d. curvature to side is caalled lordosis e. prolapse can occur without fracutre 4. -

Skeleton-Vasculature Chain Reaction: a Novel Insight Into the Mystery of Homeostasis
Bone Research www.nature.com/boneres REVIEW ARTICLE OPEN Skeleton-vasculature chain reaction: a novel insight into the mystery of homeostasis Ming Chen1,2,YiLi1,2, Xiang Huang1,2,YaGu1,2, Shang Li1,2, Pengbin Yin 1,2, Licheng Zhang1,2 and Peifu Tang 1,2 Angiogenesis and osteogenesis are coupled. However, the cellular and molecular regulation of these processes remains to be further investigated. Both tissues have recently been recognized as endocrine organs, which has stimulated research interest in the screening and functional identification of novel paracrine factors from both tissues. This review aims to elaborate on the novelty and significance of endocrine regulatory loops between bone and the vasculature. In addition, research progress related to the bone vasculature, vessel-related skeletal diseases, pathological conditions, and angiogenesis-targeted therapeutic strategies are also summarized. With respect to future perspectives, new techniques such as single-cell sequencing, which can be used to show the cellular diversity and plasticity of both tissues, are facilitating progress in this field. Moreover, extracellular vesicle-mediated nuclear acid communication deserves further investigation. In conclusion, a deeper understanding of the cellular and molecular regulation of angiogenesis and osteogenesis coupling may offer an opportunity to identify new therapeutic targets. Bone Research (2021) ;9:21 https://doi.org/10.1038/s41413-021-00138-0 1234567890();,: INTRODUCTION cells, pericytes, etc.) secrete angiocrine factors to modulate -
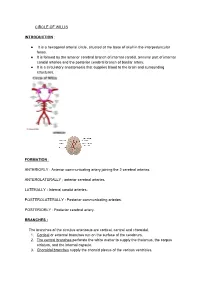
CIRCLE of WILLIS INTRODUCTION: It Is a Hexagonal
CIRCLE OF WILLIS INTRODUCTION : ● It is a hexagonal arterial circle, situated at the base of skull in the interpeduncular fossa. ● It is formed by the anterior cerebral branch of internal carotid, terminal part of internal carotid arteries and the posterior cerebral branch of basilar artery. ● It is a circulatory anastomosis that supplies blood to the brain and surrounding structures. FORMATION : ANTERIORLY : Anterior communicating artery joining the 2 cerebral arteries. ANTEROLATERALLY : anterior cerebral arteries. LATERALLY : Internal carotid arteries. POSTEROLATERALLY : Posterior communicating arteries. POSTERIORLY : Posterior cerebral artery. BRANCHES : The branches of the circulus arteriosus are cortical, central and choroidal. 1. Cortical or external branches run on the surface of the cerebrum. 2. The central branches perforate the white matter to supply the thalamus, the corpus striatum, and the internal capsule. 3. Choroidal branches supply the choroid plexus of the various ventricles. CORTICAL BRANCHES : These branches arise from all three cerebral arteries: ● Anterior cerebral ● Middle cerebral ● Posterior cerebral. 1. MIDDLE CEREBRAL ARTERY : It is the direct branch of internal carotid artery. CORTICAL BRANCHES : ● orbital ● Frontal ● Parietal ● Temporal. 2. ANTERIOR CEREBRAL ARTERY : It Is the smallest terminal branch of internal carotid artery. CORTICAL BRANCHES : ● Orbital ● Frontal ● Parietal. 3. POSTERIOR CEREBRAL : It is the terminal branch of basilar artery. CORTICAL BRANCHES : ● Temporal ● Occipital ● Parieto occipital. CEREBRAL CORTEX : Cerebral cortex is supplied by all the 3 arteries. ● SUPEROLATERAL SURFACE : This surface is mainly supplied by middle cerebral artery. ● MEDICAL AND TENTORIAL SURFACE : This surface is supplied by anterior cerebral artery. ● INFERIOR : Medial one third of orbital surface is supplied by anterior cerebral. Lateral two third, including the Temporal pole area and anterior surface of the Temporal pole is vascularised by middle cerebral artery. -

Physiology As
NAME: OKE ANUOLUWAPO ENIOLA MATRIC NUMBER: 18/MHS01/262 LEVEL: 200 LEVEL DEPARTMENT: MEDICINE AND SURGERY COURSE: PHYSIOLOGY ASSIGNMENT: 1) DISSCUSS THE LONG TERM REGULATION OF MEAN ARTERIAL BLOOD PRESSURE 2) WRITE SHORT NOTES ON A) PULMONARY CIRCULATION B) CIRCLE OF WILLIS C) SPLANCHNIC CIRCULATION D) CORONARY CIRCULATIOM E) CUTANEOUS CIRCULATION 3) DISCUSS THE CARDIOVASCULAR ADJUSTMENT THAT OCCURS DURING EXERCISE 1) DISCUSS THE LONG-TERM REGULATION OF MEAN ARTERIAL BLOOD RESSURE Arterial blood pressure varies even under physiological conditions. However, it’s immediately brought back to normal level because of the presence of well- organized regulatory mechanisms in the body. One of those mechanisms is the long term regulatory mechanism (renal mechanism). LONG TERM REGULATORY MECHANISM (RENAL MECHANISM) Consistent and long term control of blood-pressure is determined by the renin- angiotensin system. Along with vessel morphology, blood viscosity is one of the key main factors influencing resistance and hence blood pressure. A key modulator of blood pressure is the Renin-Angiotensin System (RAS) or the renin Angiotensin-Aldosterone System (RAAS), a hormone system that regulates blood pressure and water balance. When the volume of blood is low, juxtaglomerular cells in the kidney secrete renin directly into circulation. Plasma renin then carries out the conversion of angiotensinogen released by the liver to angiotensin I. Angiotensin I is subsequently converted to angiotensin II by the enzyme found in the lungs. Angiotensin II is a potent vasoactive peptide that causes blood vessels to constrict, resulting in increased blood pressure. Angiotensin II also stimulates the secretion of the hormone aldosterone from the adrenal cortex. -

A Perfusion Procedure for Imaging of the Mouse Cerebral Vasculature by X-Ray Micro-CT
Journal of Neuroscience Methods 221 (2014) 70–77 Contents lists available at ScienceDirect Journal of Neuroscience Methods jou rnal homepage: www.elsevier.com/locate/jneumeth Basic Neuroscience A perfusion procedure for imaging of the mouse cerebral vasculature by X-ray micro-CT a,b,∗ b a,b a,b Sahar Ghanavati , Lisa X. Yu , Jason P. Lerch , John G. Sled a Department of Medical Biophysics, University of Toronto, Toronto, Ontario, Canada M5G 2M9 b Mouse Imaging Centre, The Hospital for Sick Children, 25 Orde Street, Toronto, Ontario, Canada M5T 3H7 h i g h l i g h t s • Brain samples perfused with contrast agent have high inconsistency in the filling of the posterior cerebral circulation. • We revised the Microfil perfusion protocol, in order to reduce the variability of the outcome in samples. • The Microfil is first perfused through the posterior circulation by blocking the flow to the anterior circulation. • A workflow is provided to verify the successful completion of each surgical step. • The cerebellum shows 6.9%, and the midbrain about 8.7% increase in the percentage of vessel segments. a r t i c l e i n f o a b s t r a c t Article history: Background: Micro-CT is a novel X-ray imaging modality which can provide 3D high resolution images Received 12 July 2013 of the vascular network filled with contrast agent. The cerebrovascular system is a complex anatomical Received in revised form 26 August 2013 structure that can be imaged with contrast enhanced micro-CT. However, the morphology of the cere- Accepted 2 September 2013 brovasculature and many circulatory anastomosis in the brain result in high variations in the extent of contrast agent filling in the blood vessels and as a result, the vasculature of different subjects appear Keywords: differently in the acquired images. -

Is There a Connection Between Sublingual Varices and Hypertension? Lennart Hedström1*, Margit Albrektsson1 and Håkan Bergh2
Hedström et al. BMC Oral Health (2015) 15:78 DOI 10.1186/s12903-015-0054-2 RESEARCH ARTICLE Open Access Is there a connection between sublingual varices and hypertension? Lennart Hedström1*, Margit Albrektsson1 and Håkan Bergh2 Abstract Background: Sublingual varices have earlier been related to ageing, smoking and cardiovascular disease. The aim of this study was to investigate whether sublingual varices are related to presence of hypertension. Methods: In an observational clinical study among 431 dental patients tongue status and blood pressure were documented. Digital photographs of the lateral borders of the tongue for grading of sublingual varices were taken, and blood pressure was measured. Those patients without previous diagnosis of hypertension and with a noted blood pressure ≥ 140 mmHg and/or ≥ 90 mmHg at the dental clinic performed complementary home blood pressure during one week. Those with an average home blood pressure ≥135 mmHg and/or ≥85 mmHg were referred to the primary health care centre, where three office blood pressure measurements were taken with one week intervals. Two independent blinded observers studied the photographs of the tongues. Each photograph was graded as none/few (grade 0) or medium/severe (grade 1) presence of sublingual varices. Pearson’s Chi-square test, Student’s t-test, and multiple regression analysis were applied. Power calculation stipulated a study population of 323 patients. Results: An association between sublingual varices and hypertension was found (OR = 2.25, p < 0.002). Mean systolic blood pressure was 123 and 132 mmHg in patients with grade 0 and grade 1 sublingual varices, respectively (p < 0.0001, CI 95 %). -

Components of Circulatory System- Blood Vessels by Dr. Istiak Mahfuz
1 2 3 4 The arteries and veins have three layers, but the middle layer is thicker in the arteries than it is in the veins: Tunica intima (the thinnest layer): a single layer of simple squamous endothelial cells glued by a polysaccharide intercellular matrix, surrounded by a thin layer of subendothelial connective tissue interlaced with a number of circularly arranged elastic bands called the internal elastic lamina. Tunica media (the thickest layer in arteries): circularly arranged elastic fiber, connective tissue, polysaccharide substances, the second and third layer are separated by another thick elastic band called external elastic lamina. The tunica media may (especially in arteries) be rich in vascular smooth muscle, which controls the caliber of the vessel. Tunica adventitia: (the thickest layer in veins) entirely made of connective tissue. It also contains nerves that supply the vessel as well as nutrient capillaries (vasa vasorum) in the larger blood vessels. 5 The chief difference between arteries and veins is the job that they do. Arteries carry oxygenated blood away from the heart to the body, and veins carry oxygen-poor blood back from the body to the heart. Your body also contains other, smaller blood vessels. Major differences are 1, 3, 4, 5, 8 6 7 8 9 10 11 Capillary action (sometimes capillarity, capillary motion, or wicking) is the ability of a liquid to flow in narrow spaces without the assistance of, and in opposition to, external forces like gravity. 12 13 A Metarteriole (or arterial capillary[citation needed]) is a short vessel that links arterioles and venules.[1] Instead of a continuous tunica media, they have individual smooth muscle cells placed a short distance apart, each forming a precapillary sphincter that encircles the entrance to that capillary bed. -

1.In the Cardiovascular System, Blood Flow Is Controlled by Arterial Blood
1.In the cardiovascular system, blood flow is controlled by arterial blood pressure, and in this way the long- term mean blood pressure is stabilized to regulate oxygen and carbon dioxide levels. Thereafter, the baroreflex would stabilize the instantaneous pressure value to the prevailing carotid pressure (MAP). Changes in blood volume affect arterial pressure by changing cardiac output. An increase in blood volume increases central venous pressure. 2.Pulmonary circulation: The pulmonary circulation is the portion of the circulatory system which carries deoxygenated blood away from the right ventricle, to the lungs, and returns oxygenated blood to the left atrium and ventricle of the heart. The term pulmonary circulation is readily paired and contrasted with the systemic circulation. The vessels of the pulmonary circulation are the pulmonary arteries and the pulmonary veins. Circle of Willis : The circle of Willis (also called Willis' circle, loop of Willis, cerebral arterial circle, and Willis polygon) is a circulatory anastomosis that supplies blood to the brain and surrounding structures. It is named after Thomas Willis (1621–1675), an English physician. Splanchnic circulation: The term 'splanchnic circulation' describes the blood flow to the abdominal gastrointestinal organs including the stomach, liver, spleen, pancreas, small intestine, and large intestine. Coronary circulation :Coronary circulation is the circulation of blood in the blood vessels that supply the heart muscle (myocardium). Coronary arteries supply oxygenated blood to the heart muscle, and cardiac veins drain away the blood once it has been deoxygenated. Because the rest of the body, and most especially the brain, needs a steady supply of oxygenated blood that is free of all but the slightest interruptions, the heart is required to function continuously. -

Computational Hemodynamics of Cerebral Vasculature
POLITECNICO DI MILANO Dipartimento di Matematica F. Brioschi Ph. D. course in Mathematical Engineering XXI cycle Computational hemodynamics of the cerebral circulation: multiscale modeling from the circle of Willis to cerebral aneurysms Ph. D. candidate: Tiziano PASSERINI Milano, 2009 Supervisor: Prof. Alessandro VENEZIANI To Lucia Contents Abstract 1 1 Introduction 3 1.1 Anatomy and physiology of the cerebral circulation . 3 1.1.1 The circle of Willis . 4 1.2 Morphology and fluid dynamics of cerebral aneurysms . 6 1.2.1 The role of hemodynamics . 10 1.3 Modeling the cerebral circulation . 12 1.3.1 The circle of Willis . 13 1.3.2 Cerebral aneurysms . 14 2 One-dimensional models for blood flow problems 15 2.1 Wave propagation phenomena in the cardiovascular system . 15 2.1.1 Modeling the vascular wall . 16 2.2 Formulation of the model . 17 2.2.1 A viscoelastic structural model for the vessel wall . 19 2.2.2 The linearized model . 21 2.3 Networks of 1D models . 27 2.4 Numerical discretization . 28 2.4.1 Numerical solution of the viscoelastic wall model . 29 2.5 Results and discussion . 30 2.5.1 Validation of the numerical model versus an analytical solution . 30 2.5.2 Wave propagation in a single 1-D vessel: a Gaussian pulse wave 32 2.5.3 Wave propagation in a single 1-D vessel: a sinusoidal wave . 34 2.5.4 A 1D model network: the circle of Willis . 35 3 Three-dimensional models for blood flow problems 39 3.1 Blood flow features in arteries . -
Name: Ejim Jessica Adanna Matric Number: 19/Mhs01/444 (De) College: Medicine and Health Sciences Department: Medicine and Surgery Course: Physiology Questions: 1
NAME: EJIM JESSICA ADANNA MATRIC NUMBER: 19/MHS01/444 (DE) COLLEGE: MEDICINE AND HEALTH SCIENCES DEPARTMENT: MEDICINE AND SURGERY COURSE: PHYSIOLOGY QUESTIONS: 1. Discuss the long term regulation of mean arterial blood pressure? 2. Write short notes on the following a. Pulmonary circulation b. Circle of Willis c. Splanchnic circulation d. Coronary circulation e. Cutaneous circulation 3. Discuss the cardiovascular adjustment that occurs during exercise. LONG TERM REGULATIONS OF MEAN ARTERIAL BLOOD PRESSURE. Firstly, mean arterial blood pressure is the average pressure existing in the arteries. It is not the arithmetic mean of the systole and diastolic pressure. To determine the mean pressure, diastolic pressure is considered than the systolic pressure because diastolic period of cardiac cycle is longer than the systolic period. Normal mean arterial pressure is 93mmHg LONG TERM REGULATIONS OF MEAN ARTERIAL BLOOD PRESSURE. it is also knowns as renal mechanism. Kidney plays an important role in the long term regulation of arterial blood pressure. When the blood pressure alters slowly in several days/ months/ years, the nervous mechanism adapts to the altered pressure and loses the sensitivity for changes. It cannot regulate the pressure anymore in such conditions, the renal mechanism operates efficiently to regulate the blood pressure. It is called long term regulation. The kidney regulates the arterial blood pressure in two ways A. By regulation of the extracellular fluid(ECF) volume. B. Through the renin-angiotensin mechanism. PULMONARY CIRCULATION It is otherwise called lesser circulation. Blood is pumped from the right ventricle to the lungs through pulmonary artery. Exchange of gases occurs between the blood and alveoli of the lungs at the pulmonary capillaries. -

Anatomical Atlas of the Upper Part of the Human Head for Electroencephalography and Bioimpedance Applications
Anatomical atlas of the upper part of the human head for electroencephalography and bioimpedance applications Fernando S Moura1,2,* and Roberto G Beraldo1 Leonardo A Ferreira1 Samuli Siltanen2 1Engineering, modelling and Applied Social Sciences Center, Federal University of ABC, São Bernardo do Campo, São Paulo, Brazil 2Department of Mathematics and Statistics, University of Helsinki, Helsinki, Finland *Corresponding author. Email: [email protected] Abstract Volume conductor problems in cerebral electrophysiology and bioimpedance do not have analytical solutions for nontrivial geometries and require a 3D model of the head and its electrical properties for solving the associated PDEs numer- ically. Ideally, the model should be made with patient-specific information. In clinical practice, this is not always the case and an average head model is of- ten used. Also, the electrical properties of the tissues might not be completely known due to natural variability. The objective of this work is to develop a 4D (3D+T) statistical anatomical atlas of the electrical properties of the upper part of the human head for cerebral electrophysiology and bioimpedance applications. The atlas is an important tool for in silico studies on cerebral circulation and electrophysiology that require statistically consistent data, e.g., machine learning, sensitivity analyses, and as a benchmark to test inverse problem solvers. The atlas was constructed based on MRI images of human individuals and comprises the electrical properties of the main internal structures and can be adjusted for specific electrical frequencies. The proposed atlas also comprises a time-varying model of arXiv:2108.08587v1 [physics.med-ph] 19 Aug 2021 arterial brain circulation, based on the solution of the Navier-Stokes equation in the main arteries and their vascular territories.