DOCSLIB.ORG

The Stirling Engine: the Heat Engine

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Stirling Engine: the Heat Engine Memorial University of Newfoundland Department of Physics and Physical Oceanography Physics 2053 Laboratory The Stirling Engine: The Heat Engine Under no circumstances should you attempt to operate the engine without supervision: it may be damaged if mishandled. Introduction Heat engines are generally described in terms of cyclic processes in which a gas absorbs heat QA at a high temperature, releases heat QB at a lower temperature, and performs an amount of work W . The efficiency of a heat engine is given by W η = ; QA however, even for an ideal (reversible) cycle in which there is no friction, efficiency is limited by the second law of thermodynamics. Q A p a T A Q A b T W A d Q TB B Q c B TB v Figure 1: The Carnot Cycle for an engine operating between two infinite heat baths. Carnot, in the 1820s, showed that the maximum theoretical efficiency available from a reversible heat engine depends only on the temperature change in the cycle. The Carnot 1 cycle is the reversible cycle which operates between two constant temperature baths. The pressure-volume diagram for the cycle is shown in Fig (1). Heat is absorbed and released as the gas is expanded or compressed along the isotherms a ! b and c ! d. During steps b ! c and d ! a, the gas is thermally isolated and changes temperature as it is expanded or compressed. The efficiency for this cycle is T η ≤ 1 − B TA where the equal sign applies only for a reversible (frictionless) cycle. The Carnot cycle is difficult to realize in practice and produces a relatively small amount of work per cycle. The Stirling cycle uses more than two thermal reservoirs but has the same maximum efficiency as the Carnot cycle and, for a given pair of temperatures and change in volume, produces more work per cycle. Robert Stirling (1790-1878) took out a patent for his engine in 1816. Unlike steam engines, it had no high pressure boiler and was thus somewhat safer. Its mechanical complexity limited the practical size and it was only used for small applications (e.g., farming) and only until the 1920s when the more powerful internal combustion engines became more popular. The Stirling engine continues to attract attention, periodically, as a more fuel efficient and potentially cleaner engine for some applications. Currently, the primary application of Stirling cycles is in refrigeration. The Stirling Cycle The pV diagram for an ideal Stirling cycle is shown in Fig (2). In our setup, two pistons move in the cylinder, shown schematically in Fig (3); the top region of the cylinder is heated by an electric heater and the lower walls of the cylinder are cooled by flowing water. The volume of air is changed by the movement of the lower piston. The upper piston moves the air from the heated region of the cylinder to the cooled region of the cylinder through a central hole in the piston which is filled with copper wool and is called the regenerator. When the air passes from the heated region, through the regenerator, to the cooled region, it releases heat to the copper wool and is cooled. When the air passes in the other direction, it retrieves this heat and is warmed. This shuttling of heat in and out of the regenerator is labeled QR in Figs 2 and 3. The regenerator can be thought of as a third, finite, thermal reservoir. The theoretical efficiency of a Stirling cycle operating between TA and TB is the same as for the Carnot cycle. The cycle is as follows: 2 p a Q A Q R b T Q R A d T Q B B c v Figure 2: The Stirling Cycle operating between the same temperature and volume limits as above. This cycle requires more than two thermal reservoirs. • [a] The volume is a minimum and most of the gas is in the heated part of the cylinder. The gas is at temperature TA. • [a ! b] The gas absorbs heat from the heater and expands at constant temperature. • [b] The gas is at its maximum volume and still at temperature TA. • [b ! c] The upper piston moves up forcing the gas through the regenerator and ex- tracting heat QR to leave the gas at temperature TB. • [c] The gas is still at its maximum volume, at temperature TB, and in contact with the cooled region of the cylinder. • [c ! d] The gas is compressed at constant temperature TB and releases heat QB to the cooling water. • [d] The gas is at its minimum volume and still at temperature TB. • [d ! a] The upper piston moves down and forces the gas through the regenerator where it reabsorbs heat QR and warms to TA. 3 QA a a b b QR d a b c QR d c d c QB Figure 3: Diagram to show the relative positions of the pistons during operation of the Stirling engine. Using the Pasco Interface Box 1. Check that the Rotary Motion Sensor is plugged into channel 1 (yellow) and channel 2 (black), and also that the differential pressure sensor is plugged into channel A. 2. Start the DataStudio program and click on Create Experiment. Select Rotary motion sensor and Pressure Sensor (Differential). 3. Click on the Rotary motion sensor icon to open the Sensor Properties window. Under the General tab, set the sample rate to 200 Hz; under Measurement, select Angular Position, measured in degrees (since we cannot measure volume directly). Repeat for 4 the pressure sensor, with pressure in kPa. 4. To create a graph of pressure versus volume: • Double-click on Graph (on the Displays menu). • Select Pressure as the data source. A set of axes will appear with pressure on the vertical axis and time on the horizontal axis. Click on the axis label `Time' and select Angular Position from the drop-down list. • Click Start to begin collecting data. Turn the engine slowly by hand and describe the correspondance between the position of the pistons and the resulting trace. Operation of the Stirling Engine as a Heat Engine Obtain your raw data as quickly as you can to prevent overheating of the con- necting wires due to high currents. 1. Start with a coil current of about 8 A. The engine is unlikely to start at lower currents. When the engine speed has stabilized, click on \Start" to obtain a new trace. At the same time determine the rate of rotation of the flywheel using the counter, and calculate the electrical power which is supplied to the heater coil. 2. Repeat the above steps, increasing the current by about ∼1 A each time. Do not let the coil current exceed 13 A. Turn off the Engine by switching off the heater current. Analysis 1. Save your pressure-volume data for each run using File - Export. 2. Import your raw data into a spreadsheet. You need pairs of (x; y) values corresponding to one complete loop only, as in Fig 4. Note that the \Angular Position" axis represents the volume change that occurs inside the cylinder so that the distance between maximum and minimum values on the horizontal axis of the graph corresponds to a volume change of 150 cm3. 3. The work done by the engine is obtained from the area of each loop. The area of a polygon with n vertices can be found from the Gauss-Green formula, n X (yi + yi+1) (xi − xi+1) i=1 2 5 140 120 100 80 60 Series1 Pressure (kPa) 40 20 0 -20 0 20 40 60 80 100 120 -20 angular position Figure 4: Typical output for one complete cycle from Stirling Engine experiment The curve needs to be a single loop that doesn't intersect itself. The loop must be closed so that the last x value is x1, and the last y value is y1. If necessary, add a copy of the first point to the end of the data list. 4. Calculate the area of the loop and the work done by the gas per cycle. Calculate also the power output and, by comparing with the electrical power input, the efficiency of the engine. 5. Summarize your results by plotting a graph of efficiency versus applied current, and discuss how well your results demonstrate the predictions of the Second Law. How much work is done in overcoming friction and other imperfections in the Engine? Reference: C. G. Deacon, R. Goulding, C. Haridass and B. de Young, Demonstration Experiments with a Stirling Engine, Physics Education 29, 180{183 (1994) 6.
Load more

Recommended publications
  • Abstract 1. Introduction 2. Robert Stirling
    Stirling Stuff Dr John S. Reid, Department of Physics, Meston Building, University of Aberdeen, Aberdeen AB12 3UE, Scotland Abstract Robert Stirling’s patent for what was essentially a new type of engine to create work from heat was submitted in 1816. Its reception was underwhelming and although the idea was sporadically developed, it was eclipsed by the steam engine and, later, the internal combustion engine. Today, though, the environmentally favourable credentials of the Stirling engine principles are driving a resurgence of interest, with modern designs using modern materials. These themes are woven through a historically based narrative that introduces Robert Stirling and his background, a description of his patent and the principles behind his engine, and discusses the now popular model Stirling engines readily available. These topical models, or alternatives made ‘in house’, form a good platform for investigating some of the thermodynamics governing the performance of engines in general. ---------------------------------------------------------------------------------------------------------------- 1. Introduction 2016 marks the bicentenary of the submission of Robert Stirling’s patent that described heat exchangers and the technology of the Stirling engine. James Watt was still alive in 1816 and his steam engine was gaining a foothold in mines, in mills, in a few goods railways and even in pioneering ‘steamers’. Who needed another new engine from another Scot? The Stirling engine is a markedly different machine from either the earlier steam engine or the later internal combustion engine. For reasons to be explained, after a comparatively obscure two centuries the Stirling engine is attracting new interest, for it has environmentally friendly credentials for an engine. This tribute introduces the man, his patent, the engine and how it is realised in example models readily available on the internet.
    [Show full text]
  • Feasibility Study Into Stirling Engines Application in Ship's Energy Systems
    Transactions on the Built Environment vol 42, © 1999 WIT Press, www.witpress.com, ISSN 1743-3509 Feasibility study into Stirling engines application in ship's energy systems S. Zmudzki, Faculty of Maritime Technology, Technical University of Szczecin, 71- 065 Szczecin, al Piastow 41, Poland E-mail: szmudzkia@shiptech. tuniv.szczecin.pl Abstract The possibility of utilization of solar energy as well as exhaust gas energy from main and auxiliary marine diesel engines for driving Stirling engines has been analysed. The Stirling engines are used for driving current generators. The solar dish Stirling units of 100 kW total effective power may be installed on a board of different type of ships. The system utilizing the exhaust gas energy has been provided with three-way catalyst which may lead to the reduction of emissions below limits established by appropriate regulations. 1 Introduction The Stirling engine belongs to a group of piston engines with so called external supply of heat energy, flowing then through metal walls of engine heater into working gas circulating in the working space. The heat energy supply may be realized or by means of direct effect of the high temperature energy source or by an intermediate heating system i.e. heat pipe or pool-boiler receiver. Thus, the design provides for the possibility of application of different types of heat energy of sufficiently large power. In particular, the advantages of Stirling engines are set off when using the alternative energy sources, especially waste heat energy, the operating costs for which are relatively lower in comparison with capital costs. In case of ship s energy installations, the solar energy available at appropriate geographical latitudes for ships having very large open deck surface / i.e.
    [Show full text]
  • Novel Hot Air Engine and Its Mathematical Model – Experimental Measurements and Numerical Analysis
    POLLACK PERIODICA An International Journal for Engineering and Information Sciences DOI: 10.1556/606.2019.14.1.5 Vol. 14, No. 1, pp. 47–58 (2019) www.akademiai.com NOVEL HOT AIR ENGINE AND ITS MATHEMATICAL MODEL – EXPERIMENTAL MEASUREMENTS AND NUMERICAL ANALYSIS 1 Gyula KRAMER, 2 Gabor SZEPESI *, 3 Zoltán SIMÉNFALVI 1,2,3 Department of Chemical Machinery, Institute of Energy and Chemical Machinery University of Miskolc, Miskolc-Egyetemváros 3515, Hungary e-mail: [email protected], [email protected], [email protected] Received 11 December 2017; accepted 25 June 2018 Abstract: In the relevant literature there are many types of heat engines. One of those is the group of the so called hot air engines. This paper introduces their world, also introduces the new kind of machine that was developed and built at Department of Chemical Machinery, Institute of Energy and Chemical Machinery, University of Miskolc. Emphasizing the novelty of construction and the working principle are explained. Also the mathematical model of this new engine was prepared and compared to the real model of engine. Keywords: Hot, Air, Engine, Mathematical model 1. Introduction There are three types of volumetric heat engines: the internal combustion engines; steam engines; and hot air engines. The first one is well known, because it is on zenith nowadays. The steam machines are also well known, because their time has just passed, even the elder ones could see those in use. But the hot air engines are forgotten. Our aim is to consider that one. The history of hot air engines is 200 years old.
    [Show full text]
  • 25 Kw Low-Temperature Stirling Engine for Heat Recovery, Solar, and Biomass Applications
    25 kW Low-Temperature Stirling Engine for Heat Recovery, Solar, and Biomass Applications Lee SMITHa, Brian NUELa, Samuel P WEAVERa,*, Stefan BERKOWERa, Samuel C WEAVERb, Bill GROSSc aCool Energy, Inc, 5541 Central Avenue, Boulder CO 80301 bProton Power, Inc, 487 Sam Rayburn Parkway, Lenoir City TN 37771 cIdealab, 130 W. Union St, Pasadena CA 91103 *Corresponding author: [email protected] Keywords: Stirling engine, waste heat recovery, concentrating solar power, biomass power generation, low-temperature power generation, distributed generation ABSTRACT This paper covers the design, performance optimization, build, and test of a 25 kW Stirling engine that has demonstrated > 60% of the Carnot limit for thermal to electrical conversion efficiency at test conditions of 329 °C hot side temperature and 19 °C rejection temperature. These results were enabled by an engine design and construction that has minimal pressure drop in the gas flow path, thermal conduction losses that are limited by design, and which employs a novel rotary drive mechanism. Features of this engine design include high-surface- area heat exchangers, nitrogen as the working fluid, a single-acting alpha configuration, and a design target for operation between 150 °C and 400 °C. 1 1. INTRODUCTION Since 2006, Cool Energy, Inc. (CEI) has designed, fabricated, and tested five generations of low-temperature (150 °C to 400 °C) Stirling engines that drive internally integrated electric alternators. The fifth generation of engine built by Cool Energy is rated at 25 kW of electrical power output, and is trade-named the ThermoHeart® Engine. Sources of low-to-medium temperature thermal energy, such as internal combustion engine exhaust, industrial waste heat, flared gas, and small-scale solar heat, have relatively few methods available for conversion into more valuable electrical energy, and the thermal energy is usually wasted.
    [Show full text]
  • A Stirling Engine for Automotive Applications Steve Djetel, Sylvie Bégot, François Lanzetta, Eric Gavignet, Wissam S
    A Stirling Engine for Automotive Applications Steve Djetel, Sylvie Bégot, François Lanzetta, Eric Gavignet, Wissam S. Bou Nader To cite this version: Steve Djetel, Sylvie Bégot, François Lanzetta, Eric Gavignet, Wissam S. Bou Nader. A Stirling Engine for Automotive Applications. Vehicle Power and Propulsion Conference, Dec 2017, Belfort, France. hal-02131002 HAL Id: hal-02131002 https://hal.archives-ouvertes.fr/hal-02131002 Submitted on 16 May 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A Stirling engine for automotive applications Steve Djetel, Sylvie Bégot, François Lanzetta, Wissam S. Bou Nader Eric Gavignet Technical center of Vélizy FEMTO-ST Institute PSA Group Univ. Bourgogne Franche-Comté, CNRS 78943 Velizy, France Département ENERGIE [email protected] 90000 Belfort, France [email protected] Abstract — This paper describes a Stirling Engine used as an the fuel and air are combusted under pressure and expanded Auxiliary Power Unit in a Series Hybrid Vehicle. The engine directly to produce work [4-5]. The Stirling technology is modeling is presented, then its integration in the vehicle power interesting for two major raisons: (1) the theoretical train is described.
    [Show full text]
  • Comparison of ORC Turbine and Stirling Engine to Produce Electricity from Gasified Poultry Waste
    Sustainability 2014, 6, 5714-5729; doi:10.3390/su6095714 OPEN ACCESS sustainability ISSN 2071-1050 www.mdpi.com/journal/sustainability Article Comparison of ORC Turbine and Stirling Engine to Produce Electricity from Gasified Poultry Waste Franco Cotana 1,†, Antonio Messineo 2,†, Alessandro Petrozzi 1,†,*, Valentina Coccia 1, Gianluca Cavalaglio 1 and Andrea Aquino 1 1 CRB, Centro di Ricerca sulle Biomasse, Via Duranti sn, 06125 Perugia, Italy; E-Mails: [email protected] (F.C.); [email protected] (V.C.); [email protected] (G.C.); [email protected] (A.A.) 2 Università degli Studi di Enna “Kore” Cittadella Universitaria, 94100 Enna, Italy; E-Mail: [email protected] † These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +39-075-585-3806; Fax: +39-075-515-3321. Received: 25 June 2014; in revised form: 5 August 2014 / Accepted: 12 August 2014 / Published: 28 August 2014 Abstract: The Biomass Research Centre, section of CIRIAF, has recently developed a biomass boiler (300 kW thermal powered), fed by the poultry manure collected in a nearby livestock. All the thermal requirements of the livestock will be covered by the heat produced by gas combustion in the gasifier boiler. Within the activities carried out by the research project ENERPOLL (Energy Valorization of Poultry Manure in a Thermal Power Plant), funded by the Italian Ministry of Agriculture and Forestry, this paper aims at studying an upgrade version of the existing thermal plant, investigating and analyzing the possible applications for electricity production recovering the exceeding thermal energy. A comparison of Organic Rankine Cycle turbines and Stirling engines, to produce electricity from gasified poultry waste, is proposed, evaluating technical and economic parameters, considering actual incentives on renewable produced electricity.
    [Show full text]
  • And High Temperature Differential Stirling Engines
    COMPARISON OF LOW- AND HIGH TEMPERATURE DIFFERENTIAL STIRLING ENGINES S. IWAMOTO*1, F. TODA*1, K. HIRATA*1 M. TAKEUCHI*2 and T. YAMAMOTO*3 *1Department of Mechanical Engineering, Faculty of Engineering, Saitama University, Japan *2Suction Gas Engine MFG. Co., Ltd., Japan *3National Institute for Research and Environment, Japan ABSTRACT Stirling engines can be operated with various heat sources. We have developed several Stirling engines, included a low temperature differential Stirling engine using hot spring heat and a high temperature differential Stirling engine using a combustion gas as the fuel. These engines have different features and characteristics, and have different thermal performance. In this paper, the performances of these difference types of Stirling engines were measured, were compared using the normalized values. INTRODUCTION In the field of the low temperature differential Stirling engines, several small Stirling engines have developed by I. Kolin, J. R. Senft and so on1),2). We have being developed the low temperature differential Stirling engine with several hundreds wattage of an output power3). The engine uses hot spring heat or hot water from industrial waste heat as the fuel. In this paper, we measured heat losses and powers of the engine in order to estimate the engine performance. Then the performance of a prototype of the low temperature differential Stirling engine (LDSE) was compared with that of a high temperature differential Stirling engine (HDSE) after their experimental results had been normalized. Figure 1 Feature of LDSE STRUCTURE OF LDSE Figure 1 and Fig. 2 show the features and structure of LDSE. Table 1 shows specifications of this engine and HDSE5) used to compare the performances.
    [Show full text]
  • Pursuit of Power NASA’S Propulsion Systems Laboratory No
    Pursuit of Power NASA’s Propulsion Systems Laboratory No. 1 and 2 By Robert S. Arrighi National Aeronautics and Space Administration NASA History Program Office Public Outreach Division NASA Headquarters Washington, DC 20546 SP–2012–4548 2012 Library of Congress Cataloging-in-Publication Data Arrighi, Robert S., 1969- Pursuit of Power : NASA’s Propulsion Systems Laboratory, No. 1 & 2 / Robert S. Arrighi. p. cm. -- (NASA history series) (NASA SP ; 2012-4548) Includes bibliographical references and index. 1. Propulsion Systems Laboratory (U.S.)--History. 2. Wind tunnels. 3. Hypersonic wind tunnels. 4. Aerodynamics--Research--United States--History--20th century. 5. Propulsion systems--United States--History--20th century. 6. NASA Glenn Research Center. I. United States. NASA History Division. II. Title. III. Title: NASA’s Propulsion Systems Laboratory, No. 1 & 2. IV. Title: Propulsion Systems Laboratory, No. 1 & 2. TL568.P75A77 2012 629.1’1072--dc23 2011032380 • Table of Contents • Introduction ................................................................................................................................................ vii Condensed History of the PSL ......................................................................................................... ix Preserving the PSL Legacy ................................................................................................................. ix Endnotes for Introduction .................................................................................................................
    [Show full text]
  • The Gamma Stirling Engine
    The Gamma Stirling Engine Leon van Dommelen July 25, 2019 Consider the Stirling cycle as shown in figure 1. Read the legend of the figure to identify the key components. The crucial stage for getting power out is (b). Here the power piston is pushing against the flywheel, increasing its speed. This part of the cycle is called the power stroke; it makes the engine produce its power. Note that most of the air in the displacer cylinder is red hot. That makes it want to expand, raising the pressure way up. (Since the air can easily move around the displacer piston, the cold air is at the same high pressure as the hot one. OK, if you insist, there is some resistance in flowing around the displacer through the regenerator stuff. But that should be small. Sometimes students mistakingly think that the hot air is at high pressure and the cold air at low. But that is not possible because there is no physical barrier between the two to support such a pressure difference. At any given stage in the cycle, it is only the density and not the pressure that is different for the hot and cold air.) The high pressure pushes forcefully against the power piston, and so on the attached flywheel, increasing the flywheel’s velocity and kinetic energy. So the device is producing power. The bad news is the later stage (d). Here the piston is going the other way. Now the flywheel must compress the air again, which slows it down. This stage is called the compression stroke.
    [Show full text]
  • Stirling Engine)
    Heat Cycles Hot air engine (Stirling engine) OPERATE A FUNCTIONAL MODEL OF A STIRLING ENGINE AS A HEAT ENGINE Operate the hot-air engine as a heat engine Demonstrate how thermal energy is converted into mechanical energy Measure the no-load speed as a function of the thermal power UE2060100 04/16 JS BASIC PRINCIPLES The thermodynamic cycle of the Stirling engine While the working piston is in its top dead centre posi- (invented by Rev. R. Stirling in 1816) can be pre- tion: the displacement piston retracts and air is dis- sented in a simplified manner as the processes placed towards the top end of the large cylinder so that thermal input, expansion, thermal output and com- it cools. pression. These processes have been illustrated by The cooled air is compressed by the working piston schematic diagrams (Fig. 1 to Fig. 4) for the func- extending. The mechanical work required for this is tional model used in the experiment. provided by the flywheel rod. A displacement piston P1 moves upwards and displac- If the Stirling engine is operated without any mechanical es the air downwards into the heated area of the large load, it operates with at a speed which is limited only by cylinder, thereby facilitating the input of air. During this internal friction and which depends on the input heating operation the working piston is at its bottom dead centre energy. The speed is reduced as soon as a load takes position since the displacement piston is ahead of the up some of the mechanical energy. This is most easily working piston by 90°.
    [Show full text]
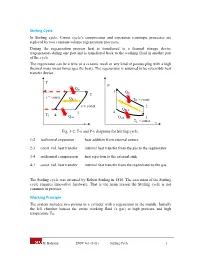
  • Stirling Cycle Working Principle
    Stirling Cycle In Stirling cycle, Carnot cycle’s compression and expansion isentropic processes are replaced by two constant-volume regeneration processes. During the regeneration process heat is transferred to a thermal storage device (regenerator) during one part and is transferred back to the working fluid in another part of the cycle. The regenerator can be a wire or a ceramic mesh or any kind of porous plug with a high thermal mass (mass times specific heat). The regenerator is assumed to be reversible heat transfer device. T P Qin TH 1 1 Q 2 in v = const. Q Reg. TH = const. v = const. 2 QReg. 3 4 TL 4 Qout Qout 3 T = const. s L v Fig. 3-2: T-s and P-v diagrams for Stirling cycle. 1-2 isothermal expansion heat addition from external source 2-3 const. vol. heat transfer internal heat transfer from the gas to the regenerator 3-4 isothermal compression heat rejection to the external sink 4-1 const. vol. heat transfer internal heat transfer from the regenerator to the gas The Stirling cycle was invented by Robert Stirling in 1816. The execution of the Stirling cycle requires innovative hardware. That is the main reason the Stirling cycle is not common in practice. Working Principle The system includes two pistons in a cylinder with a regenerator in the middle. Initially the left chamber houses the entire working fluid (a gas) at high pressure and high temperature TH. M. Bahrami ENSC 461 (S 11) Stirling Cycle 1 TH TL QH State 1 Regenerator Fig 3-3a: 1-2, isothermal heat transfer to the gas at TH from external source.
    [Show full text]
  • Design of a 2.5Kw Low Temperature Stirling Engine for Distributed Solar Thermal Generation
    Design of a 2.5kW Low Temperature Stirling Engine for Distributed Solar Thermal Generation Mike He∗ and Seth Sandersy University of California - Berkeley, Berkeley, CA, 94720, USA This paper focuses on the design of a Stirling engine for distributed solar thermal ap- plications. In particular, we design for the low temperature differential that is attainable with distributed solar collectors and the low cost that is required to be competitive in this space. We will describe how these considerations drive the core design, the methodology for improving the design, and summarize progress made in fabrication of the engine for experimentation. Stirling engines can have broad significance and technological advantages for distributed renewable energy applications. A key advantage of a solar thermal system is that they can incorporate thermal energy storage in a cost-effective manner. In addition, Stirling engine systems are fuel-flexible with respect to the source of thermal energy and unprocessed waste heat can be harvested for CHP purposes as well. The ability to extract unconverted thermal energy for waste heat applications greatly improves the overall thermal efficiency of the system. I. Introduction enewable energy technology will need to address important challenges in order to be adopted at high Rpenetrations in a modern electric grid. These include achieving low enough cost to be economically attrac- tive and mitigating the variability inherent in renewable energy sources, a problem most directly addressed by energy storage. We propose a Stirling-engine-based solar thermal system for distributed generation of electricity as a renewable energy technology that addresses these challenges. The proposed system, as shown in Figure1, is comprised of a passive solar collector, a hot thermal storage subsystem, a Stirling engine for energy conversion, and a waste heat recovery system to implement combined heat and power.
    [Show full text]