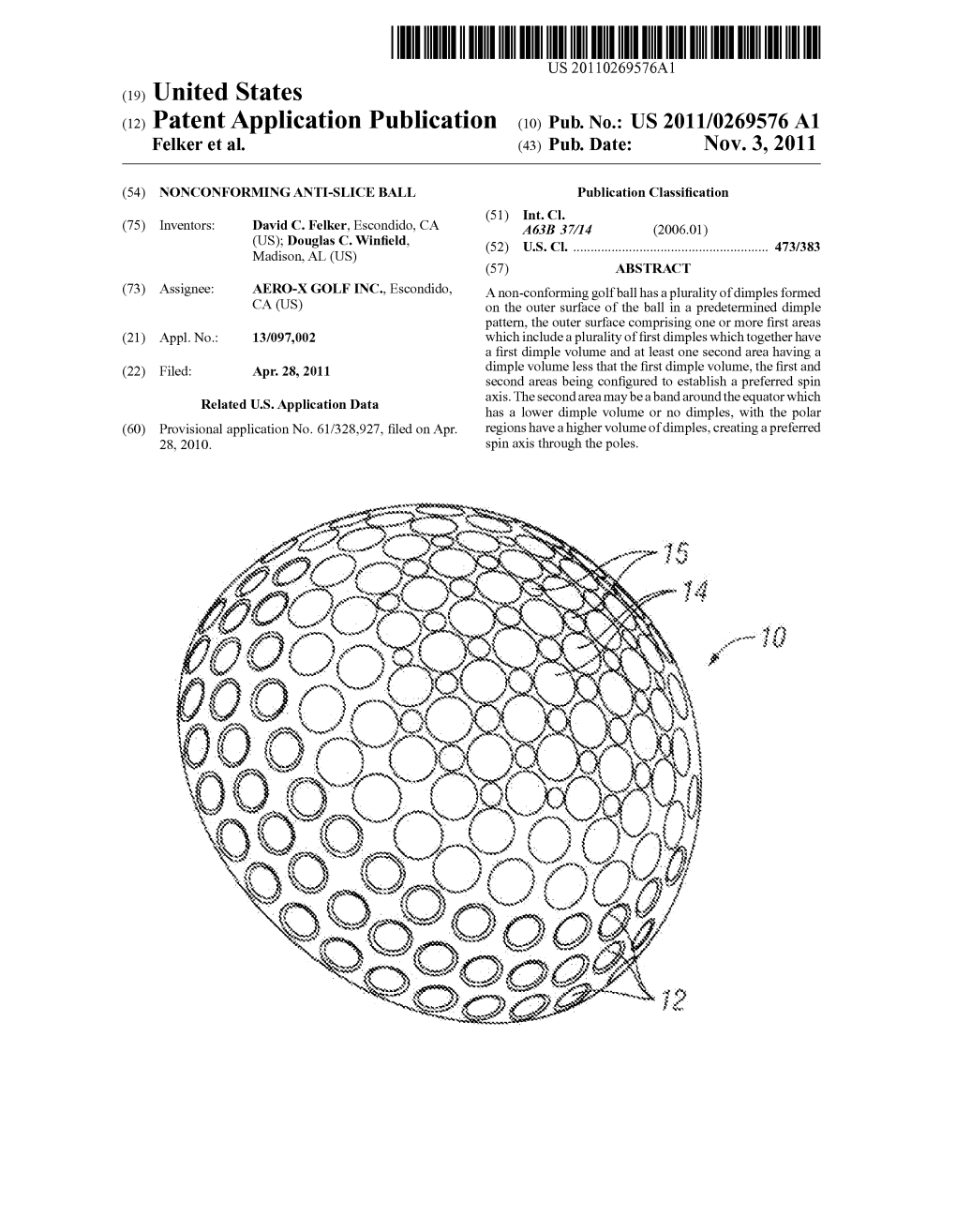
US 2011/0269.576A1 Felker Et Al
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

FRONT NINE NEWS Page 1 Volume 15, Issue 1 March 2011
FRONT NINE NEWS Page 1 Volume 15, Issue 1 March 2011 A quarterly publication of the Northwestern Pennsylvania Golf Course Superintendents Association, Inc. NWPGCSA 2011 Committees March Business Meeting Meetings/Education Thursday, March 17, 2011 Wayne Rodgers/Mike Bochert (Yes, this is St. Patrick’s Day) Membership MEETING AGENDA Jerry Rice 4:00-5:00 PM Social Hour Welfare Dave Stull/Julie Powell 5:00 PM Buffet Dinner (w/St. Patrick’s Day fare) Employment 6:00 PM Business Meeting Jerry Rice Meeting Fee - $35 Finance Place: Rob Goring Venango Valley Inn & Golf Course Dress Code: Casual Attire Route 19 GCSAA/PGCSA Venango, PA 16440 Bar on site. Dave Stull/Joe Giardina Directions: Open guest policy for all Scholarship/Research From the South: From I-79, take members Durbin Loreno the Saegertown Exit heading East on Rt. 198 towards Saegertown. Credit cards accepted by Venango Valley Nominations/Ethics Go approximately 3 miles to a “T” intersection. Turn left on Rt. 19 Host Superintendent, Dave Stull heading towards Venango. Durbin Loreno Venango Valley Inn is another 3 miles on the left. RSVP to Julie by March 14th GCSAA LIAISONS From the North: Take Rt. 19 at (724) 421-7588 through the town of Venango. NOTE: While reservations are Certification Attester Venango Valley Inn is just outside needed for food preparation, last Joe Giardina of town on the right. minute reservations are understood due to the nature of the turf industry. We have Education Programming Inside This Issue never turned anyone away. Mike Bochert Chapter News: Presidents Message Page 3 Snow Mold Survey Page 6 IF THERE IS A CHECK IN First Tee Program THIS BOX, WE HAVE NOT Durbin Loreno PA News: RECEIVED YOUR 2011 DUES. -

An Exclusive with Lee Westwood
DECEMBER 2014 32 ISSUE 171 SPECIAL FEATURES 24 18 Glitz, Glamour And Game! When golf meets entertainment, you would expect Mission Hills Group to do it biggest and best – and this is exactly what the pioneering leisure and life- style conglomerate delivered with the Mission Hills World Celebrity Pro-Am. 66 Black Hat Tips-Tony Meechai: Black Hat Golf Tips Lawyers have to pass the “bar” examination. Now, here’s the ‘bar’ exams I 24 APGS 2014 Registers High Marks! want you to pass and understand! 10 The 2014 Asia Pacific Golf Summit ended in Singapore on a high note with members of the golf industry giving the event the thumbs up for setting The Great White Shark aka Greg Norman was scathing with the tone and providing a positive outlook for the future of golf in Asia. his response when asked for his opinion on the need to 32 The “Big Easy” Aces It In Malaysia renovate golf courses that have fallen into neglect. “I have There’s no denying the fact that Ernie Els aka the “Big Easy” is ecstatic over one word for this – sustainable. Shame on a lot of developers the golf course he designed on the Malaysian island of Langkawi. It Is COVER STORY and golf course designers in the 80’s and 90’s who built golf earning the golfer/designer top honours on a global scale. courses with unlimited budgets,” was his sharp reply. 36 Rose And Poulter – The Perfect Match Justin Rose and Ian Poulter want golfers to enjoy themselves when play- EQUIPMENT FOCUS ing on their new course at Mission Hills Dongguan in China – and the two Ryder Cup stars did just that when they christened the layout with a 50 Singapore – A Force In Golf? adidas and with his move, the bold initiative to towering flight path and carry those hazards that one-off Match Play challenge. -

My Golf Buddy's 12 Gifts of Christmas for the Golfer Who Has Everything
My Golf Buddy’s 12 Gifts of Christmas for the Golfer Who Has Everything Are you searching for that perfect Christmas gift for the golfing boss or special loved one? MyGolfBuddy.com’s 12 Gifts of Christmas for the Golfer Who Has Everything has hand selected 12 gifts you can put under the tree that any golfer would love to open this Christmas season. You will look like a Christmas present genius when any one of these obscure golf gifts is unveiled. Like Santa, check this list twice. It’s a compilation of cool technologies and the hottest products in golf today ensuring your Christmas Gift will not be forgotten. This Christmas list doesn’t include your typical golf shirt or shoes. All 12 gifts are unique in the golf world and even the most avid golfer probably doesn’t have one item on this list. For example, cure the golfer in your life’s dreaded “Death Grip” with the LeviTee Glove. The LeviTee glove, with Finger Separation Technology (FST), has pads between the fingers that help reduce tension resulting in better contact which can increase distance. Have you heard enough stories about the critical putt that didn’t go in? The Point N Putt Putter is what you want under the tree. This putter, with alignment technology, is proven to significantly improve alignment by independent tests conducted by Sam PuttLab. Additional gifts on the MyGolfBuddy list include the Krank Driver, the authority in distance drivers, the SwingBox, home driving range, and Polara Golf’s illegal golf balls that fly up to 75% straighter than any ball on the market. -

Celebrating R.T
Sponsored by: May 27, 2011 Vol. 11, N o. 21 Buck’s Run Golf Club • http://bucksrun.com/golf/proto/bucksrun/ • Tour the Course Video with Jerry Matthews http://youtube.com/watch?v=qxuMfR0vN3o n o i t a d n u o F f l Arcadia Bluffs o G • Website: http://arcadiabluffs.com n a g i • Golf & Lodging Rates: http://tiny.cc/9vx3f h c i M • Tour the Course: http://tiny.cc/13yy1 f o y s e t r u o c o t o h P Arthur Hills, Michigan Golf Hall of Fame, Class of 2011 LochenHeath Golf Course • Website: http://lochenheath.com • Video: http://tiny.cc/k4txr In This Issue: __/ Run for the Roses II: By Bill Shelton __/ Finding a Game for the Rest of Us __/ Michigan Golfer Television: Michigan Golf Hall of Fame __/ Alternative Ways to Play Golf: By Chris Miles of Miles of Golf __/ Play Golf America to be Held at Fox Hills __/ Michigan Golfer Magazine Online - Spring Issue Sandy Ridge Golf Course • Website: http://golfsandyridge.com __/ Tee It Forward: PGA and USGA Thoughts • Video: http://tiny.cc/y18s8 __/ Up North Resorts Upbeat on Michigan Economy: By Tom Walsh of the Detroit Free Press __/ More Game Changing Ideas: By Scott Seifferlein __/ Michigan Has First Regional NCAA Title - Lion Kim Had a Career Best Round __/ Minzey's Musings __/ Michigan Golfer Television Channel - 2011 Shows __/ Michigan Golf Calendar __/ Michigan Golfer Archives Treetops Resort - Celebrating R.T. Jones http://michigangolfer.com/mgn/archives.html Masterpiece 25th Anniversary __/ Michigan Golf History http://michigangolfer.com/mgn/history.html • Website: http://treetops.com __/ Michigan -
![[Pdf] How to Increase Your Golf Swing Speed](https://docslib.b-cdn.net/cover/9059/pdf-how-to-increase-your-golf-swing-speed-4119059.webp)
[Pdf] How to Increase Your Golf Swing Speed
Additional information >>> HERE <<< How to download how to increase your golf swing speed user review- how to access icloud photo sharing Download from original url --> http://dbvir.com/jaacob/pdx/1199t1066/ Tags: kxhu39 best way to get cheapest how to increase your golf swing speed details- golf swing dvd download, how to start a blog roll - user experience, golf swing impact position drills : how to getting swing man golf, how do i swing man golf real user experience, lowprice swing man golf-- how to start a business with 30000, fresh information golf swing arms body connected - - a closer look, how to download how to increase your golf swing speed user review- how to access icloud photo sharing. cheap golf course membership melbourne buy nike golf clubs cheap lowest price on golf shoes golf clubs sale adelaide golf clubs sale used cost to build a mini golf course cost of bringing golf clubs on a flight j lindeberg golf shoes review golf tips casting swing ecco golf shoes best price best performing golf ball 2013 best golf shoes for wide feet review golf shoes 2011 golf clubs lowest prices arizona golf course aeration schedule golf pro openings why are there three golf balls on the moon krank golf drivers ebay pinterest golf ball ants golf course yardage maps public golf courses near eden prairie mn golf pro jobs texas hk professional golf association golf drivers cheap uk shop titleist golf balls polara golf ball xds review review noodle plus golf ball cost of building a golf course how much does it cost to operate a golf course cheap -

November-December 2011
The Art of Service Borman Wins DSA Plus No-Till Fairways Fisher Draws Line [ search engine powered by magazooms.com ] Want a mower that performs as well in the shop as on the green? With our new SL PrecisionCut™ Walk Greens Mowers, you can set height-of-cut with a cordless drill, switch rollers by simply removing two bolts, and add an easy-to-adjust front push brush, Greens Tender Conditioner or rotary brush. 3OXVJHWWKHƠDZOHVVƟQLVKRQ\RXUJUHHQVWKDWRXUZDONHUVDUH known for. Interested? Contact us to learn more or visit JohnDeere. com/Golf. Think Ahead. 46524 SHOWTURF REVELS TURF AND TRACTOR, LLC GREENVILLE TURF & TRACTOR Hilton Head, SC Fuquay-Varina, NC Piedmont, SC Savannah, GA Myrtle Beach, SC Murfreesboro, TN Boynton Beach and Naples, FL 800-849-5469 Hernando, MS 888-746-8873 866-485-8873 BR1OCU1CG46524 -GTT8X111101CG-4C-00359114 [ search engine powered by magazooms.com ] President JOHN F. DAVIS Secession Golf Club Beaufort, SC (843) 522-4642 [email protected] Vice-President November -December 2011 DOUGLAS C. LOWE, CGCS Greensboro Country Club Greensboro, NC Columns and Departments (336) 691-5822 [email protected] 2 President’s Message Secretary-Treasurer 4 Executive Director’s Message STEPHEN T. HAMILTON, CGCS Dunes Golf and Beach Club 6 The Pat Jones Index Myrtle Beach, SC 10 On the Road (843) 449-7332 [email protected] 12 Turf Talk Past President 14 USGA Green Section JEFFREY S. CONNELL 16 SC Government Relations Fort Jackson Golf Course Fort Jackson, SC 17 NC Government Relations (803) 787-4723 [email protected] 18 Headliners 34 Local Association News Directors JEREMY D. -

Multi Tenant Office Investment Opportunity
INVESTMENT OPPORTUNITY 2385 CAMINO VIDA ROBLE CARLSBAD, CA 92011 MULTI TENANT OFFICE INVESTMENT OPPORTUNITY OFFERED AT: $5,671,000 | 5.75% CAP EXECUTIVE SUMMARY PROPERTY INFORMATION AREA OVERVIEW TABLE OF CONTENTS EXECUTIVE SUMMARY 4 Offering Summary 5 Investment Highlights 6 Rent Roll 7 Cash Flow Projection 8 Replacement Cost Summary PROPERTY INFORMATION 10 Location Maps 11 Site Description 12 Floor Plans 14 Carlsbad Market Overview 20 Value Add Component 21 Property Photos 23 Aerials AREA OVERVIEW 29 Carlsbad Overview 30 San Diego County Overview 31 Demographics Confidentiality Agreement & Disclosures CAPITAL MARKETS CONTACTS RYAN BARR RYAN BENNETT Principal Principal 760.448.2446 760.448.2449 [email protected] [email protected] CA Lic#01338994 CA Lic#01826517 LOCAL MARKET EXPERTS JEFF ABRAMSON GREG GERSHMAN Principal Principal 760.929.7835 760.929.7861 [email protected] [email protected] CA Lic#00956805 CA Lic#01909272 Color Scheme RGB R:145 / G:0 / B:40 CMYK C:0 / M:100 / Y:65 / K:47 RGB R:119 / G:120 / B:123 CMYK C:0 / M:0 / Y:0 / K65 Fonts GOTHAM/ BLACK GOTHAM/ MEDIUM GOTHAM/ LIGHT 23852385 CAMINO CAMINO VIDA VIDA ROBLE ROBLE | | Carlsbad, Carlsbad, CA CA | | 2 2 2385 EXECUTIVE SUMMARY CAMINO VIDA ROBLE CARLSBAD, CA 92011 EXECUTIVE SUMMARY PROPERTY INFORMATION AREA OVERVIEW Offering Summary Investment Highlights Rent Roll Cash Flow Projection Replacement Cost Summary -- OFFERING SUMMARY -- INVESTMENT HIGHLIGHTS TENANT OVERVIEW Offering Price: $5,671,000 Securitas Security Svc 1,500 SF Net Operating Income: $326,073 Remington L&W Holdings 1,024 SF Grant IP 1,546 SF Cap Rate - Year 1: 5.75% Mike Thomas 2,000 SF Price/SF: $201 John Roach 1,531 SF Learning Genie 1,045 SF PROPERTY OVERVIEW Ramesh Enterprises 1,515 SF Property Type: Multi-Tenant (16 Units) Summit Capital 1,194 SF 2385 Camino Vida Roble EA Outsource & Bus. -

Antitrust Analysis of Sports Leagues
Munich Personal RePEc Archive Antitrust Analysis of Sports Leagues Pelnar, Gregory Lexecon 12 October 2007 Online at https://mpra.ub.uni-muenchen.de/5382/ MPRA Paper No. 5382, posted 20 Oct 2007 UTC Antitrust Analysis of Sports Leagues Gregory J. Pelnar Lexecon 332 S. Michigan Ave. Suite 1300 Chicago, IL 60604 (312) 322-0238 [email protected] Draft: October 12, 2007 Table of Contents Introduction 7 Chapter 1: What Is a Sports League? 9 A Brief History of the Major Sports Leagues in the United States 9 National Football League 10 Major League Baseball 12 National Basketball Association 13 National Hockey League 14 National Collegiate Athletic Association 16 Major League Soccer 18 Women’s National Basketball Association 19 Key Differences Between Sports Leagues 20 Sanctioning Bodies as a Form of Sports League 22 Economic Theories of Sports Leagues 23 Sports leagues as natural monopolies 23 Sports leagues as joint ventures 25 Sports leagues as cartels 27 Chapter 2: Basics of Antitrust Analysis 29 The Antitrust Laws 29 Exceptions to the Antitrust Laws 30 Judicial ‘interstate commerce’ exemption 30 Judicial ‘single-entity’ exemption 34 Statutory exemptions 37 Non-statutory exemptions 39 Proving Antitrust Violations 41 Proving violations of section 1 of the Sherman Act 41 Proving violations of section 2 of the Sherman Act 43 Proving violations of section 7 of the Clayton Act 49 - - 2 Chapter 3: Sports Leagues vs. Their Own Member Teams 51 Basics of Cartels 51 Basics of Joint Ventures 53 Externalities 56 Organizational problems 56 Joint venture instability 57 Team Antitrust Challenges to Sports League Rules and Policies 57 Public ownership restrictions 58 Sponsorship and licensing arrangements 61 Dallas Cowboys 61 New York Yankees 64 Television restrictions 67 NCAA 68 Chicago Bulls 72 Team relocation 75 San Francisco Seals 76 Oakland Raiders 77 San Diego Clippers 80 New England Patriots 81 Chapter 4: Sports Leagues vs. -

Attendees As of May 2, 2013
ATTENDEES AS OF MAY 2, 2013 DESCRIPTIONS PROVIDED BY ATTENDEES Stan Abrams, Senior Tour Players marketing. AJ Ali, Founder, Golf To End Cancer (Monday panelist) Ali is a wellness-focused writer & TV host, and the Founder of Golf To End Cancer, a nonprofit initiative promoting wellness and cancer prevention throughout the U.S. He is co-author of "The True Champion's 30-Day Challenge," a book helping people take their life to another level in mind, body and spirit. Steve Anderson, PGA Professional; Steve & Mitch Show - Creator and co-host of the weekly web show, ‘The Steve and Mitch Golf Show’ featuring actor and celebrity golfer Mitch Laurance. The Steve and Mitch Show features instruction, humor and golf stories. Author of 3 best-selling books on golf. ‘On the Other Hand’ is the only book for left-handed golfers and is now in its 5th printing. Only left-handed PGA Master Professional. Creator of ‘The Mirror Image Golf Swing. Steve Aronson, 240GOLF (See EXHIBITING COMPANIES list) John Ashton, Host and owner, Those Weekend Golf Guys radio program airing twice each weekend with 4 hours of original programming. We focus on the average golfer and how he/she can have more fun with the game, with new places to play, equipment choices, learning techniques or just interesting conversation with personalities in and around the golf business. Our show is heard in markets in and around Louisville and Southern Indiana ,with more outlets being added soon. The show can be heard via the Internet through our website, http://thoseweekendgolfguys.com Steve Asman, CEO, Gustbuster/Sunbuster Rick Auerbach, Partner, GolfCoachDirect.com (See EXHIBITING COMPANIES list) George Baker, Razor Golf (See EXHIBITING COMPANIES list) Ian Barrett, Global Marketing, Cobra Puma Golf (See EXHIBITING COMPANIES list) John Barrett-Publisher, FORE Georgia, the Official Publication of the GAPGA- Published monthly (Feb.- Nov.) FORE Georgia goes out monthly to 70,000+ core golfers throughout the State. -

An Insight Into the Acceptable Use & Assessment of Lower-Limb Running
An Insight into the Acceptable Use & Assessment of Lower-limb Running Prostheses in Disability Sport BRYCE T.J. DYER A thesis submitted in partial fulfilment of the requirements of Bournemouth University for the degree of Doctor of Philosophy July 2013 Bournemouth University COPYRIGHT STATEMENT This copy of the thesis has been supplied on condition that anyone who consults it is understood to recognise that its copyright rests with its author. No quotation from the thesis and no information derived from it may be published without the author’s prior consent. 1 DEDICATION This thesis is dedicated to the memory of Jeff Dyer (1949-2012). A great father, whose mental and physical endurance were without equal. 2 ACKNOWLEDGEMENTS I would like to thank Professor Siamak Noroozi, Dr Philip Sewell & Dr Sabi Redwood for their time, support and guidance which helped make this research project so enjoyable. Furthermore, I would like to thank both Shelley Broomfield and Andy Callaway for their assistance with some of the data collection. This journey would not have been possible without any of them. Several friends and colleagues were also extremely helpful in either offering advice, encouragement or providing insight with respect to the PhD experience. They include: Dr Bob Eves, Dr Mehran Koohgilani, Dr Mihai Dupac, Professor Peter Hogarth and Professor John Vinney. Finally, special thanks go to my partner Michaela who supported my experience and all of the occasional frustrations that sometimes came with it. 3 ABSTRACT Sports technology can be any product or system used to facilitate, train or influence an athlete’s performance. -

WO 2013/052925 A2 11 April 2013 (11.04.2013) P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization I International Bureau (10) International Publication Number (43) International Publication Date WO 2013/052925 A2 11 April 2013 (11.04.2013) P O P C T (51) International Patent Classification: (81) Designated States (unless otherwise indicated, for every A63B 37/14 (2006.01) A63B 53/02 (2006.01) kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, (21) International Application Number: BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, PCT/US20 12/059 140 DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, (22) International Filing Date: HN, HR, HU, ID, IL, IN, IS, JP, KE, KG, KM, KN, KP, 5 October 2012 (05. 10.2012) KR, KZ, LA, LC, LK, LR, LS, LT, LU, LY, MA, MD, ME, MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, (25) Filing Language: English NO, NZ, OM, PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, (26) Publication Language: English RW, SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, (30) Priority Data: ZM, ZW. 61/543,764 5 October 201 1 (05. 10.201 1) US (84) Designated States (unless otherwise indicated, for every (71) Applicant (for all designated States except US): AERO-X kind of regional protection available): ARIPO (BW, GH, GOLF, INC. [US/US]; 2380 Camino Vida Roble, #E, GM, KE, LR, LS, MW, MZ, NA, RW, SD, SL, SZ, TZ, Carlsbad, California 9201 1 (US). -

The San Diego Business Journal Digital Edition
labusinessjournal.com LOSANGELESBUSINESS JOURNAL THE COMMUNITY OF BUSINESS TM sfvbj.com SAN FERNANDOVALLEY BUSINESS JOURNAL LOS ANGELES • GLENDALE • SANTA CLARITA VALLEY • BURBANK • CONEJO VALLEY • SIMI VALLEY • SAN FERNANDO • CALABASAS • AGOURA HILLS • ANTELOPE VALLEY THE COMMUNITY OF BUSINESS TM sfvbj.com BUSINESS AN ERNANDO ALLEY JOURNAL SLOS ANGELES • GLENDALEF • SANTA CLARITA VALLEY • BURBANK • CONEJO VALLEY • SIMI VALLEY V• SAN FERNANDO • CALABASAS • AGOURA HILLS • ANTELOPE VALLEY THE COMMUNITY OF BUSINESS TM ocbj.com ORANGE COUNTY BUSINESS JOURNAL THE COMMUNITY OF BUSINESS TM Thumbnails SDBJ User Guide Front Page Table of Contents sdbj.com SAN DIEGO BUSINESS JOURNAL DIGITAL EDITION THE COMMUNITY OF BUSINESSTM www.sdbj.com/digital WELCOME TO THE SAN DIEGO BUSINESS JOURNAL DIGITAL EDITION To read your copy of the Digital Edition INSTRUCTION Please select a reading preference FOR PC/MAC How to read SDBJ Digital Edition on iPad in iBooks: 1 TAP CENTER 2 TAP ‘OPEN WITH’ 3 TAP ‘iBOOKS’ Wait for gray bar with Wait for scroll down menu buttons to appear menu and tap the iBooks on top of the PDF. icon. Wait for PDF to load in iBOOKS. Thumbnails SDBJ User Guide Front Page Table of Content sdbj.com SAN DIEGO BUSINESS JOURNAL Volume 32, Number 15 THE COMMUNITY OF BUSINESSTM April 11-17, 2011 $2.00 Real Estate 3FOBUB4JNSJMPG +POFT-BOH-B4BMMF TBZTTPNFGFEFSBM BHFODJFTBSFTFFLJOH PRODUCTS OF OUR NPSFPGàDFTQBDFJO 4BO%JFHP Page 10 ENVIRONMENT Rubio’s “does a really good job Public Relations , agrees that the Housing MARKETING: Region’s of owning something,” said Daniel name Rubio’s goes with the phrase Famous Brands Include Khabie , founder and chief executive “fi sh taco.” “ ‘McDonald’s Fish Taco’ offi cer of Digitaria Interactive Inc.