DOCSLIB.ORG

3D Modeling: Surfaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
3D Modeling: Surfaces CS 430/536 Computer Graphics I Overview • 3D model representations 3D Modeling: • Mesh formats Surfaces • Bicubic surfaces • Bezier surfaces Week 8, Lecture 16 • Normals to surfaces David Breen, William Regli and Maxim Peysakhov • Direct surface rendering Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel University 1 2 http://gicl.cs.drexel.edu 1994 Foley/VanDam/Finer/Huges/Phillips ICG 3D Modeling Representing 3D Objects • 3D Representations • Exact • Approximate – Wireframe models – Surface Models – Wireframe – Facet / Mesh – Solid Models – Parametric • Just surfaces – Meshes and Polygon soups – Voxel/Volume models Surface – Voxel – Decomposition-based – Solid Model • Volume info • Octrees, voxels • CSG • Modeling in 3D – Constructive Solid Geometry (CSG), • BRep Breps and feature-based • Implicit Solid Modeling 3 4 Negatives when Representing 3D Objects Representing 3D Objects • Exact • Approximate • Exact • Approximate – Complex data structures – Lossy – Precise model of – A discretization of – Expensive algorithms – Data structure sizes can object topology the 3D object – Wide variety of formats, get HUGE, if you want each with subtle nuances good fidelity – Mathematically – Use simple – Hard to acquire data – Easy to break (i.e. cracks represent all primitives to – Translation required for can appear) rendering – Not good for certain geometry model topology applications • Lots of interpolation and and geometry guess work 5 6 1 Positives when Exact Representations Representing 3D Objects • Exact • Approximate • Wireframe – Precision – Easy to implement • Simulation, modeling, • Parametric Surface etc – Easy to acquire – Lots of modeling • 3D scanner, CT • Solid Model environments – Physical properties – Easy to render – operations – Many applications (tool • Direct mapping to the path generation, motion, graphics pipeline – CSG, BRep, implicit geometry etc.) – Lots of algorithms – Compact 7 8 Wireframes Issues with Wireframes • Basic idea: • Visually ambiguous – Represent the model • No surfaces! as the set of all of its – What’s inside? What’s outside? edges – Hidden line removal? • What does validity entail? • Example: – Don’t we just have a bunch of wires? A simple cube – Do they need to add up to something? – 12 lines • How to model wireframe shapes? – 8 vertices – Wire by wire? Not very easy! • How about the faces? 9 11 Foley/VanDam, 1990/1994 Surface Models 3D Mesh File Formats • Basic idea: Some common formats – Represent a model as a set of • STL faces/patches • Limitations: • SMF – Topological integrity; how do faces “line up”?; which way is ‘inside’/ ‘outside’? • OpenInventor • Used in many CAD applications • VRML – Why? They are fine for drafting and rendering, not as good for creating true physical models 12 13 2 Minimal Full-Featured • Vertex + Face • Colors / Transparency • Vertex-Face Normals (optional, can be computed) • No colors, normals, • Scene Graph or texture • Lights • Textures • Primarily used to • Views and Navigation demonstrate geometry algorithms 14 15 Simple Mesh Format (SMF) Stereolithography (STL) • Michael Garland http://graphics.cs.uiuc.edu/~garland/ • Triangle data + Face Normal • Triangle data • The de-facto standard for rapid prototyping • Vertex indices begin at 1 16 17 How STL Works Open Inventor • Developed by SGI • Predecessor to VRML – Scene Graph 18 20 3 Virtual Reality Modeling Issues with 3D “mesh” formats Language (VRML) • Easy to acquire • SGML Based • Easy to render • Harder to model with • Scene-Graph • Error prone – split faces, holes, gaps, etc • Full Featured 21 22 BRep Data Structure BRep Data Structures • Vertex structure • Winged-Edge Data – X,Y,Z point Structure (Weiler) – Pointers to n coincident edges • Vertex • Edge structure – 2 pointers to end-point vertices – n edges – 2 pointers to adjacent faces • Edge – Pointer to next edge – 2 vertices – Pointer to previous edge – 2 faces • Face structure • Face – Pointers to m edges – m edges 23 24 Pics/Math courtesy of Dave Mount @ UMD-CP Biparametric Surfaces Bicubic Surfaces • Biparametric surfaces • Recall the 2D curve: – A generalization of parametric curves – G: Geometry Matrix – 2 parameters: s, t (or u, v) – M: Basis Matrix – Two parametric functions – S: Polynomial Terms [s3 s2 s 1] • For 3D, we allow the points in G to vary in 3D along t as well: 25 26 4 Observations About Bicubic Surfaces Bicubic Surfaces • For a fixed t1, • Each is , where is a curve • Gradually incrementing t1 to t2, we get a new curve • Transposing , we get • The combination of these curves is a surface • are 3D curves 27 28 Bicubic Surfaces Bicubic Surfaces • Substituting into , • Writing out we get Q(s, t) gives • The g11, etc. are the control points for the Bicubic surface patch: 29 30 Faceting Bézier Surfaces • Bézier Surfaces (similar definition) 32 33 5 Plotting Isolines Faceting 34 35 Bézier Surfaces: Example Bézier Surfaces • C0 and G0 continuity can be achieved between two patches by setting • Utah Teapot the 4 boundary modeled by 32 control points to be Bézier Patches with equal G1 continuity • G1 continuity achieved when cross-wise CPs are co-linear 36 37 Bezier Surface: Example B-spline Surfaces • Increased facet resolution • Rendered • Representation for B-spline patches • C2 continuity across boundaries is automatic with B-splines 38 39 6 Computing the Normals to Surfaces Normals to Surfaces • Normals used for • For a bicubic surface, – Shading first, compute the s tangent vector – Interference detection in robotics – Calculating offsets for numerically controlled machining 40 41 Computing the Computing the Normals to Surfaces Normals to Surfaces • Next, compute the t tangent vector: • Since s and t are tangent to the surface, their cross product is the normal vector to the surface! t • xs - x component of s tangent • ys - y component of s tangent • z - z component of s tangent 42 s 43 Drawing Parametric Surfaces Direct Rendering • Usually done “patch by patch” • Use a scan-line algorithm • Two choices – Evaluate pixel by pixel – Draw/render directly from the parametric – Problem: How to go from (x,y) “screen description space” to point on the 3D patch – Approximate the surface with a polygon • Easy for a planar polygon where we know max/min y, equations for edges, screen depth mesh, then draw/render the mesh • Not as easy for parametric surfaces 45 46 7 Direct Scan Conversion of Issues for Direct Rendering Patches • Max/Min y coords may not lie on boundaries • Basic idea • Silhouette edges result from patch bulges – Find intersection of – Need to track both silhouettes and boundaries patch with XZ plane • What if they intersect? • Producing a planar curve • Note: patch edges need not be monotonic in x or y – Draw the curve • De Boor, D’Casteljeau • Idea: Scan convert patch plane-by-plane, using scan planes instead of scan lines – Note: if doing rendering, one can compute pixel- by-pixel color values this way 47 – Patch: x=X(u,v), y=Y(u,v), z=Z(u,v) 48 Object Space Conversion: Patch to Polygon Conversion Uniform Subdivision Two methods: Basic Procedure • Object Space Conversion • Cut parameter space into equal parts – Techniques • Uniform subdivision • Find new points on the surface • Non-uniform subdivision – Resolution: depends on object space • Recurse/Repeat “until done” • Image Space Conversion • Split squares into – Resolution: depends on pixels and screen triangles • Render 50 51 Object Space Conversion: Image Space Conversion Non-Uniform Subdivision • Basic idea • Idea: control subdivision based on – More facets in areas of high curvature screen criteria – Use change in normals to surface to – Minimum pixel area assess curvature • Stop when patch is basically one pixel • More derivatives – Screen flatness – Break patch into sub-patches based on • Stop when patch converges to a polygon curvature changes – Screen flatness of silhouette edges • Stop when edge is straight or size of pixel 52 53 8 How do I know if I’ve found a silhouette edge? • If the viewing ray is tangent to the surface at the point it hits the surface! N • L = 0 – Where N is the normal at the point where L, the line of sight, hits the surface 54 9.
Load more

Recommended publications
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
  • Surface Physics I and II
    Surface physics I and II Lectures: Mon 12-14 ,Wed 12-14 D116 Excercises: TBA Lecturer: Antti Kuronen, [email protected] Exercise assistant: Ane Lasa, [email protected] Course homepage: http://www.physics.helsinki.fi/courses/s/pintafysiikka/ Objectives ● To study properties of surfaces of solid materials. ● The relationship between the composition and morphology of the surface and its mechanical, chemical and electronic properties will be dealt with. ● Technologically important field of surface and thin film growth will also be covered. Surface physics I 2012: 1. Introduction 1 Surface physics I and II ● Course in two parts ● Surface physics I (SPI) (530202) ● Period III, 5 ECTS points ● Basics of surface physics ● Surface physics II (SPII) (530169) ● Period IV, 5 ECTS points ● 'Special' topics in surface science ● Surface and thin film growth ● Nanosystems ● Computational methods in surface science ● You can take only SPI or both SPI and SPII Surface physics I 2012: 1. Introduction 2 How to pass ● Both courses: ● Final exam 50% ● Exercises 50% ● Exercises ● Return by ● email to [email protected] or ● on paper to course box on the 2nd floor of Physicum ● Return by (TBA) Surface physics I 2012: 1. Introduction 3 Table of contents ● Surface physics I ● Introduction: What is a surface? Why is it important? Basic concepts. ● Surface structure: Thermodynamics of surfaces. Atomic and electronic structure. ● Experimental methods for surface characterization: Composition, morphology, electronic properties. ● Surface physics II ● Theoretical and computational methods in surface science: Analytical models, Monte Carlo and molecular dynamics sumilations. ● Surface growth: Adsorption, desorption, surface diffusion. ● Thin film growth: Homoepitaxy, heteroepitaxy, nanostructures.
    [Show full text]
  • Luna Moth: Supporting Creativity in the Cloud
    Pedro Alfaiate Instituto Superior Técnico / Luna Moth INESC-ID Inês Caetano Instituto Superior Técnico / INESC-ID Supporting Creativity in the Cloud António Leitão Instituto Superior Técnico / INESC-ID 1 ABSTRACT Algorithmic design allows architects to design using a programming-based approach. Current algo- 1 Migration from desktop application rithmic design environments are based on existing computer-aided design applications or building to the cloud. information modeling applications, such as AutoCAD, Rhinoceros 3D, or Revit, which, due to their complexity, fail to give architects the immediate feedback they need to explore algorithmic design. In addition, they do not address the current trend of moving applications to the cloud to improve their availability. To address these problems, we propose a software architecture for an algorithmic design inte- grated development environment (IDE), based on web technologies, that is more interactive than competing algorithmic design IDEs. Besides providing an intuitive editing interface which facilitates programming tasks for architects, its performance can be an order of magnitude faster than current aalgorithmic design IDEs, thus supporting real-time feedback with more complex algorithmic design programs. Moreover, our solution also allows architects to export the generated model to their preferred computer-aided design applications. This results in an algorithmic design environment that is accessible from any computer, while offering an interactive editing environment that inte- grates into the architect’s workflow. 72 INTRODUCTION programming languages that also support traceability between Throughout the years, computers have been gaining more ground the program and the model: when the user selects a component in the field of architecture. In the beginning, they were only used in the program, the corresponding 3D model components are for creating technical drawings using computer-aided design highlighted.
    [Show full text]
  • Surface Water
    Chapter 5 SURFACE WATER Surface water originates mostly from rainfall and is a mixture of surface run-off and ground water. It includes larges rivers, ponds and lakes, and the small upland streams which may originate from springs and collect the run-off from the watersheds. The quantity of run-off depends upon a large number of factors, the most important of which are the amount and intensity of rainfall, the climate and vegetation and, also, the geological, geographi- cal, and topographical features of the area under consideration. It varies widely, from about 20 % in arid and sandy areas where the rainfall is scarce to more than 50% in rocky regions in which the annual rainfall is heavy. Of the remaining portion of the rainfall. some of the water percolates into the ground (see "Ground water", page 57), and the rest is lost by evaporation, transpiration and absorption. The quality of surface water is governed by its content of living organisms and by the amounts of mineral and organic matter which it may have picked up in the course of its formation. As rain falls through the atmo- sphere, it collects dust and absorbs oxygen and carbon dioxide from the air. While flowing over the ground, surface water collects silt and particles of organic matter, some of which will ultimately go into solution. It also picks up more carbon dioxide from the vegetation and micro-organisms and bacteria from the topsoil and from decaying matter. On inhabited watersheds, pollution may include faecal material and pathogenic organisms, as well as other human and industrial wastes which have not been properly disposed of.
    [Show full text]
  • Surface Topology
    2 Surface topology 2.1 Classification of surfaces In this second introductory chapter, we change direction completely. We dis- cuss the topological classification of surfaces, and outline one approach to a proof. Our treatment here is almost entirely informal; we do not even define precisely what we mean by a ‘surface’. (Definitions will be found in the following chapter.) However, with the aid of some more sophisticated technical language, it not too hard to turn our informal account into a precise proof. The reasons for including this material here are, first, that it gives a counterweight to the previous chapter: the two together illustrate two themes—complex analysis and topology—which run through the study of Riemann surfaces. And, second, that we are able to introduce some more advanced ideas that will be taken up later in the book. The statement of the classification of closed surfaces is probably well known to many readers. We write down two families of surfaces g, h for integers g ≥ 0, h ≥ 1. 2 2 The surface 0 is the 2-sphere S . The surface 1 is the 2-torus T .For g ≥ 2, we define the surface g by taking the ‘connected sum’ of g copies of the torus. In general, if X and Y are (connected) surfaces, the connected sum XY is a surface constructed as follows (Figure 2.1). We choose small discs DX in X and DY in Y and cut them out to get a pair of ‘surfaces-with- boundaries’, coresponding to the circle boundaries of DX and DY.
    [Show full text]
  • Full Body 3D Scanning
    3D Photography: Final Project Report Full Body 3D Scanning Sam Calabrese Abhishek Gandhi Changyin Zhou fsmc2171, asg2160, [email protected] Figure 1: Our model is a dancer. We capture his full-body 3D model by combining image-based methods and range scanner, and then do an animation of dancing. Abstract Compared with most laser scanners, image-based methods using triangulation principles are much faster and able to provide real- In this project, we are going to build a high-resolution full-body time 3D sensing. These methods include depth from motion [Aloi- 3D model of a live person by combining image-based methods and monos and Spetsakis 1989], shape from shading [Zhang et al. laser scanner methods. A Leica 3D range scanner is used to obtain 1999], depth from defocus/focus [Nayar et al. 1996][Watanabe and four accurate range data of the body from four different perspec- Nayar 1998][Schechner and Kiryati 2000][Zhou and Lin 2007], and tives. We hire a professional model and adopt many measures to structure from stereo [Dhond and Aggarwal 1989]. They often re- minimize the movement during the long laser-scanning. The scan quire the object surface to be textured, non-textured, or lambertian. data is then sequently processed by Cyclone, MeshLab, Scanalyze, These requirements often make them impractical in many cases. VRIP, PlyCrunch and 3Ds Max to obtain our final mesh. We take In addition, image-based methods usually cannot give a precision three images of the face from frontal and left/right side views, and depth estimation since they do patch-based analysis.
    [Show full text]
  • Differential Geometry of Curves and Surfaces 3
    DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 3. Regular Surfaces 3.1. The definition of a regular surface. Examples. The notion of surface we are going to deal with in our course can be intuitively understood as the object obtained by a potter full of phantasy who takes several pieces of clay, flatten them on a table, then models of each of them arbitrarily strange looking pots, and finally glue them together and flatten the possible edges and corners. The resulting object is, formally speaking, a subset of the three dimensional space R3. Here is the rigorous definition of a surface. Definition 3.1.1. A subset S ⊂ R3 is a1 regular surface if for any point P in S one can find an open subspace U ⊂ R2 and a map ϕ : U → S of the form ϕ(u, v)=(x(u, v),y(u, v), z(u, v)), for (u, v) ∈ U with the following properties: 1. The function ϕ is differentiable, in the sense that the components x(u, v), y(u, v) and z(u, v) have partial derivatives of any order. 2 3 2. For any Q in U, the differential map d(ϕ)Q : R → R is (linear and) injective. 3. There exists an open subspace V ⊂ R3 which contains P such that ϕ(U) = V ∩ S and moreover, ϕ : U → V ∩ S is a homeomorphism2. The pair (U, ϕ) is called a local parametrization, or a chart, or a local coordinate system around P . Conditions 1 and 2 say that (U, ϕ) is a regular patch.
    [Show full text]
  • Mostly Surfaces
    Mostly Surfaces Richard Evan Schwartz ∗ August 21, 2011 Abstract This is an unformatted version of my book Mostly Surfaces, which is Volume 60 in the A.M.S. Student Library series. This book has the same content as the published version, but the arrangement of some of the text and equations here is not as nice, and there is no index. Preface This book is based on notes I wrote when teaching an undergraduate seminar on surfaces at Brown University in 2005. Each week I wrote up notes on a different topic. Basically, I told the students about many of the great things I have learned about surfaces over the years. I tried to do things in as direct a fashion as possible, favoring concrete results over a buildup of theory. Originally, I had written 14 chapters, but later I added 9 more chapters so as to make a more substantial book. Each chapter has its own set of exercises. The exercises are embedded within the text. Most of the exercises are fairly routine, and advance the arguments being developed, but I tried to put a few challenging problems in each batch. If you are willing to accept some results on faith, it should be possible for you to understand the material without working the exercises. However, you will get much more out of the book if you do the exercises. The central object in the book is a surface. I discuss surfaces from many points of view: as metric spaces, triangulated surfaces, hyperbolic surfaces, ∗ Supported by N.S.F.
    [Show full text]
  • Bonus Ch. 2 More Modeling Techniques
    Bonus Ch. 2 More Modeling Techniques When it comes to modeling in modo, the sky is the limit. This book is designed to show you all of the techniques available to you, through written word and visual examples on the DVD. This chapter will take you into another project, in which you’ll model a landscape. From there, you’ll texture it, and later you’ll add the environment. You’ll see how modo’s micro polygon displacement works and how powerful it is. From there, you’ll create a cool toy gun. The techniques used in this project will show you how to create small details that make the model come to life. Then, you’ll learn to texture the toy gun to look like real plastic. Building a Landscape Landscapes traditionally have been a chore for 3D artists. This is because to prop- erly create them, you need a lot of geometry. A lot of geometry means a lot of polygons, and a lot of polygons means a lot of render time. But the team at Luxology has introduced micro polygon displacement in modo 201/202, allow- ing you to create and work with simple objects, but render with millions of poly- gons. How is this possible? The micro polygon displacement feature generates additional polygons at render time. The goal is that finer details can be achieved without physically modeling them into the base object. You can then add to the details achieved through micro poly displacements with modo’s bump map capabilities and generate some terrific-looking models.
    [Show full text]
  • Basics of the Differential Geometry of Surfaces
    Chapter 20 Basics of the Differential Geometry of Surfaces 20.1 Introduction The purpose of this chapter is to introduce the reader to some elementary concepts of the differential geometry of surfaces. Our goal is rather modest: We simply want to introduce the concepts needed to understand the notion of Gaussian curvature, mean curvature, principal curvatures, and geodesic lines. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate differential geometry course offered in the fall of 1994. Most of the topics covered in this course have been included, except a presentation of the global Gauss–Bonnet–Hopf theorem, some material on special coordinate systems, and Hilbert’s theorem on surfaces of constant negative curvature. What is a surface? A precise answer cannot really be given without introducing the concept of a manifold. An informal answer is to say that a surface is a set of points in R3 such that for every point p on the surface there is a small (perhaps very small) neighborhood U of p that is continuously deformable into a little flat open disk. Thus, a surface should really have some topology. Also,locally,unlessthe point p is “singular,” the surface looks like a plane. Properties of surfaces can be classified into local properties and global prop- erties.Intheolderliterature,thestudyoflocalpropertieswascalled geometry in the small,andthestudyofglobalpropertieswascalledgeometry in the large.Lo- cal properties are the properties that hold in a small neighborhood of a point on a surface. Curvature is a local property. Local properties canbestudiedmoreconve- niently by assuming that the surface is parametrized locally.
    [Show full text]
  • Surface Details
    Surface Details ✫ Incorp orate ne details in the scene. ✫ Mo deling with p olygons is impractical. ✫ Map an image texture/pattern on the surface Catmull, 1974; Blin & Newell, 1976. ✫ Texture map Mo dels patterns, rough surfaces, 3D e ects. ✫ Solid textures 3D textures to mo del wood grain, stains, marble, etc. ✫ Bump mapping Displace normals to create shading e ects. ✫ Environment mapping Re ections of environment on shiny surfaces. ✫ Displacement mapping Perturb the p osition of some pixels. CPS124, 296: Computer Graphics Surface Details Page 1 Texture Maps ✫ Maps an image on a surface. ✫ Each element is called texel. ✫ Textures are xed patterns, pro cedurally gen- erated, or digitized images. CPS124, 296: Computer Graphics Surface Details Page 2 Texture Maps ✫ Texture map has its own co ordinate system; st-co ordinate system. ✫ Surface has its own co ordinate system; uv -co ordinates. ✫ Pixels are referenced in the window co ordinate system Cartesian co ordinates. Texture Space Object Space Image Space (s,t) (u,v) (x,y) CPS124, 296: Computer Graphics Surface Details Page 3 Texture Maps v u y xs t s x ys z y xs t s x ys z CPS124, 296: Computer Graphics Surface Details Page 4 Texture Mapping CPS124, 296: Computer Graphics Surface Details Page 5 Texture Mapping Forward mapping: Texture scanning ✫ Map texture pattern to the ob ject space. u = f s; t = a s + b t + c; u u u v = f s; t = a s + b t + c: v v v ✫ Map ob ject space to window co ordinate sys- tem. Use mo delview/pro jection transformations.
    [Show full text]
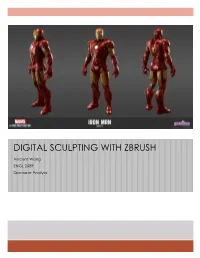
  • Digital Sculpting with Zbrush
    DIGITAL SCULPTING WITH ZBRUSH Vincent Wang ENGL 2089 Discourse Analysis 2 ZBrush Analysis Table of Contents Context ........................................................................................................................... 3 Process ........................................................................................................................... 5 Analysis ........................................................................................................................ 13 Application .................................................................................................................. 27 Activity .......................................................................................................................... 32 Works Cited .................................................................................................................. 35 3 Context ZBrush was created by the Pixologic Inc., which was founded by Ofer Alon and Jack Rimokh (Graphics). It was first presented in 1999 at SIGGRAPH (Graphics). Version 1.5 was unveiled at the MacWorld Expo 2002 in New York and SIGGRAPH 2002 in San Antonio (Graphics). Pixologic, the company describes the 3D modeling software as a “digital sculpting and painting program that has revolutionized the 3D industry…” (Pixologic). It utilizes familiar real-world tools in a digital environment, getting rid of steep learning curves and allowing the user to be freely creative instead of figuring out all the technical details. 3D models that are created in
    [Show full text]