Reasoning About Knowledge and Action in Cluedo Using Prolog
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Point Redemption Form - Europe (Euros)
POINT REDEMPTION FORM - EUROPE (EUROS) Qty Product Unit Points Qty Product Unit Points Oil Singles Thyme 15 ml 37,50 Arborvitae 5 ml 27,00 Turmeric 15 ml 31,50 Basil 15 ml 21,50 Vetiver 15 ml 47,00 Bergamot 15 ml 31,50 Wild Orange 15 ml 11,50 Black Pepper 5 ml 22,00 Wintergreen 15 ml 25,50 Black Spruce 5 ml n/a Yarrow | POM 30 ml 106,50 Blue Tansy 5 ml 107,00 Ylang Ylang 15 ml 44,00 Cardamom 5 ml 31,50 Oil Blends Cassia 15 ml 20,00 dōTERRA Adaptiv™ 15 ml 42,00 Cedarwood 15 ml 15,00 dōTERRA Adaptiv™ Touch 10 ml 22,50 Celery Seed 15 ml 40,50 dōTERRA Air™ 15 ml 21,75 Cilantro 15 ml 27,50 dōTERRA Air™ Touch 10 ml 14,00 Cinnamon 5 ml 22,50 dōTERRA Align 5 ml 17,00 Citronella 15 ml 20,50 dōTERRA Anchor 5 ml 22,00 Clary Sage 15 ml 39,00 dōTERRA Arise 5 ml 19,00 Clove 15 ml 15,00 AromaTouch™ 15 ml 28,00 Copaiba 15 ml 39,00 dōTERRA Balance™ 15 ml 25,00 Coriander 15 ml 27,50 Balance Touch 10 ml n/a Cypress 15 ml 17,00 dōTERRA Brave™ 10 ml 23,50 Douglas Fir 5 ml 25,00 dōTERRA Calmer™ 10 ml 21,50 Eucalyptus 15 ml 15,00 dōTERRA Cheer™ 5 ml 26,50 Fennel (Sweet) 15 ml 16,00 dōTERRA Cheer™ Touch 10 ml 18,00 Frankincense 15 ml 75,00 Citrus Bliss™ 15 ml 25,00 dōTERRA Frankincense Touch 10 ml 47,00 ClaryCalm™ Roll-On 10 ml 27,25 Geranium 15 ml 37,50 dōTERRA Console™ 5 ml 40,00 Ginger 15 ml 42,00 dōTERRA Console™ Touch 10 ml 26,50 Grapefruit 15 ml 17,00 DDR Prime™ 15 ml 31,50 Green Mandarin 15 ml 31,50 DDR Prime™ Softgels 60 Sgls 62,50 Helichrysum 5 ml 94,00 Deep Blue™ 5 ml 37,50 Helichrysum Touch 10 ml n/a Deep Blue™ Roll-On 10 ml 75,00 Jasmine Touch 10 -

Season Eight of My Little Pony: Friendship Is Magic Premieres Saturday, March 24 on Discovery Family
FOR IMMEDIATE RELEASE February 8, 2018 CONTACT: Jared Albert, (786) 273-4476 [email protected] THE SCHOOL OF FRIENDSHIP IS OFFICIALLY OPEN! SEASON EIGHT OF MY LITTLE PONY: FRIENDSHIP IS MAGIC PREMIERES SATURDAY, MARCH 24 ON DISCOVERY FAMILY – Season Eight of “My Little Pony: Friendship is Magic” Picks Up Following the Events of “My Little Pony: The Movie” with New Characters and Songs Throughout 26 Magical Episodes Beginning Saturday, March 24 at 11:30a/10:30c – (Miami, FL) – Calling everypony (and creature) in Equestria -- Twilight Sparkle’s School of Friendship is in session! On Saturday, March 24 at 11:30a/10:30c, Discovery Family premieres the eighth season of MY LITTLE PONY: FRIENDSHIP IS MAGIC with 26 half hour episodes complete with seven original songs, new characters and tons of friendship! New episodes of the Hasbro Studios’ produced animated series will also stream live and on demand on Discovery Family GO, the network’s TV Everywhere app. Following the events of “My Little Pony: The Movie,” in the back-to-back season premiere episodes titled “School Daze Part 1” and “School Daze Part 2,” the Mane 6 discovers that the Friendship Map has expanded to show the world outside Equestria. Through two exciting original songs, Twilight Sparkle learns that friendship needs to spread beyond the limits of the kingdom and decides to open her very own School of Friendship. But things come to a head when the new non-pony students ditch class on Friends and Family day, putting the entire school in jeopardy! This season, viewers will witness major milestones featuring the introduction of Starlight Glimmer’s parents and Princess Celestia's big acting debut. -

Covid-19 Positive Case List (From 1 July Onwards) Accreditation Holder
Covid-19 Positive Case List (From 1 July onwards) Accreditation holder As of 17-Jul-21 Harumi OV/PV Date of Date of positive Residents/Non-residents of Under/After 14-day Prefecture that Residents/Non-residents No Category Notes announcement case reported Japan quarantine period reported the case Residents Non-residents This case was already announced as No.67 case in the previous list that has 1 02-Jul-21 29-Jun-21 Residents of Japan N/A Tokyo 2020 Contractor Tokyo ✔ been updated till 2 July. This case was already announced as No.68 case in the previous list that has 2 02-Jul-21 01-Jul-21 Residents of Japan N/A Tokyo 2020 employee Tokyo ✔ been updated till 2 July. 3 05-Jul-21 02-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor To be confirmed ✔ 4 05-Jul-21 01-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Tokyo ✔ 5 05-Jul-21 02-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Tokyo ✔ 6 05-Jul-21 02-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Chiba ✔ 7 05-Jul-21 02-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor To be confirmed ✔ 8 05-Jul-21 03-Jul-21 Residents of Japan N/A Media Tokyo ✔ 9 05-Jul-21 03-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Tokyo ✔ 10 06-Jul-21 02-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Tokyo ✔ 11 06-Jul-21 04-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Hokkaido ✔ 12 06-Jul-21 03-Jul-21 Residents of Japan N/A Tokyo 2020 Contractor Chiba ✔ 13 07-Jul-21 06-Jul-21 Residents of Japan N/A Tokyo 2020 employee Chiba ✔ 14 07-Jul-21 05-Jul-21 Residents of Japan N/A Games-concerned -

The Complete Guide to Social Media from the Social Media Guys
The Complete Guide to Social Media From The Social Media Guys PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Mon, 08 Nov 2010 19:01:07 UTC Contents Articles Social media 1 Social web 6 Social media measurement 8 Social media marketing 9 Social media optimization 11 Social network service 12 Digg 24 Facebook 33 LinkedIn 48 MySpace 52 Newsvine 70 Reddit 74 StumbleUpon 80 Twitter 84 YouTube 98 XING 112 References Article Sources and Contributors 115 Image Sources, Licenses and Contributors 123 Article Licenses License 125 Social media 1 Social media Social media are media for social interaction, using highly accessible and scalable publishing techniques. Social media uses web-based technologies to turn communication into interactive dialogues. Andreas Kaplan and Michael Haenlein define social media as "a group of Internet-based applications that build on the ideological and technological foundations of Web 2.0, which allows the creation and exchange of user-generated content."[1] Businesses also refer to social media as consumer-generated media (CGM). Social media utilization is believed to be a driving force in defining the current time period as the Attention Age. A common thread running through all definitions of social media is a blending of technology and social interaction for the co-creation of value. Distinction from industrial media People gain information, education, news, etc., by electronic media and print media. Social media are distinct from industrial or traditional media, such as newspapers, television, and film. They are relatively inexpensive and accessible to enable anyone (even private individuals) to publish or access information, compared to industrial media, which generally require significant resources to publish information. -

\\ Investment Highlights Business Description Market Cap. $11.41B P
Consumer Discretionary Sector, Toy and Game Industry NASDAQ Stock Exchange \\ Hasbro Inc. Date: 04/16/2018 Current Price: $88.26 (04/16/2018) Recommendation: BUY Ticker - NASDAQ: HAS Headquarters: Pawtucket, RI Target Price: $112.69 (27.7% Upside) Investment Highlights Figure 1 – Share Price We recommend a BUY rating for Hasbro Inc. based on a 1-year target price of $112.69 per share. Our target price offers a 27.7% margin of safety based on its closing price of $88.26 on April 16, 2018. The following factors are the main drivers of our investment recommendation: Strong Industry Outlook & Positioning The global Toy and Game industry is poised for consistent growth in both developed and emerging markets, and the Digital Gaming and Entertainment space is expanding rapidly. Hasbro’s brand portfolio and strategy effectively places it at the center of this growth. Brand Storytelling Source: Bloomberg Hasbro’s strongest asset is their ability to tell stories that drive engagement and grow their brands. Its ability to leverage its ecosystem of products, content, and media to create emotional connections and drive engagement make it a standout. Figure 2 – Valuation Weighting Industry Leading Brand Portfolio Base Case Valuation Hasbro possesses an industry leading entertainment and play brand portfolio especially suited to a DCF 50% $ 102.43 broad range of users. Other industry players have struggled with, or have just began creating such Comps 50% $ 122.94 a portfolio. Price Per Share $ 112.69 Margin of Safety @ 88.26 27.7% Effective Multi-Platform Brand Strategy Source: Company Data + Team Analysis Hasbro’s Brand Blueprint and “Share of Life” strategy has allowed it to expand the profitability and earning potential of its brand portfolio by leveraging film, television and digital gaming media in addition to traditional toys and games. -

Hasbro 2021 Investor Event Transcript
REFINITIV STREETEVENTS EDITED TRANSCRIPT HAS.OQ - Hasbro Inc Investor Event 2021 EVENT DATE/TIME: FEBRUARY 25, 2021 / 3:00PM GMT REFINITIV STREETEVENTS | www.refinitiv.com | Contact Us ©2021 Refinitiv. All rights reserved. Republication or redistribution of Refinitiv content, including by framing or similar means, is prohibited without the prior written consent of Refinitiv. 'Refinitiv' and the Refinitiv logo are registered trademarks of Refinitiv and its affiliated companies. FEBRUARY 25, 2021 / 3:00PM, HAS.OQ - Hasbro Inc Investor Event 2021 CORPORATE PARTICIPANTS Brian D. Goldner Hasbro, Inc. - Chairman & CEO Casey Collins Hasbro, Inc. - Senior VP & GM of Consumer Products Chris Cocks Wizards of the Coast LLC - President Darren Dennis Throop Entertainment One Ltd. - CEO, President & Director Debbie Hancock Hasbro, Inc. - SVP of IR Deborah M. Thomas Hasbro, Inc. - Executive VP & CFO Eric C. Nyman Hasbro, Inc. - Chief Consumer Officer Kathrin Belliveau Hasbro, Inc. - Senior VP & Chief Purpose Officer Kim Boyd Hasbro, Inc. - Senior Vice President & General Manager of Global Brands Olivier Dumont Entertainment One Ltd. - President of Family Brands Steve Bertram Entertainment One Ltd. - President of Film & Television CONFERENCE CALL PARTICIPANTS Arpine Kocharyan UBS Investment Bank, Research Division - Director and Analyst David James Beckel Joh. Berenberg, Gossler & Co. KG, Research Division - Analyst Eric Owen Handler MKM Partners LLC, Research Division - MD, Sector Head & Senior Analyst Frederick Charles Wightman Wolfe Research, LLC -
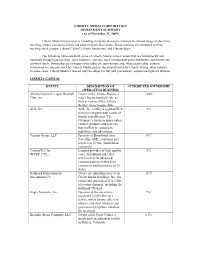
Asset List Effective 12-31-09
LIBERTY MEDIA CORPORATION INVESTMENT SUMMARY (As of December 31, 2009) Liberty Media Corporation is a holding company that owns interests in a broad range of electronic retailing, media, communications and entertainment businesses. Those interests are attributed to three tracking stock groups: Liberty Capital, Liberty Interactive, and Liberty Starz. The following table sets forth some of Liberty Media’s major assets that are held directly and indirectly through partnerships, joint ventures, common stock investments and instruments convertible into common stock. Ownership percentages in the table are approximate and, where applicable, assume conversion to common stock by Liberty Media and, to the extent known by Liberty Media, other holders. In some cases, Liberty Media’s interest may be subject to buy/sell procedures, repurchase rights or dilution. LIBERTY CAPITAL ENTITY DESCRIPTION OF ATTRIBUTED OWNERSHIP OPERATING BUSINESS Atlanta National League Baseball Owner of the Atlanta Braves, a 100% Club, Inc. major league baseball club, as well as certain of the Atlanta Braves' minor league clubs. AOL, Inc. AOL, Inc. (AOL) is a global Web 3% services company with a suite of brands and offerings. The Company’s business spans online content, products and services that it offers to consumers, publishers and advertisers. Current Group, LLC Provider of Broadband over 8%1 Powerline (BPL) solutions and services to electric distribution companies. CenturyTel, Inc. Leading provider of high-quality 2% (NYSE: CTL) voice, broadband and video services over its advanced communications networks to consumers and businesses in 33 states. Hallmark Entertainment Owner of controlling interest in 11%2 Investments Co. Crown Media Holdings, Inc., the owner and operator of U.S. -

LIBERTY MEDIA CORPORATION INVESTMENT SUMMARY (As of June 30, 2009)
LIBERTY MEDIA CORPORATION INVESTMENT SUMMARY (As of June 30, 2009) Liberty Media Corporation is a holding company that owns interests in a broad range of electronic retailing, media, communications and entertainment businesses. Those interests are attributed to three tracking stock groups: Liberty Capital, Liberty Interactive, and Liberty Entertainment. The following table sets forth some of Liberty Media’s major assets that are held directly and indirectly through partnerships, joint ventures, common stock investments and instruments convertible into common stock. Ownership percentages in the table are approximate and, where applicable, assume conversion to common stock by Liberty Media and, to the extent known by Liberty Media, other holders. In some cases, Liberty Media’s interest may be subject to buy/sell procedures, repurchase rights or dilution. LIBERTY CAPITAL ENTITY DESCRIPTION OF ATTRIBUTED OWNERSHIP OPERATING BUSINESS Atlanta National League Baseball Owner of the Atlanta Braves, a 100% Club, Inc. major league baseball club, as well as certain of the Atlanta Braves' minor league clubs. Current Group, LLC Provider of Broadband over 8%1 Powerline (BPL) solutions and services to electric distribution companies. Embarq Corporation Provider of a suite of 3% (NYSE: EQ) communications services to customers in its local services territories, including local and long distance voice, data, high speed internet, wireless and entertainment services. Hallmark Entertainment Owner of controlling interest in 11%2 Investments Co. Crown Media Holdings, Inc., the owner and operator of U.S. cable television channels, including the Hallmark Channel. Jingle Networks, Inc. Operator of the advertiser- 9%3 supported 1.800.FREE411 service which allows callers to obtain residential, business and government telephone numbers for no charge. -

Sony Reader PRS-500 Operation Guide
Browsing this Guide using Sony Reader Jumps to the table of contents Operation Guide PRS-500 Portable Reader System © 2006 Sony Corporation 2-680-300-01(1) About the Manuals Included with Sony Reader is the Quick Start Guide and this PDF-format Operation Guide. Additionally, after installing CONNECT Reader software from the supplied CD-ROM, you can refer to the Help within CONNECT Reader. Browsing the Operation Guide This PDF-format Operation Guide can be browsed on both your computer and Sony Reader. Browsing this Guide on your computer Click the Start menu in the bottom left of the Desktop, then select “All programs” – “CONNECT Reader” – “PRS-500 Operation Guide” to start Adobe Acrobat Reader and open the Operation Guide. For details on how to use Adobe Acrobat Reader, refer to the Adobe Acrobat Reader Help. Hint • To view the Operation Guide, you should have installed either Adobe Reader 5.0 or later. Adobe Reader can be downloaded for free from the Adobe website (www.adobe.com). 2 2-680-300-01(1) Browsing this Guide using Sony Reader From the Home menu, select “Books” – “Operation Guide” from the Book list. The Operation Guide can be opened by selecting “Option Menu” – “Begin.” PDF Link SIZE button Hints • A mark on this Guide indicates a link. Using the 5-way control button, press / to select the desired link, then press ENT to jump to the linked page. • To zoom in a page, press SIZE. For details on how to open books or PDF files, refer to page 32, 37. Using the CONNECT Reader Help Refer to the CONNECT Reader Help for details about using CONNECT Reader, such as importing books to your computer and transferring them to Sony Reader. -

Hasbro Advances Major Corporate Social Responsibility Priorities
Hasbro Advances Major Corporate Social Responsibility Priorities Including Eliminating Plastic in Packaging, Expanding Toy Recycling Program Globally and Furthering Environmental Assessments of Suppliers November 24, 2020 2019-20 Corporate Social Responsibility (CSR) Update Outlines Opportunities Following eOne Acquisition and Covers Response to COVID-19 PAWTUCKET, R.I.--(BUSINESS WIRE)--Nov. 24, 2020-- Hasbro, Inc. (NASDAQ: HAS) today issued a 2019-20 Corporate Social Responsibility Update. The update highlights Hasbro’s ESG advancements in key areas in 2019, reinforcing a multi-tiered strategy to directly engage employees, partner with governments and organizations to set and improve industry standards, and leverage supply chains to drive accountability. It also details Hasbro’s 2019 acquisition of eOne and the opportunities it unlocks for corporate citizenship through storytelling, content responsibility and social engagement. Most notably, the update details the company’s agile response to aligning its CSR priorities with the fast-changing environment globally, including the needs of various stakeholders amid the global pandemic and social unrest across the United States. This press release features multimedia. View the full release here: https://www.businesswire.com/news/home/20201124005635/en/ In 2019 and 2020, Hasbro took multiple actions to strengthen its commitment to the environment. Key milestones include: Establishing a goal to eliminate all plastic in packaging of new products by the end of 2022 Expanding the Hasbro Toy Recycling program to six countries Achieving its goal of virtually 100% renewable energy (99.4% through investment in renewable energy credits and carbon offsets). Additionally, Hasbro became the first in its industry to pilot the Higg Index, originally developed by the Sustainable Apparel Coalition (SAC), to further assess the environmental impact of its toy and game suppliers. -

INTERNATIONAL VOLLEYBALL FEDERATION (FIVB) Beach Volleyball
QUALIFICATION SYSTEM – GAMES OF THE XXXII OLYMPIAD – TOKYO 2020 INTERNATIONAL VOLLEYBALL FEDERATION (FIVB) Beach Volleyball A. EVENTS (2) Men’s Event (1) Women’s Event (1) 24-team tournament 24-team tournament B. ATHLETES QUOTA 1. Total Quota for Beach Volleyball: Tripartite Commission Qualification Places Host Country Places Total Invitation Places Men 46 (23 teams) 2 (1 team) - 48 (24 teams) Women 46 (23 teams) 2 (1 team) - 48 (24 teams) Total 92 (46 teams) 4 (2 teams) - 96 (48 teams) 2. Maximum Number of Athletes per NOC: Quota per NOC Men 4 (2 teams) Women 4 (2 teams) Total 8 (4 teams) 3. Type of Allocation of Quota Places: The quota place is allocated to the NOC. Each NOC must, upon recommendation of the respective National Federation, choose its athletes respecting the criteria set forth in section C. Athlete Eligibility. C. ATHLETE ELIGIBILITY All athletes must comply with the provisions of the Olympic Charter currently in force, including but not limited to, Rule 41 (Nationality of Competitors) and Rule 43 (World Anti-Doping Code and the Olympic Movement Code on the Prevention of Manipulation of Competitions). Only those athletes who comply with the Olympic Charter may participate in the Olympic Games Tokyo 2020. Age Requirements: The minimum age for a Beach Volleyball athlete is 14 years old, on the first day of the competition at the Olympic Games. All athletes participating in the Olympic Games Tokyo 2020 must therefore be born on/or before 25 July 2007. Original Version: ENGLISH 03 June 2021 Page 1/7 QUALIFICATION SYSTEM – GAMES OF THE XXXII OLYMPIAD – TOKYO 2020 Anti-Doping Requirements: The FIVB will only allow the registration of clean athletes who have been tested during the qualification period starting 1st June 2018 and ending 27th June 2021 (the “Qualification Period”). -

DVD+R on BDR-207D ・DVD+RW on BDR-207D ・CD-R on BDR-207D ・CD-RW on BDR-207D
Supported media list ・BD-R SL on BDR-207D ・BD-R DL TL on BDR-207D ・BD-RE on BDR-207D ・DVD-R on BDR-207D ・DVD-RW on BDR-207D ・DVD+R on BDR-207D ・DVD+RW on BDR-207D ・CD-R on BDR-207D ・CD-RW on BDR-207D FW:1.60 Supported media list of BDR-R SL on BDR-207D BD-R (2x format disc) Ver1.60 Writing speed : 2x Strategy Status No. Maker Manufacturer ID CAV CAV CAV CAV CAV Remarks 2x 4x 6x 4x 6x 8x 10x 12x 1 CMC "CMCMAGBA2" Y - - - - - - - 2 MAXELL "MAXELLRS1" Y - - - - - - - 8cm 3 Panasonic "MEI___T01" Y - - - - - - - 4 PHILIPS "PHILIPR02" Y - - - - - - - 5 RITEK "RITEK_BR1" Y - - - - - - - 6 SONY "SONY__NO1" Y - - - - - - - 7 SONY "SONY__NS1" Y - - - - - - - 8 TDK "TDKBLDRBA" Y - - - - - - - 9 TDK "TDKBLDRDA" Y - - - - - - - 8cm 10 MKM "VERBATIMa" Y - - - - - - - In case of unknown MID, the writing speed is limited to 2x. BD-R (LtoH 2x format disc) Writing speed : 2x Strategy Status No. Maker Manufacturer ID CAV CAV CAV CAV CAV Remarks 2x 4x 6x 4x 6x 8x 10x 12x 1 TAIYOYUDEN "TYG-BDY01" Y - - - - - - - 2 MKM "VERBATIMw" Y - - - - - - - In case of unknown MID, the writing speed is limited to 2x. BD-R (4x format disc) Writing speed : 2x, 4x, 6x, 8x, 10x, 12x Strategy Status No. Maker Manufacturer ID CAV CAV CAV CAV CAV Remarks 2x 4x 6x 4x 6x 8x 10x 12x 1 CMC "CMCMAGBA3" Y - - Y Y Y Y - 2 Daxon "Daxon_R4X" Y - - Y Y Y - - 3 Infomedia "INFOMER30" Y - - Y Y Y - - 4 Infosource "ISMMBDR01" Y - - Y Y Y - - 5 LGE "LGEBRAS04" Y - - Y Y Y - - 6 Panasonic "MEI___T02" Y - - Y Y Y Y - 7 Millenniata "MILLENMR1" Y Y - - - - - - 8 PHILIPS "PHILIPR04" Y - - Y Y Y Y - 9 PRODISC "PRODISCR0" Y - - Y Y Y Y - 10 RITEK "RITEK_BR2" Y - - Y Y Y Y - 11 SONY "SONY__NN2" Y - - Y Y Y Y Y 12 SONY "SONY__NS2" Y Y - - - - - - 13 TDK "TDKBLDRBB" Y - - Y Y Y Y - 14 Umedisc "UMEBDR014" Y - - Y Y Y - - 15 MKM "VERBATIMc" Y - - Y Y Y Y - In case of unknown MID, the writing speed is limited to 2x and 4x.