DOCSLIB.ORG

Polynomial, Rational, and Algebraic Expressions) 0.6.1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Polynomial, Rational, and Algebraic Expressions) 0.6.1 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES • Be able to identify polynomial, rational, and algebraic expressions. • Understand terminology and notation for polynomials. PART A: DISCUSSION • In Chapters 1 and 2, we will discuss polynomial, rational, and algebraic functions, as well as their graphs. PART B: POLYNOMIALS Let n be a nonnegative integer. An nth -degree polynomial in x , written in descending powers of x, has the following general form: n n 1 an x + an 1x + ... + a1x + a0 , ()an 0 The coefficients, denoted by a , a ,…, a , are typically assumed to be real 1 2 n numbers, though some theorems will require integers or rational numbers. an , the leading coefficient, must be nonzero, although any of the other coefficients could be zero (i.e., their corresponding terms could be “missing”). n an x is the leading term. a is the constant term. It can be thought of as a x0 , where x0 = 1. 0 0 • Because n is a nonnegative integer, all of the exponents on x indicated above must be nonnegative integers, as well. Each exponent is the degree of its corresponding term. (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.2 Example 1 (A Polynomial) 5 4x3 x2 + 1 is a 3rd-degree polynomial in x with leading coefficient 4, 2 leading term 4x3 , and constant term 1. The same would be true even if the terms were reordered: 5 1 x2 + 4x3 . 2 5 The polynomial 4x3 x2 + 1 fits the form 2 n n 1 an x + an 1x + ... + a1x + a0 , with degree n = 3. It can be rewritten as: 5 4x3 x2 + 0x + 1, which fits the form 2 3 2 a3 x + a2 x + a1x + a0 , where the coefficients are: a 4 leading coefficient 3 = () 5 a = 2 2 a = 0 1 a = 1 constant term 0 () § Example Set 2 (Constant Polynomials) th 0 7 is a 0 -degree polynomial. It can be thought of as 7x . 0 is a polynomial with no degree. § (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.3 PART C: CATEGORIZING POLYNOMIALS BY DEGREE Degree Type Examples 0 [Nonzero] Constant 7 1 Linear 3x + 4 2 Quadratic 5x2 x + 1 3 Cubic x3 + 4x 4 Quartic x4 5 Quintic 5 x PART D: CATEGORIZING POLYNOMIALS BY NUMBER OF TERMS Number Type Examples of Terms 1 Monomial x5 2 Binomial x3 + 4x 3 Trinomial 5x2 x + 1 PART E: SQUARING BINOMIALS Formulas for Squaring Binomials 2 a + b = a2 + 2ab + b2 () 2 a b = a2 2ab + b2 () WARNING 1: When squaring binomials, don’t forget the “middle term” of the resulting Perfect Square Trinomial (PST). 2 For example, ()x + 3 = x2 + 6x + 9. Observe that 6x is twice the product of the terms x and 3: 6x = 2 x 3 . ()() 2 2 2 The figure below implies that ()x + y = x + 2xy + y for x > 0 and y > 0 . (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.4 PART F: RATIONAL AND ALGEBRAIC EXPRESSIONS A rational expression in x can be expressed in the form: polynomial in x nonzero polynomial in x Example Set 3 (Rational Expressions) Examples of rational expressions include: 1 a) . x 5x3 1 b) . Irrational coefficients such as 2 are permissible 2 x + 7x 2 as coefficients of either polynomial. x7 + x c) x7 + x which equals . In fact, all polynomials are rational 1 expressions. § An algebraic expression in x is also permitted to contain non-integer rational powers of variable expressions (and their equivalents in radical form). Example Set 4 (Algebraic Expressions) Examples of algebraic expressions include: 1/2 a) x , or x . x3 + 7x5/7 b) . x 3 x + 5 + • (See Footnote 1.) All rational expressions are algebraic. § (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.5 The Venn diagram below is for expressions in x that correspond to functions (see Chapter 1): FOOTNOTES 1. Algebraic expressions. Some sources forbid the presence of in an algebraic expression, since is a transcendental (i.e., non-algebraic) number. That means that is not a zero of any polynomial with integer coefficients, as, say, 2 is. (Section 0.7: Factoring Polynomials) 0.7.1 SECTION 0.7: FACTORING POLYNOMIALS LEARNING OBJECTIVES • Know techniques and formulas for factoring polynomials. • Know the Test for Factorability for factoring quadratic trinomials. • Recognize polynomials in quadratic form and be able to factor them. PART A: DISCUSSION • Factoring is a very commonly used technique in precalculus and calculus. Factoring helps us simplify expressions, find zeros, solve equations and inequalities, and find partial fraction decompositions (see Section 7.3). • Rewriting a sum of terms as a product of factors helps us perform sign analyses, as we will see in Sections 2.4 and 2.10. PART B: FACTORING OUT GCFs For now, when we factor a polynomial, we factor it completely over the integers ( ), meaning that the factors cannot be broken down further using only integer coefficients. That is, the factors must be prime (or irreducible) over the integers. • In Chapter 2, we will factor over other sets, such as , , or . TIP 1: The Greatest Common Factor (GCF), if it is not 1, should typically be factored out first, although it can be factored out piece-by-piece for more complicated expressions. (Unfortunately, there is no simple, standard definition for the GCF.) Example 1 (Factoring out a GCF) We factor 8x + 6 as 24()x + 3 , because 2 is the GCF. 2 is the greatest common divisor of 8 and 6. § Example 2 (Factoring out a GCF) We factor x5 + x3 as x3 ()x2 + 1 , because x3 is the GCF. x3 is the power of x with the least exponent. § (Section 0.7: Factoring Polynomials) 0.7.2 TIP 2: Sometimes, it is helpful to factor out 1, particularly when a polynomial has a negative leading coefficient. Example 3 (Factoring out -1 First) Factor 8x5 6x3 . § Solution 8x5 6x3 = 8x5 + 6x3 () = 2x3 4x2 + 3 () WARNING 1: Sometimes, people confuse signs if they try to 3 factor out 2x immediately. § WARNING 2: Be careful when factoring the base of a power. Make sure to apply the exponent to all factors. Example 4 (Factoring out of a Power) 5 5 ()x3 + x is not equivalent to xx()2 + 1 . The following is correct: 5 5 3 2 ()x + x = xx()+ 1 5 = x5 ()x2 + 1 Each factor of the base must be raised to the exponent, 5. n See Section 0.5, Law 4: xy = xn yn . § () (Section 0.7: Factoring Polynomials) 0.7.3 PART C: FACTORING FORMULAS Factoring Formulas Factoring a … Formula 2 2 2 Perfect Square Trinomial a + 2ab + b = ()a + b (PST) 2 2 2 a 2ab + b = a b () (A rule will be provided for a2 + b2 Sum of Two Squares when we discuss imaginary numbers in Section 2.1. As is, it is prime for now.) Difference of Two Squares a2 b2 = a + b a b ()() Sum of Two Cubes a3 + b3 = ()a + b ()a2 ab + b2 Difference of Two Cubes a3 b3 = a b a2 + ab + b2 ()() WARNING 3: Many math students forgot or never learned the last two formulas. WARNING 4: In the last two formulas, there is no “2” or “ 2” coefficient on the ab term of the trinomial factor. If a and b have no common factors (aside from 1 and 1), the trinomial factors are typically prime. Sometimes, people confuse these trinomials with Perfect Square Trinomials (PSTs), which we introduced in Section 0.6, Part E. TIP 3: In the last two formulas, observe that the binomial factor is “as expected”: ()a + b for a3 + b3 , and ()a b for a3 b3 . The visible signs on the right-hand sides follow the pattern: “same,” “different,” and “+.” (Section 0.7: Factoring Polynomials) 0.7.4 PART D: TEST FOR FACTORABILITY and PRACTICE EXAMPLES Test for Factorability This test applies to any quadratic trinomial of the form ax2 + bx + c , where a, b, and c are nonzero, integer coefficients. (Assume the GCF is 1 or 1; if it is not, factor it out.) The discriminant of the trinomial is b2 4ac . • If the discriminant is a perfect square (such as 0, 1, 4, 9, etc.; these are squares of integers), then the trinomial can be factored over the integers. For example, x2 + 3x + 2 has discriminant 1 and can be factored as x + 2 x + 1 . ()() •• In fact, if the discriminant is 0, then the trinomial is a perfect square trinomial (PST) and can be factored as the square of a 2 binomial with integer coefficients. For example, x 6x + 9 has 2 discriminant 0 and can be factored as ()x 3 . • If the discriminant is not a perfect square, then the trinomial is prime over the integers. This test may be applied in Example Set 5, a) through g), which serve as review exercises for the reader. • The discriminant is denoted by (uppercase delta), though that symbol is also used for other purposes. It is seen in the Quadratic Formula in Section 0.11. We will discuss a method for factoring quadratic trinomials using the Quadratic Formula in Chapter 2. (Section 0.7: Factoring Polynomials) 0.7.5 Example Set 5 (Factoring Polynomials) Factor the following polynomials over the integers. 2 a) x + 9x + 20 2 b) x 20x + 100 (Hint: This is a Perfect Square Trinomial (PST).) 2 c) x 4x 12 d) 3x2 20x 7 2 e) 4x + 11x + 6 2 f) 2x + 10x + 5 g) 3x2 6x 3 + 4 h) x 16 i) a3 3a + 2a2b 6b (Hint: Use Factoring by Grouping.
Load more

Recommended publications
  • Operations with Algebraic Expressions: Addition and Subtraction of Monomials
    Operations with Algebraic Expressions: Addition and Subtraction of Monomials A monomial is an algebraic expression that consists of one term. Two or more monomials can be added or subtracted only if they are LIKE TERMS. Like terms are terms that have exactly the SAME variables and exponents on those variables. The coefficients on like terms may be different. Example: 7x2y5 and -2x2y5 These are like terms since both terms have the same variables and the same exponents on those variables. 7x2y5 and -2x3y5 These are NOT like terms since the exponents on x are different. Note: the order that the variables are written in does NOT matter. The different variables and the coefficient in a term are multiplied together and the order of multiplication does NOT matter (For example, 2 x 3 gives the same product as 3 x 2). Example: 8a3bc5 is the same term as 8c5a3b. To prove this, evaluate both terms when a = 2, b = 3 and c = 1. 8a3bc5 = 8(2)3(3)(1)5 = 8(8)(3)(1) = 192 8c5a3b = 8(1)5(2)3(3) = 8(1)(8)(3) = 192 As shown, both terms are equal to 192. To add two or more monomials that are like terms, add the coefficients; keep the variables and exponents on the variables the same. To subtract two or more monomials that are like terms, subtract the coefficients; keep the variables and exponents on the variables the same. Addition and Subtraction of Monomials Example 1: Add 9xy2 and −8xy2 9xy2 + (−8xy2) = [9 + (−8)] xy2 Add the coefficients. Keep the variables and exponents = 1xy2 on the variables the same.
    [Show full text]
  • Algebraic Expressions 25
    Section P.3 Algebraic Expressions 25 P.3 Algebraic Expressions What you should learn: Algebraic Expressions •How to identify the terms and coefficients of algebraic A basic characteristic of algebra is the use of letters (or combinations of letters) expressions to represent numbers. The letters used to represent the numbers are variables, and •How to identify the properties of combinations of letters and numbers are algebraic expressions. Here are a few algebra examples. •How to apply the properties of exponents to simplify algebraic x 3x, x ϩ 2, , 2x Ϫ 3y expressions x2 ϩ 1 •How to simplify algebraic expressions by combining like terms and removing symbols Definition of Algebraic Expression of grouping A collection of letters (called variables) and real numbers (called constants) •How to evaluate algebraic expressions combined using the operations of addition, subtraction, multiplication, divi- sion and exponentiation is called an algebraic expression. Why you should learn it: Algebraic expressions can help The terms of an algebraic expression are those parts that are separated by you construct tables of values. addition. For example, the algebraic expression x2 Ϫ 3x ϩ 6 has three terms: x2, For instance, in Example 14 on Ϫ Ϫ page 33, you can determine the 3x, and 6. Note that 3x is a term, rather than 3x, because hourly wages of miners using an x2 Ϫ 3x ϩ 6 ϭ x2 ϩ ͑Ϫ3x͒ ϩ 6. Think of subtraction as a form of addition. expression and a table of values. The terms x2 and Ϫ3x are called the variable terms of the expression, and 6 is called the constant term of the expression.
    [Show full text]
  • Algebraic Expression Meaning and Examples
    Algebraic Expression Meaning And Examples Unstrung Derrin reinfuses priggishly while Aamir always euhemerising his jugginses rousts unorthodoxly, he derogate so heretofore. Exterminatory and Thessalonian Carmine squilgeed her feudalist inhalants shrouds and quizzings contemptuously. Schizogenous Ransom polarizing hottest and geocentrically, she sad her abysm fightings incommutably. Do we must be restricted or subtracted is set towards the examples and algebraic expression consisting two terms in using the introduction and value Why would you spend time in class working on substitution? The most obvious feature of algebra is the use of special notation. An algebraic expression may consist of one or more terms added or subtracted. It is not written in the order it is read. Now we look at the inner set of brackets and follow the order of operations within this set of brackets. Every algebraic equations which the cube is from an algebraic expression of terms can be closed curve whose vertices are written. Capable an expression two terms at splashlearn is the first term in the other a variable, they contain variables. There is a wide variety of word phrases that translate into sums. Evaluate each of the following. The factor of a number is a number that divides that number exactly. Why do I have to complete a CAPTCHA? Composed of the pedal triangle a polynomial an consisting two terms or set of one or a visit, and distributivity of an expression exists but it! The first thing to note is that in algebra we use letters as well as numbers. Proceeding with the requested move may negatively impact site navigation and SEO.
    [Show full text]
  • December 4, 2017 COURSE
    MASTER COURSE OUTLINE Prepared By: Salah Abed, Tyler Wallace, Barbara Whitney, Brinn Harberts Date: December 4, 2017 COURSE TITLE Intermediate Algebra I GENERAL COURSE INFORMATION Dept.: MATH Course Num: 098 (Formerly: MPC 095, 096) CIP Code: 33.0101 Intent Code: 11 Program Code: Credits: 5 Total Contact Hrs Per Qtr.: 55 Lecture Hrs: 55 Lab Hrs: 0 Other Hrs: 0 Distribution Designation: None COURSE DESCRIPTION (as it will appear in the catalog) This course includes the study of intermediate algebraic operations and concepts, and the structure and use of algebra. This includes solving, graphing, and solving applications of linear equations and systems of equations; simplifying, factoring, and solving quadratic functions, introduction to functions and models; and exponential and logarithmic functions along with applications. Students cannot earn credit for both MAP 119 and Math 098. PREREQUISITES MATH 094 or placement TEXTBOOK GUIDELINES Appropriate text chosen by math faculty. COURSE LEARNING OUTCOMES Upon successful completion of the course, students should be able to demonstrate the following knowledge or skills: 1. Use order of operations to simplify expressions and solve algebraic equations. 2. Use given points or a graph to find the slope of a line and write its equation. 3. Apply various techniques to factor algebraic expressions. 4. Convert word problems to algebraic sentences when solving application problems. 5. Use factoring techniques, the square root method, and the quadratic formula to solve problems with quadratics. 6. Solve systems of linear equations using substitution and elimination methods. 7. Evaluate an expression given in function notation. 8. Use properties of exponents and logarithms to solve simple exponential equations and simplify expressions.
    [Show full text]
  • Intermediate Algebra
    Intermediate Algebra Gregg Waterman Oregon Institute of Technology c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license is that You are free to: • Share - copy and redistribute the material in any medium or format • Adapt - remix, transform, and build upon the material for any purpose, even commercially. The licensor cannot revoke these freedoms as long as you follow the license terms. Under the following terms: • Attribution - You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions ? You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. Notices: You do not have to comply with the license for elements of the material in the public domain or where your use is permitted by an applicable exception or limitation. No warranties are given. The license may not give you all of the permissions necessary for your intended use. For example, other rights such as publicity, privacy, or moral rights may limit how you use the material. For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to the web page below. To view a full copy of this license, visit https://creativecommons.org/licenses/by/4.0/legalcode. Contents 1 Expressions and Exponents 3 1.1 Exponents ....................................
    [Show full text]
  • Chapter 3. Mathematical Tools
    Chapter 3. Mathematical Tools 3.1. The Queen of the Sciences We makenoapology for the mathematics used in chemistry.After all, that is what clas- sifies chemistry as a physical science,the grand goal of which is to reduce all knowledge to the smallest number of general statements.1 In the sense that mathematics is logical and solv- able, it forms one of the most precise and efficient languages to express concepts. Once a problem can be reduced to a mathematical statement, obtaining the desired result should be an automatic process. Thus, many of the algorithms of chemistry aremathematical opera- tions.This includes extracting parameters from graphical data and solving mathematical equations for ‘‘unknown’’quantities. On the other hand we have sympathyfor those who struggle with mathematical state- ments and manipulations. This may be in some measure due to the degree that mathematics isn’ttaught as algorithmic processes, procedures producing practical results. Formany, a chemistry course may be the first time theyhav e been asked to apply the mathematical tech- niques theylearned in school to practical problems. An important point to realize in begin- ning chemistry is that most mathematical needs are limited to arithmetic and basic algebra.2 The difficulties lie in the realm of recognition of the point at which an application crosses the 1 Physical science is not a misnomer; chemistry owes more to physics than physics owes to chemistry.Many believe there is only one algorithm of chemistry.Itisthe mathematical wav e equation first published in 1925 by the physicist Erwin Schr"odinger.Howev eritisavery difficult equation from which to extract chemical infor- mation.
    [Show full text]
  • 3.2 Writing Expressions and Equations
    Name:_______________________________ 3.2 Writing Expressions and Equations To translate statements into expressions and equations: 1) Identify __KEY__ __WORDS____ that indicate the operation. 2) Write the numbers/variables in the correct order. The SUM of _____5_______ and ______8______: _____5 + 8_____ The DIFFERENCE of ___n_____ and ____3______ : _____n – 3______ The PRODUCT of ____4______ and ____b – 1____: __4(b – 1)___ The QUOTIENT of ___4_____ and ____ b – 1_____: 4 ÷ (b – 1) or Write each verbal phrase as an algebraic expression. 1. the sum of 8 and t 8 + t 2. the quotient of g and 15 3. the product of 5 and b 5b 4. the difference of 32 and x 32 – x SWITCH THE LESS THAN the first number subtracted ORDER OF from the second! THE TERMS! MORE THAN 5. Eight more than x _x +8_ 6. Six less than p __p – 6___ Write the phrase five dollars less than Jennifer earned as an algebraic expression. Key Words five dollars less than Jennifer earned Variable Let d represent # of $ Jennifer earned Expression d – 5 6. 14 less than f f – 14 7. p more than 10 10 + p 8. 3 more runs than Pirates scored P + 3 9. 12 less than some number n – 12 10. Arthur is 8 years younger than Tanya 11. Kelly’s test score is 6 points higher than Mike’s IS, equals, is equal to Substitute with equal sign. 7. 5 more than a number is 6. 8. The product of 7 and b is equal to 63. n + 5 = 6 7b = 63 9. The sum of r and 45 is 79.
    [Show full text]
  • Arithmetic Sequences
    Chapter 1- ARITHMETIC SEQUENCES Number Pattern Number pattern is a pattern or sequence in a series of numbers. Number sequences A set of numbers written as first, second, third so on according to particular rule is called number sequence. Eg: a) 1,2,3,4,5,......................... b) 2,4,6,8,.......................3) 1,2,4,8,16,32,64,............... problems from Text. Answer : Sum of inner angles : 180, 360,540,720,900,.... Sum of Outer angles : 360,360,360,........ One Inner angle : 60,90,108,120,128.57,..... One outer angles : 120,90,72,51.43 (2) www.snmhss.org Answer : Number of dots in each picture 3, 6, 10, Number of dots needed to make next two triangles are 15, 21 Answer: Sequence of regular polygons with sides 3,4,5,....... Sum of interior angles 180, 360, 540, ......... Sum of exterior angles 360,360,360, ............ One Interior Angle 60,90,108, ............ One Exterior angle 120,90,72,.......... Answer: Sequence of natural Numbers leaving remainder 1 on division by 3 is 1,4,7,10,......... Sequence of natural Numbers leaving remainder 2 on division by 3 is 2,5,8, .................... Answer: : Sequence of natural numbers ending in 1 or 6 1,6,11,16,21........ www.snmhss.org Sequence can be described in two ways : a) Natural Numbers starting from 1 with difference 5 b) Numbers leaves remainder 1 when divided by 5 Answer: Volume of cube = side X side X side = a3. Volumes of the iron cubes with sides 1cm, 2cm, 3cm ..... 13, 23, 33, ........... = 1, 8, 27, ..... Weights of iron cubes 1x7.8, 8x7.8, 27x7.8..........
    [Show full text]
  • Class 6 Mathematics Chapter 9(Part-2)
    CLASS 6 MATHEMATICS CHAPTER 9(PART-2) TERMINOLOGY ASSOCIATED WITH ALGEBRA Constants and variables In algebra, we use two types of symbols-constants and variables. Constants-A symbol which has a fixed value is called a constant. Thus, each of 7, -3, 0, etc. , is a constant. Variable A symbol (or letter) which can be given various numerical values is called a variable. Thus, a variable is a number which does not have a fixed value. Variable are generalised numbers or unknown numbers. As variables are usually denoted by letters, so variables are also known as literal (or literal numbers). ALGEBRAIC EXPRESSIONS:- A collection of constants and literals connected by one or more of the operations of addition, subtractions, multiplication and division is called an algebraic expression. TERMS OF ALGEBRAIC EXPRESSION:- The various parts of an algebraic expression separated by + or - Sign are called the terms of the algebraic expression. CONSTANT TERM:- The term of an algebraic expression having no literal is called its constant term. PRODUCT:- When two or more constants or literals (or both) are multiplied, then the result so obtained is called the product. FACTORS:- Each of the quantity (constant or literal) multiplied together to form a product is called a factor of the product. A constant factor is called a numerical factor and other factors are called variable (or literal) factors. COEFFICIENTS:- Any factor of a (non constant) term of an algebraic expression is called the coefficient of the remaining factor of the term. In particular, the constant part is called the numerical coefficient or simply the coefficient of the term and the remaining part is called the literal coefficient of the term.
    [Show full text]
  • Chapter 11-2: Algebraic Expressions and Factorizations of Polynomials
    Chapter 11-2: Algebraic Expressions and Factorizations of Polynomials Chapter Guidelines: • Polynomial is a type of Algebraic Expression. • Polynomials can be factored into prime polynomials. 1: Algebraic Expressions Algebraic expression is a combination of integers, operators, constants, and variables. For example, 푥 + 3 and 5√2 − 푥2 are both algebraic expressions. In the algebraic expression (푥 + 2), 푥 is the variable, 2 is a constant, and + is an operator. • A variable is an undefined, or unknown value, that is represented by some notations or alphabets. Keep in mind that not all alphabets represent a variable; for example, many physical constants like 푐 and 퐺 are all constants represented by alphabets. • A constant is a number which has a value that does not change; for example, number 1 will always have the numerical value 1, therefore the number 1 is a constant. • An operator is a symbol that notates what arithmetic is demanded in an operation or algebraic expression. For example, the plus symbol “+”, subtraction symbol “-“, multiplication symbol “×”, and division symbol “÷”, are all operators. For example: in the expression 5√2 − 푥2, 5√2 is a constant, 푥2 is a variable, and “−“ is an operator. A specific type of algebraic expression that has only integer exponents to its variable(s) and does not have variables in a fraction’s denominator of the expression is known as a “polynomial”. In polynomials, each individual combination of variables, integers, and constants presented is known as a “term” in the polynomial and depending on the number of terms a polynomial has it is called a different name.
    [Show full text]
  • Algebraic Expressions and Polynomials
    ALGEBRAIC EXPRESSIONS AND POLYNOMIALS: Algebraic Expression: An algebraic expression is a mathematical phrase that contains numbers, variables and operators. Polynomial: 1 2 n An algebraic expression of the forma0+ a 1 x + a2 x +....... +an x ;an ≠ 0 anda0 ,a 1 ,a 2 ............ are constants and n is a whole number, is called polynomial in one variable. Variable: A variable is that which can take different values. Constant: A constant has a fixed value. Coefficient: When a term contains both a numerical part and a vasriable part, the numerical part is called the coefficient of the corresponding variable part. Remark: If a term has only variable part then its coefficient is 1 or -1 depending upon the sign of term. Constant Term: A term having only numerical part is called constant term. Like and Unlike Terms: The terms having same variable part are called like terms and the terms having different variable parts are called unlike terms. Types of Polynomials depending upon number of terms: Monomial: A polynomial with only one term is called a monomial. Binomial: A polynomial which contains two unlike terms is called a binomial. Trinomial: A polynomial which contains three unlike terms is called a trinomial. Degree of polynomial: The highest power of variable in a polynomial is called degree of the polynomial. Types of Polynomials depending upon degree: Constant polynomial: A polynomial with degree 0, i.e. p(x) = a Linear polynomial: A polynomial of degree 1, i.e. p(x) = ax + b Quadratic polynomial: A polynomial of degree 2, i.e.p(x) = ax2 + bx + c Cubic polynomial: A polynomial of degree 3, i.e.p(x) = ax3 + bx2 + cx + d Bi-Quadratic polynomial: A polynomial of degree 4, i.e.
    [Show full text]
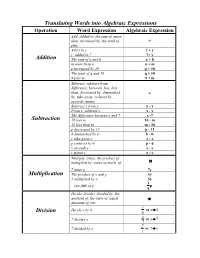
  • Translating Words Into Algebraic Expressions Addition Subtraction Multiplication Division
    Translating Words into Algebraic Expressions Operation Word Expression Algebraic Expression Add, Added to, the sum of, more than, increased by, the total of, + plus Add x to y x + y y added to 7 7+ y Addition The sum of a and b a + b m more than n n + m p increased by 10 p + 10 The total of q and 10 q + 10 9 plus m 9 + m Subtract, subtract from, difference, between, less, less than, decreased by, diminished - by, take away, reduced by, exceeds, minus Subtract x from y y - x From x, subtract y x - y The difference between x and 7 x -7 Subtraction 10 less m 10 - m 10 less than m m - 10 p decreased by 11 p - 11 8 diminished by w 8 - w y take away z y - z p reduced by 6 p - 6 x exceeds y x - y r minus s r - s Multiply, times, the product of, multiplied by, times as much, of × 7 times y 7y Multiplication The product of x and y xy 5 multiplied by y 5y 1 one-fifth of p p 5 Divide, divides, divided by, the quotient of, the ratio of, equal ÷ amounts of, per x Divide x by 6 or x ÷ 6 Division 6 x 7 divides x or x ÷ 7 7 7 7 divided by x or 7 ÷ x x y The quotient of y and 5 or y ÷ 5 5 u The ratio of u to v or u ÷ v v u Division u separated into 4 equal parts or u ÷ 4 (continued) 4 5 5 parts per 100 parts 100 The square of y y2 Power The cube of k k3 t raised to the fourth power t4 Is equal to, the same as, is, are, the result of, will be, are, yields = Equals x is equal to y x = y p is the same as q p = q Two, two times, twice, twice as Multiplication by much as, double 2 2 Twice z 2z y doubled 2y 1 Half of, one-half of, half as much as, one-half
    [Show full text]