Surface Parametrization of Nonsimply Connected Planar B\'Ezier Regions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Graphics for Latex Users (Arstexnica, Numero 28, 2019)
Graphics for LATEX users Agostino De Marco Abstract able, coherent, and visually satisfying whole that works invisibly, without the awareness of the reader. This article presents the most important ways to Typographers and graphic designers claim that an produce technical illustrations, diagrams and plots, A even distribution of typeset material and graphics, which are relevant to LTEX users. Graphics is a with a minimum of distractions and anomalies, is huge subject per se, therefore this is by no means aimed at producing clarity and transparency. This an exhaustive tutorial. And it should not be so is even more true for scientific or technical texts, since there are usually different ways to obtain where also precision and consistency are of the an equally satisfying visual result for any given utmost importance. graphic design. The purpose is to stimulate read- Authors of technical texts are required to be ers’ creativity and point them to the right direc- aware and adhere to all the typographical conven- tion. The article emphasizes the role of tikz for A tions on symbols. The most important rule in all programmed graphics and of inkscape as a LTEX- circumstances is consistency. This means that a aware visual tool. A final part on scientific plots given symbol is supposed to always be presented in presents the package pgfplots. the same way, whether it appears in the text body, a title, a figure, a table, or a formula. A number Sommario of fairly distinct subjects exist in the matter of typographical conventions where proven typeset- Questo articolo presenta gli strumenti più impor- ting rules have been established. -
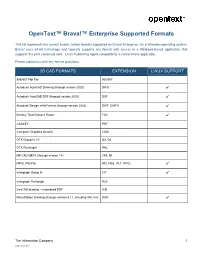
Opentext Brava Enterprise Supported Formats
OpenText™ Brava!™ Enterprise Supported Formats This list represents the current known, tested formats supported by Brava! Enterprise. On a Windows operating system, Brava! uses 64-bit technology and typically supports any format with access to a Windows-based application that supports the print canonical verb. Linux Publishing Agent compatibility is noted where applicable. Please contact us with any format questions. 2D CAD FORMATS EXTENSION LINUX SUPPORT 906/907 Plot File 906/907 Autodesk AutoCAD Drawing (through version 2020) DWG ✓ Autodesk AutoCAD DXF (through version 2020) DXF ✓ Autodesk Design Web Format (through version 2020) DWF, DWFX ✓ Bentley Tiled Group 4 Raster TG4 ✓ CADKEY PRT Computer Graphics Metafile CGM GTX Group III, IV G3, G4 GTX Runlength RNL HP CAD ME10 (through version 13) CMI, MI HPGL Plot File 000, HGL, PLT, HPGL ✓ Intergraph Group IV CIT ✓ Intergraph Runlength RLE IronCAD drawing – embedded PDF ICD MicroStation Drawing (through version 8.11, including XM, V8i) DGN ✓ The Information Company 1 2020-09 16 EP7 Brava! Enterprise Formats 3D CAD FORMATS 1 EXTENSION LINUX SUPPORT Adobe 3D PDF 7 PDF ✓ Autodesk AutoCAD Drawing DWG ✓ Autodesk Design Web Format DWF ✓ Autodesk Inventor (through version 2019) IPT, IAM ✓ Autodesk Revit 8 (2015 to 2020) RVT, RFA ✓ CATIA V4 MODEL, SESSION, DLV, EXP ✓ CATIA V5 CATPart, CATProduct, ✓ CATShape, CGR CATIA V6 3DXML ✓ HOOPS Streaming Format 2 HSF ✓ I-DEAS and NX I-DEAS 6 MF1, ARC, UNV, PKG ✓ Industry Foundation Classes (versions 2, 3, 4) IFC ✓ Initial Graphics Exchange Specification -
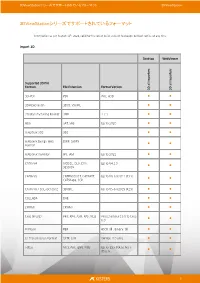
L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L
Information as per August 11th, 2021, valid for the latest build, subject to change without notice at any time Import 3D Desktop WebViewer s s r r e e t t r r o o p p m m i i l l Supported 3D File l l a a Formats File Extension Format Version D D 3 3 3D-PDF PDF PRC, U3D l l 3DViewStation 3DVS, VSXML l l 3D Manufacturing Format 3MF 1.2.3 l l ACIS SAT, SAB Up to 2020 l l Autodesk 3DS 3DS l l Autodesk Design Web DWF, DWFX l l Format Autodesk Inventor IPT, IAM Up to 2022 l l CATIA V4 MODEL, DLV, EXP, Up to V4.2.5 l l SESSION CATIA V5 CATPRODUCT, CATPART, Up to V5-6 R2021 (R31) l l CATShape, CGR CATIA V6 / 3DExperience 3DXML Up to V5-6 R2019 (R29) l l COLLADA DAE l l CPIXML CPIXML l l Creo (Pro/E) PRT, XPR, ASM, XAS, NEU Pro/Engineer 19.0 to Creo l l 8.0 Filmbox FBX ASCII: all ; Binary: all l l GL Transmission Format GLTF, GLB Version 2.0 only l l I-deas MF1, ARC, UNV, PKG Up to 13.x (NX 5), NX I- l l deas 6 Desktop WebViewer s s r r e e t t r r o o p p m m i i l l Supported 3D File l l a a Formats File Extension Format Version D D 3 3 IGES IGS, IGES 5.1, 5.2, 5.3 l l Industry Foundation IFC IFC 2x2, 2x3, 2x4 l l Classes JTOpen JT Up to 10.5 l l LIDAR Point Cloud Data E57 l l File1 MineCraft² NBT l l NX (Unigraphics) PRT UG v11.0 to v1980 l l Parasolid X_T, X_B Up to v33.1 l l PLMXML PLMXML l l PRC PRC l l Autodesk Revit RVT, RFA 2015 to 2021 l l Rhino3D 3DM 4 - 7 l l Solid Edge ASM, PAR, PWD, PSM V19 – 20, ST – ST10, 2021 l l SolidWorks SLDASM, SLDPRT From 97 up to 2021 l l STEP Exchange STP, STEP, STPZ AP 203 E1/E2, AP 214, AP l l 242 STEP/XML STPX, STPXZ l l Stereo Lithography STL l l Universal 3D U3D ECMA-363 (1-3. -

3Dviewstation VR-Edition
What Your YOU GET BENEFITS SAVE TIME AND MONEY 1 Speed up the process chain in your company with our 3DViewStation Desktop. ALL-IN-ONE SOLUTION 2 Analyze your models with more than 180 functions available: sectioning, measurement and much more. 3DViewStation EASY TO USE 3 Intuitive UI, easy to install - easy for everyone. Start Desktop working instantly. KISTERS 3DViewStation works with even the largest of assemblies, such as: vehicles, machines or buildings – up to millions of parts. MANY DATA FORMATS – PLUS MULTICAD View all your daily CAD models and documents – we 3DViewStation is a powerful 3D CAD viewer and universal 4 support more than 70 different file formats. viewer for engineers and designers, made for 3D viewing, 3D CAD analysis, 2D viewing, Office viewing, technical documentation and 3D publishing. If you are looking for an ULTRA FAST LOAD TIMES intuitive, easy-to-use application to load CAD data, measure, 5 Work with your files immediately - load millions of parts slice, and to compare components or assemblies quickly and in seconds instead of waiting for your models to load. easily – you’ve found it. We have done our best to ensure that your work with 3DViewStation is a real pleasure. LARGE MODEL VISUALIZATION 6 Work with massively large data (up to 10,000,000 objects) – due to the high-end VS rendering kernel. FOR EVERYONE 7 For all users and departments: from sales and engineering to manufacturing and project reviews. INTEGRATION AND AUTOMATION REUSE, EXPLORE & 8 Use our comprehensive API for any kind of automation and integration (PLM, ERP,…). VIEW YOUR CAD DATA If you would like more information or a demo license to test 3DViewStation Desktop on your own, please contact us at: - make the most Explore and analyze your CAD data. -

Long Term Archiving with 3D PDF
Long Term Archiving with 3D PDF 3D PDF Consortium • Jerry McFeeters – Executive Director • Phil Spreier – Technical Director BOEING is a trademark of Boeing Management Company Copyright © 2014 Boeing. All rights reserved. Copyright © 2014 Northrop Grumman Corporation. All rights reserved. GPDIS_2015.ppt | 1 3D PDF Consortium Global Product Data Interoperability Summit | 2015 A community dedicated to driving adoption of 3D PDF enabled solutions through: • Defining industry needs and priorities • Creating reference implementations and other resources • Providing input to the standards process • Raising awareness A worldwide, non-profit, member organization Open to all companies BOEING is a trademark of Boeing Management Company Copyright © 2015 Boeing. All rights reserved. Copyright © 2014 Northrop Grumman Corporation. All rights reserved. GPDIS_2015.ppt | 2 3D PDF Consortium - Members Global Product Data Interoperability Summit | 2015 BOEING is a trademark of Boeing Management Company Copyright © 2015 Boeing. All rights reserved. Copyright © 2014 Northrop Grumman Corporation. All rights reserved. GPDIS_2015.ppt | 3 3D PDF Consortium - Organization Global Product Data Interoperability Summit | 2015 Board of Directors • Governance, Recruiting Committees Executive • Mission, Vision, Strategic Direction Industry Technical Communications • Define industry needs • Project goals and • Events planning and priorities objectives • Publications • Develop process- • Project plans, • Solicit and propose based use cases participation, case studies • -

Rapidauthor/Rapidauthor for Teamcenter 13.1 Supported 3D CAD Import Formats
RapidAuthor/RapidAuthor for Teamcenter 13.1 Supported 3D CAD Import Formats RapidAuthor Version 13.1 There are two different versions of the software: RapidAuthor and RapidAuthor for Teamcenter. RapidAuthor for Teamcenter is integrated with Teamcenter and imports JT data; RapidAuthor imports data in various CAD formats listed below. If the users of RapidAuthor for Teamcenter would like to import various CAD data listed in the RapidAuthor section of this document, they need to install RapidDataConverter for Teamcenter in addition to RapidAuthor for Teamcenter. Format Version Extensions I-deas Up to 13.x (NX 5), MF1, ARC, UNV, PKG NX I-deas 6 JT Up to 10.3 JT Parasolid Up to 32.0 X_B, X_T, XMT, XMT_TXT NX - Unigraphics Unigraphics V11.0 – PRT NX 12.0 and 1926 Solid Edge V19, V20, ST-ST10, ASM, PAR, PWD, PSM 2020 Format Version Extensions Creo Elements/Pro Pro/Engineer 19.0 ASM, NEU, PRT, XAS, XPR (earlier Pro/Engineer) to Creo 7.0 (c) 2011-2021 ParallelGraphics Ltd. All rights reserved. RapidAuthor/RapidAuthor for Teamcenter 13.1 Supported 3D CAD Import Formats Format Version Extensions Import of textures and texture coordinates Autodesk Inventor Up to 2021 IPT, IAM Supported AutoCAD Up to 2019 DWG, DXF Autodesk 3DS All versions 3ds Supported Autodesk DWF All versions DWF, DWFX Supported Autodesk FBX All binary versions, FBX Supported ASCII data 7100 – 7400 Format Version Extensions Import of textures and texture coordinates ACIS Up to 2020 SAT, SAB CATIA V4 Up to 4.2.5 MODEL, SESSION, DLV, EXP CATIA V5 Up to V5-6 R2020 CATDRAWING, (R29) CATPART, CATPRODUCT, CATSHAPE, CGR, 3DXML CATIA V6 / Up to V5-6 R2019 3DXML 3DExperience (R29) SolidWorks 97 – 2021 SLDASM, SLDPRT Supported (c) 2011-2021 ParallelGraphics Ltd. -

An Overview of 3D Data Content, File Formats and Viewers
Technical Report: isda08-002 Image Spatial Data Analysis Group National Center for Supercomputing Applications 1205 W Clark, Urbana, IL 61801 An Overview of 3D Data Content, File Formats and Viewers Kenton McHenry and Peter Bajcsy National Center for Supercomputing Applications University of Illinois at Urbana-Champaign, Urbana, IL {mchenry,pbajcsy}@ncsa.uiuc.edu October 31, 2008 Abstract This report presents an overview of 3D data content, 3D file formats and 3D viewers. It attempts to enumerate the past and current file formats used for storing 3D data and several software packages for viewing 3D data. The report also provides more specific details on a subset of file formats, as well as several pointers to existing 3D data sets. This overview serves as a foundation for understanding the information loss introduced by 3D file format conversions with many of the software packages designed for viewing and converting 3D data files. 1 Introduction 3D data represents information in several applications, such as medicine, structural engineering, the automobile industry, and architecture, the military, cultural heritage, and so on [6]. There is a gamut of problems related to 3D data acquisition, representation, storage, retrieval, comparison and rendering due to the lack of standard definitions of 3D data content, data structures in memory and file formats on disk, as well as rendering implementations. We performed an overview of 3D data content, file formats and viewers in order to build a foundation for understanding the information loss introduced by 3D file format conversions with many of the software packages designed for viewing and converting 3D files. -

Tetra4d Converter 2017 Users Guide – V2.0 1 Table of Contents
Tetra4D Converter Version 2017 User Guide Document version: V2.0. Tetra4D Converter 2017 Users Guide – V2.0 1 Table of Contents Chapter 1: Getting started .......................................................................................................................... 6 Help ......................................................................................................................................................... 6 Installation and activation .......................................................................................................................... 7 Installation of Acrobat XI Pro and Acrobat Pro DC ................................................................................. 7 System Requirements ............................................................................................................................. 7 Installation of Tetra4D Converter ........................................................................................................... 7 Running Tetra4D Converter ........................................................................................................................ 8 License activation.................................................................................................................................... 8 Chapter 2: Tetra4D Converter Overview .................................................................................................... 9 Tetra4D Converter for Acrobat XI Pro ................................................................................................... -

STANDARDS IMPACTING BUSINESS PERFORMANCE Virtual
Welcome to the 2020 GPDIS Virtual Sessions! Global Product Data Interoperability Summit | 2020 History and Focus of GPDIS • Global Product Data Interoperability Summit (GPDIS) was formed in 2009. It was the consolidation of two conferences (Data Exchange and SOA Deep Dives) addressing integration technologies along with the non- proprietary exchange of data • GPDIS functions as a communications hub for industry principals to foster knowledge through the exchange of ideas, solutions and methods. 2020 Theme: The Great Race of Digital Transformation How is your model based enterprise today? • Together we will explore digital transformation and what it will take us to FULLY achieve it. Using the Great Race as a metaphor, we will explore the building blocks of digital transformation and how interoperability will enable the digital transformation journey for industry. Mark your Calendars! GPDIS 2021 - September 13-17th Scottsdale, AZ CAMSC MBSE ET/IT 3D MBD DevOps PLM Roadmap PDES . GPDIS_2020.ppt | 1 Our Sponsors Global Product Data Interoperability Summit | 2020 . GPDIS_2020.ppt | 2 STANDARDS IMPACTING BUSINESS PERFORMANCE Virtual Improved efficiency and effectiveness through standards Sessions . GPDIS_2020.ppt | 3 Presenters Global Product Data Interoperability Summit | 2020 • Jack Harris, CEO/GM, PDES Inc. and Director, Advanced Manufacturing Technology and Engineering, Rockwell Collins (Retired) • Brandon Sapp, Lead for Boeing Strategy for Data Standards and Interoperability across the Enterprise, The Boeing Company • Phil Spreier, Executive Director, 3DPDF Consortium . GPDIS_2020.ppt | 4 Business Value Case Study – Rockwell Collins – Jack Harris Global Product Data Interoperability Summit | 2020 • In 2004 an industry consortium defined the Model Based Enterprise and its fit with the Digital Enterprise • BAE • Boeing • Honeywell • ITT • Lockheed Martin • Raytheon • Rockwell Collins • Sandia National Labs . -

Tetra4d Converter 2018 User Guide
Tetra4D Converter Version 2018 User Guide Document version: V3.0 Tetra4D Converter 2018 Users Guide – V3.0 1 Table of Contents Chapter 1: Getting started .......................................................................................................................... 6 Help ......................................................................................................................................................... 6 Installation and activation .......................................................................................................................... 7 Installation of Acrobat XI Pro and Acrobat Pro DC ................................................................................. 7 System Requirements ............................................................................................................................. 7 Installation of Tetra4D Converter ........................................................................................................... 7 Running Tetra4D Converter ........................................................................................................................ 8 License activation.................................................................................................................................... 8 Chapter 2: Tetra4D Converter Overview .................................................................................................... 9 Tetra4D Converter for Acrobat XI Pro ................................................................................................... -

TC 184/SC 4/JWG 16 for CAD Visualization
JWG16 - Formats for visualization and other derived forms of product data Joint ISO/TC 184/SC 4 - ISO/IEC JTC 1/SC 24 - ISO/TC 171/SC 2 WG https://isotc.iso.org/livelink/livelink?func=ll&objId=19599172&objA ction=browse&viewType=1 2018-11-09 Soonhung Han, [email protected] Christophe Mouton, [email protected] 1 Contents SC4 and JWG 16 Standard projects Liaison JWG 16 members Long term projects Chicago meeting Nov. 2018 2 ISO TC184/SC4 organization ISO/TC 184 Automation systems and integration 산업자동화 WG 6 SC 1 SC 5 SC 4 Oil & Gas Physical Interoperability, integration, Industrial Interoperability Device and architectures for Data 산업 데이터 enterprise systems and MIMOSA Control automation applications STEP-NC WG 2 JWG 8 WG 12 Part Manufacturing Common Libraries Management Resources Data (Mandate) (SMRL) WG 3 WG 11 WG 13 Oil & Gas Express, Data quality WG 15 Implement, JWG 16 Digital Conformance STEP Model Manufacturing 3 Visualization SMRL: STEP module and resource library Scope of industrial data Product Product parts Classification Libraries – ISO 13584 using ISO 22745 Data quality – ISO 8000 Oil and Gas – ISO 15926 Factory Interfaces Product characteristics from ISO 22745 ISO 15531 Product Definition data ISO 18629 ISO 18876 (STEP) – ISO 10303 ISO 18828 Visualisation – ISO 14306,17506 Industrial terminology using ISO 22745 9 Direct Working Groups 15 752 216 3 Participating members Published ISO Standard ISO Standards under de Joint Working Groups s velopment 3 Internal Committees 15 Observing members 5 JWG16 Established at Jeju 2017-11 6 JWG16 Work scope from SC4 resolution 2017-11 Develop and maintain format and interface standards for 3D visualization of product models, including visualization of different classes of derived information such as geometry, product structure and others. -
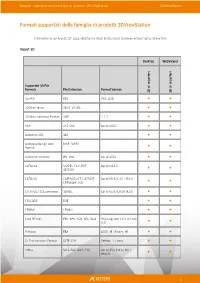
3Dviewstation File Formats
Formati supportati della famiglia di prodotti 3DViewStation 3DViewStation Formati supportati della famiglia di prodotti 3DViewStation Information as per August 11th, 2021, valid for the latest build, subject to change without notice at any time Import 3D Desktop WebViewer s s r r e e t t r r o o p p m m i i l l Supported 3D File l l a a Formats File Extension Format Version D D 3 3 3D-PDF PDF PRC, U3D l l 3DViewStation 3DVS, VSXML l l 3D Manufacturing Format 3MF 1.2.3 l l ACIS SAT, SAB Up to 2020 l l Autodesk 3DS 3DS l l Autodesk Design Web DWF, DWFX l l Format Autodesk Inventor IPT, IAM Up to 2022 l l CATIA V4 MODEL, DLV, EXP, Up to V4.2.5 l l SESSION CATIA V5 CATPRODUCT, CATPART, Up to V5-6 R2021 (R31) l l CATShape, CGR CATIA V6 / 3DExperience 3DXML Up to V5-6 R2019 (R29) l l COLLADA DAE l l CPIXML CPIXML l l Creo (Pro/E) PRT, XPR, ASM, XAS, NEU Pro/Engineer 19.0 to Creo l l 8.0 Filmbox FBX ASCII: all ; Binary: all l l GL Transmission Format GLTF, GLB Version 2.0 only l l I-deas MF1, ARC, UNV, PKG Up to 13.x (NX 5), NX I- l l deas 6 1 3DViewStation Formati supportati della famiglia di prodotti 3DViewStation Desktop WebViewer s s r r e e t t r r o o p p m m i i l l Supported 3D File l l a a Formats File Extension Format Version D D 3 3 IGES IGS, IGES 5.1, 5.2, 5.3 l l Industry Foundation IFC IFC 2x2, 2x3, 2x4 l l Classes JTOpen JT Up to 10.5 l l LIDAR Point Cloud Data E57 l l File1 MineCraft² NBT l l NX (Unigraphics) PRT UG v11.0 to v1980 l l Parasolid X_T, X_B Up to v33.1 l l PLMXML PLMXML l l PRC PRC l l Autodesk Revit RVT, RFA 2015 to 2021 l l Rhino3D 3DM 4 - 7 l l Solid Edge ASM, PAR, PWD, PSM V19 – 20, ST – ST10, 2021 l l SolidWorks SLDASM, SLDPRT From 97 up to 2021 l l STEP Exchange STP, STEP, STPZ AP 203 E1/E2, AP 214, AP l l 242 STEP/XML STPX, STPXZ l l Stereo Lithography STL l l Universal 3D U3D ECMA-363 (1-3.