DOCSLIB.ORG

Three-Dimensional Sound Intensity Measurements Using Microflown

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Three-Dimensional Sound Intensity Measurements Using Microflown THREE-DIMENSIONALSOUND INTENSITY MEASUREMENTS USING MICROFLO WN PARTICLE VELOCITY SENSORS Hans-Elias de Bree*, W.F. Druyvesteyn"", E. Berenschot*, M. Elwenspoek" * Micromechanical Transducers Group **LaboratorySignals & System Network theory University of Twente, P.O. Box 217,7500 AE Enschede, The Netherlands ABSTRACT This paper reports on a novel method to measure three-dimensional sound intensity and the fabrication of a miniature three-dimensional sound intensity probe. Verifying measurements where performed with three separate micro-machined particle velocity probes and one pressure microphone. A three-dimensional sound intensity probe has been realised based on a three- dimensional micro-machined particle velocity microphone, a 3D Microflown, and a miniature pressure microphone. INTRODUCTION A few years ago I had a discussion with the measurements. It consists of two very closely sales representative of a leading sound & spaced (40pm apart) heated platinum resistive vibration company. He claimed that the one temperature sensors. The temperature that was able to make a broadband sound difference of both sensors is linearly dependent intensity probe smaller than a sugar cube on the particle velocity. In combination with a should become a .wealthy person. Well, still pressure microphone a Microflown can form a poor but proud we present the miniature three- sound intensity probe, a so called p-U method, dimensional sound intensity probe. see Fig. 2 [3]. Sound intensity is a vector quantity, defined A one dimensional sound intensity probe as the time averaged product of the sound can be extended to a three dimensional probe pressure (a scalar quantity, p) and the by using three p-p probes (six microphones) or corresponding particle velocity (a vector one microphone and three Microflowns (p-u3). quantity, U) at the same position. The The realisation of a three-dimensional p-p measurement permits the determination of probe however is not very realistic. The prize radiated sound power without requiring special of such probe will be over 30,000 USD and the acoustic environments such as reverberation frequency range is limited even more than the and anechoic chambers. The measurement 1D p-p probe. technique is alsa used for sound source A broad band three-dimensional sound localisation. intensity probe however will offer many Since historically no particle velocity probes advantages. The magnitude and direction of the were available, the traditional way to measure acoustic energy flow can be measured directly, sound intensity was to use two closely spaced this will improve the effectiveness of the and phase matched pressure microphones. The measurement. The 3D measurement allows particle velocity is calculated by the difference measuring non-stationary sound fields as for of the signals from both the pressure example the noise of moving objects like microphones and the (average) sound pressure aeroplanes. is found from the sum of both. This method is Using of Microflown technology, a three- called the p-p method, see Fig. 1 [l]. dimensional sound intensity probe become Two major disadvantages of the p-p probe feasible. are its high prize and the fact that performing Preliminary measurements with three broad band measurements is time-consuming. separate (half-inch packaged) Microflowns and Furthermore the bandwidth of the probe is a half-inch pressure probe showed promising limited and the probe is fragile. results. Nowadays the Microflown [2] can perform Now a fully integrated three-dimensional the particle velocity measurement directly and Microflown has been realised. This will be a sound intensity measurement becomes another step in the direction of realisation of a possible without the mentioned disadvantages. rugged broad band three-dimensional sound A Microflown can be considered as a mass intensity probe. flow sensor that has been optimised for sound 0-7803-5194-0/99/$10.00 01999 IEEE 124 SOUND INTENSITY By measuring the pressure at two points at a close distance dr, the pressure gradient is Sound intensity is a vector quantity that approximated. describes the amount and direction of net flow of acoustic energy at a given position. It is defined as the time averaged product of the sound pressure (a scalar quantity, p) and the corresponding particle velocity (a vector This approximation is valid as long as the quantity, at the same position. separation, dr, is small compared to the U) wavelength. 1 I = - Ip(t)* u(t)dt BANDWIDTH(P-P) T The proper determination of the particle The electrical analogy is well known: velocity is frequency limited. The upper power=voltage x current. frequency is limited due to the fact that the Two methods to measure: the sound intensity estimation (dp/d-=(pa-pb)/dr)no longer holds. will be explained briefly: the p-p probe and the The lower frequency limit is caused by the p-U probe. For simplicity first the two methods phase mismatch of the two microphones and will be compared in their one directional electronics. realisation. The pros and cons will be extended In practice this means that the lowest later to the three dimensional versions. frequency that can be measured is best case (anechoic conditions) 20Hz and worst case THEP-P PIROBE 3 50Hz (reverberation, phase mismatch=0.3"). The smallest size of the microphone separation A p-p probe consists of two, closely spaced, equals the microphone diameter and bounds the matched pressure microphones [ 11. highest frequency that can be measured (approximately 1OkHz). SPACERS(P-P) To measure the complete bandwidth with a p-p probe three spacers and two types of microphones are used. Two half inch microphones and a spacer of 50" are used for the lower frequencies (20-350Hz to 1250Hz) the 12" spacer is used for the medium frequencies (250-1250 to 5kHz). Two Fig. 1: ID p-p B&K sound intensity probe (The quarter inch microphones and a spacer of 6mm microphones are a half inch in diameter). are used to measure in the higher frequencies The particle velocity is calculated by the (250-2000 to 1OkHz). The p-p probe has to be subtraction of the signals from both pressure disassembled and re-calibrated when changing microphones, The method is based upon spacers or microphones. This makes the broad Newton's second law, the equation of motion: band sound intensity measurement time consuming furthermore the use of these spacers will make the realisation of the probe fragile. NEARFIELDMEASUREMENTS (P-P) Where p is the density of the medium, ur is When a p-p probe is positioned in the the particle velocity in one direction r, and p nearfield of a sound source, the sound intensity the instantaneous pressure. Since the pressure is not constant from one pressure probe to the gradient is proportional to the particle other. This will lead to an overestimation. This acceleration, the particle velocity can be effect is present when the probe is placed obtained by integrating the pressure gradient in closer to the source than at least two times the respect to time. separation (of the microphones) and can be a problem at low frequencies. U, =-- I+j-dt Pa 125 THEP-U PROBE SIGNAL TO NOISE RATIO (P-P) Historically there has been a lack of particle An example of a high quality matched pair velocity probes. Nowadays the Microflown [2] is the Briiel & KjEr sound intensity can perform the particle velocity measurement microphone pair B&K 4181 [5]. One of the % directly and a p-U probe can be realised [3]. inch matched microphones has a selfnoise of The probe consists of a pressure microphone 20dB(A) and a sensitivity of 11.2 mV/Pa (at and a particle velocity microphone. 1kHz) . It will be convenient to express noise values in voltages and in one Hertz bandwidth. The noise is expressed in VIdHz. The latter corresponds to: U,,,,, =3 1.6nV/dHz at 1 kHz [51. ( Usrgna[=l1.2mV at 1 Pa (=94dB SPL) pressure at 1 kHz). The microphones do have a l/f noise behaviour that will be dominant at frequencies Fig. 3: ID p-U sound intensity probe (The under 500Hz [SI. Because the differential microphone and Microjlown are a half inch pressure is measured to determine the particle in diameter). velocity, two microphones are used, the total The Microflown has a first order frequency noise will increase by a factor 42. This is behaviour. For low frequencies (f<300Hz) the depicted in Fig. 2. A plane wave with a sound frequency response will be flat and the phase intensity level of 94dB is offered to the p-p shift will be zero degrees. For higher probe. The signal (that will be used to calculate frequencies the (P3kHz) the frequency the particle velocity) is produced by the response will be exactly -6dB/oct and the phase subtraction of both pressure microphone shift will be -90 degrees. At its corner outputs. frequency the Microflown has a -3dB response Output voltages of a P-P probe and a phase shift of -45 degrees. It is not very difficult to correct the frequency behaviour of the Microflown electronically. BANDWIDTH(P-U) IOOpV - The bandwidth of a Microflown and a Non reactive field pressure microphone can not be compared Strona reactive field easily. Above the corner frequency a pressure 10pV - microphone can not be used. The Microflown 74dB however has an exact first order frequency 1 1- I behaviour. Therefore the Microflown can be used above its corner frequency. The present 100nV value of the corner frequency is 1kHz. 31.6nV For sound intensity purposes the lowest usable frequency will be determined by the pressure microphone and can be found lower Fig. 2: Noise output voltages in V/&z and ,i&uls due to 94dB SIL than IHz. It is hard to give a distinct high frequency As can be seen in Fig 2, when the frequency limit of a p-U probe.
Load more

Recommended publications
  • Definition and Measurement of Sound Energy Level of a Transient Sound Source
    J. Acoust. Soc. Jpn. (E) 8, 6 (1987) Definition and measurement of sound energy level of a transient sound source Hideki Tachibana,* Hiroo Yano,* and Koichi Yoshihisa** *Institute of Industrial Science , University of Tokyo, 7-22-1, Roppongi, Minato-ku, Tokyo, 106 Japan **Faculty of Science and Technology, Meijo University, 1-501, Shiogamaguti, Tenpaku-ku, Nagoya, 468 Japan (Received 1 May 1987) Concerning stationary sound sources, sound power level which describes the sound power radiated by a sound source is clearly defined. For its measuring methods, the sound pressure methods using free field, hemi-free field and diffuse field have been established, and they have been standardized in the international and national stan- dards. Further, the method of sound power measurement using the sound intensity technique has become popular. On the other hand, concerning transient sound sources such as impulsive and intermittent sound sources, the way of describing and measuring their acoustic outputs has not been established. In this paper, therefore, "sound energy level" which represents the total sound energy radiated by a single event of a transient sound source is first defined as contrasted with the sound power level. Subsequently, its measuring methods by two kinds of sound pressure method and sound intensity method are investigated theoretically and experimentally on referring to the methods of sound power level measurement. PACS number : 43. 50. Cb, 43. 50. Pn, 43. 50. Yw sources, the way of describing and measuring their 1. INTRODUCTION acoustic outputs has not been established. In noise control problems, it is essential to obtain In this paper, "sound energy level" which repre- the information regarding the noise sources.
    [Show full text]
  • 21-4 Sound and Sound Intensity One Way to Produce a Sound Wave in Air Is to Use a Speaker
    Answer to Essential Question 21.3: Doubling the angular frequency, ", causes the frequency to double in part (a). This, in turn, means that that wave speed must double, in part (b). In part (c), the tension is proportional to the square of the speed, so the tension is increased by a factor of 4. In part (e), the maximum transverse speed is proportional to ", so the maximum transverse speed doubles. Finally, in part (f) we get a completely different value, y = – 0.39 cm. 21-4 Sound and Sound Intensity One way to produce a sound wave in air is to use a speaker. The surface of the speaker vibrates back and forth, creating areas of high and low density (corresponding to pressure a little higher than, and a little lower than, standard atmospheric pressure, respectively) in the region of air next to the speaker. These regions of high and low pressure (the sound wave) travel away from the speaker at the speed of sound. The air molecules, on average, just vibrate back and forth as the pressure wave travels through Medium Speed of sound them. In fact, it is through the collisions of air molecules that the sound wave is propagated. Because air molecules are not coupled Air (0°C) 331 m/s together, the sound wave travels through gas at a relatively low Air (20°C) 343 m/s speed (for sound!) of around 340 m/s. As Table 21.1 shows, the Helium 965 m/s speed of sound in air increases with temperature. Water 1400 m/s Steel 5940 m/s For other material, such as liquids or solids, in which there Aluminum 6420 m/s is more coupling between neighboring molecules, vibrations of the Table 21.1: Values of the speed of atoms and molecules (that is, sound waves) generally travel more sound through various media.
    [Show full text]
  • Sound Intensity and Power
    Sound intensity and power Professor Phil Joseph Departamento de Engenharia Mecânica IMPORTANCE OF SOUND INTENSITY AND SOUND POWER MEASUREMENT . Sound pressure is the quantity usually used to quantify sound fields. However, it is often satisfactory as an measure of source because the pressure propagates as a wave which, due to multi-path interference, may lead to fluctuations with observer position. Sound pressure, unlike measures of sound energy, are not conserved. Performance of noise control systems often specified in terms of energy, e.g., transmission loss, absorption coefficient. INSTANTANEOUS INTENSITY Instantaneous sound intensity I(t) is the rate of acoustic energy flowing through unit area in unit time (Wm-2). If, in a point in space, the acoustic pressure p(t) produces at the same point a particle velocity u(t), the rate at which work is done on the fluid per unit area I(t) at time t is given by It ptut Note that I is a vector quantity in the direction of the particle velocity u ‘PROOF’ The work done on the fluid by Force F acting over a distance d in the direction of the force is Fd The work done per unit area A in unit time T, i.e., the sound intensity, is given by F d I x pu A T EXAMPLES FOR WHICH SOUND INTENSITY AND MEAN SQUARE PRESSURE ARE SIMPLY RELATED 1. Plane progressive waves 2. Far field of a source in free field 3. Hemi-diffuse field However, in general there is no simple relation between intensity and pressure ENERGY CONSERVATION Net rate of change of energy = Rate of energy in – Rate of energy out E I I xy x xy y xy t x t In 3 - dimensions E I I I .It 0 .I x y z t x x x RELATIONSHI[P BETWEEN SOUND IINTENSITY AND SOURCE SOUND POWER Applying Gauss's divergence theorem .A dV A.nˆ dS V S to E .I 0 t gives E W dV I.nˆ dS V t S GENERAL PROPERTIES OF SOUND INTENSITY FIELDS Sound intensity (sometimes called sound power flux density) is a vector quantity acting in the direction of the particle velocity vector u(t).
    [Show full text]
  • The Human Ear  Hearing, Sound Intensity and Loudness Levels
    UIUC Physics 406 Acoustical Physics of Music The Human Ear Hearing, Sound Intensity and Loudness Levels We’ve been discussing the generation of sounds, so now we’ll discuss the perception of sounds. Human Senses: The astounding ~ 4 billion year evolution of living organisms on this planet, from the earliest single-cell life form(s) to the present day, with our current abilities to hear / see / smell / taste / feel / etc. – all are the result of the evolutionary forces of nature associated with “survival of the fittest” – i.e. it is evolutionarily{very} beneficial for us to be able to hear/perceive the natural sounds that do exist in the environment – it helps us to locate/find food/keep from becoming food, etc., just as vision/sight enables us to perceive objects in our 3-D environment, the ability to move /locomote through the environment enhances our ability to find food/keep from becoming food; Our sense of balance, via a stereo-pair (!) of semi-circular canals (= inertial guidance system!) helps us respond to 3-D inertial forces (e.g. gravity) and maintain our balance/avoid injury, etc. Our sense of taste & smell warn us of things that are bad to eat and/or breathe… Human Perception of Sound: * The human ear responds to disturbances/temporal variations in pressure. Amazingly sensitive! It has more than 6 orders of magnitude in dynamic range of pressure sensitivity (12 orders of magnitude in sound intensity, I p2) and 3 orders of magnitude in frequency (20 Hz – 20 KHz)! * Existence of 2 ears (stereo!) greatly enhances 3-D localization of sounds, and also the determination of pitch (i.e.
    [Show full text]
  • Ptechreview-02-1937
    FEBRUÄRY 1937 47 OCTAVES AND DECIBELS By R. VERMEULEN. Summary. With the aid of practical data, the relationships are discussed between the acoustic magnitudes: Pitch' interval and loudness, and the corresponding physical mag- nitudes:' frequency and sound intensity. The object of this article is to emphasise that the logarithmic units, octaves and decibels, should be given preference in acoustics for denoting physical magnitudes. ' Why is a preference shown in acoustics and In music, where without any close insight into the associated subjects for logarithmic scales and are physics of sound the pitch has always been denoted even new units introduced to permit the employment in musical scores by notes, the concept "musical of such scales?' The use of logarithmic scales in or pitch interval" has been introduced to repr,esent acoustics is justified from a consideration of the a specific difference in pitch. The most important characteristics of the human ear, apart from pitch interval is the 0 c t a v e: Two tones which many other advantages offered in both this and are at an interval of an octave have-such a marked other subjects. Reasons for this are that to a natural similarity that musicians have not consid- marked extent' acoustic measurements, and par- ered it necessary to introduce different names for ticularly technical sound measurements, represent them, but have merely distinguished them by attempts to find a substitute for direct judgement means of indices. In addition to the octave, there by means of the ear. An instructive example of are pitch intervals, such as the fifth, fourth and this is offered in the determination of the charac- several others, which are similarly perfectly natural teristics of a loudspeaker, ill which not only must and self-evident, not only because two tones which the reproduced music arid speech be analysed differ from each other by such a pitch interval critically but inter alia the loudness also deter- harmonise with each other, but also, and this is mined, i.e.
    [Show full text]
  • Lecture 6 Sound Waves
    LECTURE 6 SOUND WAVES Instructor: Kazumi Tolich Lecture 6 2 ¨ Reading chapter 14.4 to 14.5 ¤ Speed of sound ¤ Frequency of a sound wave ¤ Sound intensity ¤ Intensity level & human perception of sound Quiz: 1 3 ¨ Does a longitudinal wave, such as a sound wave, have an amplitude? A. yes B. no C. it depends on the medium the wave is in Quiz: 6-1 answer 4 ¨ Yes ¨ Both transverse and longitudinal waves have all of these properties: ¤ wavelength ¤ frequency ¤ amplitude ¤ velocity ¤ period Sound waves/Demo: 1 5 ¨ Sound waves are carried by oscillating molecules in air (or other medium carrying the sound), causing the density and pressure of the air to oscillate. ¨ The speed of sound is different in different materials; in general, the denser the material, the faster sound travels through it. ¨ In this class, we will use the speed of sound in air to be 343 m/s. ¨ Demo: Siren in Vacuum Quiz: 2 6 ¨ When a sound wave passes from air into water, what properties of the wave will change? Choose all that apply. A. The frequency B. The wavelength C. The speed of the wave Quiz: 6-2 answer 7 A. The frequency B. The wavelength C. The speed of the wave ¨ Wave speed must change (different medium). ¨ Frequency does not change (determined by the source). ¨ Now, � = �� and because � has changed and � is constant then � must also change. Frequency of a sound wave/Demo: 2 8 ¨ The frequency of a sound wave is its pitch. ¨ Sound waves can have any frequency; the human ear can hear sounds between about 20 Hz and 20,000 Hz.
    [Show full text]
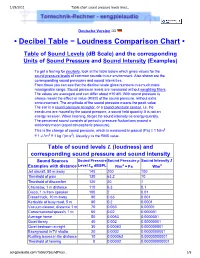
  • Table Chart Sound Pressure Levels Level Sound Pressure
    1/29/2011 Table chart sound pressure levels level… Deutsche Version • Decibel Table − Loudness Comparison Chart • Table of Sound Levels (dB Scale) and the corresponding Units of Sound Pressure and Sound Intensity (Examples) To get a feeling for decibels, look at the table below which gives values for the sound pressure levels of common sounds in our environment. Also shown are the corresponding sound pressures and sound intensities. From these you can see that the decibel scale gives numbers in a much more manageable range. Sound pressure levels are measured without weighting filters. The values are averaged and can differ about ±10 dB. With sound pressure is always meant the effective value (RMS) of the sound pressure, without extra announcement. The amplitude of the sound pressure means the peak value. The ear is a sound pressure receptor, or a sound pressure sensor, i.e. the ear-drums are moved by the sound pressure, a sound field quantity. It is not an energy receiver. When listening, forget the sound intensity as energy quantity. The perceived sound consists of periodic pressure fluctuations around a stationary mean (equal atmospheric pressure). This is the change of sound pressure, which is measured in pascal (Pa) ≡ 1 N/m2 ≡ 1 J / m3 ≡ 1 kg / (m·s2). Usually p is the RMS value. Table of sound levels L (loudness) and corresponding sound pressure and sound intensity Sound Sources Sound PressureSound Pressure p Sound Intensity I Examples with distance Level Lp dBSPL N/m2 = Pa W/m2 Jet aircraft, 50 m away 140 200 100 Threshold of pain
    [Show full text]
  • Lecture 1-2: Sound Pressure Level Scale
    Lecture 1-2: Sound Pressure Level Scale Overview 1. Psychology of Sound. We can define sound objectively in terms of its physical form as pressure variations in a medium such as air, or we can define it subjectively in terms of the sensations generated by our hearing mechanism. Of course the sensation we perceive from a sound is linked to the physical properties of the sound wave through our hearing mechanism, whereby some aspects of the pressure variations are converted into firings in the auditory nerve. The study of how the objective physical character of sound gives rise to subjective auditory sensation is called psychoacoustics. The three dimensions of our psychological sensation of sound are called Loudness , Pitch and Timbre . 2. How can we measure the quantity of sound? The amplitude of a sound is a measure of the average variation in pressure, measured in pascals (Pa). Since the mean amplitude of a sound is zero, we need to measure amplitude either as the distance between the most negative peak and the most positive peak or in terms of the root-mean-square ( rms ) amplitude (i.e. the square root of the average squared amplitude). The power of a sound source is a measure of how much energy it radiates per second in watts (W). It turns out that the power in a sound is proportional to the square of its amplitude. The intensity of a sound is a measure of how much power can be collected per unit area in watts per square metre (Wm -2). For a sound source of constant power radiating equally in all directions, the sound intensity must fall with the square of the distance to the source (since the radiated energy is spread out through the surface of a sphere centred on the source, and the surface area of the sphere increases with the square of its radius).
    [Show full text]
  • Product Data: Sound Intensity Probe Sets
    Product Data Sound Intensity Probe Sets — Types 3583, 3584 Sound Intensity Microphone Pairs — Types 4178, 4197 Dual Preamplifier — Type 2682 USES: FEATURES: ❍ Measurement of sound intensity using two- ❍ Microphone pairs matched for phase and amplitude microphone technique, in accordance with IEC 1043 response Class 1 ❍ Individual calibration data ❍ Sound power measurements in accordance with ❍ 1 /3-octave centre frequency ranges: ISO 9614–1, ISO 9614–2, ECMA 160 and 3583: 20 Hz to 10 kHz ANSI S 12–12 3584: 20 Hz to 6.3 kHz ❍ Minimal shadow and diffraction effects ❍ Well-defined acoustical microphone separation The transducer is the first stage in many measurement chains. Its relia- bility determines the ultimate accura- cy of the system. This is especially so for sound intensity measurements with a two-microphone technique where stringent requirements are placed on the phase and sensitivity matching be- tween the probe microphones. Types 3583 and 3584 are two-micro- phone probe sets for measuring sound intensity with Brüel&Kjær’s range of sound intensity analyzers. These probe sets feature precision, phase and sensi- tivity matching between the probe micro- phones. All the probe sets are supplied with a 1/2″ Sound Intensity Microphone Probe Set Type 3583 in carrying case Pair Type 4197, enabling measurements between 1/3-octave centre frequencies of 20Hz and 6.3kHz. With 1/2″ micro- phones the probe sets comply with IEC1043 Class 1. Type 3583 also in- cludes a 1/4″ Microphone Pair Type 4178, extending the upper 1/3-octave centre fre- quency to 10kHz. The Remote Control Unit ZB0017 is part of Type 3584.
    [Show full text]
  • Sound Intensity Measurement
    This booklet sets out to explain the fundamentals of sound intensity measurement. Both theory and applica- tions will be covered. Although the booklet is intended as a basic introduction, some knowledge of sound pres- sure measurement is assumed. If you are unfamiliar with this subject, you may wish to consult our companion booklet "Measuring Sound". See page See page Introduction ........................................................................ 2 Spatial Averaging ...…......................................................... 15 Sound Pressure and Sound Power................................... 3 What about Background Noise? ....................................... 16 What is Sound Intensity? .................................................. 4 Noise Source Ranking ........................................................ 17 Why Measure Sound Intensity? ........................................ 5 Intensity Mapping .............................................…......... 18-19 Sound Fields ................................................................... 6-7 Applications in Building Acoustics .................................. 20 Pressure and Particle Velocity .......................................... 8 Instrumentation .................................................................. 21 How is Sound Intensity Measured? …......................... 9-10 Making Measurements ......................................…........ 22-23 The Sound Intensity Probe .............................................. 11 Further Applications and Advanced
    [Show full text]
  • Mezzo Sound Intensity Probe with Mezzo Intensity Analyzer Module
    Mezzo Sound Intensity Probe with Mezzo Intensity Analyzer Module User Guide – v1.5.0 2016-01-21 Soft dB Inc. 1040, Belvedere Avenue, Suite 215 Quebec (Quebec) Canada G1S 3G3 Toll free: 1-866-686-0993 (USA and Canada) E-mail: [email protected] Contents 1 Introduction ............................................................................................................................. 1 2 Specifications .......................................................................................................................... 2 2.1 Mezzo Sound Intensity Probe .................................................................................................................. 2 2.2 Mezzo Intensity Analyzer Module .......................................................................................................... 3 3 Setting up the Mezzo Sound Intensity Probe ........................................................................ 4 3.1 Mounting the microphones ..................................................................................................................... 4 3.1.1 G.R.A.S. 40GK-26CC Microphone Pair..................................................................................... 4 3.1.2 BSWA MP201-MA221 Microphone Pair ................................................................................. 5 3.2 Installing the windscreen .......................................................................................................................... 6 3.3 Connecting the probe to the computer .................................
    [Show full text]
  • Sound Fields
    Ch01-H6526.tex 19/7/2007 14: 2 Page 1 Chapter 1 Sound fields 1.1 Introduction his opening chapter looks at aspects of sound fields that are particularly relevant to sound insulation; the reader will also find that it has general applications to room Tacoustics. The audible frequency range for human hearing is typically 20 to 20 000 Hz, but we generally consider the building acoustics frequency range to be defined by one-third-octave-bands from 50 to 5000 Hz. Airborne sound insulation tends to be lowest in the low-frequency range and highest in the high-frequency range. Hence significant transmission of airborne sound above 5000 Hz is not usually an issue. However, low-frequency airborne sound insulation is of partic- ular importance because domestic audio equipment is often capable of generating high levels below 100 Hz. In addition, there are issues with low-frequency impact sound insulation from footsteps and other impacts on floors. Low frequencies are also relevant to façade sound insu- lation because road traffic is often the dominant external noise source in the urban environment. Despite the importance of sound insulation in the low-frequency range it is harder to achieve the desired measurement repeatability and reproducibility. In addition, the statistical assump- tions used in some measurements and prediction models are no longer valid. There are some situations such as in recording studios or industrial buildings where it is necessary to consider frequencies below 50 Hz and/or above 5000 Hz. In most cases it should be clear from the text what will need to be considered at frequencies outside the building acoustics frequency range.
    [Show full text]