Cyclotron Specials
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Consortium of Swiss Academic Libraries the Consortium of Swiss Academic Libraries
Research Collection Other Conference Item Times change and we change with them: the Consortium of Swiss Academic Libraries the Consortium of Swiss Academic Libraries Author(s): Boutsiouci, Pascalia Publication Date: 2015 Permanent Link: https://doi.org/10.3929/ethz-a-010439524 Rights / License: In Copyright - Non-Commercial Use Permitted This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library TIMES CHANGE AND WE CHANGE WITH THEM The Consortium of Swiss Academic Libraries ICoASL – 4th International Conference of Asian Special Libraries 2015 Pascalia Boutsiouci, Seoul, April 23 of 2015 AGENDA 1 Overview Switzerland and Higher Education 2 Overview Consortium of Swiss Academic Libraries 3 Our business – range of activity 4 Cooperation with our partner libraries 5 projects © Consortium of Swiss Academic Libraries | 2015 2 Overview Switzerland 1 and Higher Education © Consortium of Swiss Academic Libraries | 2015 3 THE LANDSCAPE Switzerland lies in the heart of Europe 8.2 million people 26 cantons Four official languages Matterhorn, Zermatt (4,478 m/14,692 ft) / Image source: http://www.zermatt.ch/Media/Pressecorner/Fotodatenbank/Matterhorn/Sicht-aufs- . German (66%) Matterhorn-vom-Gornergrat . French (23%) . Italian (9%) . Rheto- Romanic (1%) Image source: http://en.wikipedia.org/wiki/Switzerland#/media/File:Europe-Switzerland.svg © Consortium of Swiss Academic Libraries | 2015 4 SWITZERLAND = CONFOEDERATIO HELVETICA = CH Federal parliamentary republic consisting of 26 cantons wth Bern as the seat of the federal authorities Germany France Liechtenstein Austria Italy Image source:http://de.wikipedia.org/wiki/Datei:Switzerland,_administrative_divisions_-_de_-_colored.svg © Consortium of Swiss Academic Libraries | 2015 5 HIGHER EDUCATION IN SWITZERLAND Official Higher Education Institutions 10 Cantonal Universities . -

Treating Cancer with Proton Therapy Information for Patients and Family Members Professor Dr
Treating Cancer with Proton Therapy Information for patients and family members Professor Dr. med. Damien Charles Weber, Dear readers Head and Chairman, Proton therapy is a special kind of radiation therapy. For many years now, patients Centre for Proton Therapy suffering from certain tumour diseases have successfully undergone proton radi- ation therapy at the Paul Scherrer Institute’s Centre for Proton Therapy. This brochure is intended to give a more detailed explanation of how proton ther- apy works and provide practical information on the treatment we offer at our facil- ity. We will include a step-by-step description of the way in which we treat deep- seated tumours. We will not deal with the treatment of eye tumours in this brochure. If you have further questions on the proton therapy carried out at the Paul Scherrer Institute, please do not hesitate to address these by getting in touch with our secretaries. Contact details are provided at the end of the brochure. 2 Contents 4 Radiation against cancer 10 Physics in the service of medicine 14 Four questions for Professor Dr. Tony Lomax, Chief Medical Physicist 16 Practical information on treatment at PSI 20 Four questions for Dr. Marc Walser, Senior Radiation Oncologist 22 In good hands during treatment 28 Four questions for Lydia Lederer, Chief Radiation Therapist 30 Treating infants and children 36 Children ask a specialist about radiation 38 PSI in brief Radiation against cancer 4 Because it can be used with great ac- The most important cancer therapies curacy, proton therapy is a particularly are: sparing form of radiation treatment • surgery (operation), with lower side effects. -

Annual Report 2018 Swiss Nanoscience Institute University of Basel
EINE INITIATIVE DER UNIVERSITÄT BASEL UND DES KANTONS AARGAU Annual Report 2018 Swiss Nanoscience Institute University of Basel Swiss Nanoscience Institute University of Basel Klingelbergstrasse 82 4056 Basel Switzerland www.nanoscience.ch The Swiss Nanoscience Institute (SNI) is a research initiative of the Canton of Aargau and the University of Basel. Swiss Nanoscience Institute Klingelbergstrasse 82 4056 Basel Switzerland www.nanoscience.ch Cover: Atomic force microscopic image of “nano-bone” molecules on a gold surface. The molecule is a buil- ding block for the formation of two-dimensional organic topological insulators (Rémy Pawlak, Department of Physics, University of Basel). © Swiss Nanoscience Institute, March 2019 Content 3 Foreword 4 Swiss Nanoscience Institute — The interdisciplinary center of excellence for nanosciences in Northwestern Switzerland 6 Network 8 News from the network 14 The Paul Scherrer Institute – 30 years old and a key partner on the SNI network 16 Nano Study Program 18 Glued wounds heal better – Tino Matter wins the prize for the best master’s thesis 20 Discussing science at SmallTalk – Students organize their own symposium about the block courses 22 PhD School 24 SNI PhD School – An excellent start of a scientific career 29 Multiple awards – Daniel Riedel wins several prizes 30 SNI Professors 32 Martino Poggio studies nanowires – These tiny wires with special properties have a variety of potential applications 34 Roderick Lim researches the transport processes and mechanical properties of cells – Promising -

Particle Accelerator Activities at the Paul Scherrer Institut
PSI Bericht Nr. 17-07 December 2017 Particle Accelerator Activities at the Paul Scherrer Institut Terence GARVEY Paul Scherrer Institut, Villigen, Switzerland 5232 Division of Large Research Infrastructures Invited paper presented at Les Journées Accélérateurs de la Société Française de Physique, Roscoff, 3rd – 6th October, 2017. Resumé Les Activités Accélérateur à l’Institut Paul Scherrer. L'Institut Paul Scherrer exploite deux complexes d'accélérateurs en tant que ‘centre- serveurs’ pour une grande communauté de chercheurs. Il s'agit de l'Accélérateur de Protons à Haute Intensité (HIPA) et de la Source de Lumière Suisse (SLS). HIPA est un cyclotron à protons de 590 MeV. Il sert à produire des neutrons par spallation pour la recherche en physique de la matière condensée et à produire des muons et d'autres particules secondaires pour la recherche en magnétisme et en physique des particules. Le SLS est un anneau de stockage d’électrons de 2,4 GeV utilisé comme source de rayonnement synchrotron de 3ème génération fournissant des photons pour une large gamme de disciplines scientifiques. En plus de ces deux installations, l'Institut met progressivement en service un laser à électrons libres en rayons X (SwissFEL) qui fournira aux chercheurs des impulsions femto-seconde intenses à partir d’une ligne de rayons X ‘dur’ (ARAMIS) et de rayons X ‘mou’ (ATHOS). L'Institut exploite également un cyclotron supraconductrice à 250 MeV (COMET) aux fins de la thérapie par proton. Le centre de thérapie a récemment été équipé d'un troisième « gantry » rotatif qui est en cours de mise en service. Un « upgrade » du système de radiofréquence de HIPA et des projets pour "SLS-2" seront présentés. -

2018 Research Slam
University of St.Gallen (HSG) Centro Latinoamericano-Suizo (CLS-HSG) Leading House for the Latin American Region Müller-Friedberg-Strasse 8 CH-9000 St.Gallen 2018 Research Slam Wednesday, December 19, 2018 / 10:30 to 17:10 hrs Tellstrasse 2, St.Gallen / Room 58-515 Seed Money Grants 2017 Research Merger 2018 Seed Money Grants 2018 Presentation Material of the Winning Projects The Funding Instruments SMG – Seed Money Grants 2017 + 2018 duration: 10 – 12 months grants: CHF 10’000 – CHF 25’000 applications received: 87 / projects awarded: 30 RM – Research Merger 2017 duration: 10 – 12 months grants: CHF 30’000 – CHF 50’000 applications received: 29 / projects awarded: 4 MOB – Mobility Grants 2018 duration: up to 3 months grants: up to CHF 8’000 applications received: 9 / projects awarded: 7 2018 Research Slam 2 / 22 Index Towards the detection of Earth analogues (TDEA). – SMG2017 Damien Ségransan, University of Geneva.............................................................................................................................. 5 Structural colours in natural and artificial multilayers. – SMG2017 Ullrich Steiner, University of Fribourg, Adolphe Merkle Institute .................................................................................. 5 In-operando control of nanoscale decoration of graphene and reduced graphene oxide by novel mini-reactors. – SMG2017 Ivo Utke, Empa, Eidgenössische Materialprüfungs- und Forschungsanstalt (EMPA) ................................................... 6 A dendrogeomorphic reconstruction of -

03 (15. Februar 2017)
2017/03 ISSN 1661-8211 | 117. Jahrgang | 15. Februar 2017 Redaktion und Herausgeberin: Schweizerische Nationalbibliothek NB, Hallwylstrasse 15, CH-3003 Bern Erscheinungsweise: halbmonatlich, am 15. und 30. jeden Monats Hinweise unter: http://ead.nb.admin.ch/web/sb-pdf/ ISSN 1661-8211 © Schweizerische Nationalbibliothek NB, CH-3003 Bern. Alle Rechte vorbehalten Inhaltsverzeichnis - Table des matières - Sommario - Cuntegn - Table of contents Inhaltsverzeichnis - Table des matières - 220 Bibel / Bible / Bibbia / Bibla / Bible....................................... 6 Sommario - Cuntegn - Table of contents 230 Christentum, christliche Theologie / Christianisme, théologie chrétienne / Cristianesimo, teologia cristiana / Cristianissem, teologia cristiana / Christianity and Christian theology..................6 000 Allgemeine Werke, Informatik, Informationswissenschaft / Informatique, information, 290 Andere Religionen / Autres religions / Altre religioni / Autras ouvrages de référence / Informatica, scienza religiuns / Other religions............................................................... 9 dell'informazione, generalità / Informatica, infurmaziun e referenzas generalas / Computers, information and general reference........................................................................................ 1 300 Sozialwissenschaften / Sciences sociales / Scienze sociali / Scienzas socialas / Social sciences.......................... 10 000 Allgemeine Werke, Wissen, Systeme / Généralités, savoir, systèmes / Generalità, sapere, sistemi / Generalitads, -

Booklet SSD27
Swiss Soft Days 27th Edition FORMULA The Swiss Soft Days is a one-day workshop taking place 2 times per year where around 20 speakers give short talks (~15 minutes) to introduce their research activities in a way specifically designed for a heterogeneous public. Besides well established scientific figures, the workshops are aimed at emerging researchers, especially assistant professors, post-docs and PhD students. The short duration of the talks and the SEM image of wrinkled cellulose colloids frequency of the meetings are meant to © Johannes Bergmann rapidly develop active, up-to-date communications and cover various inter- disciplinary areas of research. 8.6.2021 Swiss Soft Days 27th Edition Swiss Soft Days 27th Edition Program 12h00 Platform opening 15h30: Session 2 – Soft matter under deformation 12h20 Welcome Manolis Chatzigiannakis, ETHZ: Dynamic stabilisation of draining thin liquid films consisting of 12h30: Session 1 – Active and responsive materials polymer solutions Steven van Kesteren, ETHZ: Responsive colloidal Hamed Almohammadi, ETHZ: Flow-induced order– molecules as internally-controlled microswimmers order transitions in amyloid fibril liquid crystalline with multi-state dynamics tactoids Elena Sesé Sansa, EPFL: Emergent phase behavior of Dominic Gerber, ETHZ: What happens when a soft active Brownian disks in the presence of different material freeZes? alignment interaction symmetries 16h30: Poster (40 min) Boyang Zhou, PSI: Direct measurements of the pNipam Microgel Counter-ion Cloud via Small Angle Neutron Scattering -

First Operation of the Ultracold Neutron Source at the Paul Scherrer Institute
First operation of the ultracold neutron source at the Paul Scherrer Institute The UCN source team has demonstrated excellent functioning of all major subsystems of the new facility. Ultracold neutrons have been produced for the first time from this source and under full load. The performance was found as expected under the operational conditions. The construction of the PSI source for ultracold neutrons (UCN) has been completed. The new UCN source is the second spallation target station driven by the PSI ring cyclotron and designed to take macro-pulses of up to 8s of the full proton beam intensity (590MeV, >2mA). Neutrons are thermalized in a heavy water moderator, cooled down and converted to UCN in solid deuterium. The license to start full commissioning arrived on December 16. Between December 16 and 22, the source has been operated with the aim and duty to demonstrate the principle functioning of all major subsystems. Different modes of operation have been tested starting with 5ms short pulses ramping from 100µA to 1.8mA (operational limit of the accelerator at the time of testing), followed by continuous 10µA beam for mapping of the radiation field and dose rates around the biological shielding, especially in the experimental areas, and finally going to longer pulses starting from 500µA for 2s up to 1.8mA for 8s. The test of the whole accelerator chain and beam diagnostics was very successful and the desired pulses were reliably delivered. Long intense pulses of the 1MW beam always had 5ms pilot pulses running a few seconds ahead and guaranteeing the perfect adjustment of the proton beamline. -
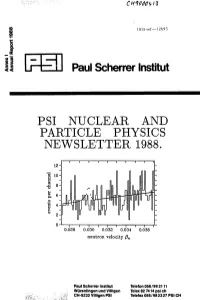
I Ll PSI NUCLEAR and PARTICLE PHYSICS NEWSLETTER 1988
cIo INIS-mf—12695 I ll SS Paul Scherrer Institut PSI NUCLEAR AND PARTICLE PHYSICS NEWSLETTER 1988. 0.028 0.030 0.032 0.034 0.036 neutron velocity 0n Paul Scherrer Institut Telefon 056/99 2111 WurenlingenundVilllgen Telex827414psich CH-5232 Villigen PSI Telefax 056/982327 PSI CH PAUL SCHERRER INSTITUTE Research Department Fl: Particule and Nuclear Physics CH-5232 Viliigen PSI Switzerland Telephone 056/99 2111 Telegram PSI Viliigen Telex 82 7419 psi ch Telefax 056/993294 PSI/IMP CH PSI NUCLEAR AND PARTICLE PHYSICS NEWSLETTER 1988 Editor: Reinhard Frosch, PSI. January 1989. Production and distribution: PSI Documentation and Information Group. Introduction Because of the fusion of EIR and SIN in January 1988, I this year's Newsletter differs from the previous editions. 12- The contributions on solid-state physics and chemistry i appear in a separate volume. The present volume con- O tains reports on nuclear and particle physics experi- D ments supported fay the Fl division of PSI. The ma- cnanne r C jority of the contributions are concerned with experi- ) <7 ments using the Philips cyclotron or the 590 Me V ring pe s accelerator. c As before, the contributions have not been refereed and fl must not be quoted without previous consultation with Api the authors. The spokespersons are indicated by super- FIB scripts 'S' following their names in the headings of the 0- contributions. 0.028 0.030 0.032 0.034 0.036 The figure on the right is from an experimental search neutron velocity Bn for the neutral pion decay 7r" —. e+e~ . -

B. Steinmann, M. Borkovec
POLYMERS AND COLLOIDS DIVISION 772 doi:10.2533/chimia.2008.772 CHIMIA 2008, 62, No. 10 EDITORIAL An organization to bring together scientists dealing with macromolecules, polymers and colloids has been present in Switzerland for more than 20 years under the name PGS, Polymer Group of Switzerland. This group was founded by Prof. P. Pino in 1984 with the aim to represent the Swiss polymer community within the newly founded European Polymer Federation. Over the years, it has become clear that such a relatively small group has a hard time to survive as an independent organization. On the other hand, as the grow- ing importance of polymer and colloid science also in Swiss industries and academia was recognized, the Swiss Chemical Society (SCS) expressed the desire to provide more visibility to these areas. In fact, all other important na- tional chemical societies have subgroups or divisions of macromolecular and/ or colloid science, for example the ‘Fachgruppe Makromolekulare Chemie’ of the German Society of Chemists (GdCh), the ‘Macro Group UK’, ‘Colloid and Interface Science Group’ and ‘Particle Characterisation Group’ of the Royal Society of Chemistry or the ‘Division Polymères’ and ‘Groupe Formulation’ of the French Chemical Society. The division ‘Polymer Chemistry’ of the Ameri- can Chemical Society is even the second largest division of the society with more than 8000 members, and the division of ‘Colloid and Surface Chemistry’ has another 2500 members! Discussions about possibilities of closer cooperation resulted finally in the decision to include the PGS into SCS as a new Polymers and Colloids Divi- sion. This Division is now reality and our efforts are focussed on the integration of the group into the SCS, the creation of synergies between the divisions and on the organization of exciting activities in order to become a center of attraction and reference for the Swiss and international polymer and colloid communities. -

Paul Scherrer Institute
WIR SCHAFFEN WISSEN – HEUTE FÜR MORGEN Research at the Paul Scherrer Institute The Institute The Paul Scherrer Institute PSI is a re- search institute for natural and engineer- ing sciences, conducting cutting-edge research in the fields of matter and materials, energy and the environment and human health. By performing fun- damental and applied research, we work on sustainable solutions for major challenges facing society, science and economy. PSI develops, constructs and operates complex large research facilities. Every year more than 2500 guest scientists from Switzerland and around the world come to us. Just like PSI’s own researchers, they use our unique facilities to carry out experi- ments that are not possible anywhere PSI – a place of dialogue else. PSI is committed to the training PSI would like to bring the world of of future generations. Therefore about research closer to the general public. one quarter of our staff are post-docs, Come to our Visitor Centre – the post-graduates or apprentices. Alto- psi forum – and use the opportunity gether PSI employs 2100 people, thus to view the large research facilities during a guided tour. Teachers can being the largest research institute in get a taste of research, along with their Switzerland. school classes, during a whole day in the school laboratory, iLab. We look A bird’s-eye view of forward to seeing you! Paul Scherrer Institute. Getting to PSI from Koblenz / Waldshut (DE) AARE http://www.psi.ch/ PSI East Tegerfelden from Böttstein Böttstein P from how-to-find-us East Entrance Würenlingen P Auditorium Paul Scherrer Institute Bus: From Brugg railway P iLab P Würenlingen station (Number 376 West Entrance P psi forum PSI Education Centre Brugg–Döttingen) P Villigen AARE PSI West Restaurant Oase Stilli Siggenthal Station Car: Main roads from from Villigen Center for Proton Therapy Remigen Brugg to Koblenz, Untersiggenthal N Lauffohr or Baden to Koblenz LIMMAT Turgi Obersiggenthal Ennetbaden Brugg REUSS Windisch Baden AARE Exit Wettingen Hausen b. -

Overview Paul Scherrer Institute
Overview • Protontherapy @ PSI • Controls and Safety To promote excellency in patient care and innovative proton treatment – Concept – Implementation • Patient Safety System Therapy Control and Patient Safety Martin Grossmann Centre for Proton Therapy, Paul Scherrer Institute, Villigen, Switzerland Paul Scherrer Institut • 5232 Villigen PSI Paul Scherrer Institute PROScan facility at PSI OPTIS2 590 MeV proton cyclotron SwissFEL 250 MeV proton cyclotron COMET Gantry 1 Proton therapy Synchrotron light source Gantry 2 Paul Scherrer Institut • 5232 Villigen PSI Paul Scherrer Institut • 5232 Villigen PSI 1 Superconducting cyclotron with intensity modulation I Degrader and beam line for energy selection E Cyclotron COMET Varian/Accel Degrader (carbon 250 MeV protons Deflector plate for wedges in vacuum) fast beam current and laminated beam regulation ~ 50 ms line for fast energy changes < 80 ms Paul Scherrer Institut • 5232 Villigen PSI Paul Scherrer Institut • 5232 Villigen PSI Controls & safety Paul Scherrer Institut • 5232 Villigen PSI Paul Scherrer Institut • 5232 Villigen PSI 2 PSI’s concept for patient safety #1: NO RADIATION ACCIDENT • No serious overdose should be delivered to the patient • Serious: >5% of total prescribed dose (60 Gy), i.e. 3 Gy • Definition of safety goals • Description of technical/operational measures Paul Scherrer Institut • 5232 Villigen PSI Paul Scherrer Institut • 5232 Villigen PSI #2: NO ERROR IN THE #3: NO ERROR IN DELIVERED DOSE DOSE POSITION • No incorrect dose should be delivered • The dose must be applied