Metric-Distortion Bounds Under Limited Information
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

There Aren't Enough Bobbleheads in the World
Feet Up Friday – There aren’t enough bobbleheads in the world Christine: We’ve just had two back-to-back races and now we’ve got back-to-back Feet up Friday’s, this almost never happens anymore. Mr C: It feels like we are underway, the season is go and it’s been non-stop from the first green flag of the year. This is the first break we’ve had, a little bit of downtime for Sidepodcast, but still we are recording a new show for you, that’s how hard we are working this year. Christine: But after two races in a row we’ve got three weeks off now and then there’s another two races and then there’s another three weeks off, it’s just weird scheduling this calendar. Mr C: It’s a crazy calendar, but it makes sense for the people who have to endure it. If you are a Formula 1 team who has to pay personnel to go off overseas, back-to-back races makes a lot of sense. You can cram in a lot of action, you can cram in a lot of racing in a fortnight, and then you can get back to base and save yourself a lot of money and in these troubled economic times, that is essential, so you can’t hold in against… you cannot hold the calendar against the people who have to go out there and live it. Christine: No. And having three weeks off gives us plenty of time to ponder everything that happened in Malaysia because my goodness that was a controversial race. -

DTM Zandvoort Zandvoort, Length 4307 M 13
DTM Zandvoort Zandvoort, length 4307 m 13. - 15.07.2018 DTM Result race 1, 14.07.2018 -Reg.No.: 0301.18.219 Rk No ENTRANT/DRIVER CAR LAPS TIME GAP INT km/h BEST IN 1 2 Mercedes-AMG Motorsport PETRONAS Gary Paffett (GBR) Mercedes-AMG C 63 DTM 34 57:29.724 152.817 1:32.317 4 2 3 Mercedes-AMG Motorsport REMUS 01.422 Paul Di Resta (GBR) Mercedes-AMG C 63 DTM 34 57:31.146 01.422 152.754 1:32.486 5 3 22 SILBERPFEIL Energy Mercedes-AMG Motorsport 00.443 Lucas Auer (AUT) Mercedes-AMG C 63 DTM 34 57:31.589 01.865 152.735 1:32.534 17 4 94 Mercedes-AMG Motorsport PETRONAS 00.425 Pascal Wehrlein (DEU) Mercedes-AMG C 63 DTM 34 57:32.014 02.290 152.716 1:32.381 5 5 4 Audi Sport Team Abt Sportsline 00.407 Robin Frijns (NLD) Aral Ultimate Audi RS 5 DTM 34 57:32.421 02.697 152.698 1:32.497 11 6 16 BMW Team RMR 01.425 Timo Glock (DEU) DEUTSCHE POST BMW M4 DTM 34 57:33.846 04.122 152.635 1:32.645 7 7 11 BMW Team RMG 02.741 Marco Wittmann (DEU) BMW Driving Experience M4 DTM 34 57:36.587 06.863 152.514 1:32.704 7 8 15 BMW Team RMG 00.338 Augusto Farfus (BRA) Shell BMW M4 DTM 34 57:36.925 07.201 152.499 1:32.814 9 9 47 BMW Team RBM 00.666 Joel Eriksson (SWE) BMW M4 DTM 34 57:37.591 07.867 152.469 1:32.892 18 10 53 Audi Sport Team Rosberg 00.681 Jamie Green (GBR) Hoffmann Group Audi RS 5 DTM 34 57:38.272 08.548 152.439 1:32.560 5 11 28 Audi Sport Team Phoenix 00.337 Loic Duval (FRA) Audi Sport RS 5 DTM 34 57:38.609 08.885 152.425 1:32.428 5 12 7 BMW Team RBM 01.214 Bruno Spengler (CAN) BMW Bank M4 DTM 34 57:39.823 10.099 152.371 1:33.098 9 13 48 SILBERPFEIL -
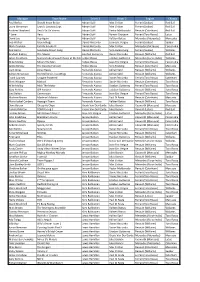
Manager Team Name Driver 1 Driver 2 Engine Chassis Paul Barker
Manager Team Name Driver 1 Driver 2 Engine Chassis Paul Barker Should Know Better Adrian Sutil Max Chilton Ferrari (Sauber) Red Bull Laura Stevenson Laura's Luscious Laps Adrian Sutil Max Chilton Ferrari (Sauber) Red Bull Andrew Shepherd Veci's Va Va Vooms Adrian Sutil Pastor Maldonado Renault (Caterham) Red Bull P Lane Aero Adrian Sutil Roman Grosjean Ferrari (Toro Rosso) Lotus David Lee Yep Again Adrian Sutil Valtteri Bottas Mercedes (Mercedes) Mercedes Bob Walker Groundhogs Daniel Ricciardo Jean-Eric Vergne Ferrari (Sauber) Sauber Mark Goulden Eat My Smoke III Daniel Ricciardo Max Chilton Mercedes (McLaren) Force India Rod Harris Sandiacre Street Gang Daniel Ricciardo Nico Hulkenberg Ferrari (Sauber) Williams Graham Bickley The Master Esteban Gutterrez Daniel Ricciardo Renault (Williams) Red Bull Julian Meetham Seemed Like A Good Choice at the timeFelipe Massa Esteban Gutterrez Mercedes (Force India) Williams Mike Molloy Mike's The Man Felipe Massa Jean-Eric Vergne Ferrari (Toro Rosso) Force India Jackie Bickley The Devoted Servant Felipe Massa Nico Rosberg Renault (Caterham) Marussia Liam Jones Jonez Races Fernando Alonso Adrian Sutil Renault (Williams) Williams Adrian Stevenson Red Bull Gives You Wings Fernando Alonso Adrian Sutil Renault (Williams) Williams Frank Caumes Lasagne Powered Fernando Alonso Daniel Ricciardo Ferrari (Toro Rosso) Caterham Chris Wingate Mallard Fernando Alonso Daniel Ricciardo Renault (Caterham) Toro Rosso Mike Molloy Mick The Motor Fernando Alonso Esteban Gutterrez Ferrari (Toro Rosso) Toro Rosso Gary Perkins -

Charles LECLERC (Ferrari)
Press Information 2019 Bahrain Grand Prix Saturday Press Conference Transcript 30.03.2019 DRIVERS 1 – Charles LECLERC (Ferrari) 2 – Sebastian VETTEL (Ferrari) 3 – Lewis HAMILTON (Mercedes) TRACK INTERVIEWS (Conducted by Paul Di Resta) Q: Charles, it’s your first ever pole position in Formula One, your second grand prix with Ferrari, you’ve looked in control all weekend, and you’ve got the job done. Charles LECLERC: Yeah, I’m extremely happy. Obviously in the last race I was not very happy with my qualifying – I did some mistakes in Q3 – and I really worked hard to try to not do the same mistakes here. It seems we did quite a good job, a front-row lockout and yeah, extremely happy. Q: How hard is it to come to grand prix tracks and be up against a four-time world champion in the same car and try and get that task and take that [pole]? CL: It’s obviously extremely hard because Seb is an amazing driver and I’ve learned a lot from him and I will probably learn all year long with him. But today I am very happy to be in front of him, so yeah, it’s a good day for me. Q: And the plan tonight. CL: Oh, going to sleep and work hard for the race tomorrow. Q: Sebastian, you line up on the first row of the grid. You had to use an extra set of tyres in Q2. Did that compromise your last run and leave a bit of safety there? Sebastian VETTEL: Yeah, of course. -
Amber Lounge Celebrity Yacht Abu Dhabi
AMBER LOUNGE CELEBRITY YACHT ABU DHABI AMBER LOUNGE ABU DHABI CELEBRITY RACE VIEWING YACHT RETURNING TO YAS MARINA iN 2015 After two incredibly successful seasons in 2013 & 2014, the Amber Lounge hospitality yacht will again thrill guests with its ultimate luxury weekend experience offering prime track views, F1 driver appearances, an all-day open bar, sublime buffets, goodie bags with team merchandise and VIP entrance to the famed Amber Lounge Party. Perfectly situated in the hub of Yas Marina - offering superb views of all the action on and off the track! The Amber Lounge Yacht plays host to international celebrities, socialites, sporting personalities and VIP guests… where business and pleasure become one. Guests will enjoy a lavish weekend with impeccable service and personal touches that will certainly leave a lasting impression. THE VIP PACKAGE INCLUDES: Race Viewing Saturday & Sunday Weekend Marina passes F1 Driver Appearances – Exclusive Interviews & Autograph Signing Gourmet Buffet Lunch Light Evening Buffet Dinner Open Champagne Bar Goodie Bags with official Team Merchandise Amber Lounge Opening Party - Saturday Night Access to the Yas Island concerts on Saturday & Sunday 2-DAY PACKAGE – USD 4950 PER PERSON Complete Your GP Weekend & Stay On-Board in One of Our Luxury Cabins - all inclusive 3 day packages – please enquire Previous F1 driver appearances have included; Romain Grosjean, Adrian Sutil, Felipe Massa, Paul di Resta, David Coulthard, Mika Hakkinen, Jerome d’Ambrosio, Eddie Irvine, Heikki Kovalainen, Bruno Senna, Vitantonio Luizzi, Giancarlo Fisichella, Esteban Ocon, Eddie Jordan. Previous guests include; Taio Cruz, John Martin, Justin Bieber, Kim Kardashian, Kellan Lutz, Jennifer Lawrence, Vanessa Hudgens, Eva Simons, Labrinth, Gareth Bale, Emile Heskey, Pixie Lott, Rachel Hunter, Sugababes, Pete Tong, Kris Humphries, Matthew Williamson, Estelle Swaray, Far East Movement. -

Pirelli: Low Degradation on a Demanding Track
PIRELLI: LOW DEGRADATION ON A DEMANDING TRACK Monza, September 8, 2012 – McLaren has claimed its third one-two in qualifying this year, thanks to pole position for Lewis Hamilton, who set a time of 1m24.010s at Monza, just ahead of his team mate Jenson Button. McLaren now equals the record of 61 one-two results in qualifying, held by Williams. Both drivers used the P Zero White medium tyre, which has been nominated along with the P Zero Silver hard tyre this weekend for the fastest circuit of the year. Once again, conditions were dry and warm for qualifying at Monza, with 43 degrees centigrade track temperature. Most drivers started the first qualifying session on the hard compound: only Marussia and HRT went for the medium compound. Some drivers were completing longer runs than usual during the session, with up to four flying laps as well as an in-lap and an out-lap in order to get the best out of the hard-wearing Silver tyre. Lotus stand-in Jerome D’Ambrosio was the first of the frontrunners to move onto the medium tyre in qualifying one, taking part in his first qualifying session since last year’s Brazilian Grand Prix. Ferrari’s Fernando Alonso was quickest in the first session, using the hard tyres. D’Ambrosio was also the only driver to start the second qualifying session on the hard tyre, while the other 16 competitors began the session on the P Zero White medium. Alonso was again quickest in the second session, having established his benchmark time on his first run with the mediums. -
Amber Lounge Returns to Austin
USPA CONTRIBUTING EDITORS REPORTER VERIFICATION OCTOBER 23, 2014 | 17:42 PM PHOTOS USPA STATISTICS REGISTER LOGIN CONTACT USPA HOME CORRESPONDENTS USPA NEWS NEWS SPORTS BUSINESS LIFESTYLE TECHNOLOGY POLITICS ARTS LOCAL USPA ENTERTAINMENT TRAVEL HEALTH AUTOMOBILES VIPS MUSIC MISCELLANEOUS DAREN FRANKISH Lifestyle AMBER LOUNGE RETURNS TO AUSTIN EUROPE JOON SHEN LEE EXCLUSIVE GP PARTY IN AUSTIN MALAYSIA Author: Joey Franco | Montreal, 09/27/2014, 16:45 Time 5187x read RAHMA-SOPHIA RACHDI NEWSRAMA CHRISTABELL LEONARD PETERS PROMEDIANEWS SHOW ALL Taboo at Amber Lounge Austin 2013 Source: Courtesy Amber Lounge USPA NEWS - Formula One's most exclusive party returns to Austin Texas for the second year in a row. For more than a decade, Amber Lounge has established itself as the most prestigious party in town entertaining F1 Drivers, Teams, Celebrities, and F1 aficionados. Last year, AL celebrated its 10th anniversary. Formula One's most exclusive party returns to Austin Texas for the second year in a row. For more than a decade, Amber Lounge has established itself as the most prestigious party in town entertaining F1 Drivers, Teams, Celebrities, and F1 aficionados. Last year, AL celebrated its 10th anniversary. Taboo at Amber Lounge Austin 2013 Last November, Amber Lounge Austin saw 14 Formula One drivers including Source: Courtesy Amber Lounge Mark Webber, Nico Rosberg, Jenson Button, Paul di Resta and Valtteri Bottas join international stars Gerard Butler, Gordon Ramsay, Adrian Grenier and Matt Leblanc to name a few to celebrate over the Grand Prix weekend, enjoying exclusive entertainment by Taboo of the Black Eyed Peas. This year, Amber Lounge Austin will open its doors exclusively for 2 nights: Saturday November 1st, and Sunday November 2nd. -

Simoncelli, Di Meglio and Dunlop Celebrate in Style!
THE OFFICIAL MAGAZINE OF DUNLOP MOTORSPORT IN TOUCH [ www.injection.tv ] ISSUE TEN, NOVEMBER 2008 Simoncelli, di Meglio and Dunlop celebrate in style! Marco Simoncelli and Alvaro Bautista have been the most consistent finishers in the MotoGP 250cc category, each scoring in 13 of the 15 races this year and are first and second in the riders' standings with one race remaining, in Valencia at the end of October. With his third place finish in Malaysia mid-October, seconds behind Bautista at the chequered flag, it was Simoncelli who was crowned the 2008 250cc champion and the Italian celebrated by completing a helmet-less victory lap around the track. Simoncelli has scored five wins to Bautista's four so far this year, but the Italian has consistently finished on the podium. Mid-season he was on devastating form, finishing second to Mika Kallio in France, and then winning the Spanish and German Grands Prix, finishing second in Britain, and third at the Dutch Grand Prix. Bautista had fallen far behind by the time the bikes lined up in Spain, having scored one win, but just 16 more points in the Mike di Meglio wins the Australian 125cc race and Dunlop's 12th straight category title opening six races. The Spaniard worked hard during the second half of the year, starting on his home ground where he was second to Simoncelli, and that led Dunlop celebrates another successful to a run of six straight podium finishes, culminating in victory in South Africa. The series was interrupted by Hurricane motorcycle racing season in 2008 Ike, which caused the cancellation of the Dunlop is celebrating another American 250cc Grand Prix, but in the Win number 50 came with performance.” next three races in Japan, Australia and fantastically successful season Valentino Rossi at the 1999 British “We thank the teams for putting Malaysia, Simoncelli again applied the in motor cycle racing. -
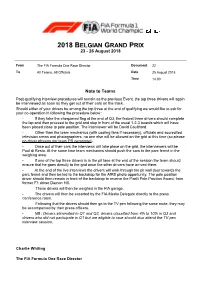
Race Director's Note – Post Qualifying Interviews
2018 BELGIAN GRAND PRIX 23 - 26 August 2018 From The FIA Formula One Race Director Document 22 To All Teams, All Officials Date 25 August 2018 Time 14:00 Note to Teams Post-qualifying interview procedures will remain as the previous Event, the top three drivers will again be interviewed as soon as they get out of their cars on the track. Should either of your drivers be among the top three at the end of qualifying we would like to ask for your co-operation in following the procedure below : - If they take the chequered flag at the end of Q3, the fastest three drivers should complete the lap and then proceed to the grid and stop in front of the usual 1-2-3 boards which will have been placed close to pole position. The interviewer will be David Coulthard. - Other than the team mechanics (with cooling fans if necessary), officials and accredited television crews and photographers, no one else will be allowed on the grid at this time (so please no driver physios nor team PR personnel). - Once out of their cars the interviews will take place on the grid, the interviewers will be Paul di Resta. At the same time team mechanics should push the cars to the parc fermé in the weighing area. - If one of the top three drivers is in the pit lane at the end of the session the team should ensure that he goes directly to the grid once the other drivers have arrived there. - At the end of the live interviews the drivers will walk through the pit wall door towards the parc fermé and then be led to the backdrop for the AfRS photo opportunity. -

Your Essential Guide 2018
YOUR ESSENTIAL GUIDE 2018 Contents Welcome 05 Useful local information 24 Equipment check-list and must-take items 06 Travelling by tram 25 Before you leave and driving in France 07 Bars and restaurants in Le Mans 26 Routes to the circuit and the channel ports 08 Dailysportscar 27 On-circuit Events 14 Where to watch the action 29 Motorsport Photography - Jessops Academy 15 Teams and cars entry list 30 2018 Race week schedule 16 Le Mans 2018 Challengers 32 Friday at Le Mans 16 Le Mans 24 Previous Winners 34 More than just Radio Le Mans 19 Emergency Telephone Numbers 38 Grandstands Map 20 Travel Destinations on Facebook and Twitter 39 Points of Interest Map 21 Battle of the Brands 40 Circuit and Campsites Map 22 WEC Silverstone Offer 43 4 Travel Destinations - Le Mans 2018 Welcome Welcome Welcome and thank you for booking with Travel Destinations. For those customers that are joining us at either our private campsite at Porsche Curves, our Event Tents or Travel Destinations is the UK’s leading tour operator for our Flexotel Village at Antares Sud, you will receive Le Mans, including the Le Mans 24 Hours & the Le Mans important information & joining instructions for your Classic. We are committed to provide you, our highly-valued chosen area separately. customers, with the very best customer service and peace of mind with the government backed financial security for The Travel Destinations team will be at the circuit your booking with our ABTA, ATOL and AITO membership. throughout race week, so should you see any of us on your travels, please do come and introduce yourself, As always, we have staff onsite at the circuit and we are as we will be delighted to see you. -
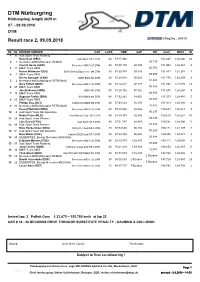
List & Label Report
DTM Nürburgring Nürburgring, length 3629 m 07. - 09.09.2018 DTM Result race 2, 09.09.2018 -Reg.No.: 254/18 Rk No ENTRANT/DRIVER CAR LAPS TIME GAP INT km/h BEST IN 1 33 Audi Sport Team Rosberg René Rast (DEU) Audi Sport RS 5 DTM 40 57:17.440 152.025 1:24.246 23 2 3 Mercedes-AMG Motorsport REMUS 02.739 Paul Di Resta (GBR) Mercedes-AMG C 63 DTM 40 57:20.179 02.739 151.904 1:24.241 4 3 11 BMW Team RMG 00.700 Marco Wittmann (DEU) BMW Driving Experience M4 DTM 40 57:20.879 03.439 151.873 1:24.278 4 4 7 BMW Team RBM 02.204 Bruno Spengler (CAN) BMW Bank M4 DTM 40 57:23.083 05.643 151.776 1:24.259 4 5 2 Mercedes-AMG Motorsport PETRONAS 01.534 Gary Paffett (GBR) Mercedes-AMG C 63 DTM 40 57:24.617 07.177 151.708 1:23.875 23 6 47 BMW Team RBM 00.685 Joel Eriksson (SWE) BMW M4 DTM 40 57:25.302 07.862 151.678 1:24.244 4 7 15 BMW Team RMG 06.940 Augusto Farfus (BRA) Shell BMW M4 DTM 40 57:32.242 14.802 151.373 1:24.480 5 8 25 BMW Team RMR 01.372 Philipp Eng (AUT) SAMSUNG BMW M4 DTM 40 57:33.614 16.174 151.313 1:24.188 4 9 94 Mercedes-AMG Motorsport PETRONAS 14.432 Pascal Wehrlein (DEU) Mercedes-AMG C 63 DTM 40 57:48.046 30.606 150.683 1:24.321 4 10 4 Audi Sport Team Abt Sportsline 00.297 Robin Frijns (NLD) Aral Ultimate Audi RS 5 DTM 40 57:48.343 30.903 150.670 1:24.257 30 11 28 Audi Sport Team Phoenix 03.444 Loic Duval (FRA) Audi Sport RS 5 DTM 40 57:51.787 34.347 150.521 1:24.546 5 12 99 Audi Sport Team Phoenix 01.838 Mike Rockenfeller (DEU) Schaeffler Audi RS 5 DTM 40 57:53.625 36.185 150.441 1:24.139 4 13 51 Audi Sport Team Abt Sportsline 00.260 -

FIA World Endurance Championship Round 4 - 24 Hours of Le Mans 2021 August 13Th to 22Th
Posted at: 22:23 Doc No.: 82 FIA World Endurance Championship Round 4 - 24 Hours of Le Mans 2021 August 13th to 22th Decision No. 94 - 104 From: The Stewards TOYOTA GAZOO RACING, UNITED AUTOSPORTS, PORSCHE GT TEAM, Date: 19 August 2021 To: TEAM PROJECT 1, TEAM WRT, CORVETTE Time (decision): 21:44 h RACING, GR RACING, GLICKENHAUS RACING, INCEPTION RACING The Stewards, having received a report from the FIA Race Director, have considered the following matter, determine a breach of the regulations has been committed by the competitor named below and impose the penalty referred to. Session: Qualifying Hyperpole Fact: Left the track at the place specified as reported by the duly appointed judge of fact and/or by video Offence: Appendix L, chap. IV, art. 2c of International Sporting Code Decision: Deletion of lap times Reason: Constantly abuse of track limits Competitors are reminded that, in accordance with Art. 12.3.4 of the FIA International Sporting Code and Art. 16.2.6 of 24 Hours of Le Mans Supplementary Regulations this decision is not subject to appeal. Lap of car when Dec. Car Driver Competitor infringement occurred and lap time deleted 94 91 Gianmaria Bruni PORSCHE GT TEAM 1 95 56 Matteo Cairoli TEAM PROJECT 1 2 96 23 Paul Di Resta UNITED AUTOSPORTS 2, 6 97 64 Nicholas Tandy CORVETTE RACING 4 98 71 Ben Barnicoat INCEPTION RACING 4 99 7 Kamui Kobayashi TOYOTA GAZOO RACING 6 100 709 Romain Dumas GLICKENHAUS RACING 6, 7, 8 101 41 Louis Delétraz TEAM WRT 6 102 91 Gianmaria Bruni PORSCHE GT TEAM 5 103 32 Nicolas Jamin UNITED AUTOSPORTS 6 104 86 Tom Gamble GR RACING 8 Jean-Francois Rikki Chris Michael Tim Yves VEROUX DY-LIACCO GEFFROY SCHWÄGERL MAYER BACQUELAINE FIA Steward FIA Steward ASN Steward FIA Steward FIA Steward FIA Steward (Chairman).