TPC NTC/PTC Thermistors Contents NTC/PTC Thermistors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The NTC Thermistors This Is a Negative Temperature Coeffi Cient Resistor Whose Resistance Changes As Ambient Temperature Changes
NTC Thermistors The NTC Thermistors This is a Negative Temperature Coeffi cient Resistor whose resistance changes as ambient temperature changes. Therm- istor comprises 2 or 4 kinds of metal oxides of iron, nickel, cobalt, manganese and copper, being shaped and sintered at high temperature (1200 to 1500 °C) ■ Features ■ Recommended Applications ● Temperature Coeffi cient of Resistance is negative and ● For temperature measurement or temperature detection : extremely large thermometer, temperature controller ● Various kinds of types especially smaller ones are ● For temperature compensation : transistor circuit, available. measuring instruments ● Resistance values are available from 22 Ω to 470 kΩ ■ Physical Characteristics of NTC Thermistors Thermistor is a resistor sensitive to temperature utilizing Fig. 1 the large temperature-coefficient of metal oxide semi- conductor. And its temperature dependency of resistance 1000 value is indicated by the following equation: 1 1 100 R=R0 exp B .................................... (1) ( )[ ( T T 0 )[ ] 10 T0: Standard Temperature 298.15 K(25 °C) 25 0 0 R: Resistance at T K /R 1 T B: Thermistor Constant (K) R B=1000 So called Temperature Coefficient (a) is generally 2000 3000 indicated as follows: 0.1 4000 B 5000 a= .................................................................... (2) T2 0.01 6000 But a is not adequate for use as a constant, because a 0.001 change by temperature is considerably large, so B Value –40 –20 0 20 40 60 80 100 120 140 is used as a coeffi cient of thermistor. T (˚C) ■ Major Characteristics of NTC Thermistors The relation between resistance and temperature of a Fig. 2 thermistor is linear as shown in Fig. -

NTC Thermistors Circuit Protection Components
Product catalog Product NTC thermistors Circuit protection components Cat. No. 129L INDEX 1.Application examples ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 3 2.What are "NTC thermistors"? ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 4 3.Basic specifications ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 4 4.How to choose the right thermistor ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 5 5.How to choose the right power thermistor ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 5 Type desription SEMITEC series name Temperature range ■ Micro thin film thermistor FT thermistor (- 40 ℃ to 250 ℃ ) ‥‥‥‥‥‥‥ 6 - 7 ■ Micro thin film type sensor probe Fµ thermistor (- 10 ℃ to 70 ℃ ) ‥‥‥‥‥‥‥ 8 ■ Thin film thermistor JT thermistor (- 40 ℃ to 100 ℃ ) ‥‥‥‥‥‥‥ 9 ■ Very high accuracy thermistor AP thermistor (- 60 ℃ to 150 ℃ ) ‥‥‥‥‥‥‥ 10 - 11 ■ High accuracy thermistor AT thermistor (- 50 ℃ to 110 ℃ ) ‥‥‥‥‥‥‥ 12 - 13 ■ High sensitivity thermistor ET thermistor (- 50 ℃ to 125 ℃ ) ‥‥‥‥‥‥‥ 14 - 15 ■ SMD type thermistor KT thermistor (- 40 ℃ to 125 ℃ ) ‥‥‥‥‥‥‥ 16 - 17 ■ High temperature thermistor NT thermistor (- 50 ℃ to 300 ℃ ) ‥‥‥‥‥‥‥ 18 CT thermistor (- 50 ℃ to 250 ℃ ) ‥‥‥‥‥‥‥ 19 ■ Non-contact (IR) temperature sensor NC sensor (- 10 ℃ to 150 ℃ ) ‥‥‥‥‥‥‥ 20 Thermopile (- 50 ℃ to 200 ℃ ) ‥‥‥‥‥‥‥ 21 ■ Current regulating diode CRD (- 40 ℃ to 150 ℃ ) ‥‥‥‥‥‥‥ 22 - 23 ■ Voltage regulating diode VRD (- 40 ℃ to 150 ℃ ) ‥‥‥‥‥‥‥ 24 - 25 ■ Inrush current limiter Power thermistor (- 50 ℃ to 200 ℃ ) ‥‥‥‥‥‥‥ 26 - 27 High accuracy Fμ Thermistor AP Thermistor FT Thermistor ET Thermistor JT Thermistor AT Thermistor SMD type KT Thermistor NT Thermistor -

Thermometrics NTC Diode Thermistors
NTC Diode Thermometrics Thermistors A range of NTC chip thermistors in DO-35 style • Available on axial bandolier to IEC-286-1/ glass package (diode outline) with axial solder- EIA-468A and packet taped to EIA RS-481 for coated copper-clad steel wires. MELF. • Designed for accurate temperature • Also available loose-packed with axial, radial measurement, control and compensation and SMD wire forms • Tight tolerances on resistance and B value • Suitable for automotive, telecom (battery packs), HVAC and white goods applications • Operation up to 482°F (250°C) with excellent stability • Temperature sensing for household appliances such as rice cookers, electronic • Glass body provides hermetic seal and ranges, ovens, etc. voltage insulation and excellent stability • Temperature sensing for industrial products • Designed for cost effective solid state sensor such as pharmaceuticals, chemicals, food, etc.components. • Lead-wires metallurgically bonded to thermistor element for improved reliability (Type GE only) • Resistant to corrosive atmospheres and harsh environments Amphenol Advanced Sensors Type DK 0.08 in (2 mm) 0.02 in (0.5 mm) Specifications DK-N maximum nominal Chip thermistor in DO-35 glass package 1.06 in (27 mm) 0.2 in (4.2 mm) minimum maximum Options DK-H • Other resistance values within the ranges shown; e.g. code DKA302*2 for 3000 Ω 0.08 in (2 0.16 in (4 mm) mm) maximum 0.1 in (2.8 mm) Inside radius ±2% at 77°F (25°C) nominal Ø 0.02 in (0.5 mm) nominal 0.05 in (1.2 • Reference temperatures in the range 0°F mm) nominal to 302°F -

Application Note
VISHAY BCCOMPONENTS www.vishay.com Resistive Products Application Note NTC Thermistors APPLICATIONS AUTOMOTIVE APPLICATIONS INDUSTRIAL, TELECOMMUNICATIONS, CONSUMER NTC temperature sensors are widely used in motor vehicles. In switching, measuring and detection systems For example: • Process control • Inlet air-temperature control • Heating and ventilation • Transmission oil temperature control • Air conditioning • Engine temperature control • Fire alarms • Airco systems • Temperature protection in battery management / charging • Airbag electronic systems systems • Temperature detection of laser diode in CD players for • LCD contrast control in flat-panel displays, mobile phones cars and camcorders • Frost sensors • Temperature compensation of quartz oscillator frequency •ABS in, for example, mobile phones • BMS / charge plugs protection • Ink-jet printer head temperature detection • Video and audio equipment DOMESTIC APPLIANCES • LED control circuits NTC temperature sensors are in virtually all equipment in the home where temperature plays a role. This includes: • Fridges and freezers • Cookers and deep-fat fryers • Washing machines and dish washers • Central-heating systems • Air conditioning SELECTION CHART TOL. LEAD OPERATING B RESP. MAX. ON R (± %) DOCUMENT PRODUCT RANGE TEMP. RANGE TOL. TIME Ø OR Ø L NUMBER (°C) (± %) (s) (mm) ON T (± °C) (mm) (mm) Accuracy line APPLICATION NOTE NTCLE203E3 -40 to +125 (1 , 2, 3, 5) % 0.5 to 2.5 1.7 3.4 0.4 38 min. 29048 NTCLE100E3 -40 to +125 (2, 3, 5) % 0.5 to 3.0 1.2 3.8 0.6 17 min. 29049 two-point NTCLE101E3...SB0 -40 to +125 0.5 °C 1.2 3.3 0.6 17 min. 29046 sensors two-point NTCLE203E3...SB0 -55 to +150 0.5 °C 1.7 4.2 0.5 41 29118 sensors SMD versions NTCS0603E3 -40 to +150 (1, 2, 3, 5) % 1 - - - - 29056 NTCS0402E3 -40 to +150 (1, 2, 3, 5) % 3 - - - - 29003 NTCS0805E3 -40 to +150 (1, 2, 3, 5) % 1 - - - - 29044 NTCS….E3…SMT -40 to +125 1 % 1 - - - - 29151 Revision: 27-Jan-2021 1 Document Number: 29053 For technical questions, contact: [email protected] THIS DOCUMENT IS SUBJECT TO CHANGE WITHOUT NOTICE. -

1 Light-Emitting Diode
1 Light-emitting diode parameter n is called the ideality factor and usually 1 < n < 2. The parameter VG0 is called the nominal Light Emitting Diodes (LEDs) are the most efficient bandgap voltage of the semiconductor material. 0 light sources. During recent years, the cheap, powerful The voltage across a physical diode V = V + IdRs and reliable LED light bulbs appeared on the market. has also contribution from a parasitic series resistance This is making a true revolution worldwide, as other Rs which is of the order of 1 Ω. Hint: estimate the electrical lighting tools (e.g. incandescent, halogen and magnitudes in the expression above and simplify your fluorescent) in homes and offices are being replaced with calculations accordingly! LED lighting. In this experiment, we will analyse thermal and elec- 1. Measure and plot the voltage–temperature graph of trical properties of the light emitting diodes. the LED at a constant current (your current should You do not need to estimate any uncertainties, but be small enough so that the voltage drop on Rs can the accuracy of your methods and results is important be neglected). and will be graded. Always draw the measurement setup Find VG0. you use! When appropriate, use graphs for determining required quantities. Find the parameters n and A by making additional measurements and a suitable plot. Equipment: 2 identical circuit boards with a LED, res- istor and a temperature sensor on them; 2 transparent At larger currents, the series resistance Rs becomes bottles, 2 airtight caps, 2 tubes, water, syringe, 3 multi- noticeable. Measure this Rs. -

A Thermistor Is a Type of Resistor Used to Measure Temperature Changes
Name of student:…………………………………….. 7 PHYSICAL CHARACTERISTICS OF THERMISTOR Task: Determine physical characteristics of a thermistor (constants A and B) from five temperature and resistance measurement. Calculate the resistance of the termistor and the temperature coefficient % at 0, 25 oC using the Equations [3] and [5] and the obtained values A and B. The word thermistor is a combination of words “thermal” and “resistor”. A thermistor is a temperature-sensing element composed of sintered semiconductor material which exhibits a large change in resistance proportional to a small change in temperature. Thermistors can be classified into two types: If the resistance increases with increasing temperature, the device is called a positive temperature coefficient (PTC) thermistor, posistor. If the resistance decreases with increasing temperature, the device is called a negative temperature coefficient (NTC) thermistor. PTC thermistors can be used as heating elements in small temperature-controlled ovens. NTC thermistors are used as resistance thermometers in low-temperature measurements of the order of 10 K. NTC thermistors can be used also as inrush- current limiting devices in power supply circuits. They present a higher resistance initially which prevents large currents from flowing at turn-on, and then heat up and become much lower resistance to allow higher current flow during normal operation. These thermistors are usually much larger than measuring type thermistors, and are purpose designed for this application. Thermistors are also commonly -
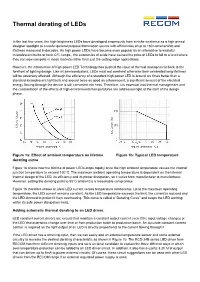
Thermal Derating of Leds
Thermal derating of LEDs In the last few years, the high-brightness LEDs have developed enormously from a niche existence as a high-priced designer spotlight to a useful general purpose illumination source with efficiencies of up to 160 Lumens/Watt and lifetimes measured in decades. As high power LEDs have become more popular as an alternative to wasteful incandescent bulbs or toxic CFL lamps , the economies of scale have caused the price of LEDs to fall to a level where they can now compete in mass markets rather than just the cutting edge applications. However, the introduction of high power LED Technology has pushed the issue of thermal management back to the forefront of lighting design. Like all semiconductors, LEDs must not overheat otherwise their celebrated long lifetimes will be adversely affected. Although the efficiency of a standard high power LED is around six times better than a standard incandescent light bulb and around twice as good as a fluorescent, a significant amount of the electrical energy flowing through the device is still converted into heat. Therefore, it is essential that thermal management and the consideration of the effects of high environmental temperatures are addressed right at the start of the design phase. Figure 1a: Effect of ambient temperature on lifetime Figure 1b: Typical LED temperature derating curve Figure 1a shows how the lifetime of power LEDs drops rapidly once the high ambient temperature causes the internal junction temperature to exceed 130°C. The maximum ambient operating temperature is dependent on the internal thermal design of the LED, its efficiency and its power dissipation, so it varies from manufacturer to manufacturer. -

NTC Thermistors, Application Notes
NTC Thermistors Application notes Date: January 2018 © EPCOS AG 2018. Reproduction, publication and dissemination of this publication, enclosures hereto and the information contained therein without EPCOS' prior express consent is prohibited. EPCOS AG is a TDK Group Company. Application notes 1 Applications utilizing the influence of ambient temperature on resistance (self-heating negligible) 1.1 Temperature measurement The high sensitivity of an NTC thermistor makes it an ideal candidate for temperature sensing ap- plications. These low-cost NTC sensors are normally used for a temperature range of 40 °C to +300 °C. Selection criteria for NTC thermistors are temperature range resistance range measuring accuracy environment (surrounding medium) response time dimensional requirements. One of the circuits suitable for temperature measurement is a Wheatstone bridge with an NTC thermistor used as one bridge leg. Figure 1 Wheatstone bridge circuit With the bridge being balanced, any change in temperature will cause a resistance change in the thermistor and a significant current will flow through the ammeter. It is also possible to use a vari- able resistor R3 and to derive the temperature from its resistance value (in balanced condition). An example of a circuit including an NTC thermistor and microcontroller is given in figure 2. Figure 2 Practical application for a circuit with NTC thermistor and microcontroller Please read Important notes Page 2 of 16 and Cautions and warnings. Application notes 1.2 Linearizing the R/T characteristic NTC thermistors exhibit a distinctly non-linear R/T characteristic. If a fairly linear curve is required for measurements over a (wide) temperature range, e.g. -

Using the NTC Inside a Power Electronic Module Considerations Regarding Temperature Measurement
Application Note, V1.0, Nov. 2009 AN2009 -10 Using the NTC inside a power electronic module Considerations regarding temperature measurement IMM INP LP Edition 2010-01-13 Published by Infineon Technologies AG 59568 Warstein, Germany © Infineon Technologies AG 2010. All Rights Reserved. LEGAL DISCLAIMER THE INFORMATION GIVEN IN THIS APPLICATION NOTE IS GIVEN AS A HINT FOR THE IMPLEMENTATION OF THE INFINEON TECHNOLOGIES COMPONENT ONLY AND SHALL NOT BE REGARDED AS ANY DESCRIPTION OR WARRANTY OF A CERTAIN FUNCTIONALITY, CONDITION OR QUALITY OF THE INFINEON TECHNOLOGIES COMPONENT. THE RECIPIENT OF THIS APPLICATION NOTE MUST VERIFY ANY FUNCTION DESCRIBED HEREIN IN THE REAL APPLICATION. INFINEON TECHNOLOGIES HEREBY DISCLAIMS ANY AND ALL WARRANTIES AND LIABILITIES OF ANY KIND (INCLUDING WITHOUT LIMITATION WARRANTIES OF NON-INFRINGEMENT OF INTELLECTUAL PROPERTY RIGHTS OF ANY THIRD PARTY) WITH RESPECT TO ANY AND ALL INFORMATION GIVEN IN THIS APPLICATION NOTE. Information For further information on technology, delivery terms and conditions and prices please contact your nearest Infineon Technologies Office ( www.infineon.com ). Warnings Due to technical requirements components may contain dangerous substances. For information on the types in question please contact your nearest Infineon Technologies Office. Infineon Technologies Components may only be used in life-support devices or systems with the express written approval of Infineon Technologies, if a failure of such components can reasonably be expected to cause the failure of that life-support device or system, or to affect the safety or effectiveness of that device or system. Life support devices or systems are intended to be implanted in the human body, or to support and/or maintain and sustain and/or protect human life. -

Dictionary: Know Your Resistors
TN-009 Tech Note Dictionary: Know Your Resistors Adhesion: The ability of dissimilar metals or particles to cling together as a joint is referred to as adhesion. Adhesion in thick film is created by either a chemical (oxide bonded) or mechanical (Frit) bonds. Peel test can be used to measure adhesion between lead and substrate and dielectric. Alpha coefficient: In a thermally sensitive resistor or Thermistor applications, the alpha (α) coefficient is a material characteristics which defines the percentage resistance change per degree centigrade. It is also known as the temperature coefficient and it’s calculated by the following relationship; 1 dR α = /RT x /dT Where RT is the resistance of the component at the relevant temperature in (°C), dR/dT is the gradient of the R vs. T curve at that temperature point and alpha is expressed in (%/°C) Annealing: Annealing is a heat process whereby a material (metal or glass) is heated to a specific temperature (annealed point) and then allowed to cool slowly in order to maintain ductility and prevent crack and internal stress. Aspect Ratio (AR): The ratio of resistor length to resistor width is the aspect ratio. It’s also known as the number of squares. Amplitude Balance: The maximum deviation or difference in amplitude between the output ports of a power divider across the operating frequency range. It’s measured in dB AQL (Acceptable Quality Limit): This is a statistical measurement of the maximum number of defective goods considered acceptable in a particular sample size or lot. Attenuation: The loss of signal (Power or Amplitude level) in transmission through the use of attenuators or a filter; It’s measured in decibels (dB). -

Thermal Protection of IGBT Modules for HEV and EV Traction Inverters Reference Design
TI Designs Thermal Protection of IGBT Modules for HEV and EV Traction Inverters Reference Design Description Features This reference design is a temperature sensing • Designed for Traction Inverters With Rated Current solution for IGBT thermal protection in hybrid electric up to 300 A and DC Bus Voltage up to 400 V vehicle and electric vehicle (HEV and EV) traction- • An IGBT Half-Bridge Evaluation Platform That inverter systems. The solution monitors the IGBT Includes Gate Driver, Isolation, NTC Signal temperature through the NTC thermistor that is Conditioning Circuit, Interface to MCU, and Load integrated inside of the IGBT module and provides Resistor thermal shutdown to the IGBT gate drivers once the NTC thermistor temperature rises above the • Push-Pull Current Boost at Gate Driver That programmed threshold. The design includes the IGBT Enables 10-A Source and 10-A Sink Peak Gate isolated gate drivers, NTC signal conditioning, I2C Currents interface and isolation, and a load resistor that enables • One Multichannel ADC and one Isolation IC for the system to run independently under high power Conditioning Multi NTCs in Inverter System ratings. • 8-kV Reinforced Isolation and CMTI Greater Than 50 kV/µs Resources Applications TIDA-00794 Design Folder ISO5852S Product Folder • HEV and EV Traction Inverters ADS1015-Q1 Product Folder • Variable Speed Motor Drives LM5160-Q1 Product Folder • Solar Inverters TPS57140-Q1 Product Folder MSP-EXP430F5529LP Tools Folder ASK Our E2E Experts 12 V to 5 V Step-down DC-DC Converter Isolated Fly-BuckTM -

Ntc Thermistors
NTC THERMISTORS WHAT IS A THERMISTOR • Bare Beads • Glass Coated Beads A thermistor is an electronic component that • Ruggedized Beads exhibits a large change in resistance with a change • Miniature Glass Probes in its body temperature. The word “thermistor” is • Glass Probes actually a contraction of the words “thermal resistor”. • Glass Rods The thermistors that we shall describe herein are • Bead-in-Glass Enclosures ceramic semiconductors and have either large positive temperature coefficient of resistance (PTC The second group of thermistors have metallized devices) or large negative temperature coefficient of surface contacts. All of these types are available resistance (NTC devices). Both types of thermistors with radial or axial leads as well as without leads for (PTC and NTC) have definite features and surface mounting or mounting by means of spring advantages which make them ideal for certain contacts. sensor applications. Metallized surface contact thermistors include NTC THERMISTORS the following: The NTC thermistors which are discussed herein are composed of metal oxides. The most commonly • Disks used oxides are those of manganese, nickel, cobalt, • Chips (Wafers) iron, copper and titanium. The fabrication of • Surface Mounts commercial NTC thermistors uses basic ceramics • Flakes technology and continues today much as it has for • Rods decades. In the basic process, a mixture of two or • Washers more metal oxide powders are combined with suitable binders, are formed to a desired geometry, NTC thermistors are available in a wide variety of dried, and sintered at an elevated temperature. By configurations and protective coatings to suit almost varying the types of oxides used, their relative any application.