DOCSLIB.ORG

Physical Vs. Numerical Dispersion in Nonhydrostatic Ocean Modeling ⇑ Sean Vitousek , Oliver B

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Physical Vs. Numerical Dispersion in Nonhydrostatic Ocean Modeling ⇑ Sean Vitousek , Oliver B Ocean Modelling 40 (2011) 72–86 Contents lists available at ScienceDirect Ocean Modelling journal homepage: www.elsevier.com/locate/ocemod Physical vs. numerical dispersion in nonhydrostatic ocean modeling ⇑ Sean Vitousek , Oliver B. Fringer Environmental Fluid Mechanics Laboratory, Stanford University, Stanford, CA 94305, United States article info abstract Article history: Many large-scale simulations of internal waves are computed with ocean models solving the primitive Received 11 September 2010 (hydrostatic) equations. Under certain circumstances, however, internal waves can represent a dynamical Received in revised form 29 May 2011 balance between nonlinearity and nonhydrostasy (dispersion), and thus may require computationally Accepted 1 July 2011 expensive nonhydrostatic simulations to be well-resolved. Most discretizations of the primitive equa- Available online 14 July 2011 tions are second-order accurate, inducing numerical dispersion generated from odd-order terms in the truncation error (3rd-order derivatives and higher). This numerical dispersion mimics physical dispersion Keywords: due to nonhydrostasy. In this paper, we determine the numerical dispersion coefficient associated with Dispersion common discretizations of the primitive equations. We compare this coefficient to the physical disper- Nonhydrostatic effects Internal waves sion coefficient from the Boussinesq equations or KdV equation. The results show that, to lowest order, 2 Ocean modeling the ratio of numerical to physical dispersion is C = Kk , where K is an O(1) constant dependent on the dis- Grid resolution requirements cretization of the governing equations and k is the grid leptic ratio, k Dx/h1, where Dx is the horizontal Leptic ratio grid spacing and h1 is the depth of the internal interface. In addition to deriving this relationship, we ver- Lepticity ify that it indeed holds in a nonhydrostatic ocean model (SUNTANS). To ensure relative dominance of physical over numerical effects, simulations require C 1. Based on this condition, the horizontal grid spacing required for proper resolution of nonhydrostatic effects is k < O(1) or Dx < h1. When this condi- tion is not satisfied, numerical dispersion overwhelms physical dispersion, and modeled internal waves exist with a dynamical balance between nonlinearity and numerical dispersion. Satisfaction of this con- dition may be a significant additional resolution requirement beyond the current state-of-the-art in ocean modeling. Published by Elsevier Ltd. 1. Introduction and de-Vries, 1895). These equations represent the depth-averaged conservation of mass and momentum and include dispersive Dispersion, a characteristic of nonlinear or nonhydrostatic effects due to nonhydrostasy by retaining the lowest-order effects waves, occurs when the wave speed is a non-constant function of of integrating the nonhydrostatic pressure over the depth. The KdV the wave amplitude or wave frequency (or similarly wavelength) equation reduces conservation of mass and momentum to a single (Whitham, 1974). Distinction is sometimes made between these equation which is valid only for unidirectional wave propagation. two types of dispersion, namely amplitude dispersion and In this paper, we rely heavily on the Boussinesq equations and frequency dispersion, respectively (LeBlond and Mysak, 1978). KdV equation as models that faithfully represent nonlinear and The two are synonymous with nonlinearity and nonhydrostasy in nonhydrostatic behavior in more complicated natural systems, in studies of gravity waves, and hence are typically called nonlinear- this case, oceanic internal gravity waves. ity and dispersion. Many researchers have relied on weakly nonlinear, weakly non- Interesting wave phenomena exist when both nonlinearity and hydrostatic KdV theory to understand both qualitative and quanti- dispersion occur together and with approximately equal magni- tative details of internal waves (Helfrich and Melville, 2006). tude. Under such circumstances, nonlinear steepening balances Internal wave dynamics have been examined using the KdV dispersive spreading, and propagating waves of constant form framework which shows good comparison of internal wave pro- known as ‘‘solitary’’ waves are possible (Korteweg and de-Vries, files with the analytical result from the KdV equation (Liu et al., 1895). The most common equations satisfying the balanced motion 1998; Stanton and Ostrovsky, 1998; Duda et al., 2004; Warn- include the Boussinesq equations (Boussinesq, 1871, 1872; Pere- Varnas et al., 2010). Developments extending KdV theory to fully grine, 1967) and the Korteweg–de Vries (KdV) equation (Korteweg nonlinear dynamics have made significant contributions to the literature, a complete list of which is given in Helfrich and Melville ⇑ Corresponding author. (2006). However, weakly nonlinear, weakly nonhydrostatic scaling E-mail addresses: [email protected] (S. Vitousek), [email protected] (O.B. of many internal wave problems justifies use of traditional KdV Fringer). theory. 1463-5003/$ - see front matter Published by Elsevier Ltd. doi:10.1016/j.ocemod.2011.07.002 S. Vitousek, O.B. Fringer / Ocean Modelling 40 (2011) 72–86 73 Many oceanic internal waves are long relative to the depth and ing equations. Often second-order central differences are used, hence are nearly hydrostatic. Therefore, modeling waves of such implying that the dominant numerical dispersion coefficient is pro- scale with a hydrostatic model may be appropriate (Kantha and portional to the horizontal grid spacing squared. In this paper, we Clayson, 2000). In many other cases, near continental shelves and determine the numerical dispersion coefficient from the modified ocean ridges, internal waves can be highly nonlinear and nonhy- equivalent partial differential equation given from a particular dis- drostatic, often appearing as rank-ordered solitary-like wave trains cretization (Hirt, 1968). Such analyses would be of limited use with- (Hunkins and Fliegel, 1973; Apel et al., 1985; Liu et al., 1998; Scotti out, as a point of comparison, the physical dispersion coefficient. For and Pineda, 2004). Thus, simulations of internal waves may require internal waves, as mentioned previously, this is provided by the fully nonhydrostatic models (such as MITgcm (Marshall et al., Boussinesq equations or the KdV equation. Realistic nonhydrostatic 1997), SUNTANS (Fringer et al., 2006), nonhydrostatic ROMS simulations require that the physical dispersion is much larger than (Kanarska et al., 2007)). The drawback of fully nonhydrostatic the numerical dispersion. Because the physical dispersion for a gi- models is the computational cost associated with solving a 3-D ven problem is typically fixed, the problem of minimizing numerical elliptic equation for the nonhydrostatic pressure, which may re- dispersion in nonhydrostatic ocean models reduces to the problem quire an order of magnitude increase in computational time (Frin- of providing adequate horizontal resolution. As we will show, this ger et al., 2006). The prohibitive computational cost requirement as adequate horizontal resolution is Dx < h1 where Dx is the horizontal well as the nearly hydrostatic scales make primitive (hydrostatic) grid spacing and h1 is the depth of the internal interface. ocean models the preferred method for simulating internal waves The remainder of this paper is divided into four sections. Sec- in the ocean. Although not as computationally expensive, the prim- tion 2 presents the governing equations for modeling dynamics itive equations do not resolve physical dispersion resulting from of internal waves used in our analysis and derives the ratio of nonhydrostatic effects. However, this may not be a problem when numerical to physical dispersion and associated resolution require- physical dispersion is negligible. An excellent discussion concern- ments of a model. Section 3 presents numerical simulations of the ing the application of hydrostatic models to the problem of simu- KdV equation and the fully nonhydrostatic ocean model SUNTANS lating internal waves is presented in Hodges et al. (2006). They and illustrates how both models are prone to numerical dispersion. propose that future use of primitive ocean models is justified due Finally, Sections 4 and 5 present the discussion and conclusions of to the clear hydrostatic scaling of most problems of interest. How- the methods in this paper, respectively. ever, they also point out issues that modelers must contend with when simulating processes which include internal waves with 2. Governing equations hydrostatic models. As we will show, it is not only the lack of phys- ical dispersion that adversely influences model results of internal We begin with the nondimensional two-layer Boussinesq equa- waves, but the presence of numerical dispersion. tions representing the weakly nonlinear and weakly nonhydrostat- The concept of numerical dispersion is not particularly new. ic motion of the two-layer system depicted in Fig. 1. In this paper, Long has it been known that even if the governing equations are we indicate nondimensional quantities with a ⁄. Following Lynett nondispersive, their discrete model may be (artificially) dispersive and Liu (2002), the governing nondimensional momentum and (Trefethen, 1982). In early work, some authors referred to this as continuity equations in one horizontal dimension which retain ‘‘spurious dispersion’’ (Vichnevetsky, 1980; Vichnevetsky and Bow- the first-order nonlinear and nonhydrostatic effects are given by les, 1982). Numerical
Load more

Recommended publications
  • Dispersion of Tsunamis: Does It Really Matter? and Physics and Physics Discussions Open Access Open Access S
    EGU Journal Logos (RGB) Open Access Open Access Open Access Advances in Annales Nonlinear Processes Geosciences Geophysicae in Geophysics Open Access Open Access Nat. Hazards Earth Syst. Sci., 13, 1507–1526, 2013 Natural Hazards Natural Hazards www.nat-hazards-earth-syst-sci.net/13/1507/2013/ doi:10.5194/nhess-13-1507-2013 and Earth System and Earth System © Author(s) 2013. CC Attribution 3.0 License. Sciences Sciences Discussions Open Access Open Access Atmospheric Atmospheric Chemistry Chemistry Dispersion of tsunamis: does it really matter? and Physics and Physics Discussions Open Access Open Access S. Glimsdal1,2,3, G. K. Pedersen1,3, C. B. Harbitz1,2,3, and F. Løvholt1,2,3 Atmospheric Atmospheric 1International Centre for Geohazards (ICG), Sognsveien 72, Oslo, Norway Measurement Measurement 2Norwegian Geotechnical Institute, Sognsveien 72, Oslo, Norway 3University of Oslo, Blindern, Oslo, Norway Techniques Techniques Discussions Open Access Correspondence to: S. Glimsdal ([email protected]) Open Access Received: 30 November 2012 – Published in Nat. Hazards Earth Syst. Sci. Discuss.: – Biogeosciences Biogeosciences Revised: 5 April 2013 – Accepted: 24 April 2013 – Published: 18 June 2013 Discussions Open Access Abstract. This article focuses on the effect of dispersion in 1 Introduction Open Access the field of tsunami modeling. Frequency dispersion in the Climate linear long-wave limit is first briefly discussed from a the- Climate Most tsunami modelers rely on the shallow-water equations oretical point of view. A single parameter, denoted as “dis- of the Past for predictions of propagationof and the run-up. Past Some groups, on persion time”, for the integrated effect of frequency dis- Discussions the other hand, insist on applying dispersive wave models, persion is identified.
    [Show full text]
  • Waves and Weather
    Waves and Weather 1. Where do waves come from? 2. What storms produce good surfing waves? 3. Where do these storms frequently form? 4. Where are the good areas for receiving swells? Where do waves come from? ==> Wind! Any two fluids (with different density) moving at different speeds can produce waves. In our case, air is one fluid and the water is the other. • Start with perfectly glassy conditions (no waves) and no wind. • As wind starts, will first get very small capillary waves (ripples). • Once ripples form, now wind can push against the surface and waves can grow faster. Within Wave Source Region: - all wavelengths and heights mixed together - looks like washing machine ("Victory at Sea") But this is what we want our surfing waves to look like: How do we get from this To this ???? DISPERSION !! In deep water, wave speed (celerity) c= gT/2π Long period waves travel faster. Short period waves travel slower Waves begin to separate as they move away from generation area ===> This is Dispersion How Big Will the Waves Get? Height and Period of waves depends primarily on: - Wind speed - Duration (how long the wind blows over the waves) - Fetch (distance that wind blows over the waves) "SMB" Tables How Big Will the Waves Get? Assume Duration = 24 hours Fetch Length = 500 miles Significant Significant Wind Speed Wave Height Wave Period 10 mph 2 ft 3.5 sec 20 mph 6 ft 5.5 sec 30 mph 12 ft 7.5 sec 40 mph 19 ft 10.0 sec 50 mph 27 ft 11.5 sec 60 mph 35 ft 13.0 sec Wave height will decay as waves move away from source region!!! Map of Mean Wind
    [Show full text]
  • Basin Scale Tsunami Propagation Modeling Using Boussinesq Models: Parallel Implementation in Spherical Coordinates
    WCCE – ECCE – TCCE Joint Conference: EARTHQUAKE & TSUNAMI BASIN SCALE TSUNAMI PROPAGATION MODELING USING BOUSSINESQ MODELS: PARALLEL IMPLEMENTATION IN SPHERICAL COORDINATES J. T. Kirby1, N. Pophet2, F. Shi1, S. T. Grilli3 ABSTRACT We derive weakly nonlinear, weakly dispersive model equations for propagation of surface gravity waves in a shallow, homogeneous ocean of variable depth on the surface of a rotating sphere. A numerical scheme is developed based on the staggered-grid finite difference formulation of Shi et al (2001). The model is implemented using the domain decomposition technique in conjunction with the message passing interface (MPI). The efficiency tests show a nearly linear speedup on a Linux cluster. Relative importance of frequency dispersion and Coriolis force is evaluated in both the scaling analysis and the numerical simulation of an idealized case on a sphere. 1 INTRODUCTION The conventional models in the global-scale tsunami modeling are based on the shallow water equations and neglect frequency dispersion effects in wave propagation. Recent studies on tsunami modeling revealed that such tsunami models may not be satisfactory in predicting tsunamis caused by nonseismic sources (Løvholt et al., 2008). For seismic tsunamis, the frequency dispersion effects in the long distance propagation of tsunami fronts may become significant. The numerical simulations of the 2004 Indian Ocean tsunami by Glimsdal et al. (2006) and Grue et al. (2008) indicated the undular bores may evolve in shallow water, as the phenomenon evidenced in observations (Shuto, 1985). In the simulation for the same tsunami by Grilli et al. (2007), the dispersive effects were quantified by running the dispersive Boussinesq model FUNWAVE (Kirby et al., 1998) and the NSWE solver.
    [Show full text]
  • Shallow Water Waves and Solitary Waves Article Outline Glossary
    Shallow Water Waves and Solitary Waves Willy Hereman Department of Mathematical and Computer Sciences, Colorado School of Mines, Golden, Colorado, USA Article Outline Glossary I. Definition of the Subject II. Introduction{Historical Perspective III. Completely Integrable Shallow Water Wave Equations IV. Shallow Water Wave Equations of Geophysical Fluid Dynamics V. Computation of Solitary Wave Solutions VI. Water Wave Experiments and Observations VII. Future Directions VIII. Bibliography Glossary Deep water A surface wave is said to be in deep water if its wavelength is much shorter than the local water depth. Internal wave A internal wave travels within the interior of a fluid. The maximum velocity and maximum amplitude occur within the fluid or at an internal boundary (interface). Internal waves depend on the density-stratification of the fluid. Shallow water A surface wave is said to be in shallow water if its wavelength is much larger than the local water depth. Shallow water waves Shallow water waves correspond to the flow at the free surface of a body of shallow water under the force of gravity, or to the flow below a horizontal pressure surface in a fluid. Shallow water wave equations Shallow water wave equations are a set of partial differential equations that describe shallow water waves. 1 Solitary wave A solitary wave is a localized gravity wave that maintains its coherence and, hence, its visi- bility through properties of nonlinear hydrodynamics. Solitary waves have finite amplitude and propagate with constant speed and constant shape. Soliton Solitons are solitary waves that have an elastic scattering property: they retain their shape and speed after colliding with each other.
    [Show full text]
  • Dispersion Coefficients for Coastal Regions
    (!1vL- L/0;z7 /- NUREG/CR-3149 PNL-4627 Dispersion Coefficients for Coastal Regions Prepared by B. L. MacRae, R. J. Kaleel, D. L. Shearer/ TRC TRC Environmental Consultants, Inc. Pacific Northwest Laboratory Operated by Battelle Memorial Institute Prepared for U.S. Nuclear Regulatory Commission NOTICE This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, or any of their employees, makes any warranty, expressed or implied, or assumes any legal liability of re ­ sponsibility for any third party's use, or the results of such use, of any information, apparatus, product or process disclosed in this report, or represents that its use by such third party would not infringe privately owned rights. Availability of Reference Materials Cited in NRC Publications Most documents cited in NRC publications will be available from one of the following sources: 1. The NRC Public Document Room, 1717 H Street, N.W. Washington, DC 20555 2 The NRC/GPO Sales Program, U.S. Nuclear Regulatory Commission, Washington, DC 20555 3. The National Technical Information Service, Springfield, VA 22161 Although the listing that follows represents the majority of documents cited in NRC publications, it is not intended to be exhaustive. Referenced documents available for inspection and copying for a fee from the NRC Public Docu­ ment Room include NRC correspondence and ir.ternal NRC memoranda; NRC Office of Inspection and Enforcement bulletins, circulars, information not1ces, inspection and investigation notices; licensee Event Reports; vendor reports and correspondence; Commission papers; and applicant and licensee documents and correspondence.
    [Show full text]
  • Solitons Et Dispersion
    Solitons et dispersion Raphaël Côte Table des matières Table des matières i Introduction iii Preamble: Orbital stability of solitons vii Solitons . vii Orbital stability of solitons . ix 1 Multi-solitons 1 1 Construction of multi-solitons . 1 2 Families of multi-solitons . 8 2 Soliton resolution for wave type equations 11 1 Profile decomposition . 12 2 Linear energy outside the light cone . 14 3 The nonlinear wave equation in dimension 3 . 17 4 Equivariant wave maps to the sphere S2 ....................... 19 5 Back to the H˙ 1 × L2 critical wave equation: dimension 4 . 23 3 Blowup for the 1D semi linear wave equation 27 1 Blow up and blow up curve . 27 2 Description of the blow up . 28 3 Construction of characteristic points . 33 4 The Zakharov-Kuznetsov flow around solitons 37 1 Liouville theorems . 39 2 Asymptotic stability . 41 3 Multi-solitons . 42 5 Formation of Néel walls 45 1 A two-dimensional model for thin-film micromagnetism . 45 2 Compactness and optimality of Néel walls . 48 3 Formation of static Néel walls . 49 Index 53 Bibliography 55 References presented for the habilitation . 55 General references . 56 i Introduction objet de ce mémoire est de présenter quelques aspects de la dynamique des solutions L’ d’équations aux dérivées partielles dispersives. Le fil conducteur liant les différents travaux exposés ici est l’étude des solitons. Ce sont des ondes progressives ou stationnaires, des objets non linéaires qui préservent leur forme au cours du temps. Elles possèdent des propriétés de rigidité remarquables, et jouent un rôle prééminent dans la description de solutions génériques en temps long.
    [Show full text]
  • Dispersion of Wave Action Abstract Introduction
    Dispersion of Wave Action James M. Buick1 and Tariq S. Durrani2 Abstract The dispersion of particles beneath a random sea, produced by the associated random variations in the Stokes drift is considered. In particular, a sea state described by a Pierson-Moskowitz spectrum is considered and the diffusion rate on and below the surface is examined. For such a random sea the diffusion rate at the surface can be related to the wind speed. This expression is extended to consider dispersion rates below the surface and to relates these to the wind speed. The theory is then applied to study the dispersion of particles denser than water as they fall through a random sea. Introduction An accurate prediction of the dispersion of pollutants in the sea is essential in the planning of contingency exercises and also in risk analysis. Computer models have been developed to simulate the spread of pollutants in the sea but these generally ignore the effects of wave action in dispersing the material which, on a scale of up to a few kilometers, can have a large role to play (Schott et al. 1978, Herterich and Hasselmann 1982). Recent oil spill disasters such as the sinking of the Braer off the Shetland Islands have highlighted the fact that the dispersion of pollutants is highly dependent on the prevailing wave climate. Discharges 'Research Fellow, Signal Processing Division, Department of Electronic and Electrical Engineering, Uni- versity of Strathclyde, Glasgow Gl 1XQ, UK. Present address: Department of Physics and Astronomy, The University of Edinburgh, J.C.M.B., Mayfield Road, Edinburgh EH9 3JZ, U.K, [email protected] 2Professor,Signal Processing Division, Department of Electronic and Electrical Engineering, University of Strathclyde, Glasgow Gl 1XQ, UK 3553 3554 COASTAL ENGINEERING 1998 from chemical and sewage works can also cause pollution.
    [Show full text]
  • Swell and Wave Forecasting
    Lecture 24 Part II Swell and Wave Forecasting 29 Swell and Wave Forecasting • Motivation • Terminology • Wave Formation • Wave Decay • Wave Refraction • Shoaling • Rouge Waves 30 Motivation • In Hawaii, surf is the number one weather-related killer. More lives are lost to surf-related accidents every year in Hawaii than another weather event. • Between 1993 to 1997, 238 ocean drownings occurred and 473 people were hospitalized for ocean-related spine injuries, with 77 directly caused by breaking waves. 31 Going for an Unintended Swim? Lulls: Between sets, lulls in the waves can draw inexperienced people to their deaths. 32 Motivation Surf is the number one weather-related killer in Hawaii. 33 Motivation - Marine Safety Surf's up! Heavy surf on the Columbia River bar tests a Coast Guard vessel approaching the mouth of the Columbia River. 34 Sharks Cove Oahu 35 Giant Waves Peggotty Beach, Massachusetts February 9, 1978 36 Categories of Waves at Sea Wave Type: Restoring Force: Capillary waves Surface Tension Wavelets Surface Tension & Gravity Chop Gravity Swell Gravity Tides Gravity and Earth’s rotation 37 Ocean Waves Terminology Wavelength - L - the horizontal distance from crest to crest. Wave height - the vertical distance from crest to trough. Wave period - the time between one crest and the next crest. Wave frequency - the number of crests passing by a certain point in a certain amount of time. Wave speed - the rate of movement of the wave form. C = L/T 38 Wave Spectra Wave spectra as a function of wave period 39 Open Ocean – Deep Water Waves • Orbits largest at sea sfc.
    [Show full text]
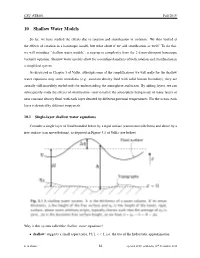
  • 10 Shallow Water Models
    CSU ATS601 Fall 2015 10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification as well? To do this, we will introduce “shallow water models”, a step-up in complexity from the 2-d non-divergent barotropic vorticity equation. Shallow water models allow for a combined analysis of both rotation and stratification in a simplified system. As discussed in Chapter 3 of Vallis, although some of the simplifications we will make for the shallow water equations may seem unrealistic (e.g. constant density fluid with solid bottom boundary), they are 5 Shallowactually still incredibly Water useful tools Models for understanding the atmosphere and ocean. By adding layers, we can So far wesubsequently have studied study the the effects eff ofects stratification due to - rotation and visualize (chapter the atmosphere 3) and being stratification made of many layers (chapter of 4) in isolation.near constant Shallow density water fluid,with models each layer allow denoted for a by combined different potential analysis temperatures. of both For eff theects ocean, in eacha highly simplifiedlayer system. is denoted They by different are very isopycnals. powerful in providing fundamental dynamical insight. 5.1 Introduction,10.1 Single-layer shallow Single water Layer equations[Vallis 3.1] Consider a single layer of fluid bounded below by a rigid surface and above by a free surface, Consider a single layer of fluid bounded below by a rigid surface (cannot move/deform) and above by a as depicted below (taken from Vallis, see figure caption for description of variables).
    [Show full text]
  • On the Dispersion Relation for Compressible Navier-Stokes
    On the dispersion relation for compressible Navier-Stokes Equations Saad Benjelloun∗ and Jean-Michel Ghidaglia∗,§ ∗ Mohammed VI Polytechnic University (UM6P), Modeling Simulation & Data Analytics, Benguerir, Morocco. §Universit´eParis-Saclay, ENS Paris-Saclay, CNRS, Centre Borelli, 91190, Gif-sur-Yvette, France. May 19, 2021 1 Introduction In this paper we revisit the classical sound dispersion and attenuation the- ory due to Stokes [5], 1845, and Kirchhoff [3], 1868, for the propagation of sound in non-ideal fluids. In particular we reformulate the analysis due to Fletcher [2], 1974, showing conditions for which the sound propagates at the isothermal speed of sound. Also we presents asymptotic developments mak- ing precise the physical conditions under which the different dispersion and attenuation formulas apply. The more complex case of two-fluid flow is addressed by Benjelloun and arXiv:2011.06394v2 [math.AP] 18 May 2021 Ghidaglia [1] to which the reader is referred. In [1], it is shown that analytical expressions for the speed of sound depend heavily on the chosen model. These sound speed expressions are compared with experimental values. The consequences for CFD models are also discussed. 1 2 Dispersion relations for a single conductive and viscous fluid In Table 1 below we first give the main notations that are used in this paper. Symbol Quantity Symbol Quantity ρ Density T Temperature µ Dynamic viscosity λ Thermal conductivity c Adiabatic speed of sound cT Isothermal speed of sound Cv Isochoric heat capacity Cp Isobaric heat capacity γ Ratio Cp/Cv Γ Gr¨uneisen parameter Pr Prandtl number µCp/λ Kn Knudsen number (13) Table 1: Notations for a single fluid model (see (6) and (3)).
    [Show full text]
  • Chapter 42 Coupling Stokes and Cnoidal Wave Theories
    CHAPTER 42 COUPLING STOKES AND CNOIDAL WAVE THEORIES IN A NONLINEAR REFRACTION MODEL Thomas A. Hardy1, A.M. ASCE Nicholas C. Kraus2, M. ASCE ABSTRACT An efficient numerical model is presented for calculating the refraction and shoaling of finite-amplitude waves over an irregular sea bottom. The model uses third-order Stokes wave theory in relatively deep water and second-order cnoidal wave theory in relatively shallow water. It can also be run using combinations of lower-order wave theories, including a pure linear wave mode. The problem of the connection of Stokes and cnoidal theories is investigated, and it is found that the use of second-order rather than first-order cnoidal theory greatly reduces the connection discontinuity. Calculations are compared with physical model measurements of the height and direction of waves passing over an elliptical shoal. The finite-amplitude wave model gives better qualitative and quantitative agreement with the measurements than the linear model. INTRODUCTION Wave transformation models are commonly used in coastal engineering projects to provide nearshore wave height and direction. This information is needed at specified grid locations for input into nearshore circulation and shoreline change numerical models. Often, multiple simulations over a wide geographical area are required. Small-amplitude (linear) wave theory is the basis for almost all wave transformation models presently in engineering use. It is well known that finite-amplitude (nonlinear) wave theories predict greater shoaling and less refraction than does small-amplitude theory, and the nearshore wave properties predicted by nonlinear theories are expected to provide an improved description of real waves transforming in shallow water.
    [Show full text]
  • Tsunamis Steven N
    For Publication in: Encyclopedia of Physical Science and Technology - Academic Press 1 Tsunamis Steven N. Ward Institute of Tectonics, University of California at Santa Cruz I. Tsunami = Killer Wave? period, wavelength, and velocity. Unlike com- II. Characteristics of Tsunamis mon sea waves that evolve from persistent sur- III. Tsunami Generation face winds, most tsunamis spring from sudden IV. Tsunami Propagation shifts of the ocean floor. These sudden shifts can V. Tsunami Shoaling originate from undersea landslides and volca- VI. Tsunami Hazard Estimation noes, but mostly, submarine earthquakes parent VII. Tsunami Forecasting tsunamis. Reflecting this heritage, tsunamis often are called seismic sea waves. Compared with GLOSSARY wind-driven waves, seismic sea waves have pe- dispersive: Characteristic of waves whose velocity riods, wavelengths, and velocities ten or a hun- of propagation depends on wave frequency. The dred times larger. Tsunamis thus have pro- shape of a dispersive wave packet changes as it foundly different propagation characteristics and moves along. shoreline consequences than do their common eigenfunction: Functional shape of the horizontal cousins. and vertical components of wave motion versus depth in the ocean for a specific wave frequency. I. Tsunami = Killer Wave? geometrical spreading: Process of amplitude reduction resulting from the progressive expan- Perhaps influenced by Hollywood movies, some sion of a wave from its source. people equate tsunamis with killer waves. Cer- shoal: Process of waves coming ashore. Shoaling tainly a five-meter high tsunami born from a waves slow, shorten their wavelength, and grow great earthquake is impressive. So too is the fact in height. that a tsunami can propagate thousands of kilo- wavenumber: Wavenumber k equals 2p divided by meters and still pack a punch.
    [Show full text]