View Publication
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

International Students' Guide
B.A. Business Administration with Informatics (BBA) M.A. International Management & Information Systems (IMIS) M.A. International Management & Information Systems-Online (IMIS Online) M.Sc. Systems Engineering & Engineering Management (SEEM) International Students‘ Guide Faculty of Electrical Engineering Checklist Pre-departure ◯ Admission letter ◯ Settlement of visa ◯ All academic certificates and transcripts ◯ Up to date passport ◯ Several recent photographs ◯ Settlement of financial concerns ◯ Accommodation confirmation ◯ Travel insurance ◯ Let the BBA/IMIS/IMIS-Online/SEEM office know about your arrival date ◯ Make sure you know the current COVID-19 regulations for travel, arrival and stay in Germany ◯ Registration for orientation class or Welcome Meeting ◯ Check online for the city map ◯ Check the link www.bahn.com for the airport transfer to your arrival city in Germany Arrival checklist BBA, IMIS, SEEM ◯ German SIM card ◯ Accommodation contract ◯ City registration (Rathaus) ◯ Bank account ◯ Apply for residence permit BBA, IMIS, IMIS Online, SEEM ◯ Health insurance ◯ Enroll at the university To-do‘s at the university ◯ Attend orientation class or Welcome Meeting ◯ Apply for the „chiporello“ (student ID and printing card) in the University Online Portal ◯ Configure your personal computer web browser for the Digital Certificate ◯ Contact BBA/IMIS/IMIS-Online/SEEM office for any further queries Before saying goodbye ◯ Get all the necessary contacts from the university ◯ Return books to the library ◯ Collect your certificates and transcripts ◯ Get recommendation letters (if needed) ◯ Settle your bank account if needed ◯ Ensure all your bills and finances are paid up-to-date ◯ Join our social media group (e.g. LinkedIn, XING) to establish the alumni network Enrolment Steps for BBA/IMIS/SEEM Impressum Herausgeber Der Rektor der Fachhochschule Südwestfalen, Professor Dr. -

The Black Watch Museum and Home Headquarters
No. 102 November 2010 THE RED HACKLE Perth and Kinross is proud to be home to the Black Watch Museum and Home Headquarters Delivering Quality to the Heart of Scotland don’t lOSE YOUR VOICE - REGISTER TO VOTE In order to vote you must be registered as an elector. If you are not on the register your views and opinions will count for nothing at election time. You can and should register to vote if you are not already registered. If you have changed your name, please let us know. Members of HM Forces and their spouses or civil partners can register either by means of a service declaration or choose to be registered as an ordinary elector instead. Remember, 16 and 17 year olds who register are entitled to vote as soon as they turn 18. P.S. Did you know that registering to vote can do more than protect your democratic rights? It can also help you open a bank account or get a mortgage, loan or mobile phone. For information on registering to vote: Phone the Freefone Helpline on 0800 393783 e-mail: [email protected] or write to the Electoral Registration Officer, Moray House, 16-18 Bank Street, Inverness IV1 1QY HAVE YOUR SAY No. 102 42nd 73rd November 2010 THE RED HACKLE The Chronicle of The Black Watch (Royal Highland Regiment), its successor The Black Watch, 3rd Battalion The Royal Regiment of Scotland, The Affiliated Regiments and The Black Watch Association Private Sam Morgan receives his Afghanistan campaign medal during the visit or the Royal Colonel to Balhousie Castle on 1 June 2010. -

Alternative Zur A445 Werl-Hamm Im BVWP 2015 Umsetzen!
Alternative zur A 445 Werl – Hamm im BVWP 2015 umsetzen! BUND meldet Null-Variante und die Nutzung der ausreichend leistungsfähigen und bereits optimierte B 63 an. Stand: 30.9.2013 Das Land meldet den Neubau der A 445 von der AS Werl/Nord - AS Hamm/Rhynern (A 2) an. Der BUND meldet als Alternative eine Null-Variante der A 445 und die Nutzung der ausreichend leistungsfähigen und in den letzten Jahren optimierte B 63 (2+1-Ausbau) an. Erläuterungen: Das Land NRW hat für den BVWP 2015 das folgende Fernstraßenvorhaben angemeldet: A 445 AS Werl/Nord - AS Hamm/Rhynern (A 2) VB PO Länge: 8 km Aus verkehrlicher Sicht gibt es für den geplanten Bau der A445 keinen Bedarf. Eine durch die BI „Stoppt A445“ beauftragte Netzbetrachtung (Download auf www.stoppt-a445.de ) kommt zu dem Ergebnis, dass u.a. aufgrund der seit ca. 8 Jahren stagnierenden Verkehrszahlen auf der der B63 keine Notwendigkeit für den Bau der A445 besteht und diese auch aus überregionalen Netzgesichtspunkten keine Relevanz hat. Ursprünglich war die A445 geplant, um in Verbindung mit der ebenfalls geplanten A46 (inkl. neu zu bauender Brücke über das Ruhrtal) die Autobahnen des östlichen Ruhrgebiets (A1, Kreuz Unna, Kamener Kreuz, A2) zu entlasten. Seit September 2011 ist jedoch ein bedeutender Planungsabschnitt, nämlich die Weiterführung von Menden nach Osten bis Neheim „ruhend“ gestellt. Der Regionalrat Arnsberg fordert zwar diese Weiterführung bis nach Neheim. Die ursprünglich geplante weiträumige Entlastungswirkung der A 46 wurde aber durch den inzwischen erfolgten Ausbau der A 1, des notorischen Engpasses Kamener Kreuz sowie der A 2 und die Aufgabe der Vollendung der Anschlusses der A 46 im Westen bei Hagen entbehrlich gemacht. -

LCSH Section W
W., D. (Fictitious character) William Kerr Scott Lake (N.C.) Waaddah Island (Wash.) USE D. W. (Fictitious character) William Kerr Scott Reservoir (N.C.) BT Islands—Washington (State) W.12 (Military aircraft) BT Reservoirs—North Carolina Waaddah Island (Wash.) USE Hansa Brandenburg W.12 (Military aircraft) W particles USE Waadah Island (Wash.) W.13 (Seaplane) USE W bosons Waag family USE Hansa Brandenburg W.13 (Seaplane) W-platform cars USE Waaga family W.29 (Military aircraft) USE General Motors W-cars Waag River (Slovakia) USE Hansa Brandenburg W.29 (Military aircraft) W. R. Holway Reservoir (Okla.) USE Váh River (Slovakia) W.A. Blount Building (Pensacola, Fla.) UF Chimney Rock Reservoir (Okla.) Waaga family (Not Subd Geog) UF Blount Building (Pensacola, Fla.) Holway Reservoir (Okla.) UF Vaaga family BT Office buildings—Florida BT Lakes—Oklahoma Waag family W Award Reservoirs—Oklahoma Waage family USE Prix W W. R. Motherwell Farmstead National Historic Park Waage family W.B. Umstead State Park (N.C.) (Sask.) USE Waaga family USE William B. Umstead State Park (N.C.) USE Motherwell Homestead National Historic Site Waahi, Lake (N.Z.) W bosons (Sask.) UF Lake Rotongaru (N.Z.) [QC793.5.B62-QC793.5.B629] W. R. Motherwell Stone House (Sask.) Lake Waahi (N.Z.) UF W particles UF Motherwell House (Sask.) Lake Wahi (N.Z.) BT Bosons Motherwell Stone House (Sask.) Rotongaru, Lake (N.Z.) W. Burling Cocks Memorial Race Course at Radnor BT Dwellings—Saskatchewan Wahi, Lake (N.Z.) Hunt (Malvern, Pa.) W.S. Payne Medical Arts Building (Pensacola, Fla.) BT Lakes—New Zealand UF Cocks Memorial Race Course at Radnor Hunt UF Medical Arts Building (Pensacola, Fla.) Waʻahila Ridge (Hawaii) (Malvern, Pa.) Payne Medical Arts Building (Pensacola, Fla.) BT Mountains—Hawaii BT Racetracks (Horse racing)—Pennsylvania BT Office buildings—Florida Waaihoek (KwaZulu-Natal, South Africa) W-cars W star algebras USE Waay Hoek (KwaZulu-Natal, South Africa : USE General Motors W-cars USE C*-algebras Farm) W. -

The Path to the FAIR HANSA FAIR for More Than 600 Years, a Unique Network HANSA of Merchants Existed in Northern Europe
The path to the FAIR HANSA FAIR For more than 600 years, a unique network HANSA of merchants existed in Northern Europe. The cooperation of this consortium of merchants for the promotion of their foreign trade gave rise to an association of cities, to which around 200 coastal and inland cities belonged in the course of time. The Hanseatic League in the Middle Ages These cities were located in an area that today encom- passes seven European countries: from the Dutch Zui- derzee in the west to Baltic Estonia in the east, and from Sweden‘s Visby / Gotland in the north to the Cologne- Erfurt-Wroclaw-Krakow perimeter in the south. From this base, the Hanseatic traders developed a strong economic in uence, which during the 16th century extended from Portugal to Russia and from Scandinavia to Italy, an area that now includes 20 European states. Honest merchants – Fair Trade? Merchants, who often shared family ties to each other, were not always fair to producers and craftsmen. There is ample evidence of routine fraud and young traders in far- ung posts who led dissolute lives. It has also been proven that slave labor was used. ̇ ̆ Trading was conducted with goods that were typically regional, and sometimes with luxury goods: for example, wax and furs from Novgorod, cloth, silver, metal goods, salt, herrings and Chronology: grain from Hanseatic cities such as Lübeck, Münster or Dortmund 12th–14th Century - “Kaufmannshanse”. Establishment of Hanseatic trading posts (Hanseatic kontors) with common privi- leges for Low German merchants 14th–17th Century - “Städtehanse”. Cooperation between the Hanseatic cit- ies to defend their trade privileges and Merchants from di erent cities in di erent enforce common interests, especially at countries formed convoys and partnerships. -

RB 59 FAHRPLAN 2020 / 2021 Ankunft Und Anschlüsse
MONTAG - FREITAG Zug-Nummer 90317 90319 90365 90321 90367 90345 90391 90347 90349 90351 90353 90355 90357 90359 Aufgrund einer Baumaßnahme werden ab dem Dortmund Hbf ab 05:04 06:04 06:34 07:04 07:34 19:04 19:34 20:04 21:04 22:04 23:04 00:04 01:04 02:04 02. Juli 2021 von Montag bis Samstag die Züge Dortmund Signal-Iduna-Park 05:12 06:12 06:42 07:12 07:42 19:12 19:42 20:12 21:12 22:12 23:12 00:12 01:12 02:12 Fahrplanauskünfte Dortmund-Hörde 05:15 06:15 06:46 07:15 07:46 19:15 19:46 20:15 21:15 22:15 23:15 00:15 01:15 02:15 des Zwischentakts (Abfahrt Dortmund Hbf zur Dortmund-Aplerbeck 05:19 06:19 06:50 07:19 07:50 19:19 19:50 20:19 21:19 22:19 23:19 00:19 01:19 02:19 Minute :34) mit abweichenden Fahrtzeiten zwi- Dortmund-Sölde 05:23 06:23 06:53 07:23 07:53 19:23 19:53 20:23 21:23 22:23 23:23 00:23 01:23 02:23 schen Dortmund Hbf - Soest und ohne Halt in Aktuelle Fahrzeiten und Informationen Holzwickede / DO Flughafen 05:27 06:27 06:57 07:27 07:57 19:27 19:57 20:27 21:27 22:27 23:27 00:27 01:27 02:27 Dortmund-Aplerbeck verkehren. stehen Ihnen auf unserer Webseite unter Unna an 05:31 06:31 07:01 07:31 08:01 19:31 20:01 20:31 21:31 22:31 23:31 00:31 01:31 02:32 eurobahn.de/abfahrtsinfos zur Verfügung. -

UF00047649 ( .Pdf )
Digitized with the permission of the FLORIDA DEPARTMENT OF MILITARY AFFAIRS FLORIDA NATIONAL GUARD SOURCE DOCUMENT ADVISORY Digital images were created from printed source documents that, in many cases , were photocopies of original materials held elsewhere. The quality of these copies was often poor. Digital images reflect the poor quality of the source documents. Where possible images have been manipulated to make them as readable as possible. In many cases such manipulation was not possible. Where available, the originals photocopied for publication have been digitized and have been added, separately, to this collection. Searchable text generated from the digital images , subsequently, is also poor. The researcher is advised not to rely solely upon text-search in this collection. RIGHTS & RESTRICTIONS Items collected here were originally published by the Florida National Guard, many as part of its SPECIAL ARCHIVES PUBLICATION series. Contact the Florida National Guard for additional information. The Florida National Guard reserves all rights to content originating with the Guard . DIGITIZATION Titles from the SPECIAL ARCHIVES PUBLICATION series were digitized by the University of Florida in recognition of those serving in Florida's National Guard , many of whom have given their lives in defense of the State and the Nation. FLORIDA DEPARTMENT OF MILITARY AFFAIRS Special Archives Publication Number 136 SUMMARY HISTORIES: WORLDWARII AIRBORNE AND ARMOURED DMSIONS State Arsenal St. Francis Barracks St. Augustine, Florida STATE OF FLORIDA DEPARTMENT OF MILITARY AFFAIRS OFFICE OF THE ADJUTANT GENERAL POST OFFICE BOX 1008 STATE ARSENAL, ST. AUGUSTINE 32085-1008 These Special Archives Publications are produced as a service to Florida communities, historians and any other individuals, historical or geneaological societies and both national and state governmental agencies which find the information contained therein of use or value. -

Information Sheet on Searching for a Flat
Information Sheet on Searching for a Flat Searching for a flat • Through the Internet o www.ebay-kleinanzeigen.de o www.immobilienscout24.de o www.immowelt.de o www.meinestadt-soest.de o www.immonet.de o www.wohnungsboerse.net o www.wg-gesucht.de • Through regional newspapers • Through housing associations Contact by telephone, e-mail or through a box number. Viewing appointment It is especially important • to be punctual • to be polite • to have a well-groomed appearance First impressions matter. Express an interest in the flat and specifically ask: • Who else lives in the block of flats? • Where is the cellar? • Is there a supermarket nearby? • What is the bus service like? • Etc. The more an applicant enquires about details and asks questions, the more s/he will be taken seriously. If you find a flat, the Sozialamt (social security office) or Jobcenter will have to have it assessed for appropriateness. For this purpose the landlord will have to complete and sign a Mietbescheinigung (certificate of tenancy) and this then has to be handed in to the Sozialamt (social security office) or Jobcenter. You can request this form at the Sozialamt (social security office) / Jobcenter. A tenancy agreement may not be concluded until the flat has been approved by the Sozialamt (social security office) / Jobcenter. Housing costs for the municipality of Bad Sassendorf (as at: November 2016) Person/ m² Reasonable costs excluding heating costs, service costs 1 person up to € 329.00 approx. 50m² 2 people up to € 418.50 approx. 65m² 3 people up to € 520.00 approx. -

Und Bahnsteigarbeiten Hamm (Westf) Dortmund Hbf 14.07.2018
Umleitung mit Haltausfällen Gleis- und Bahnsteigarbeiten Hamm (Westf) ◄► Dortmund Hbf 14.07.2018 (0:00) – 10.09.2018 (ca. 4:00) Sehr geehrte Fahrgäste, während der Sommerferien und darüber hinaus bis einschl. 09.09.2018 (Betriebsschluss) kommt es zu umfangreichen Fahrplanänderungen auf der Strecke Hamm ◄► Dortmund. Die Auswirkungen im Detail: RE 1 (Hamm ◄► Aachen) Die Züge werden zwischen Hamm und Dortmund ohne Halt über eine Güterzugstrecke umgeleitet Zusätzlich halten die Züge in Preußen RE 3 (Hamm ◄► Düsseldorf) Die Züge werden zwischen Hamm und Dortmund ohne Halt über eine Güterzugstrecke umgeleitet Zusätzlich halten die Züge in Dortmund-Derne und Dortmund-Kirchderne RE 6 (Minden / Bielefeld ◄► Köln/Bonn Flughafen) Die Züge fallen zwischen Dortmund Hbf und Hamm (Westf) aus RE 11 (Kassel / Paderborn / Hamm ◄► Düsseldorf) Sämtliche Züge werden zwischen Soest ◄► Bochum Hbf umgeleitet Zusätzlich halten die Züge in Werl, Unna und Dortmund-Hörde RB 51 (Dortmund Hbf ◄► Lünen Hbf – nur Zwischentakt) Die Kurztakte Dortmund ◄► Lünen (nicht Dortmund ◄► Coesfeld / Enschede) fallen aus. RB 50 (Dortmund Hbf ◄► Münster Hbf) Haltausfall Dortmund-Kirchderne RB 59 (Dortmund Hbf ◄► Soest) Ausfall des Zwischentaktes, dadurch nur noch 60-Minuten-Takt Schienenersatzverkehr Dortmund ◄► Kamen und Kamen ◄► Hamm 3 Fahrten pro Stunde und Richtung als Schnellbusse ohne Zwischenhalte und 3 Fahrten pro Stunde und Richtung als Busse mit allen Unterwegshalten. Buslinie S 30 (Dortmund ◄► Bergkamen) Zusätzliche Fahrten (2x stündlich) zwischen -
Germany Web 2006
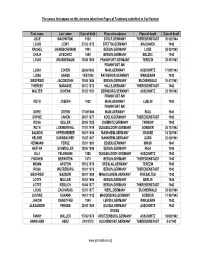
The names that appear on this list were taken from Pages of Testimony submitted to Yad Vashem First name Last name Date of birth Place of residence Place of death Date of death JULIE MACHNITSKI 1930 STOLP,GERMANY THERESIENSTADT 30/06/1944 LOUIS LEWY 27/02/1873 STETTIN,GERMANY MAJDANEK 1942 RACHEL GRABISCHEWSKI 1901 BERLIN,GERMANY LODZ 25/03/1942 CHAJA LIFSCHITZ 1892 BERLIN,GERMANY BELZEC 1943 LOUIS GRUENEBAUM 13/08/1869 FRANKFURT,GERMANY TEREZIN 28/01/1943 FRANKFURT AM LUCIA COHEN 26/06/1883 MAIN,GERMANY AUSCHWITZ 17/09/1943 LUISA GANSS 18/5/1898 RATHENOW,GERMANY WARSZAWA 1942 SIEGFRIED JACOBSOHN 15/08/1884 BERLIN,GERMANY BUCHENWALD 10/07/1941 THERESE MANASSE 26/12/1872 HALLE,GERMANY THERESIENSTADT 1942 WALTER SCHENK 21/02/1921 BERNBURG,GERMANY AUSCHWITZ 23/10/1942 FRANKFURT AM RUTH JOSEPH 1902 MAIN,GERMANY LUBLIN 1942 FRANKFURT AM SOFIE STERN 17/09/1894 MAIN,GERMANY RIGA 1941 SOPHIE CAHEN 29/07/1877 KOELN,GERMANY THERESIENSTADT 1942 ROSA GELLER 26/06/1925 CHEMNITZ,GERMANY TARNOW 1942 RUTH LOEWENTHAL 17/01/1919 DUESSELDORF,GERMANY SOBIBOR 30/11/1943 SALMON OPPENHEIMER 14/01/1865 MANNHEIM,GERMANY GRASSE 14/12/1941 HELENE DARNBACHER 13/05/1867 MANNHEIM,GERMANY GURS 23/06/1941 HERMANN FERSE 15/01/1881 ESSEN,GERMANY MINSK 1941 HERTHA SCHMOLLER 18/06/1896 BERLIN,GERMANY RIGA 1944 ELLI FELDMANN 1888 DUESSELDORF,GERMANY AUSCHWITZ 1943 FINCHEN BERNSTEIN 1875 BERLIN,GERMANY THERESIENSTADT 1943 MRIAM APSTEIN 19/12/1870 BRESLAU,GERMANY TEREZIN 1943 ROSA WUERZBURG 15/01/1875 BERLIN,GERMANY THERESIENSTADT 1943 SIEGFRIED BAZNIZKI 25/01/1889 MINGOLSHEIM,GERMANY -

Ratings Affirmed on Various German Savings Banks, Helaba, and Dekabank on Capital Strengthening and Integration
Ratings Affirmed On Various German Savings Banks, Helaba, And DekaBank On Capital Strengthening And Integration Primary Credit Analyst: Bernd Ackermann, Frankfurt (49) 69-33-999-153; [email protected] Secondary Contact: Harm Semder, Frankfurt (49) 69-33-999-158; [email protected] OVERVIEW • German savings banks are continuing to strengthen their capitalization despite earnings pressure from ultra-low interest rates. • They are also benefitting from sound economic conditions in Germany, leading to low credit losses and a strong inflow of stable retail deposits. • We are affirming our ratings on members of regional subgroups of savings banks in Westphalia-Lippe, and in Hesse and Thuringia including the central bank Landesbank Hessen-Thueringen, and on DekaBank Deutsche Girozentrale. • The outlook on DekaBank remains positive, reflecting the potential for stronger integration into the German savings banks. The outlooks on the other entities are stable. FRANKFURT (S&P Global Ratings) Aug. 19, 2016--S&P Global Ratings today affirmed its ratings on two regional subgroups of Germany's savings banks sector, including their central bank, and on DekaBank Deutsche Girozentrale, the sector's investment product and securities services provider. The outlooks on these banks remain unchanged. The affirmations follow our regular surveillance reviews of these entities in light of the recent publication of aggregate financial data by German regional and national savings banks associations. Specifically, we took the following actions: WWW.STANDARDANDPOORS.COM/RATINGSDIRECT AUGUST 19, 2016 1 1696704 | 300027913 Ratings Affirmed On Various German Savings Banks, Helaba, And DekaBank On Capital Strengthening And Integration • We affirmed the 'A+/A-1' long- and short-term credit ratings on 68 savings banks in Westphalia-Lippe (collectively Savings Banks Westphalia-Lippe; SWL). -

2021-05-28 Verzeichnis Der Vollzugsanstalten in Deutschland
Verzeichnis der Vollzugsanstalten in der Bundesrepublik Deutschland Postanschrift, Straßenanschrift Anstalts- Ort Bezeichnung Telefon / Telefax Amtskasse / Zahlstelle Land zstd. StVK bei dem LG kennzahl E-Mail / Web-Adresse Postfach 50 01 42, 52085 Aachen Zahlstelle JVA Aachen Krefelder Straße 251, 52070 Aachen Justizvollzugsanstalt Aachen Postbank Köln Nordrhein- 0553 Aachen (02 41) 91 73 - 0 / Fax: (02 41) 91 73 - 2 73 Aachen mit Sozialtherapeutischer Abteilung DE37 3701 0050 0521 1205 07 Westfalen [email protected] PBNKDEFF www.jva-aachen.nrw.de Justizvollzugsanstalt Vechta Obernstraße 40, 28832 Achim Achim Niedersachsen Abteilung Achim (0 42 02) 91 58 55 Zentrale Zahlstelle Justizvollzug Postfach 4 41 85, 74738 Adelsheim bei der Justizvollzugsanstalt Mosbach; für Dr.-Traugott-Bender-Straße 2, 74740 Adelsheim Schwäbisch Gmünd Baden- Jugendstrafe: 0801 Adelsheim Justizvollzugsanstalt Adelsheim (0 62 91) 28 - 0 / Fax: (0 62 91) 2 81 23 Anstaltskennung: AK01 Württemberg Jugendrichter beim [email protected] Baden-Württembergische Bank AG Adelsheim www.jva-adelsheim.de DE25 6005 0101 0004 5521 07 SOLADEST Zentrale Zahlstelle Justizvollzug Postfach 13 64, 74803 Mosbach bei der Justizvollzugsanstalt Mosbach; für Justizvollzugsanstalt Adelsheim Hauptstraße 106, 74821 Mosbach Schwäbisch Gmünd Baden- Jugendstrafe: 0802 Adelsheim Außenstelle Mosbach (0 62 61) 25 46 / Fax: (0 62 61) 89 38 60 Anstaltskennung: AK01 Württemberg Jugendrichter beim offener Vollzug [email protected] Baden-Württembergische Bank AG Adelsheim www.jva-adelsheim.de DE25 6005 0101 0004 5521 07 SOLADEST Postfach 13 80, 86544 Aichach auswärtige StVK Justizvollzugsanstalt Aichach Landesjustizkasse Bamberg Münchener Straße 33, 86551 Aichach des LG Augsburg b. Mit Abteilung für weibliche 7036 09034-8 (0 82 51) 9 07 - 0 / Fax: (0 82 51) 9 07 - 4 00 d.