DOCSLIB.ORG

Math 1330 Section 6.2 1 Section 7.1: Right-Triangle Applications in This Section, We'll Solve Right Triangles. in Some Proble

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Math 1330 Section 6.2 1 Section 7.1: Right-Triangle Applications in This Section, We'll Solve Right Triangles. in Some Proble Math 1330 Section 6.2 Section 7.1: Right-Triangle Applications In this section, we’ll solve right triangles. In some problems you will be asked to find one or two specific pieces of information, but often you’ll be asked to “solve the triangle,” which means that you will find all lengths and measures that were not given. You’ll use the six trigonometric functions of an angle to do this. In some cases, you will be able to use properties of the 30 ° − 60 ° − 90 °triangles or of 45 ° − 45 ° − 90 ° . Example 1: Calculate x and y from the figure below. y x 100cm 30 o Example 2: In ∆ABC with right angle C, ∠A = 46 ° and AC = 12. Find BC. Round to the answer to the nearest hundredth. Example 3: Find x and y in the triangle below. y 10 ft. 40 ° x 1 Math 1330 Section 6.2 Example 4: Draw a diagram to represent the given situation. Then find the indicated measures to the nearest degree. An isosceles triangle has sides measuring 20 inches, 54 inches and 54 inches. What are the measures of the angle? Angle of Elevation The angle of elevation is an angle that s formed by the horizontal ray and another ray above the horizontal. So when viewing an object at a point above the horizontal, the angle between the line of sight and horizontal is angle of elevation in the figure below. Example 5: Draw a diagram to represent the given situation. The find the indicate measure to the nearest tenth. The angle elevation to the top of a building from a point on the ground 125 feet away from the building is 8° . How tall is the building? 2 Math 1330 Section 6.2 Example 6: Draw a diagram to represent the given situation. The find the indicate measure to the nearest tenth. A 16-foot ladder leans against a building. The ladder forms an angle of 70 °with the ground. a) How high up the building does the ladder reach? b) What is the horizontal distance from the foot of the ladder to the base of the building? Angle of Depression The angle of depression is an angle that s formed by the horizontal ray and another ray below the horizontal. So when viewing an object at a point above the horizontal, the angle between the line of sight and horizontal is angle of elevation in the figure below. Example 7: Draw a diagram to represent the given situation. The find the indicate measure to the nearest tenth. Dave is at the top of a hill. He looks down and spots his car at a 61 °angle of depression. If the hill is 59 meters high, how far is his car from the base of the hill? 3 Math 1330 Section 6.2 Example 8: Mike stands 450 feet from the base of the Empire State Building and sights the top of the building. If the Empire State Building is 1,453 feet tall, approximate the angle of elevation from Mike’s perspective as he sights the top of the building. (Disregard Mike’s height in your calculations.) 4 Math 1330 Section 7.2 7.2 Area of a Triangle In this section, we’ll use a familiar formula and a new formula to find the area of a triangle. Given a b 1 Recall the area of a triangle is given by A = bh . We normally used this formula when we knew 2 the height of the triangle. However if the height is not given we must solve for it some way. So we solve for the height of the triangle by breaking the given triangle down into right triangles and use our trigonometric function (sine) to solve for the height. Area of a Trangle 1 A = ab sin θ 2 a, b are the lengths of two sides of a triangle θ is the angle between them. Example 1: Find the exact area of the triangle. 30 ° 11 Math 1330 Section 7.2 Example 2: Find the exact area of the triangle. 29 120 ° 17 Example 3: Find the area of an isosceles triangle with legs measuring 12 inches and the base angle is 30 degrees each. Example 4: If the area of ∆EFG is 30 in 2, e = 8 in. and g = 15 in, find all possible measures of angle F. Math 1330 Section 7.2 Example 5: A regular hexagon is inscribed in a circle of radius 6m. Find the area of the hexagon. Area of a Segment of a Circle You can also find the area of a segment of a circle. The shaded area of the picture is an example of a segment of a circle. B O A To find the area of a segment, find the area of the sector with central angle θ and radius OA. Then find the area of ∆OAB . Then subtract the area of the triangle from the area of the sector. 1 Area of a sector of a circle = r 2θ 2 − Area of the segment = Area sec tor Area triangle Example 6: Find the area of the segment of the circle with radius 6 meters and central angle 3π measuring . 4 Math 1330 Section 7.3 Section 7.3: Law of Sines and Law of Cosines Sometimes you will need to solve a triangle that is not a right triangle. This type of triangle is called an oblique triangle. To solve an oblique triangle you will not be able to use right triangle trigonometry. Instead, you will use the Law of Sines and/or the Law of Cosines. You will typically be given three parts of the triangle and you will be asked to find the other three. The approach you will take to the problem will depend on the information that is given. If you are given SSS (the lengths of all three sides) or SAS (the lengths of two sides and the measure of the included angle), you will use the Law of Cosines to solve the triangle. If you are given SAA (the measures of two angles and one side) or SSA (the measures of two sides and the measure of an angle that is not the included angle), you will use the Law of Sines to solve the triangle. Recall from your geometry course that SSA does not necessarily determine a triangle. We will need to take special care when this is the given information. Here’s the Law of Cosines. In any triangle ABC, = + − 2 cos = + − 2 cos = + − 2 cos The development of one case of this formula is given in detail in the online text. Here’s the Law of Sines. In any triangle ABC, sin sin sin = = The development of this formula is given in detail in the online text. Here are some facts about solving triangles that may be helpful in this section. If you are given SSS, SAS or SAA, the information determines a unique triangle. If you are given SSA, the information given may determine 0, 1 or 2 triangles. If this is the information you are given, you will have some additional work to do. Since you will have three pieces of information to find when solving a triangle, it is possible for you to use both the Law of Sines and the Law of Cosines in the same problem. When drawing a triangle, the measure of the largest angle is opposite the longest side; the measure of the middle-sized angle is opposite the middle-sized side; and the measure of the smallest angle is opposite the shortest side. Suppose a, b and c are suggested to be the lengths of the three sides of a triangle. Suppose that c is the biggest of the three measures. In order for a, b and c to form a triangle, this inequality must be true: a + b > c . So, the sum of the two smaller sides must be greater than the third side. 1 .
Load more

Recommended publications
  • Section 5.5 Right Triangle Trigonometry 385
    Section 5.5 Right Triangle Trigonometry 385 Section 5.5 Right Triangle Trigonometry In section 5.3 we were introduced to the sine and cosine function as ratios of the sides of a triangle drawn inside a circle, and spent the rest of that section discussing the role of those functions in finding points on the circle. In this section, we return to the triangle, and explore the applications of the trigonometric functions to right triangles where circles may not be involved. Recall that we defined sine and cosine as (x, y) y sin( θ ) = r r y x cos( θ ) = θ r x Separating the triangle from the circle, we can make equivalent but more general definitions of the sine, cosine, and tangent on a right triangle. On the right triangle, we will label the hypotenuse as well as the side opposite the angle and the side adjacent (next to) the angle. Right Triangle Relationships Given a right triangle with an angle of θ opposite sin( θ) = hypotenuse hypotenuse opposite adjacent cos( θ) = hypotenuse θ opposite adjacent tan( θ) = adjacent A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.” 386 Chapter 5 Example 1 Given the triangle shown, find the value for cos( α) . The side adjacent to the angle is 15, and the 17 hypotenuse of the triangle is 17, so 8 adjacent 15 cos( α) = = α hypotenuse 17 15 When working with general right triangles, the same rules apply regardless of the orientation of the triangle.
    [Show full text]
  • Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1
    Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1. Acute angle: Angle whose measure is greater than 0° and less than 90°. 2. Adjacent angles: Two angles that have a common side and a common vertex. 3. Alternate interior angles: A pair of angles in the interior of a figure formed by two lines and a transversal, lying on alternate sides of the transversal and having different vertices. 4. Altitude: Perpendicular segment from a vertex of a triangle to the opposite side or the line containing the opposite side. 5. Angle: A figure formed by two rays with a common endpoint. 6. Angle bisector: Ray that divides an angle into two congruent angles and bisects the angle. 7. Base Angles: Two angles not included in the legs of an isosceles triangle. 8. Bisect: To divide a segment or an angle into two congruent parts. 9. Coincide: To lie on top of the other. A line can coincide another line. 10. Collinear: Lying on the same line. 11. Complimentary: Two angle’s whose sum is 90°. 12. Concave Polygon: Polygon in which at least one interior angle measures more than 180° (at least one segment connecting two vertices is outside the polygon). 13. Conclusion: A result of summary of all the work that has been completed. The part of a conditional statement that occurs after the word “then”. 14. Congruent parts: Two or more parts that only have the same measure. In CPCTC, the parts of the congruent triangles are congruent. 15. Congruent triangles: Two triangles are congruent if and only if all of their corresponding parts are congruent.
    [Show full text]
  • Geometrygeometry
    Park Forest Math Team Meet #3 GeometryGeometry Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. Geometry: Angle measures in plane figures including supplements and complements 3. Number Theory: Divisibility rules, factors, primes, composites 4. Arithmetic: Order of operations; mean, median, mode; rounding; statistics 5. Algebra: Simplifying and evaluating expressions; solving equations with 1 unknown including identities Important Information you need to know about GEOMETRY… Properties of Polygons, Pythagorean Theorem Formulas for Polygons where n means the number of sides: • Exterior Angle Measurement of a Regular Polygon: 360÷n • Sum of Interior Angles: 180(n – 2) • Interior Angle Measurement of a regular polygon: • An interior angle and an exterior angle of a regular polygon always add up to 180° Interior angle Exterior angle Diagonals of a Polygon where n stands for the number of vertices (which is equal to the number of sides): • • A diagonal is a segment that connects one vertex of a polygon to another vertex that is not directly next to it. The dashed lines represent some of the diagonals of this pentagon. Pythagorean Theorem • a2 + b2 = c2 • a and b are the legs of the triangle and c is the hypotenuse (the side opposite the right angle) c a b • Common Right triangles are ones with sides 3, 4, 5, with sides 5, 12, 13, with sides 7, 24, 25, and multiples thereof—Memorize these! Category 2 50th anniversary edition Geometry 26 Y Meet #3 - January, 2014 W 1) How many cm long is segment 6 XY ? All measurements are in centimeters (cm).
    [Show full text]
  • Right Triangles and the Pythagorean Theorem Related?
    Activity Assess 9-6 EXPLORE & REASON Right Triangles and Consider △​ ABC​ with altitude ​​CD‾ ​​ as shown. the Pythagorean B Theorem D PearsonRealize.com A 45 C 5√2 I CAN… prove the Pythagorean Theorem using A. What is the area of △​ ​ABC? ​Of △​ACD? Explain your answers. similarity and establish the relationships in special right B. Find the lengths of ​​AD‾ ​​ and ​​AB‾ ​​. triangles. C. Look for Relationships Divide the length of the hypotenuse of △​ ABC​ VOCABULARY by the length of one of its sides. Divide the length of the hypotenuse of ​ △ACD​ by the length of one of its sides. Make a conjecture that explains • Pythagorean triple the results. ESSENTIAL QUESTION How are similarity in right triangles and the Pythagorean Theorem related? Remember that the Pythagorean Theorem and its converse describe how the side lengths of right triangles are related. THEOREM 9-8 Pythagorean Theorem If a triangle is a right triangle, If... ​△ABC​ is a right triangle. then the sum of the squares of the B lengths of the legs is equal to the square of the length of the hypotenuse. c a A C b 2 2 2 PROOF: SEE EXAMPLE 1. Then... ​​a​​ ​ + ​b​​ ​ = ​c​​ ​ THEOREM 9-9 Converse of the Pythagorean Theorem 2 2 2 If the sum of the squares of the If... ​​a​​ ​ + ​b​​ ​ = ​c​​ ​ lengths of two sides of a triangle is B equal to the square of the length of the third side, then the triangle is a right triangle. c a A C b PROOF: SEE EXERCISE 17. Then... ​△ABC​ is a right triangle.
    [Show full text]
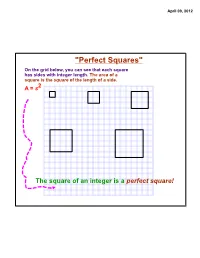
  • "Perfect Squares" on the Grid Below, You Can See That Each Square Has Sides with Integer Length
    April 09, 2012 "Perfect Squares" On the grid below, you can see that each square has sides with integer length. The area of a square is the square of the length of a side. A = s2 The square of an integer is a perfect square! April 09, 2012 Square Roots and Irrational Numbers The inverse of squaring a number is finding a square root. The square-root radical, , indicates the nonnegative square root of a number. The number underneath the square root (radical) sign is called the radicand. Ex: 16 = 121 = 49 = 144 = The square of an integer results in a perfect square. Since squaring a number is multiplying it by itself, there are two integer values that will result in the same perfect square: the positive integer and its opposite. 2 Ex: If x = (perfect square), solutions would be x and (-x)!! Ex: a2 = 25 5 and -5 would make this equation true! April 09, 2012 If an integer is NOT a perfect square, its square root is irrational!!! Remember that an irrational number has a decimal form that is non- terminating, non-repeating, and thus cannot be written as a fraction. For an integer that is not a perfect square, you can estimate its square root on a number line. Ex: 8 Since 22 = 4, and 32 = 9, 8 would fall between integers 2 and 3 on a number line. -2 -1 0 1 2 3 4 5 April 09, 2012 Approximate where √40 falls on the number line: Approximate where √192 falls on the number line: April 09, 2012 Topic Extension: Simplest Radical Form Simplify the radicand so that it has no more perfect-square factors.
    [Show full text]
  • Introduction to Geometry" ©2014 Aops Inc
    Excerpt from "Introduction to Geometry" ©2014 AoPS Inc. www.artofproblemsolving.com CHAPTER 12. CIRCLES AND ANGLES (a) Consider the circle with diameter OP. Call this circle . Why must hit O in at least two di↵erent C C points? (b) Why is it impossible for to hit O in three di↵erent points? Hints: 530 C (c) Let the points where hits O be A and B. Prove that \PAO = \PBO = 90 . C ◦ (d) Prove that PA and PB are tangent to O. (e)? Now for the tricky part – proving that these are the only two tangents. Suppose D is on O such that PD is tangent to O. Why must D be on ? Hints: 478 C (f) Why does the previous part tell us that PA! and PB! are the only lines through P tangent to O? 12.3.6? O is tangent to all four sides of rhombus ABCD, AC = 24, and AB = 15. (a) Prove that AC and BD meet at O (i.e., prove that the intersection of the diagonals of ABCD is the center of the circle.) Hints: 439 (b) What is the area of O? Hints: 508 12.4 Problems Problems Problem 12.19: A quadrilateral is said to be a cyclic quadrilateral if a circle can be drawn that passes through all four of its vertices. Prove that if ABCD is a cyclic quadrilateral, then \A + \C = 180◦. C Problem 12.20: In the figure, PC is tangent to the circle and PD 70◦ bisects \CPE. Furthermore, CD = 70◦, DE = 50◦, and \DQE = P B Q D 40◦.
    [Show full text]
  • Math 1330 - Section 4.1 Special Triangles
    Math 1330 - Section 4.1 Special Triangles In this section, we’ll work with some special triangles before moving on to defining the six trigonometric functions. Two special triangles are 30 − 60 − 90 triangles and 45 − 45 − 90 triangles. With little additional information, you should be able to find the lengths of all sides of one of these special triangles. First we’ll review some conventions when working with triangles. We label angles with capital letters and sides with lower case letters. We’ll use the same letter to refer to an angle and the side opposite it, although the angle will be a capital letter and the side will be lower case. In this section, we will work with right triangles. Right triangles have one angle which measures 90 degrees, and two other angles whose sum is 90 degrees. The side opposite the right angle is called the hypotenuse, and the other two sides are called the legs of the triangle. A labeled right triangle is shown below. B c a A C b Recall: When you are working with a right triangle, you can use the Pythagorean Theorem to help you find the length of an unknown side. In a right triangle ABC with right angle C, 2 2 2 a + b = c . Example: In right triangle ABC with right angle C, if AB = 12 and AC = 8, find BC. 1 Special Triangles In a 30 − 60 − 90 triangle, the lengths of the sides are proportional. If the shorter leg (the side opposite the 30 degree angle) has length a, then the longer leg has length 3a and the hypotenuse has length 2a.
    [Show full text]
  • Isosceles Triangles on a Geoboard
    Isosceles Triangles on a Geoboard About Illustrations: Illustrations of the Standards for Mathematical Practice (SMP) consist of several pieces, including a mathematics task, student dialogue, mathematical overview, teacher reflection questions, and student materials. While the primary use of Illustrations is for teacher learning about the SMP, some components may be used in the classroom with students. These include the mathematics task, student dialogue, and student materials. For additional Illustrations or to learn about a professional development curriculum centered around the use of Illustrations, please visit mathpractices.edc.org. About the Isosceles Triangles on a Geoboard Illustration: This Illustration’s student dialogue shows the conversation among three students who are looking for how many isosceles triangles can be constructed on a geoboard given only one side. After exploring several cases where the known side is one of the congruent legs, students then use the known side as the base and make an interesting observation. Highlighted Standard(s) for Mathematical Practice (MP) MP 1: Make sense of problems and persevere in solving them. MP 5: Use appropriate tools strategically. MP 7: Look for and make use of structure. Target Grade Level: Grades 6–7 Target Content Domain: Geometry Highlighted Standard(s) for Mathematical Content 7.G.A.2 Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle. Math Topic Keywords: isosceles triangles, geoboard © 2016 by Education Development Center. Isosceles Triangles on a Geoboard is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
    [Show full text]
  • Brahmagupta's Derivation of the Area of a Cyclic Quadrilateral
    Brahmagupta’s derivation of the area of a cyclic quadrilateral Satyanad Kichenassamy To cite this version: Satyanad Kichenassamy. Brahmagupta’s derivation of the area of a cyclic quadrilateral. Historia Mathematica, Elsevier, 2010, 37 (1), pp.28-61. 10.1016/j.hm.2009.08.004. halshs-00443604 HAL Id: halshs-00443604 https://halshs.archives-ouvertes.fr/halshs-00443604 Submitted on 12 Mar 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Historia Mathematica 37 (2010) 28{61 http://dx.doi.org/10.1016/j.hm.2009.08.004 Brahmagupta's derivation of the area of a cyclic quadrilateral Satyanad Kichenassamy1 Abstract. This paper shows that Propositions XII.21{27 of Brahmagupta's Br¯ahma- sphut.asiddh¯anta (628 a.d.) constitute a coherent mathematical discourse leading to the expression of the area of a cyclic quadrilateral in terms of its sides. The radius of the circumcircle is determined by considering two auxiliary quadrilaterals. Observing that a cyclic quadrilateral is split by a diagonal into two triangles with the same circumcenter and the same circumradius, the result follows, using the tools available to Brahmagupta. The expression for the diagonals (XII.28) is a consequence.
    [Show full text]
  • Geometry a Solutions
    Geometry A Solutions Written by Ante Qu 1. [3] Three circles, with radii of 1; 1; and 2, are externally tangent to each other. The minimum possiblep area of a quadrilateral that contains and is tangent to all three circles can be written as a + b c where c is not divisible by any perfect square larger than 1. Find a + b + c. Solution: In order to have the smallest quadrilateral, we want to make it tangent at as many points as possible. Consider the following quadrilateral. Note that 3 of the sides are fixed as 3 sides of a rectangle, so the area is proportional to the distance from the side tangential to the two small circles to the midpoint of the fourth side. This can be minimized by making the fourth side the fourth side of a rectangle, which is tangent to the large circle at its midpoint. To find the width of this rectangle, note that it is the sum of a radius of a small circle, a radius of the large circle, and the altitude of a isosceles trianglep with side lengths of 2; 3; 3. Using the Pythagorean Theorem, we find the altitude to be 2 p2. To calculate thep whole area of the rectangle, we multiply its height, 4, by its width, 3 + 2 2, to get 12 + 8 2. So a + b + c = 12 + 8 + 2 = 22 . 2. [3] Two circles centered at O and P have radii of length 5 and 6 respectively. Circle O passes through point P . Let the intersection points of circles O and P be M and N.
    [Show full text]
  • Right Triangles and Quadrilaterals
    Excerpt from "Prealgebra" (C) 2011 AoPS Inc. www.artofproblemsolving.com CHAPTER 12. RIGHT TRIANGLES AND QUADRILATERALS 12 12 12 12 12 12 12 1 2 5 24 11 12 18 3 7 Choose always the way that seems the best, however rough it may be; custom will soon render it easy and agreeable. – Pythagoras CHAPTER 12 Right Triangles and Quadrilaterals 12.1 The Pythagorean Theorem In a right triangle, the side of the triangle opposite the right angle is called hypotenuse the hypotenuse and the other two sides are called the legs of the triangle. We also often use the terms “legs” and “hypotenuse” to refer the lengths of leg the legs and hypotenuse of a right triangle. leg In this section, we explore one of the most famous math theorems, the Pythagorean Theorem, which is a powerful relationship among the sides of a right trian- gle. We’ll start by walking through one of the many proofs of the Pythagorean Theorem. (“Pythagorean” is pronounced “puh-thag-uh-ree-uhn.”) Problems Problem 12.1: Four identical right triangles with legs of lengths 3 P 4 X 3 Q and 4 are attached to the sides of square WXYZ as shown, such that PW = QX = RY = SZ = 3 and PX = QY = RZ = SW = 4. 3 4 (a) Explain why \PWS = 180◦, and why PQRS is a square. W (b) What is the area of PQRS? Y 4 (c) Find the area of WXYZ. 3 (d) Find WX. S 3 Z 4 R 442 Copyrighted Material Excerpt from "Prealgebra" (C) 2011 AoPS Inc.
    [Show full text]
  • 6.1 Basic Right Triangle Trigonometry
    6.1 Basic Right Triangle Trigonometry MEASURING ANGLES IN RADIANS First, let’s introduce the units you will be using to measure angles, radians. A radian is a unit of measurement defined as the angle at the center of the circle made when the arc length equals the radius. If this definition sounds abstract we define the radian pictorially below. Assuming the radius drawn below equals the arc length between the x-axis and where the radius intersects the circle, then the angle Θ is 1 radian. Note that 1 radian is approximately 57°. Θ ≈ 57° 1 Many people are more familiar with a degree measurement of an angle. Below is a quick formula for converting between degrees and radians. You may use this in order to gain a more intuitive understanding of the magnitude of a given radian measurement, but for most classes at R.I.T. you will be using radians in computation exclusively. 휋 푟푎푑푖푎푛푠 = 푑푒푔푟푒푒푠 180 Now consider the right triangle pictured below with sides a,b,c and angles A,B,C. We will be referencing this generic representation of a right triangle throughout the packet. B c a A C b BASIC FACTS AND DEFINITIONS 휋 1. Right angle: angle measuring radians (example: angle C above) 2 2. Straight angle: angle measuring π radians 휋 3. Acute angle: angle measuring between 0 and radians (examples: angles A and B 2 above) 휋 4. Obtuse angle: angle measuring between and π radians 2 휋 5. Complementary angles: Two angles whose sum is radians. Note that A and B are 2 휋 complementary angles since C = radians and all triangles have a sum of π radians 2 between the three angles.
    [Show full text]