Forecastability of Land Prices: a Local Modelling Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
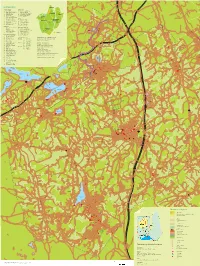
Nurmijärven Matkailu Ja Ulkoilukartta
NURMIJÄRVI NÄHTÄVYYDET RATSASTUS 1 Aleksis Kiven patsas 39 Islanninhevostalli Dynur 2 Aleksis Kiven syntymäkoti 55 Mintzun issikkatalli 3 Aleksis Kivi -huone 42 Nurmijärven Ratsastuskoulu 4 Klaukkalan kirkko 41 Perttulan Ratsastuskeskus 5 Museokahvila 44 Ratsastuskoulu Solbacka 6 Nukarin koulumuseo 53 Vuonotalli Solsikke 3 Nurmijärven Kirjastogalleria 7 Nurmijärven kirkko UINTI 2 Puupiirtäjän työhuone 45 Herusten uimapaikka 8 Pyhän Nektarioksen kirkko 46 Röykän uimapaikka 9 Rajamäen kirkko 35 Sääksjärven uimaranta 10 Taaborinvuoren museoalue 47 Tiiran uimaranta 11 Vanha hautausmaa 48 Vaaksin uimapaikka 49 Rajamäen uimahalli PALVELUT 12 Nurmijärven kunnanvirasto MAJOITUSPAIKKOJA Kirjastot 32 Holman kurssikeskus 13 Klaukkalan kirjasto 50 Hyvinvointikeskus Haukilampi 3 Nurmijärven pääkirjasto 34 Ketolan strutsitila 14 Rajamäen kirjasto 15 Hotelli Kiljavanranta 51 Lomakoti Kotoranta ELÄMYKSIÄ JA LUONTOA 54 Nukarin lomamökit 18 Alhonniitun ulkoilualue 53 Vuonotalli Solsikke 52 Ali-Ollin Alpakkatila 56 Bowling House TYÖPAIKKA-ALUEET MITEN MERKATAAN KUNTORADAT? 25 Maaniitun-Ihantolan Klaukkala A Järvihaka Kuntoratakartan värikoodit ei toimi tässä. liikuntapuisto B Pietarinmäki Numeroinnilla pelkästään?... 30 Frisbeegolfrata C Ristipakka Rajamäen liikuntapuisto Nurmijärvi D Alhonniittu 19 Isokallion ulkoilualue E Ilvesvuori Rajamäki – Kehityksen maja 20 Klaukkalan jäähalli F Karhunkorpi Kehityksen Majan kilpalatu 21 Klaukkalan urheilualue G Kuusimäki Märkiön lenkki (Kehityksen majalta) 22 Tarinakoru Rajamäki H Ketunpesä Matkun lenkki (Kehityksen -

Space to Live and to Grow in the Helsinki Region Welcome to Nurmijärvi
In English Space to live and to grow in the Helsinki region Welcome to Nurmijärvi Hämeenlinna 40 min Choose the kind of environment that you prefer to live in: an urban area close Tampere 1 h 20 min to services, or a rural environment close to nature. Hanko 2 h 10 min Kehä III Nurmijärvi centre Enjoy the recreational facilities on offer: there are cultural and other events – (Outer ring road) 12 min also for tourists, and there are possibilities to exercise and enjoy nature almost Hyvinkää 20 min outside your own front door. Services from the Helsinki Metropolitan Area add to Helsinki 30 min the offering. Estimated times from the E12 junction near the centre of Nurmijärvi Benefit from a wide range of services that take into account your life situation: from early childhood to basic education and further training, and later on, elderly General facts Main population people are offered a high standard of care. • Surface area: 367 km2 centres • Inhabitants: over 40 000 • Klaukkala: 40 % Your business will be ideally located, making logistics easy to arrange: a short • Under 15-yearsElinvoimaa old: 25 % ja• Nurmijärvielämisen centre: 20 % distance from the ports and airport, you’ll benefit from good road communications tilaa Helsingin• Rajamäki: seudulla 18 % in both east-west and north-south directions, while being away from the rush. Choose your workplace and your journey to work: apart from your own munici- HYVINKÄÄ pality, the Helsinki Metropolitan Area and the municipalities to the north are near Lahteen neighbours. Tampereelle MÄNTSÄLÄ 25 POR- Klaukkala Rajamäki NAI- Nurmijärvi offers all this – a large enough municipality to be able to provide the nec- JÄRVENPÄÄ NEN essary services and infrastructure for modern life, as well as to grow and develop E 12 Kirkonkylä continuously, but still small enough to provide a living space at a competitive cost. -

Horace Alan Seibert
Petteri Elo CURRICULUM VITAE Mailing Address: Prinssintie 5, 01260 Vantaa, Finland Electronic Mail: [email protected] Telephone: +358405506020 Date of Birth: February 28, 1974 Wife: Anna-Helena Elo, Master of Education, Special Education Teacher, Vice-Principle Children: Paavo Elo Samuel Elo EDUCATION Emerging Educational Leadership, April 2013, Helsinki Board of Education Educational Leadership, August 2012, Finnish National Board of Education Supervising Teacher for Student Teachers, November 2011, University of Helsinki Master of Education, Educational Science and Pedagogy, June 2007, University of Helsinki Bachelor of Education, June 2006, University of Helsinki Bachelor of Science, Economics, June 1997, University of Kent at Canterbury, United Kingdom WORK EXPERIENCE PedaNow – Educational Consulting and Training Founder, CEO and Consultant January 2015-present Education First (EF) – Professional Learning Tours January 2015-present Member of concept development team. University of Helsinki Center for Continuing Education HY+ Network Trainer January 2017 – present Polar Partners Member of the Expert Pool August 2017 - present xEdu – Business Accelerator January 2017-present Pedagogical mentor for start-ups. FulBright Scholar September 2015 – December 2015 Responsible for developing the education system in Virginia with the local educators. Consulting Teacher for the Helsinki Educational Department on Metacognitions and Higher Order Thinking Skills, August 2013 – July 2016 Responsible for consulting the curriculum process, writing the curriculum and providing in-service training for teachers, principals and administrators. Class Teacher, Hiidenkivi Comprehensive School, Helsinki, Finland August 2015 – present Head Teacher, Class Teacher, Hiidenkivi Comprehensive School, Helsinki, Finland August 2011 –July 2015 Together with the management group responsible for designing pedagogical development in Hiidenkivi Comprehensive School. Emphasis is on developing the teaching of metacognitive skills, knowledge and experience to every single student in our school. -

Lisämuutoksia Nurmijärven Linja-Autoliikenteessä 1.1.2015 Alkaen
TIEDOTE 18.12.2014 Lisämuutoksia Nurmijärven linja-autoliikenteessä 1.1.2015 alkaen Nurmijärven linja-autoliikenteeseen on tehty lisämuutoksia 1.1.2015 alkaen. Linjan 934 (Klaukkala-Myyrmäki) jat- kamisesta uudella linjatunnuksella 954 on tiedotettu jo aiemmin. Yhteydet Hyrylään Jotta Keudan opiskelijoiden kulkeminen joukkoliikennettä käyttäen olisi jatkossakin mahdollista, on rakennettu vaihdolliset yhteydet Rajamäeltä ja Nurmijärven Kirkonkylästä Hyrylään ja takaisin. Vaihdot tapahtuvat Palojoen koululla tai Nahkelassa Seutulantien risteyksen kohdalla. Vaihdollisten yhteyksien aikataulut ovat tiedotteen liittee- nä. Nykyiseen palvelutasoon ei päästä, mutta kokonaisuutta tarkastellaan vielä vuoden 2015 puolella. Nykyisellään klo 6.40 Nahkelasta Helsinkiin lähtevä vuoro lähtee jatkossa Palojoelta klo 6.45 Helsinkiin, ja siihen on vaihtoyhteys sekä Rajamäeltä että Kirkonkylältä. Paluuvuoroa Helsingistä samalla tavalla ei toistaiseksi ole pystytty järjestämään. Lahnuksen suunta Nykyisen linjan 339 (vuoden 2015 alusta 355) vuorot harvenevat ja sunnuntailiikenne lakkaa 1.1.2015 lukien. Linjan aikataulut on suunniteltu siten, että nurmijärveläisten työmatkakulkeminen Lahnuksen kautta on yhä mahdollista, ja yhteyksiä vesipuisto Serenaan on säilytetty. Kustannussyistä palvelutason parannukset on suunnattu ruuhkai- semmille yhteysväleille eli Hämeenlinnanväylälle Nurmijärven eri osista. Liput Nurmijärven nuorisolipun uusia vyöhykkeitä (Nurmijärveltä Espooseen/Vantaalle tai Helsinkiin) myydään kunnan alueella sekä Kampissa sijaitsevissa Matkahuollon -

20200616 Presentations Virtual NWM Website Version
Welcome to the virtual Network Meeting! 28th Network Meeting, May 26th 2020 Please mute your microphone Ask questions via the chat We will start at 10:00 Good morning & welcome Hans Ruijter, NETLIPSE Chairman, Rijkswaterstaat (the Netherlands) Rules during this meeting: . Please mute your microphone to avoid background noise. Only the presenters will have their microphones on. Please use the chat function on the right hand side of your screen for questions and ideas and to answer any questions the presenters ask you. If you are experiencing any problems, contact Geertje van Engen via phone or sms. The presentations will be made available on the website after the meeting. Main topics at this meeting: . Dealing with contractor delays and payment in this crisis situation . Danish government policy; Storstrøm Bridge project (DK) and Oosterweel project (B) . How organisations are using the crisis to speed up projects . Rail projects North of England and the Finnish government perspective . How to guarantee safety on sites during the crisis and organise effective communication . Dutch and German government experiences Managing large projects in a crisis situation Welcome and opening Introduction of the programme and our ‘online rules of engagement’. 10:00 – 10:05 Hans Ruijter, NETLIPSE Chairman (The Netherlands) Pau Lian Staal-Ong, NETLIPSE Director (The Netherlands) Dealing with contractors 10:05 – 10:45 How to deal with your contractors in this crisis situation? How do you cope with delays and penalties? Do you have special pre-payment agreements? Danish perspective (government policy and the Storstrøm Bridge project) 10:05 – 10:20 Helle Lange, Director of Procurement, Vejdirektoratet (Denmark) Vibeke Schiøler Sørensen, Legal Counsellor, Vejdirektoratet (Denmark) Belgium perspective (the Oosterweel project) 10:20 – 10:30 Peter Vanhoegaerden, COO, Lantis (Belgium) 10:30 – 10:45 Interactive discussion. -

Transport System Planning in the Helsinki Region Helsinki Regional Transport Authority
Transport system planning in the Helsinki region Helsinki Regional Transport Authority Tuire Valkonen, transport planner Contents 1. Helsinki Regional Transport Authority HRT in general 2. Helsinki Region Transport System Plan (HLJ) • The role of the plan • Background • Preparation process • HLJ 2015 policies • Examples of measures • How we cummunicate with citizens? What does HRT do? • Is responsible for the preparation of the Helsinki Region Transport System Plan (HLJ). • Plans and organizes public transport in the region and works to improve its operating conditions. • Procures bus, tram, Metro, ferry and commuter train services. • Approves the public transport fare and ticketing system as well as public transport fares. • Is responsible for public transport marketing and passenger information. • Organizes ticket sales and is responsible for ticket inspection. HRT’s basic structure (c. 360 persons) The location of the Helsinki Region in Europe HRT area and HLJ planning area Municipalities of the Keski-Uusimaa Region (KUUMA) • Land area approximately 3700 km2 • Population 1.38 million According to its charter, HRT may expand to cover all 14 municipalities in the Helsinki region. HRT Region 1.1.2012 Cities of the Helsinki 6 Metropolitan Area The main networks and terminals Nationally significant public transport terminal International airport Harbor Railway Raiway for freight traffic Metroline High way Main road Regional way In process… Ring Rail Line The west metro Helsinki Region Transport System Planning The role of the Helsinki Region Transport System Plan (HLJ) • A long-term strategic plan that considers the transport system as a whole. • Aligns regional transport policy and guidelines primary measures for the development of the transport system. -

Environmental References
Environmental References 1. ENVIRONMENTAL IMPACT ASSESSMENT AND LICENSING 2. ENVIRONMENTAL ECONOMICS 3. ENVIRONMENTAL AND SAFETY MANAGEMENT 4. CLIMATE CHANGE STRATEGIES 1. ENVIRONMENTAL IMPACT ASSESSMENT AND LICENSING CUSTOMER PROJECT YEAR Katternö, Finland Environmental Impact Assessment of a 280 000 t/a waste incin- 2003 - eration plant producing electricity and heat in the town of Pietar- 2004 saari Componenta Oy, Finland Environmental Impact Assessment of Foundry 2004 Hyvinkään Lämpövoima Oy Environmental Impact Assessment of a 150 000 t/a waste incin- 2004 eration plant producing electricity and heat in the Town of Hy- vinkää KSS Energia Oy, Finland Environmental Licensing of the Hinkismäki combined-cycle power 2004 plant Seinäjoen Energia Oy, Finland Environmental impact assessment of waste and sludge treatment 2003 - and energy recovery in Seinäjoki, Finland 2004 Porin Lämpövoima Oy, Finland Environmental impact assessment of a 150 000 t/a waste incinera- 2003 - tion plant producing electricity and heat in the City of Pori 2004 Mäntän Energia Oy, Finland Environmental licensing of an industrial power plant in Mänttä 2003 J.M. Huber Finland Oy Environmental licensing of a sodium silicate plant in Taavetti, 2003 Luumäki Oulu Energy, Finland Environmental licensing of a waste incineration plant in Oulu 2003 E.ON Oyj, Finland Environmental licensing of the Suomenoja power plant, Espoo 2003 Turun Jätelaitos ja Turun Seudun Environmental impact assessment of waste and sludge treatment 2003 Puhdistamo Oy, Finland and energy recovery in -

KILPAILUKOHTEEN MÄÄRITTELY Nurmijärven Sisäisen
UUDELY/xxxx/2017 Etelä-Savo TARJOUSPYYNNÖN LIITE 3 KILPAILUKOHTEEN MÄÄRITTELY Nurmijärven sisäisen, Nurmijärven ja Hyvinkään välisen sekä Nurmijärven ja Helsingin/Vantaan/Espoon välisen linja-autoliikenteen palvelutasovaatimukset ja kuvaus nykyisestä liikenteestä 1. Palvelutasomäärittelyn soveltaminen käyttöoikeussopimuksessa Liikenteen palvelutasomäärittely perustuu Uudenmaan ELY-keskuksen laatimaan palvelutasomäärittelyyn (Uudenmaan ELY-keskuksen raportteja 78/2016). Palvelutasojen määrälliset tekijät on esitetty taulukoissa 1 ja 2. (nämä löytyvät myös julkaisusta Liikenneviraston ohjeita 31/2015). Yhteysvälikohtainen palvelutaso on esitetty karttakuvassa sekä taulukossa 3. taulukoiden liikennöintiaikoja tulkitaan siten että ääripäiden tarjonta kohdistetaan päämatkustussuuntaan. Esimerkiksi palvelutasoluokassa III aamun ensimmäisten vuorojen Helsingin suuntaan tulee lähteä viimeistään noin klo 6:00, mutta Helsingin suunnasta ei tarvitse lähteä vuoroa Nurmijärven suuntaan samaan aikaan. Taulukko 1 Talviliikenteen määrälliset palvelutasotekijät. HUOM: Tässä taulukossa esitetty ruuhka-aika poikkeaa julkaisun 31/2015 mukaisesta! 6.00-21.30 6.00-20.00 6.00-21.30 6.00-20.00 Ruuhka (n. klo 6-9 ja 15-18) 2/4 Taulukko 2 Kesäliikenteen määrälliset palvelutasotekijät Kuva 1. Taulukossa 3 esitettyjen yhteysvälien palvelutasoluokat. 3/4 Taulukko 3 Kooste yhteysväleistä ja niiden palvelutasoluokasta Klaukkala – Helsinki Luokka III, pohjoisempaa tulevan liikenteen kanssa Sisältää yhteyden Mäntysalo –Klaukkala yhteisellä (vt3:n) osuudella luokka II. -

Nurmijärven JOUKKOLIIKENTEEN KESÄAIKATAULUT
Nurmijärven JOUKKOLIIKENTEEN KESÄAIKATAULUT 1.6. – 12.8.2020 Liikennöintikauden vaihtumisessa on vaihtelua liikennöitsijöittäin. Tarkista aikataulut tarvittaessa liikennöitsijältä tai Matkahuollosta. Koosteen on tuottanut: NURMIJÄRVEN KUNTA Kunta ei vastaa aikataulukirjan sisällöstä. MATKUSTAJALLE Tähän Nurmijärven kunnan julkaisemaan koosteeseen on kerätty aikataulut tärkeimmistä asukkaita palvelevista joukkoliikenneyhteyksistä ajalle 1.6.–12.8.2020. Liikennöintikauden vaihtumisessa voi olla liikennöitsijäkohtaisia eroja. Aikataulujulkaisu ei sisällä Nurmijärven kunnan kaikkien palvelulinjojen reitti- tai aikataulutietoja. Aikataulujulkaisu on tehty liikennöitsijöiden ilmoittamien muutostietojen avulla. Nurmijärven kunta ottaa mielellään vastaan tietoja puutteista tai virheistä sekä aikataulun kehitysideoita. Joukkoliikenteen aikataulut ja muuta tietoa mm. lipputuotteista on tarjolla Uudenmaan joukkoliikenteen infosivuilla www.uudenmaanjoukkoliikenne.fi. Liikennöitsijöiden Internet-sivuilta löydät tuoreimmat aikataulutiedot ja tiedot mahdollisista muutoksista. Lisäksi joukkoliikennetietoa löytyy kuntien sivuilta: www.jarvenpaa.fi www.pornainen.fi www.nurmijarvi.fi www.mantsala.fi www.tuusula.fi www.hyvinkaa.fi Tässä aikataulukoosteessa esitettyjen linjojen lisäksi Nurmijärven yhteyksiä palvelevat Keski-Uudenmaan ja pääkaupunkiseudun väliset linjat. Katso aikataulujulkaisu ”Keski-Uudenmaan ja pääkaupunkiseudun välinen bussiliikenne”. NURMIJÄRVEN KUNNAN YHTEYSHENKILÖ: Riku Hellgren [email protected] puh. 040 317 2357 LIIKENNÖITSIJÄN -

Statue of Liberty and Oppression Finland Watches Closely As Estonia’S Statue Crisis Unfolds
ISSUE 1 • 9 – 15 MAY 2007 • €3 INTERNATIONAL NEWS FINLAND NEWS SPORT Mamma Mia! Afghan - Finland’s Lions CULTURE page 16 foreign nuclear need a forces debate killer Nokia unveils train together hots up instinct Barracuda page 12 page 7 page 5 BUSINESS page 10 LEHTIKUVA / HEIKKI SAUKKOMAA Statue of liberty and oppression Finland watches closely as Estonia’s statue crisis unfolds ESTONIA'S prime minister Andrus fence of Estonia, while appealing Ansip has appealed for calm dur- to both Russia and Estonia to calm ing the anniversary of the Soviet tensions. Red Army’s World War Two victo- Estonia has been shocked by ry over Nazi Germany. Victory Day the riots in which one person died, events are held in Estonia and Rus- more than 150 were injured, and sia on Tuesday and Wednesday. about 800 people were arrest- The controversial relocation of ed. A national debate has ensued a monument to the Red Army sol- about the strained relationship be- diers who died during World War tween the Estonian majority and Two sparked riots by Russian res- Russian minority of the country’s idents in Tallinn, Estonia’s capi- population. tal city, on 27 April. The disputed The political repercussions of bronze soldier – a symbol of libera- the crisis have also been felt across tion from Nazism for the Russians Europe, not least in Finland. Rus- and a symbol of Soviet oppression sia’s readiness to threaten Estonia for Estonians – now stands in the by orchestrating a siege of its em- military cemetery in Tallinn. bassy in Moscow, cutting oil sup- The Victory Day events are be- plies and restricting trade, has Andorra’s Anonymous perform their song Let’s save the World during the Eurovision Song Contest rehearsals in Helsinki. -

1. Seutuliikenne Pääkaupunkiseudulle
1. SEUTULIIKENNE PÄÄKAUPUNKISEUDULLE Vihdintie - Klaukkala - suunta Uusi Vanha linjanro linjanro Reitti Liikennöitsijä Muuta Kamppi - Vihdintie - Lahnus - Klaukkala 355 339 ( - Mäntysalo - Metsäkylä - Nurmijärvi) Nurmijärven Linja Ei liikennöi sunnuntaisin Hämeenlinnanväylä - Klaukkala -suunta Uusi Vanha linjanro linjanro Reitti Liikennöitsijä Muuta Kamppi - Hämeenlinnanväylä - Klaukkala Ei pysähdy välillä Ruskeasuo - 454 491 (-Mäntysalo) PIKAVUORO Nurmijärven Linja Nurmijärven raja Kamppi - Hämeenlinnanväylä - Klaukkala 455 491 ( - Mäntysalo - Metsäkylä - Nurmijärvi) Nurmijärven Linja Kamppi - Hämeenlinnanväylä - Klaukkala 456 492 - Perttula - Nurmijärvi (- Rajamäki) Nurmijärven Linja Kamppi - Hämeenlinnanväylä - Klaukkala - 457 490 Perttula - Röykkä - Rajamäki ( - Nurmijärvi) Nurmijärven Linja Kamppi - Hämeenlinnanväylä - Klaukkala 480 ( - Vihti / Karkkila / Loppi) Kivistö Kamppi - Hämeenlinnanväylä - Klaukkala - Ei pysähdy välillä Ruskeasuo - 481 Röykkä PIKAVUORO Kivistö Nurmijärven raja Kamppi - Hämeenlinnanväylä - Klaukkala - 486 Perttula - Röykkä - Karkkila Pohjolan Liikenne Kamppi - Hämeenlinnanväylä - Klaukkala 487 ( Perttula - Röykkä - Karkkila / Loppi) Pekola-yhtiöt Ajetaan Vanhaa Hämeenlin- 954 934 Klaukkala-Myyrmäki Nurmijärven Linja nantietä Hämeenlinnanväylä - Nurmijärvi -suunta Uusi Vanha linjanro linjanro Reitti Liikennöitsijä Muuta Kamppi - Hämeenlinnanväylä - Moottoritie Ei pysähdy välillä Ruskeasuo - 463 490/495 - Nurmijärvi (- Rajamäki) PIKAVUORO Nurmijärven Linja Nurmijärven raja Kamppi - Hämeenlinnanväylä - Moottoritie -

URBAN FORM in the HELSINKI and STOCKHOLM CITY REGIONS City Regions from the Perspective of Urban Form and the Traffic System
REPORTS OF THE FINNISH ENVIRONMENT INSTITUTE 16 | 2015 This publication compares the development of the Helsinki and Stockholm AND CAR ZONES TRANSPORT PUBLIC DEVELOPMENT OF PEDESTRIAN, CITY REGIONS AND STOCKHOLM THE HELSINKI URBAN FORM IN city regions from the perspective of urban form and the traffic system. Urban Form in the Helsinki The viewpoint of the study centres on the notion of three urban fabrics – and Stockholm City Regions walking city, transit city and car city – which differ in terms of their physical structure and the travel alternatives they offer. Development of Pedestrian, Public Transport and Car Zones Based on the results of the study, growth in the Stockholm region has been channelled inward more strongly than in Helsinki, which has increased the structural density of Stockholm’s core areas. During recent years, however, Panu Söderström, Harry Schulman and Mika Ristimäki the Helsinki region has followed suit with the direction of migration turning from the peri-urban municipalities towards the city at the centre. FINNISH ENVIRONMENT INSTITUTE FINNISH ENVIRONMENT ISBN 978-952-11-4494-3 (PDF) ISSN 1796-1726 (ONLINE) Finnish Environment Institute REPORTS OF THE FINNISH ENVIRONMENT INSTITUTE 16 / 2015 Urban Form in the Helsinki and Stockholm City Regions Development of pedestrian, public transport and car zones Panu Söderström, Harry Schulman and Mika Ristimäki REPORTS OF THE FINNISH ENVIRONMENT INSTITUTE 16 | 2015 Finnish Environment Institute Sustainability of land use and the built environment / Environmental Policy Centre Translation: Multiprint Oy / Multidoc Layout: Panu Söderström Cover photo: Panu Söderström The publication is also available in the Internet: www.syke.fi/publications | helda.helsinki.fi/syke ISBN 978-952-11-4494-3 (PDF) ISSN 1796-1726 (online) 2 Reports of the Finnish Environment Institute 16/2015 PREFACE In recent decades, the Helsinki and Stockholm city regions have been among the most rapidly growing areas in Europe.