DOCSLIB.ORG

The Equations of Linear Elasticity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Equations of Linear Elasticity Chapter 5 The equations of linear elasticity 5.1 Summary of equations • Strain-displacement relations: 1 e = (u + u ) (5.1) ij 2 i;j j;i • Equilibrium equations/equations of motion: @2u τ + F = ρ i (5.2) ij;j i @t2 • Constitutive equations: τij = λδij ekk + 2µeij (5.3) 5.2 Displacement formulation: The Navier-Lam´e equations • Solve for the displacements: @2u (λ + µ)u + µu + F = ρ i (5.4) k;ki i;kk i @t2 or symbolically: @2u (λ + µ) grad div u + µr2u + F = ρ ; (5.5) @t2 which is equivalent to: @2u (λ + 2µ) grad div u − µ curl curl u + F = ρ : (5.6) @t2 • This is a system of three coupled linear elliptic PDEs for the three displacements ui(xj ). 5.3 Stress formulation: The static Beltrami-Mitchell equations • For static deformations, we have 1 − ν 1 − ν τ +F = 0 or symbolically r2θ + div F = 0: (5.7) 1 + ν ii;jj i;i 1 + ν θ;jj and the stresses fulfil the|{zBeltrami-Mitc} hell equations: 1 ν τ + τ + δ F +F + F = 0: (5.8) ij;kk 1 + ν kk;ij 1 − ν ij k;k j;i i;j r2 τij θ;ij div F | {z } | {z } |{z} • (5.8) represents a system of six coupled linear elliptic PDEs for the six stress components τij (xj ). When these have been determined, the strains can be recovered from (4.6) or (4.16). Then the displacements follow from (5.1). They are only determined up to arbitrary rigid body motions. 12 MT30271 Elasticity: The equations of linear elasticity 13 5.4 Simplifications for F = const:: • For constant (or vanishing!) body force, the stress, strain and displacement components are bihar- monic functions, ui;jjkk = 0 τij;kkll = 0 eij;kkll = 0 (5.9) or symbolically: 4 4 4 r u = 0 r τij = 0 r eij = 0: (5.10) • The dilation and the trace of the stress tensor are harmonic functions: uj;jkk = d;kk = 0 τjj;kk = θ;kk = 0 (5.11) or symbolically: r2d = 0 r2θ = 0 (5.12) • Note that in (5.4) { (5.8) F acts as an inhomogeneity in a system of linear equations. The system can be transformed into a homogeneous system for uh = u−up (with different boundary conditions) if a particular solution up (which does not have to fulfil the boundary conditions) can be found. 5.5 Boundary conditions: (0) • Displacement (Dirichlet) boundary conditions: Prescribed displacement field ui . (0) uij@D = ui (5.13) (0) • Stress (Neumann) boundary conditions: Prescribed (applied) traction ti on boundary. Note that nj is the outer unit normal vector on the elastic body. (0) tij@D = τij nj j@D = ti (5.14) • Mixed (Robin) boundary conditions { `elastic foundation' represented by the stiffness tensor kij . Physically, this implies that the traction which the elastic foundation exerts on the body is propor- (0) tional to the boundary displacement. This can be combined with an applied traction ti as in the Neumann case. (0) (ti + kij uj ) j@D = (τij nj + kij uj ) j@D = ti (5.15) MT30271 Elasticity: The equations of linear elasticity 14 Governing Equations in Cylindrical Polar Coordinates • x1 = x = r cos θ, x2 = y = r sin θ, x3 = z = z. u = (ur; uθ; uz); e = (eij ); τ = (τij ); where i; j = r; θ; z. • Vector calculus: @f 1 @f @f 1 @(ru ) 1 @u @u grad f = ^r + θ^ + z^; div u = r + θ + z ; @r r @θ @z r @r r @θ @z 1 @u @u @u @u 1 @(ru ) 1 @u curl u = z − θ ^r + r − z θ^ + θ − r z^: r @θ @z @z @r r @r r @θ • Stress-strain relations have the same form as in Cartesian coordinates: τij = λδij div u + 2µeij ; i; j = r; θ; z: • Stress-displacement relations: @ur 1 @uθ ur @uz τrr = λ div u + 2µ ; τθθ = λ div u + 2µ + ; τzz = λ div u + 2µ ; @r r @θ r @z τ τ @u u 1 @u τ τ @u @u τ τ 1 @u @u rθ = θr = θ − θ + r ; rz = zr = z + r ; θz = zθ = z + θ : µ µ @r r r @θ µ µ @r @z µ µ r @θ @z • Strain-displacement relations: @u 1 @u u @u e = r ; e = θ + r ; e = z ; rr @r θθ r @θ r zz @z @u u 1 @u @u @u 1 @u @u 2e = 2e = θ − θ + r ; 2e = 2e = r + z ; 2e = 2e = z + θ : rθ θr @r r r @θ rz zr @z @r zθ θz r @θ @z • Equilibrium equations (statics): for the displacement formulation, use Navier's equation, (λ + 2µ) grad div u − µ curl curl u + F = 0; whereas for the stress formulation, use @τ 1 @τ @τ τ − τ rr + rθ + rz + rr θθ + F = 0 @r r @θ @z r r @τ 1 @τ @τ 2 rθ + θθ + θz + τ + F = 0 @r r @θ @z r rθ θ @τ 1 @τ @τ 1 rz + θz + zz + τ + F = 0: @r r @θ @z r rz z • Stress boundary conditions: these are when t is prescribed. We have, from ti = n^j τij , tr = n^rτrr + n^θτrθ + n^zτrz tθ = n^rτrθ + n^θτθθ + n^zτθz tz = n^rτrz + n^θτθz + n^zτzz MT30271 Elasticity: The equations of linear elasticity 15 Governing Equations in Spherical Polar Coordinates • x1 = x = r sin θ cos φ, x2 = y = r sin θ sin φ, x3 = z = r cos θ. u = (ur; uθ; uφ); e = (eij ); τ = (τij ); where i; j = r; θ; φ. • Vector calculus: @f 1 @f 1 @f grad f = ^r + θ^ + φ^; @r r @θ r sin θ @φ 1 @ 2 @ @ div u = (r sin θ ur) + (r sin θ uθ) + (ruφ) ; r2 sin θ @r @θ @φ ^r rθ^ r sin θ φ^ 1 curl u = @ @ @ : r2 sin θ @r @θ @φ u ru r sin φ u r θ φ • Stress-strain relations have the same form as in Cartesian coordinates: τij = λδij div u + 2µeij; i; j = r; θ; φ. • Stress-displacement relations: @ur 2µ @uθ τrr = λ div u + 2µ ; τθθ = λ div u + + ur ; @r r @θ 2µ 1 @uφ τrθ τθr @uθ uθ 1 @ur τφφ = λ div u + + ur + uθ cot θ ; = = − + ; r sin θ @φ µ µ @r r r @θ τ τ 1 @u @u u τ τ 1 @u 1 @u u cot θ rφ = φr = r + φ − φ ; θφ = φθ = θ + φ − φ : µ µ r sin θ @φ @r r µ µ r sin θ @φ r @θ r • Strain-displacement relations: @u 1 @u u 1 @u u u cot θ e = r ; e = θ + r ; e = φ + r + θ ; rr @r θθ r @θ r φφ r sin θ @φ r r @u u 1 @u 1 @u @u u 2e = 2e = θ − θ + r ; 2e = 2e = r + φ − φ ; rθ θr @r r r @θ rφ φr r sin θ @φ @r r 1 @u 1 @u u cot θ 2e = 2e = θ + φ − φ : φθ θφ r sin θ @φ r @θ r • Equilibrium equations (statics): for the displacement formulation, use Navier's equation, (λ + 2µ) grad div u − µ curl curl u + F = 0; whereas for the stress formulation, use @τ 1 @τ 1 @τ 2τ − τ − τ + cot θ τ rr + rθ + rφ + rr θθ φφ rθ + F = 0 @r r @θ r sin θ @φ r r @τ 1 @τ 1 @τ 3τ + (τ − τ ) cot θ rθ + θθ + θφ + rθ θθ φφ + F = 0 @r r @θ r sin θ @φ r θ @τ 1 @τ 1 @τ 3τ + 2τ cot θ rφ + θφ + φφ + rφ θφ + F = 0: @r r @θ r sin θ @φ r φ • Stress boundary conditions: these are when t is prescribed. We have, from ti = n^j τij , tr = n^rτrr + n^θτrθ + n^φτrφ tθ = n^rτrθ + n^θτθθ + n^φτθφ tφ = n^rτrφ + n^θτθφ + n^φτφφ.
Load more

Recommended publications
  • Arxiv:1910.01953V1 [Cond-Mat.Soft] 4 Oct 2019 Tion of the Load
    Geometric charges and nonlinear elasticity of soft metamaterials Yohai Bar-Sinai,1 Gabriele Librandi,1 Katia Bertoldi,1 and Michael Moshe2, ∗ 1School of Engineering and Applied Sciences, Harvard University, Cambridge MA 02138 2Racah Institute of Physics, The Hebrew University of Jerusalem, Jerusalem, Israel 91904 Problems of flexible mechanical metamaterials, and highly deformable porous solids in general, are rich and complex due to nonlinear mechanics and nontrivial geometrical effects. While numeric approaches are successful, analytic tools and conceptual frameworks are largely lacking. Using an analogy with electrostatics, and building on recent developments in a nonlinear geometric formu- lation of elasticity, we develop a formalism that maps the elastic problem into that of nonlinear interaction of elastic charges. This approach offers an intuitive conceptual framework, qualitatively explaining the linear response, the onset of mechanical instability and aspects of the post-instability state. Apart from intuition, the formalism also quantitatively reproduces full numeric simulations of several prototypical structures. Possible applications of the tools developed in this work for the study of ordered and disordered porous mechanical metamaterials are discussed. I. INTRODUCTION tic metamaterials out of an underlying nonlinear theory of elasticity. The hallmark of condensed matter physics, as de- A theoretical analysis of the elastic problem requires scribed by P.W. Anderson in his paper \More is Dif- solving the nonlinear equations of elasticity while satis- ferent" [1], is the emergence of collective phenomena out fying the multiple free boundary conditions on the holes of well understood simple interactions between material edges - a seemingly hopeless task from an analytic per- elements. Within the ever increasing list of such systems, spective.
    [Show full text]
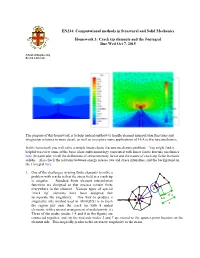
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • Linear Elasticity
    10 Linear elasticity When you bend a stick the reaction grows noticeably stronger the further you go — until it perhaps breaks with a snap. If you release the bending force before it breaks, the stick straightens out again and you can bend it again and again without it changing its reaction or its shape. That is elasticity. Robert Hooke (1635–1703). In elementary mechanics the elasticity of a spring is expressed by Hooke’s law English physicist. Worked on elasticity, built tele- which says that the force necessary to stretch or compress a spring is propor- scopes, and the discovered tional to how much it is stretched or compressed. In continuous elastic materials diffraction of light. The Hooke’s law implies that stress is proportional to strain. Some materials that we famous law which bears his name is from 1660. usually think of as highly elastic, for example rubber, do not obey Hooke’s law He stated already in 1678 except under very small deformation. When stresses grow large, most materials the inverse square law for gravity, over which he deform more than predicted by Hooke’s law. The proper treatment of non-linear got involved in a bitter elasticity goes far beyond the simple linear elasticity which we shall discuss in controversy with Newton. this book. The elastic properties of continuous materials are determined by the under- lying molecular structure, but the relation between material properties and the molecular structure and arrangement in solids is complicated, to say the least. Luckily, there are broad classes of materials that may be described by a few Thomas Young (1773–1829).
    [Show full text]
  • Linear Elastostatics
    6.161.8 LINEAR ELASTOSTATICS J.R.Barber Department of Mechanical Engineering, University of Michigan, USA Keywords Linear elasticity, Hooke’s law, stress functions, uniqueness, existence, variational methods, boundary- value problems, singularities, dislocations, asymptotic fields, anisotropic materials. Contents 1. Introduction 1.1. Notation for position, displacement and strain 1.2. Rigid-body displacement 1.3. Strain, rotation and dilatation 1.4. Compatibility of strain 2. Traction and stress 2.1. Equilibrium of stresses 3. Transformation of coordinates 4. Hooke’s law 4.1. Equilibrium equations in terms of displacements 5. Loading and boundary conditions 5.1. Saint-Venant’s principle 5.1.1. Weak boundary conditions 5.2. Body force 5.3. Thermal expansion, transformation strains and initial stress 6. Strain energy and variational methods 6.1. Potential energy of the external forces 6.2. Theorem of minimum total potential energy 6.2.1. Rayleigh-Ritz approximations and the finite element method 6.3. Castigliano’s second theorem 6.4. Betti’s reciprocal theorem 6.4.1. Applications of Betti’s theorem 6.5. Uniqueness and existence of solution 6.5.1. Singularities 7. Two-dimensional problems 7.1. Plane stress 7.2. Airy stress function 7.2.1. Airy function in polar coordinates 7.3. Complex variable formulation 7.3.1. Boundary tractions 7.3.2. Laurant series and conformal mapping 7.4. Antiplane problems 8. Solution of boundary-value problems 1 8.1. The corrective problem 8.2. The Saint-Venant problem 9. The prismatic bar under shear and torsion 9.1. Torsion 9.1.1. Multiply-connected bodies 9.2.
    [Show full text]
  • 20. Rheology & Linear Elasticity
    20. Rheology & Linear Elasticity I Main Topics A Rheology: Macroscopic deformation behavior B Linear elasticity for homogeneous isotropic materials 10/29/18 GG303 1 20. Rheology & Linear Elasticity Viscous (fluid) Behavior http://manoa.hawaii.edu/graduate/content/slide-lava 10/29/18 GG303 2 20. Rheology & Linear Elasticity Ductile (plastic) Behavior http://www.hilo.hawaii.edu/~csav/gallery/scientists/LavaHammerL.jpg http://hvo.wr.usgs.gov/kilauea/update/images.html 10/29/18 GG303 3 http://upload.wikimedia.org/wikipedia/commons/8/89/Ropy_pahoehoe.jpg 20. Rheology & Linear Elasticity Elastic Behavior https://thegeosphere.pbworks.com/w/page/24663884/Sumatra http://www.earth.ox.ac.uk/__Data/assets/image/0006/3021/seismic_hammer.jpg 10/29/18 GG303 4 20. Rheology & Linear Elasticity Brittle Behavior (fracture) 10/29/18 GG303 5 http://upload.wikimedia.org/wikipedia/commons/8/89/Ropy_pahoehoe.jpg 20. Rheology & Linear Elasticity II Rheology: Macroscopic deformation behavior A Elasticity 1 Deformation is reversible when load is removed 2 Stress (σ) is related to strain (ε) 3 Deformation is not time dependent if load is constant 4 Examples: Seismic (acoustic) waves, http://www.fordogtrainers.com rubber ball 10/29/18 GG303 6 20. Rheology & Linear Elasticity II Rheology: Macroscopic deformation behavior A Elasticity 1 Deformation is reversible when load is removed 2 Stress (σ) is related to strain (ε) 3 Deformation is not time dependent if load is constant 4 Examples: Seismic (acoustic) waves, rubber ball 10/29/18 GG303 7 20. Rheology & Linear Elasticity II Rheology: Macroscopic deformation behavior B Viscosity 1 Deformation is irreversible when load is removed 2 Stress (σ) is related to strain rate (ε ! ) 3 Deformation is time dependent if load is constant 4 Examples: Lava flows, corn syrup http://wholefoodrecipes.net 10/29/18 GG303 8 20.
    [Show full text]
  • Design of a Meta-Material with Targeted Nonlinear Deformation Response Zachary Satterfield Clemson University, [email protected]
    Clemson University TigerPrints All Theses Theses 12-2015 Design of a Meta-Material with Targeted Nonlinear Deformation Response Zachary Satterfield Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_theses Part of the Mechanical Engineering Commons Recommended Citation Satterfield, Zachary, "Design of a Meta-Material with Targeted Nonlinear Deformation Response" (2015). All Theses. 2245. https://tigerprints.clemson.edu/all_theses/2245 This Thesis is brought to you for free and open access by the Theses at TigerPrints. It has been accepted for inclusion in All Theses by an authorized administrator of TigerPrints. For more information, please contact [email protected]. DESIGN OF A META-MATERIAL WITH TARGETED NONLINEAR DEFORMATION RESPONSE A Thesis Presented to the Graduate School of Clemson University In Partial Fulfillment of the Requirements for the Degree Master of Science Mechanical Engineering by Zachary Tyler Satterfield December 2015 Accepted by: Dr. Georges Fadel, Committee Chair Dr. Nicole Coutris, Committee Member Dr. Gang Li, Committee Member ABSTRACT The M1 Abrams tank contains track pads consist of a high density rubber. This rubber fails prematurely due to heat buildup caused by the hysteretic nature of elastomers. It is therefore desired to replace this elastomer by a meta-material that has equivalent nonlinear deformation characteristics without this primary failure mode. A meta-material is an artificial material in the form of a periodic structure that exhibits behavior that differs from its constitutive material. After a thorough literature review, topology optimization was found as the only method used to design meta-materials. Further investigation determined topology optimization as an infeasible method to design meta-materials with the targeted nonlinear deformation characteristics.
    [Show full text]
  • Geometric Charges and Nonlinear Elasticity of Two-Dimensional Elastic Metamaterials
    Geometric charges and nonlinear elasticity of two-dimensional elastic metamaterials Yohai Bar-Sinai ( )a , Gabriele Librandia , Katia Bertoldia, and Michael Moshe ( )b,1 aSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138; and bRacah Institute of Physics, The Hebrew University of Jerusalem, Jerusalem, Israel 91904 Edited by John A. Rogers, Northwestern University, Evanston, IL, and approved March 23, 2020 (received for review November 17, 2019) Problems of flexible mechanical metamaterials, and highly A theoretical analysis of the elastic problem requires solv- deformable porous solids in general, are rich and complex due ing the nonlinear equations of elasticity while satisfying the to their nonlinear mechanics and the presence of nontrivial geo- multiple free boundary conditions on the holes’ edges—a seem- metrical effects. While numeric approaches are successful, ana- ingly hopeless task from an analytic perspective. However, direct lytic tools and conceptual frameworks are largely lacking. Using solutions of the fully nonlinear elastic equations are accessi- an analogy with electrostatics, and building on recent devel- ble using finite-element models, which accurately reproduce the opments in a nonlinear geometric formulation of elasticity, we deformation fields, the critical strain, and the effective elastic develop a formalism that maps the two-dimensional (2D) elas- coefficients, etc. (6). The success of finite-element (FE) simula- tic problem into that of nonlinear interaction of elastic charges. tions in predicting the mechanics of perforated elastic materials This approach offers an intuitive conceptual framework, qual- confirms that nonlinear elasticity theory is a valid description, itatively explaining the linear response, the onset of mechan- but emphasizes the lack of insightful analytical solutions to ical instability, and aspects of the postinstability state.
    [Show full text]
  • On the Path-Dependence of the J-Integral Near a Stationary Crack in an Elastic-Plastic Material
    On the Path-Dependence of the J-integral Near a Stationary Crack in an Elastic-Plastic Material Dorinamaria Carka and Chad M. Landis∗ The University of Texas at Austin, Department of Aerospace Engineering and Engineering Mechanics, 210 East 24th Street, C0600, Austin, TX 78712-0235 Abstract The path-dependence of the J-integral is investigated numerically, via the finite element method, for a range of loadings, Poisson's ratios, and hardening exponents within the context of J2-flow plasticity. Small-scale yielding assumptions are employed using Dirichlet-to-Neumann map boundary conditions on a circular boundary that encloses the plastic zone. This construct allows for a dense finite element mesh within the plastic zone and accurate far-field boundary conditions. Details of the crack tip field that have been computed previously by others, including the existence of an elastic sector in Mode I loading, are confirmed. The somewhat unexpected result is that J for a contour approaching zero radius around the crack tip is approximately 18% lower than the far-field value for Mode I loading for Poisson’s ratios characteristic of metals. In contrast, practically no path-dependence is found for Mode II. The applications of T or S stresses, whether applied proportionally with the K-field or prior to K, have only a modest effect on the path-dependence. Keywords: elasto-plastic fracture mechanics, small scale yielding, path-dependence of the J-integral, finite element methods 1. Introduction The J-integral as introduced by Eshelby [1,2] and Rice [3] is perhaps the most useful quantity for the analysis of the mechanical fields near crack tips in both linear elastic and non-linear elastic materials.
    [Show full text]
  • A Formulation of Stokes's Problem and the Linear Elasticity Equations Suggested by the Oldroyd Model for Viscoelastic Flow (*)
    M2AN. MATHEMATICAL MODELLING AND NUMERICAL ANALYSIS -MODÉLISATION MATHÉMATIQUE ET ANALYSE NUMÉRIQUE J. BARANGER D. SANDRI A formulation of Stokes’s problem and the linear elasticity equations suggested by the Oldroyd model for viscoelastic flow M2AN. Mathematical modelling and numerical analysis - Modéli- sation mathématique et analyse numérique, tome 26, no 2 (1992), p. 331-345 <http://www.numdam.org/item?id=M2AN_1992__26_2_331_0> © AFCET, 1992, tous droits réservés. L’accès aux archives de la revue « M2AN. Mathematical modelling and nume- rical analysis - Modélisation mathématique et analyse numérique » implique l’accord avec les conditions générales d’utilisation (http://www.numdam.org/ conditions). Toute utilisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fi- chier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ rr3n rn MATHEMATICAL MOOELUMG AND NUMERICAL ANAIYSIS M\!\_)\ M0DÉUSAT10N MATHÉMATIQUE ET ANALYSE NUMÉRIQUE (Vol. 26, n° 2, 1992, p. 331 à 345) A FORMULATION OF STOKES'S PROBLEM AND THE LINEAR ELASTICITY EQUATIONS SUGGESTED BY THE OLDROYD MODEL FOR VISCOELASTIC FLOW (*) L BARANGER (X), D. SANDRI O Communicated by R. TEMAM Abstract. — We propose a three fields formulation of Stokes' s problem and the équations of linear elasticity, allowing conforming finite element approximation and using only the classical inf-sup condition relating velocity
    [Show full text]
  • Elastic Plastic Fracture Mechanics Elastic Plastic Fracture Mechanics Presented by Calvin M
    Fracture Mechanics Elastic Plastic Fracture Mechanics Elastic Plastic Fracture Mechanics Presented by Calvin M. Stewart, PhD MECH 5390-6390 Fall 2020 Outline • Introduction to Non-Linear Materials • J-Integral • Energy Approach • As a Contour Integral • HRR-Fields • COD • J Dominance Introduction to Non-Linear Materials Introduction to Non-Linear Materials • Thus far we have restricted our fractured solids to nominally elastic behavior. • However, structural materials often cannot be characterized via LEFM. Non-Linear Behavior of Materials • Two other material responses are that the engineer may encounter are Non-Linear Elastic and Elastic-Plastic Introduction to Non-Linear Materials • Loading Behavior of the two materials is identical but the unloading path for the elastic plastic material allows for non-unique stress- strain solutions. For Elastic-Plastic materials, a generic “Constitutive Model” specifies the relationship between stress and strain as follows n tot =+ Ramberg-Osgood 0 0 0 0 Reference (or Flow/Yield) Stress (MPa) Dimensionaless Constant (unitless) 0 Reference (or Flow/Yield) Strain (unitless) n Strain Hardening Exponent (unitless) Introduction to Non-Linear Materials • Ramberg-Osgood Constitutive Model n increasing Ramberg-Osgood −n K = 00 Strain Hardening Coefficient, K = 0 0 E n tot K,,,,0 n=+ E Usually available for a variety of materials 0 0 0 Introduction to Non-Linear Materials • Within the context of EPFM two general ways of trying to solve fracture problems can be identified: 1. A search for characterizing parameters (cf. K, G, R in LEFM). 2. Attempts to describe the elastic-plastic deformation field in detail, in order to find a criterion for local failure.
    [Show full text]
  • Equilibrium of Two-Dimensional Cycloidal Pantographic Metamaterials in Three-Dimensional Deformations
    S S symmetry Article Equilibrium of Two-Dimensional Cycloidal Pantographic Metamaterials in Three-Dimensional Deformations Daria Scerrato † and Ivan Giorgio *,† International Research Center on Mathematics and Mechanics of Complex Systems—MeMoCS, Università degli studi dell’Aquila, 67100 L’Aquila, Italy; [email protected] * Correspondence: [email protected] † These authors contributed equally to this work. Received: 17 November 2019; Accepted: 13 December 2019; Published: 16 December 2019 Abstract: A particular pantographic sheet, modeled as a two-dimensional elastic continuum consisting of an orthogonal lattice of continuously distributed fibers with a cycloidal texture, is introduced and investigated. These fibers conceived as embedded beams on the surface are allowed to be deformed in a three-dimensional space and are endowed with resistance to stretching, shearing, bending, and twisting. A finite element analysis directly derived from a variational formulation was performed for some explanatory tests to illustrate the behavior of the newly introduced material. Specifically, we considered tests on: (1) bias extension; (2) compressive; (3) shear; and (4) torsion. The numerical results are discussed to some extent. Finally, attention is drawn to a comparison with other kinds of orthogonal lattices, namely straight, parabolic, and oscillatory, to show the differences in the behavior of the samples due to the diverse arrangements of the fibers. Keywords: non-linear elasticity; second gradient models; woven fabrics; metamaterials 1. Introduction In recent decades, metamaterials has attracted the attention of the scientific community considerably. They are artificially constructed materials characterized by an interior architecture that is designed with the aim of producing an optimized combination of responses to specific external excitation.
    [Show full text]
  • 9/21/07 Linear Elasticity-9 Stress Field and Momentum Balance. Imagine
    ES240 Solid Mechanics Fall 2007 Stress field and momentum balance. Imagine the three-dimensional body again. At time t, the material particle (x, y, z) is under a state of stress ! ij (x, y, z,t). Denote the distributed external force per unit volume by b(x, y, z,t). An example is the gravitational force, bz = !"g. The stress and the displacement are time-dependent fields. Each material particle has the acceleration 2 2 vector ! ui / !t . Cut a small differential element, of edges dx, dy and dz. Let ! be the density. The mass of the differential element is !dxdydz . Apply Newton’s second law in the x-direction, and we obtain that dydz[$ xx (x + dx, y, z,t)"$ xx (x, y, z,t)] + dxdz[$ yx (x, y + dy, z,t)"$ yx (x, y, z,t)] 2 ! ux + dxdy[$ zx (x, y, z + dz,t)"$ zx (x, y, z,t)]+ bxdxdydz = #dxdydz !t 2 Divide both sides of the above equation by dxdydz, and we obtain that 2 !# !# yx !# ! u xx + + zx + b = " x . !x !y !z x !t 2 9/21/07 Linear Elasticity-9 ES240 Solid Mechanics Fall 2007 This is the momentum balance equation in the x-direction. Similarly, the momentum balance equations in the y- and z-direction are !# !# !# !2u yx + yy + zy + b = " y !x !y !z y !t 2 2 !# !# yz !# ! u xz + + zz + b = " z !x !y !z z !t 2 When the body is in equilibrium, we drop the acceleration terms from the above equations. Using the summation convention, we write the three equations of momentum balance as 2 !# ij ! ui + bj = " 2 .
    [Show full text]