DOCSLIB.ORG

A Geometric Proof of Riemann Hypothesis ∑

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Geometric Proof of Riemann Hypothesis ∑ A Geometric Proof of Riemann Hypothesis Kaida Shi Department of Mathematics, Zhejiang Ocean University, Zhoushan City, Zip.316004, Zhejiang Province, China Abstract Beginning from the resolution of Riemann Zeta functionζ (s) , using the inner product formula of infinite-dimensional vectors in the complex space, the author proved the world’s problem Riemann hypothesis raised by German mathematician Riemannn in 1859. Keywords: complex space, solid of rotation, axis-cross section, bary-centric coordinate, inner product between two infinite-dimensional vectors in complex space. MR(2000): 11M 1 Introduction In 1859, German mathematician B. Riemann raised six very important hypothesizes aboutζ (s) in his thesis entitled Ueber die Anzahl der Primzahlen unter einer gegebenen Große [1] . Since his thesis was published for 30 years, five of the six hypothesizes have been solved satisfactorily. The remained one is the Super baffling problemRiemann hypothesis. That is the non-trivial zeroes of the Riemann 1 Zeta functionζ (s) are all lie on the straight line Re(s) = within the complex plane s. The well- 2 known Riemann Zeta function ζ ()s raised by Swiss mathematician Leonard Euler on 1730 to 1750. In 1749, he had proved the Riemann Zeta functionζ ()s satisfied another function equation. For Re(s) > 1, the series 1 1 1 1 +++++ 1sss2 3 LLn s is convergent, it can be defined asζ ()s . Although the definitional domain of the Riemann Zeta ∞ 1 function is , but German mathematician Hecke used the ζ (s) = ∑ s (s = σ + it) Re(s) > 1 n=1 n 1 analytic continuation method to continue this definitional domain to whole complex plane (except Re(s) = 1). In 1914, English mathematician G. H. Hardy declared that he had proved Riemann Zeta function 1 ζ ()s equation has infinite non-trivial zeroes lie on the straight line Re(s ) = . 2 In fact, about the Riemann Zeta functional equality ss1− −−s 1− s πζπ2 ΓΓ()()s = 2 ( )( ζ1− s ), (*) 2 2 because 1 1− 1 − 2 1 1 − 2 1− 1 1 π 2 Γ( 2 )ζ ( ) = π 2 Γ( 2 )ζ (1− ), 2 2 2 2 1 1 therefore, we have discovered that the solution of above equality is s = , namely Re(s) = . 2 2 1 That is to say no matter how the value t takes, σ always equals to . This explains that the 2 definitional domain of the Riemann Zeta function ζ (s) can be continued to at least 1 Re(s) = . 2 2 The formal resolution of Riemann Zeta function ζ ()s Considering the geometric meaning of the Riemann Zeta function 1 1 1 1 , ζ (s) = s + s + s +L+ s +L 1 2 3 n we will have the following figure: 2 w C(1) A1 1 A 2 1 s 1 B1 B2 A 3 2 s 1 B3 3 s O D1(1) D2(2) D3(3) … z Fig. 1 In above figure, the areas of the rectangles ADOCADDB11,,, 2 211 ADDB 3322L are respectively: 1 1 1 , s , s , s , L 1 2 3 therefore, the geometric meaning of the Riemann Zeta functionζ ()s is the sum of the areas of a series of rectangles within the complex space s. Using the inner product formula between two infinite-dimensional vectors, the Riemann Zeta functionζ ()s equation 1 1 1 1 ζ ()s =+++++=0 ()s = σ + it 1sss2 3 LLn s can be resolved as 1 1 1 1 1 1 1 1 ( σ , σ , σ ,L, σ ,L) ⋅ ( it , it , it ,L, it ,L) = 0. 1 2 3 n 1 2 3 n So, we should have (Please refer to the Appendix in the end) 1 1 1 1 1 1 1 1 rr +++++⋅⋅++++cos(NN , )= 0 , (1) 1222σσσ2 3 LLn 2 σ 1222it2 it3 itLLn 2 it 12 but in the complex space, if the inner product between two vectors equals to zero, then these two vectors 3 r r π are perpendicular, namely, (N , N ) = , therefore 1 2 2 r r cos(NN12 , )= 0 . So long as the values of two radical expressions in the left side of (1) are finite (real or imaginary), then we think the expression (1) is tenable. Because Riemann had proved that when Re(s) > 1, the equation ζ (s) = 0 has no solutions; when Re(s) < 0 , the Riemann Zeta function ζ ()s has only the trivial zeroes such as s = −2, −4, −6, L , therefore, the non-trivial zeroes of the Riemann Zeta function ζ ()s will lie on the banded domain 0 ≤ σ < 1. This explains that German mathematician Hecke used the analytic continuation method to continue the definitional domain of the Riemann Zeta function ζ ()s is tenable. 3 The relationship between the volume of the rotation solid and the area of its axis-cross section within the complex space 1 From the expression (1), we can know that when Re(s) = σ = , the series (harmonic series) 2 r r within the first radical expression of left side is divergent. Because cos(NN12 , )= 0 , therefore the situation of the complex series within the second radical expression of left side will change unable to research. Hence, we must transform the Riemann Zeta functionζ ()s equation. For this aim, let’s derive the relationship between the volume of the rotation solid and the area of its axis-cross section within the complex space. We call the cross section which pass through the axis z and intersects the rotation solid as axis- cross section. According to the barycentric formula of the complex plane lamina: 4 b ∫ zf[() z− gzdz ()] ξ = a , b [()fz− gzdz ()] ∫a b 1 22 2 [()()]fz− gzdz ∫a η = b . [()fz− gzdz ()] ∫a we have b π [()()]fz22− gzdz ∫a 2πη = b . (**) [()fz− gzdz ()] ∫a The numerator of the fraction of right side of the formula (**) is the volume of the rotation solid, and the denominator is the area of the axis-cross section. Theη of left side of the formula (**) is the longitudinal coordinate of the barycenter of axis-cross section. Its geometric explanation is: taking the axis-cross section around the axis z to rotate the angle of 2π , we will obtain the volume of the rotation solid. 4 The proof of divergence of two concerned serieses ∞ ∞ Now, let’s prove the divergence of the series ∑ cos(4tn ln ) and the series ∑sin(4t ln n) . n=1 n=1 y ytx= cos(4 ln ) ()t = 2 1 0 1 2 3 4 5 6 7 8 x -1 Fig. 2 ∞ Obviously, from Fig.2, we can find that the area of c ⋅ ∑ cos(4t ln n) is contained by the area n=1 5 +∞ of cos(4t ln x)dx . ∫ 1 Suppose that c is a very small positive number, then the sum of the areas of a series of rectangles (which take cos(4123tnn ln )(= , , ,L ) as high and take c as width) is: ∞ c ⋅ ∑ cos(4t ln n) = c ⋅ cos(4t ln1) + c ⋅cos(4t ln 2) + c ⋅cos(4t ln 3) +L. n=1 Because +∞ 1 w cos(4t ln x)dx = lim x[cos(4t ln x) + 4t sin(4t ln x)]1 ∫ 1 w→+∞ 2 t→∞ 1+16t 1 = lim [w(cos(4t ln w) + 4t sin(4t ln w)) −1] w→+∞ 2 t→∞ 1+16t w 1 4t 1 = lim cos(4t ln w) + sin(4t ln w) − lim w→+∞ 2 2 2 t→∞ 2 t→∞ 1+16t 1+16t 1+16t 1+16t 1 4t Suppose that = sinδ and = cosδ , then above equals to 1+16t 2 1+16t 2 w 1 lim sin(δ + 4t ln w) − lim w→+∞ 2 t→∞ 2 t→∞ 1+16t 1+16t d = lim sin(δ + 4t ln w) w→+∞ 1 t→∞ +16 t 2 d = lim sin(δ + 4t ln w). 4 w→+∞ t→∞ Because the relationship between w and t is linear, therefore, we denote w = dt . Obviously, d d d − ≤ lim sin(δ + 4t ln w) ≤ , 4 4 w→+∞ 4 t→∞ therefore 6 d ∞ d − ≤ c ⋅ ∑cos(4t ln n) ≤ , 4 n=1 4 namely, d ∞ d − ≤ ∑cos(4t ln n) ≤ . 4c n=1 4c ∞ Thus, although the series ∑ cos(4t ln n) is divergent, but it is oscillatory and bounded. n=1 ∞ Similarly, although the series ∑sin(4t ln n) is divergent, but it is also oscillatory and bounded. n=1 ∞ In a word, when t = 0 , the series ∑ cos(4t ln n) is divergent (goes to infinite); when t ≠ 0 , n=1 it is oscillatory and bounded. ∞ Thus, the divergence (oscillatory and bounded) of ∑ cos(4t ln n) has been proved. n=1 Similarly, we can prove the divergence (oscillatory and bounded) of the series ∞ ∑sin(4t ln n) (t ≠ 0) . n=1 . 5 Two theorems and their corollaries Suppose that 1−s 1 − 1− s ξπζ()sss=− (1 )2 Γ ( ) (1− s ), 2 2 then, we have ξ(s) = ζ (s) . According to the following: 7 [2] Theorem 1 The function ξ()s is the one class integer function, it has infinite zero points ρ n , ∞ ∞ −1 −−1 ε ， 01≤≤Re(ρ n ) , the series ∑ ρ n is divergent. But for ∀ ε > 0 the series ∑ ρ n is n=1 n=1 convergent. The zeroes of the functionξ()s are non-trivial zeroes of the Riemann Zeta function. We can obtain: [2] Corollary 1 The formula s ∞ s ξ()se=−ABs+ ∏1 e ρn n=1 ρ n is tenable. Corollary 2[2] The non-trivial zeroes of the Riemann Zeta function ζ ()s distribute 1 symmetrically on the straight line Re s = and Ims = 0 . 2 i t σ 0 + it2 σ1 + it0 • • •σ 2 + it0 1 o Re s = 2 σ σ 0 + it1 • Fig.
Load more

Recommended publications
  • Generalized Riemann Hypothesis Léo Agélas
    Generalized Riemann Hypothesis Léo Agélas To cite this version: Léo Agélas. Generalized Riemann Hypothesis. 2019. hal-00747680v3 HAL Id: hal-00747680 https://hal.archives-ouvertes.fr/hal-00747680v3 Preprint submitted on 29 May 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Generalized Riemann Hypothesis L´eoAg´elas Department of Mathematics, IFP Energies nouvelles, 1-4, avenue de Bois-Pr´eau,F-92852 Rueil-Malmaison, France Abstract (Generalized) Riemann Hypothesis (that all non-trivial zeros of the (Dirichlet L-function) zeta function have real part one-half) is arguably the most impor- tant unsolved problem in contemporary mathematics due to its deep relation to the fundamental building blocks of the integers, the primes. The proof of the Riemann hypothesis will immediately verify a slew of dependent theorems (Borwien et al.(2008), Sabbagh(2002)). In this paper, we give a proof of Gen- eralized Riemann Hypothesis which implies the proof of Riemann Hypothesis and Goldbach's weak conjecture (also known as the odd Goldbach conjecture) one of the oldest and best-known unsolved problems in number theory. 1. Introduction The Riemann hypothesis is one of the most important conjectures in math- ematics.
    [Show full text]
  • A Short and Simple Proof of the Riemann's Hypothesis
    A Short and Simple Proof of the Riemann’s Hypothesis Charaf Ech-Chatbi To cite this version: Charaf Ech-Chatbi. A Short and Simple Proof of the Riemann’s Hypothesis. 2021. hal-03091429v10 HAL Id: hal-03091429 https://hal.archives-ouvertes.fr/hal-03091429v10 Preprint submitted on 5 Mar 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A Short and Simple Proof of the Riemann’s Hypothesis Charaf ECH-CHATBI ∗ Sunday 21 February 2021 Abstract We present a short and simple proof of the Riemann’s Hypothesis (RH) where only undergraduate mathematics is needed. Keywords: Riemann Hypothesis; Zeta function; Prime Numbers; Millennium Problems. MSC2020 Classification: 11Mxx, 11-XX, 26-XX, 30-xx. 1 The Riemann Hypothesis 1.1 The importance of the Riemann Hypothesis The prime number theorem gives us the average distribution of the primes. The Riemann hypothesis tells us about the deviation from the average. Formulated in Riemann’s 1859 paper[1], it asserts that all the ’non-trivial’ zeros of the zeta function are complex numbers with real part 1/2. 1.2 Riemann Zeta Function For a complex number s where ℜ(s) > 1, the Zeta function is defined as the sum of the following series: +∞ 1 ζ(s)= (1) ns n=1 X In his 1859 paper[1], Riemann went further and extended the zeta function ζ(s), by analytical continuation, to an absolutely convergent function in the half plane ℜ(s) > 0, minus a simple pole at s = 1: s +∞ {x} ζ(s)= − s dx (2) s − 1 xs+1 Z1 ∗One Raffles Quay, North Tower Level 35.
    [Show full text]
  • RIEMANN's HYPOTHESIS 1. Gauss There Are 4 Prime Numbers Less
    RIEMANN'S HYPOTHESIS BRIAN CONREY 1. Gauss There are 4 prime numbers less than 10; there are 25 primes less than 100; there are 168 primes less than 1000, and 1229 primes less than 10000. At what rate do the primes thin out? Today we use the notation π(x) to denote the number of primes less than or equal to x; so π(1000) = 168. Carl Friedrich Gauss in an 1849 letter to his former student Encke provided us with the answer to this question. Gauss described his work from 58 years earlier (when he was 15 or 16) where he came to the conclusion that the likelihood of a number n being prime, without knowing anything about it except its size, is 1 : log n Since log 10 = 2:303 ::: the means that about 1 in 16 seven digit numbers are prime and the 100 digit primes are spaced apart by about 230. Gauss came to his conclusion empirically: he kept statistics on how many primes there are in each sequence of 100 numbers all the way up to 3 million or so! He claimed that he could count the primes in a chiliad (a block of 1000) in 15 minutes! Thus we expect that 1 1 1 1 π(N) ≈ + + + ··· + : log 2 log 3 log 4 log N This is within a constant of Z N du li(N) = 0 log u so Gauss' conjecture may be expressed as π(N) = li(N) + E(N) Date: January 27, 2015. 1 2 BRIAN CONREY where E(N) is an error term.
    [Show full text]
  • Zeta Functions and Chaos Audrey Terras October 12, 2009 Abstract: the Zeta Functions of Riemann, Selberg and Ruelle Are Briefly Introduced Along with Some Others
    Zeta Functions and Chaos Audrey Terras October 12, 2009 Abstract: The zeta functions of Riemann, Selberg and Ruelle are briefly introduced along with some others. The Ihara zeta function of a finite graph is our main topic. We consider two determinant formulas for the Ihara zeta, the Riemann hypothesis, and connections with random matrix theory and quantum chaos. 1 Introduction This paper is an expanded version of lectures given at M.S.R.I. in June of 2008. It provides an introduction to various zeta functions emphasizing zeta functions of a finite graph and connections with random matrix theory and quantum chaos. Section 2. Three Zeta Functions For the number theorist, most zeta functions are multiplicative generating functions for something like primes (or prime ideals). The Riemann zeta is the chief example. There are analogous functions arising in other fields such as Selberg’s zeta function of a Riemann surface, Ihara’s zeta function of a finite connected graph. We will consider the Riemann hypothesis for the Ihara zeta function and its connection with expander graphs. Section 3. Ruelle’s zeta function of a Dynamical System, A Determinant Formula, The Graph Prime Number Theorem. The first topic is the Ruelle zeta function which will be shown to be a generalization of the Ihara zeta. A determinant formula is proved for the Ihara zeta function. Then we prove the graph prime number theorem. Section 4. Edge and Path Zeta Functions and their Determinant Formulas, Connections with Quantum Chaos. We define two more zeta functions associated to a finite graph - the edge and path zetas.
    [Show full text]
  • A RIEMANN HYPOTHESIS for CHARACTERISTIC P L-FUNCTIONS
    A RIEMANN HYPOTHESIS FOR CHARACTERISTIC p L-FUNCTIONS DAVID GOSS Abstract. We propose analogs of the classical Generalized Riemann Hypothesis and the Generalized Simplicity Conjecture for the characteristic p L-series associated to function fields over a finite field. These analogs are based on the use of absolute values. Further we use absolute values to give similar reformulations of the classical conjectures (with, perhaps, finitely many exceptional zeroes). We show how both sets of conjectures behave in remarkably similar ways. 1. Introduction The arithmetic of function fields attempts to create a model of classical arithmetic using Drinfeld modules and related constructions such as shtuka, A-modules, τ-sheaves, etc. Let k be one such function field over a finite field Fr and let be a fixed place of k with completion K = k . It is well known that the algebraic closure1 of K is infinite dimensional over K and that,1 moreover, K may have infinitely many distinct extensions of a bounded degree. Thus function fields are inherently \looser" than number fields where the fact that [C: R] = 2 offers considerable restraint. As such, objects of classical number theory may have many different function field analogs. Classifying the different aspects of function field arithmetic is a lengthy job. One finds for instance that there are two distinct analogs of classical L-series. One analog comes from the L-series of Drinfeld modules etc., and is the one of interest here. The other analog arises from the L-series of modular forms on the Drinfeld rigid spaces, (see, for instance, [Go2]).
    [Show full text]
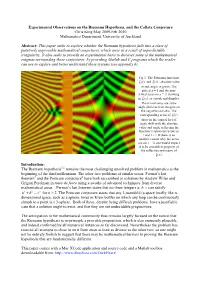
  • Experimental Observations on the Riemann Hypothesis, and the Collatz Conjecture Chris King May 2009-Feb 2010 Mathematics Department, University of Auckland
    Experimental Observations on the Riemann Hypothesis, and the Collatz Conjecture Chris King May 2009-Feb 2010 Mathematics Department, University of Auckland Abstract: This paper seeks to explore whether the Riemann hypothesis falls into a class of putatively unprovable mathematical conjectures, which arise as a result of unpredictable irregularity. It also seeks to provide an experimental basis to discover some of the mathematical enigmas surrounding these conjectures, by providing Matlab and C programs which the reader can use to explore and better understand these systems (see appendix 6). Fig 1: The Riemann functions (z) and (z) : absolute value in red, angle in green. The pole at z = 1 and the non- trivial zeros on x = showing in (z) as a peak and dimples. The trivial zeros are at the angle shifts at even integers on the negative real axis. The corresponding zeros of (z) show in the central foci of angle shift with the absolute value and angle reflecting the function’s symmetry between z and 1 - z. If there is an analytic reason why the zeros are on x = one would expect it to be a manifest property of the reflective symmetry of (z) . Introduction: The Riemann hypothesis1,2 remains the most challenging unsolved problem in mathematics at the beginning of the third millennium. The other two problems of similar status, Fermat’s last theorem3 and the Poincare conjecture4 have both succumbed to solutions by Andrew Wiles and Grigori Perelman in tours de force using a swathe of advanced techniques from diverse mathematical areas. Fermat’s last theorem states that no three integers a, b, c can satisfy an + bn = cn for n > 2.
    [Show full text]
  • Complex Zeros of the Riemann Zeta Function Are on the Critical Line
    December 2020 All Complex Zeros of the Riemann Zeta Function Are on the Critical Line: Two Proofs of the Riemann Hypothesis (°) Roberto Violi (*) Dedicated to the Riemann Hypothesis on the Occasion of its 160th Birthday (°) Keywords: Riemann Hypothesis; Riemann Zeta-Function; Dirichlet Eta-Function; Critical Strip; Zeta Zeros; Prime Number Theorem; Millennium Problems; Dirichlet Series; Generalized Riemann Hypothesis. Mathematics Subject Classification (2010): 11M26, 11M41. (*) Banca d’Italia, Financial Markets and Payment System Department, Rome, via Nazionale 91, Italy. E-Mail: [email protected]. The opinions of this article are those of the author and do not reflect in any way the views or policies of the Banca d’Italia or the Eurosystem of Central Banks. All errors are mine. Abstract In this study I present two independent proofs of the Riemann Hypothesis considered by many the greatest unsolved problem in mathematics. I find that the admissible domain of complex zeros of the Riemann Zeta-Function is the critical line given by 1 ℜ(s) = . The methods and results of this paper are based on well-known theorems 2 on the number of zeros for complex-valued functions (Jensen’s, Titchmarsh’s and Rouché’s theorem), with the Riemann Mapping Theorem acting as a bridge between the Unit Disk on the complex plane and the critical strip. By primarily relying on well- known theorems of complex analysis our approach makes this paper accessible to a relatively wide audience permitting a fast check of its validity. Both proofs do not use any functional equation of the Riemann Zeta-Function, except leveraging its implied symmetry for non-trivial zeros on the critical strip.
    [Show full text]
  • Trivial Zeros of Zeta Functions and Prime Numbers
    A Proof of the Riemann Hypothesis and Determination of the Relationship Between Non- Trivial Zeros of Zeta Functions and Prime Numbers Murad Ahmed Abu Amr MSc Degree in Physics, Mutah University [email protected] ABSTRACT This analysis which uses new mathematical methods aims at proving the Riemann hypothesis and figuring out an approximate base for imaginary non-trivial zeros of zeta function at very large numbers, in order to determine the path that those numbers would take. This analysis will prove that there is a relation links the non-trivial zeros of zeta with the prime numbers, as well as approximately pointing out the shape of this relationship, which is going to be a totally valid one at numbers approaching infinity. Keywords Riemann hypothesis; Zeta function; Non trivial zeros; Prime numbers . INTRODUCTION The Riemann hypothesis states that the real part of every non-trivial zeros of zeta function is always constant and equals ½. The mathematicians hope that the proof of this hypothesis to contribute in defining the locations of prime numbers on the number line. This proof will depend on a new mathematical analysis that is different from the other well-known methods; It`s a series of mathematical steps that concludes a set of mathematical relationships resulted from conducting mathematical analyses concerning Riemann zeta function and Dirichlet eta function after generalizing its form, as I will explain hereinafter, as well as identifying new mathematical functions which I will define its base later. I will resort to this different analysis because the known methods used in separating the arithmetic series to find its zeros cannot figure out the non-trivial zeros of zeta function; besides, I will explain the reason for its lack of success.
    [Show full text]
  • 8. Riemann's Plan for Proving the Prime Number Theorem
    8. RIEMANN'S PLAN FOR PROVING THE PRIME NUMBER THEOREM 8.1. A method to accurately estimate the number of primes. Up to the middle of the nineteenth century, every approach to estimating ¼(x) = #fprimes · xg was relatively direct, based upon elementary number theory and combinatorial principles, or the theory of quadratic forms. In 1859, however, the great geometer Riemann took up the challenge of counting the primes in a very di®erent way. He wrote just one paper that could be called \number theory," but that one short memoir had an impact that has lasted nearly a century and a half, and its ideas have de¯ned the subject we now call analytic number theory. Riemann's memoir described a surprising approach to the problem, an approach using the theory of complex analysis, which was at that time still very much a developing sub- ject.1 This new approach of Riemann seemed to stray far away from the realm in which the original problem lived. However, it has two key features: ² it is a potentially practical way to settle the question once and for all; ² it makes predictions that are similar, though not identical, to the Gauss prediction. Indeed it even suggests a secondary term to compensate for the overcount we saw in the data in the table in section 2.10. Riemann's method is the basis of our main proof of the prime number theorem, and we shall spend this chapter giving a leisurely introduction to the key ideas in it. Let us begin by extracting the key prediction from Riemann's memoir and restating it in entirely elementary language: lcm[1; 2; 3; ¢ ¢ ¢ ; x] is about ex: Using data to test its accuracy we obtain: Nearest integer to x ln(lcm[1; 2; 3; ¢ ¢ ¢ ; x]) Di®erence 100 94 -6 1000 997 -3 10000 10013 13 100000 100052 57 1000000 999587 -413 Riemann's prediction can be expressed precisely and explicitly as p (8.1.1) j log(lcm[1; 2; ¢ ¢ ¢ ; x]) ¡ xj · 2 x(log x)2 for all x ¸ 100: 1Indeed, Riemann's memoir on this number-theoretic problem was a signi¯cant factor in the develop- ment of the theory of analytic functions, notably their global aspects.
    [Show full text]
  • Calculation of Values of L-Functions Associated to Elliptic Curves
    MATHEMATICS OF COMPUTATION Volume 68, Number 227, Pages 1201{1231 S 0025-5718(99)01051-0 Article electronically published on February 10, 1999 CALCULATION OF VALUES OF L-FUNCTIONS ASSOCIATED TO ELLIPTIC CURVES SHIGEKI AKIYAMA AND YOSHIO TANIGAWA Abstract. We calculated numerically the values of L-functions of four typical elliptic curves in the critical strip in the range Im(s) 400. We found that ≤ all the non-trivial zeros in this range lie on the critical line Re(s)=1andare simple except the one at s = 1. The method we employed in this paper is the approximate functional equation with incomplete gamma functions in the coefficients. For incomplete gamma functions, we continued them holomor- phically to the right half plane Re(s) > 0, which enables us to calculate for large Im(s). Furthermore we remark that a relation exists between Sato-Tate conjecture and the generalized Riemann Hypothesis. 1. Introduction and the statement of results The numerical calculations of the Riemann zeta function ζ(s) have a long history. In the critical strip, the Euler-Maclaurin summation formula is applicable, but on the critical line, the famous Riemann-Siegel formula is useful because it is very fast and accurate (see [3] or [8]). Using these formulas, it is known at present that the Riemann Hypothesis holds for Im(s) less than about 1.5 109 (see J. van de Lune, H. J. J. te Riele and D. T. Winter [13]; see also Odlyzko× [16]). By the Euler- Maclaurin summation formula, we can also calculate the values of the Hurwitz zeta function and hence the values of the Dirichlet L-function because it is a finite sum of the Hurwitz zeta functions.
    [Show full text]
  • A Note on the Zeros of Zeta and L-Functions 1
    A NOTE ON THE ZEROS OF ZETA AND L-FUNCTIONS EMANUEL CARNEIRO, VORRAPAN CHANDEE AND MICAH B. MILINOVICH 1 Abstract. Let πS(t) denote the argument of the Riemann zeta-function at the point s = 2 + it. Assuming the Riemann hypothesis, we give a new and simple proof of the sharpest known bound for S(t). We discuss a generalization of this bound (and prove some related results) for a large class of L-functions including those which arise from cuspidal automorphic representations of GL(m) over a number field. 1. Introduction Let ζ(s) denote the Riemann zeta-function and, if t does not correspond to an ordinate of a zero of ζ(s), let 1 S(t) = arg ζ( 1 +it); π 2 where the argument is obtained by continuous variation along straight line segments joining the points 1 2; 2 + it, and 2 + it, starting with the value zero. If t does correspond to an ordinate of a zero of ζ(s), set 1 S(t) = lim S(t+") + S(t−") : 2 "!0 The function S(t) arises naturally when studying the distribution of the nontrivial zeros of the Riemann zeta-function. For t > 0, let N(t) denote the number of zeros ρ = β + iγ of ζ(s) with ordinates satisfying 1 0 < γ ≤ t where any zeros with γ = t are counted with weight 2 . Then, for t ≥ 1, it is known that t t t 7 1 N(t) = log − + + S(t) + O : 2π 2π 2π 8 t In 1924, assuming the Riemann hypothesis, Littlewood [12] proved that log t S(t) = O log log t as t ! 1.
    [Show full text]
  • The Riemann Hypothesis the American Institute of Mathematics
    The Riemann Hypothesis The American Institute of Mathematics This is a hard{copy version of a web page available through http://www.aimath.org Input on this material is welcomed and can be sent to [email protected] Version: Thu Jun 17 05:56:54 2004 This document is a preliminary version of a planned comprehensive resource on the Riemann Hypothesis. Suggestions and contributions are welcome and can be sent to rh(at)aimath.org 1 2 Table of Contents A. What is an L-function? . 4 1. Terminology and basic properties a. Functional equation b. Euler product c. » and Z functions d. Critical line and critical strip e. Trivial zeros f. Zero counting functions 2. Arithmetic L-functions a. The Riemann zeta function b. Dirichlet L-functions c. Dedekind zeta functions d. GL(2) L-functions e. Higher rank L-functions 3. The Selberg class a. Dirichlet series b. Analytic Continuation c. Functional Equation d. Euler Product e. Ramanujan Hypothesis f. Selberg Conjectures 4. Analogues of zeta-functions a. Dynamical zeta-functions b. Spectral zeta functions B. Riemann Hypotheses . 14 1. Riemann Hypotheses for global L-functions a. The Riemann Hypothesis b. The Generalized Riemann Hypothesis c. The Extended Riemann Hypothesis d. The Grand Riemann Hypothesis 2. Other statements about the zeros of L-functions a. Quasi Riemann Hypothesis b. 100 percent hypothesis c. The Density Hypothesis d. Zeros on the σ = 1 line e. Landau-Siegel zeros f. The vertical distribution of zeros 3. The Lindelof hypothesis and breaking convexity 4. Perspectives on RH a. Analytic number theory b.
    [Show full text]