Weather Based Yield Crop Forecasting: Agro-Physics Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Janta Vedic College
Janta Vedic College https://www.indiamart.com/janta-vedic-college/ The college has always been in an expansion mode to meet the increasing demand of vocational education. Industrial Chemistry, Microbiology, Biotechnology and Bioinformatics are recently added self-financed vocational courses. About Us Janta Vedic College Baraut (Affiliated to Chaudhary Charan Singh University Meerut) is a premier institution of North India. It is located in a semi-urban area surrounded by rural area and committed to the education and development of the peasantry. It has been imparting quality education in Arts, Science and Agriculture for over six decades making significant contribution to social, cultural, economical and intellectual development of the community. It is managed and maintained by the Jat Shiksha Sabha a registered society and its parent body. Since its modest beginning as a Vedic High School in 1917, the college now imparts education in 12 subjects at UG level, 17 subjects at PG level and undertakes research in 15 subjects for Ph.D. The college receives regular and special development grants from the UGC and it is well equipped with WI-FI internet connection; INFLIBNET and other modern learning resources. Modern teaching methods are used for class- room teaching. The college has always been in an expansion mode to meet the increasing demand of vocational education. Industrial Chemistry, Microbiology, Biotechnology and Bioinformatics are recently added self-financed vocational courses. For more information, please visit https://www.indiamart.com/janta-vedic-college/aboutus.html Products & Services ) g A ( C S . M c S A . M M G P F a c t s h e e t Year of Establishment : 1917 Nature of Business : Supplier CONTACT US Janta Vedic College Contact Person: Shiv Singh Baraut Baghpat - 250611, Uttar Pradesh, India https://www.indiamart.com/janta-vedic-college/. -

Brijesh Kumar Meena* V. K. Dwivedi Shobhit Kumar Singh KEYWORDS INTERNATIONAL JOURNAL of SCIENTIFIC RESEARCH
ORIGINAL RESEARCH PAPER Volume-8 | Issue-6 | June-2019 | PRINT ISSN No. 2277 - 8179 INTERNATIONAL JOURNAL OF SCIENTIFIC RESEARCH STUDIES ON HERITABILITY AND GENETIC ADVANCE OF INDIAN MUSTARD (BRASSICA JUNCEA L.) Agricultural Science Brijesh Kumar Faculty of Agriculture & Veterinary Science, Mewar University, Chittorgarh, Raj. India Meena* *Corresponding Author V. K. Dwivedi Deptt. of Genetics and Plant Breeding, Janta Vedic College, Baraut (U.P.) India Devendra Kumar Deptt. of Agroforestry, Mewar University, Chittorgarh ,Raj., India Shobhit Kumar Genetics and Plant Breeding, Banaras Hindu University, Varanasi (U.P.) India Singh KEYWORDS INTRODUCTION Heritability and genetics advance are important selection parameters. Rapeseed-mustard (Brassica juncea L.) is the second important Heritability estimates along with genetics advanced are normally more oilseed crop of the country after soybean and plays a very signicant helpful in predicting genetics gain under selection than heritable role in the oil economy by contributing about 30 percent to the total estimates alone (Johnson et al.1955). oilseed production. The genus Brassica mainly includes Brassica juncea, Brassica carinata and Brassica napus as tetraploid species and The correlation coefcient gives an idea about the associations exist Brassica rapa, Brassica nigra and Brassica oleracia as diploid between yield and its components. However, it is a well-known fact species. Brassica juncea is a major winter oil seed crop of India that correlation mainly does not full the purpose because it does not occupying 6.39 m ha with total production of 7.41m tones and average full the purpose because it does not affect the characters having productivity of 1104kg/ha (Anonymous, 2010). -

Annexures for Chapter 2
Annexures for Chapter 2 Annexure-2.1 List of Agricultural Universities in India State Universities Andhra 1. Acharya N.G. Ranga Agricultural University, Pradesh Rajendranagar, Hyderabad-500 030 2. Andhra Pradesh Horticulture University Tadepalligudem, Andhra Pradesh - 534 101 3. Sri Venkateswara Veterinary University Tirupati, Chitor 517 502 Assam 4. Assam Agricultural University Jorhat-785 012, Assam Bihar 5. Bihar Agricultural University Sabour -813 210, Bhagalpur District, Bihar 6. Rajendra Agricultural University Pusa, Samastipur 848 125 , Bihar Chhattisgarh 7. Indira Gandhi Krishi Vishwavidyalaya Raipur 492 012, Chhattisgarh Delhi 8. Indian Agricultural Research Institute, New Delhi 110012 (Deemed Univ) Gujarat 9. Anand Agricultural University Anand 388 110, Gujarat 10. Junagadh Agricultural University Junagadh 362 001, Gujarat 11. Navasari Agricultural University Navsari 396450, Gujarat 12. Sardarkrushinagar – Dantiwada Agricultural University Sardar Krushinagar, District Banaskantha 385 506, Gujarat 13. Kamdhenu University for Veterinary, Dairy Science and Fisheries, Himmatnagar, Sabarkantha-383001, Gujarat* Haryana 14. Ch Charan Singh Haryana Agricultural University Hisar, 125004 Haryana 15. Lala Lajpat Rai University of Veterinary & Animal Sciences, Hisar 125001 Haryana* 16. National Dairy Research Institute, Karnal 132 001 (Deemed Univ) Himachal 17. CSK Himachal Pradesh Krishi Vishvavidyalaya Pradesh Palampur 176 062, Himachal Pradesh 18. Dr Yashwant Singh Parmar University of Agriculture & Forestry Solan, Nauni 173 230, Himachal Pradesh Jammu & 19. Sher-E-Kashmir University of Agricultural Sciences & Technology Kashmir Jammu 180 012, Jammu & Kashmir 20. Sher-E-Kashmir of Agricultural Sciences & Technology of Kashmir Srinagar 191 121, Jammu & Kashmir Jharkhand 21. Birsa Agricultural University Kanke. Ranchi 834 006, Jharkhand Karnataka 22. University of Agricultural Sciences 223 GKVK, Bangalore 560 065 , Karnataka 23. -

A Brief Resume
A Brief Resume Name : ARCHANA SHARMA Address : B-62 Textile Colony Garh Road, Meerut Phone: - 0121-2760173, M. 9319387436 Designation : Professor & Head, Department of Political Science Ch. Charan Singh University, Meerut & Dean Faculty of Arts, Ch. Charan Singh University, Meerut Born : 29.12.1954 Academic Qualifications Exam. Passed Year Board/Uni. Percentage Division High School 1969 U.P. Board, Allahabad 70% First Intermediate 1971 U.P. Board, Allahabad 71% First B.A. 1973 Agra University, Agra 61% First M.A.(Gold Medal) 1975 Agra University, Agra 62% First M.Phil 1978 School of International A Soviet – Vietnamese Studies, J.N.U. Relations 1964-1968 Ph.D. 1989 Department of Politics British Foreign Policy Towards Hull University, U.K. Malasiya 1957-1967 Teaching Experience 1. Joined as a lecturer in the department of Political Science, Ch. Charan Singh University as Permanent lecturer on 30th September, 1977. 2. Joined as a Reader in the Department on 12.02.1992 3. Joined as a Professor in the Department on 8.11.2001 4. Taught both, M.A. since 1977 and M.Phil since 1980. 5. Shall complete 31 years of teaching in the department on 30th September 2008 Research Experience (Self) 1. M.Phil 1975-1978 : S.I.S., J.N.U. – Soviet Vietnamese Relations 1964-1968 2. Ph.D. 1981- 1989 : Department of Politics, Hull University, U.K. British Foreign Policy towards Malasiya 1957-1967 Research Guidance Ph.D. awarded 1. Manmeet Kaur (1991) : Community Transformation and Electoral Participation : A study of Muzaffarnagar City. 2. Km. Madhu Sharma (1993): Pressure Groups in Politics : A study of Meerut University Karamchari Union. -
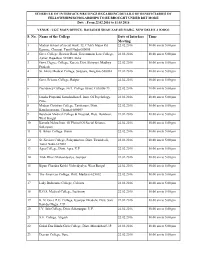
S. No. Name of the College Date of Interface Meeting Time
SCHEDULE OF INTERFACE MEETINGS REGARDING DETAILS OF BENEFICIARIES OF FELLOWSHIPS/SCHOLARSHIPS TO BE BROUGHT UNDER DBT MODE Date : From 22.02.2016 to 11.03.2016 VENUE : UGC MAIN OFFICE. BAHADUR SHAH ZAFAR MARG. NEW DELHI -11OOO2 S. No. Name of the College Date of Interface Time Meeting 1 Madras School of social work, 32, CASA Major Rd, 22.02.2016 10.00 am to 5.00 pm Egmore, Chennai, Tamil Nadu 600008 2 Govt. College, Beawer Road, Government Law College, 22.02.2016 10.00 am to 5.00 pm Ajmer, Rajasthan 305001, India 3 Govt. Degree College, Karera, Dist. Shivpuri, Madhya 22.02.2016 10.00 am to 5.00 pm Pradesh 4 St. John's Medical College, Sarjpura, Banglore-560034 22.02.2016 10.00 am to 5.00 pm 5 Govt. Science College, Raipur 22.02.2016 10.00 am to 5.00 pm 6 Presidency College, 86/1, College Street, Calcutta-73 22.02.2016 10.00 am to 5.00 pm 7 Janaha Prupodni Samshodhan S. Instt. Of Psychology, 22.02.2016 10.00 am to 5.00 pm Pune 8 Madras Christian College, Tambaram, Distt. 22.02.2016 10.00 am to 5.00 pm Kancheepuram, Chennai-600059 9 Burdwan Medical College & Hospital, Distt. Burdwan, 22.02.2016 10.00 am to 5.00 pm West Bengal 10 Kamala Nehru Instt. Of Phsical Of Social Science, 22.02.2016 10.00 am to 5.00 pm Sultanpuri 11 B. Bihari College, Jhansi 22.02.2016 10.00 am to 5.00 pm 12 St. -

Curriculum-Vitae
Curriculum-Vitae Title Dr. First Name NARENDRA Last Name SINGH Photograph Designation Teaching Assistant Department Dept. of Political Science, Ch. Charan Singh University, Meerut Father's Name Shri Jagat Singh Date of Birth 15th July 1981 Address 63/9 Jagrti Vihar, Garh Road, (Residence) Meerut-250004 (U.P.) INDIA Mobile Number +91-9917777999, +91-8077350886 Email [email protected], [email protected] Education Degree Subject Institution Year Details/Grade/Percentage Ph.D. Political Science Ch. Charan Singh University Campus, 2008 Research Degree obtained in the area Meerut of Human Rights on the topic entitled “MANVADHIKAR EVAM MAHILAON KI RAJNAITIK SAHBHAGITA” M. Phil. Political Science Ch. Charan Singh University Campus, 2005 Obtained 66.50% marks Meerut M.A. Sociology Ch. Charan Singh University Campus, 2011 Obtained 61.50% marks Meerut M.Ed. Education Ch. Charan Singh University Campus, 2009 Obtained 68.71% marks Meerut B.Ed. Hindi, Social Ch. Charan Singh University Campus, 2006 Obtained 65.10% marks Sciences Meerut M.A. Political Science Ch. Charan Singh University Campus, 2004 Obtained 67.50% marks Meerut B.A. Hindi, English, Ch. Charan Singh University Campus, 2002 Obtained 50.60% marks Political Science Meerut Additional Education: UGC-NET Education University Grants Commission New Dec. 2014 - Delhi Career Profile Teaching Experience Organization/ Institution Designation Duration Role Department of Political Science, Ch. Teaching Assistant 5th Sept. 2017 to continue. Teaching Charan Singh University, Meerut Department of Political Science, Ch. Guest Lecturer 22nd July 2016 to 4th Sept. Teaching Charan Singh University, Meerut 2017 Department of Political Science, Ch. Guest Lecturer 3rd March 2016 to 30th June Teaching Charan Singh University, Meerut 2016 Department of Political Science, Ch. -

Paper Teplate
Volume-05 ISSN: 2455-3085 (Online) Issue-12 RESEARCH REVIEW International Journal of Multidisciplinary December-2020 www.rrjournals.com[Peer Reviewed Journal] DOI: https://doi.org/10.31305/rrijm.2020.v05.i12.037 Nutrient management in wheat (Triticum aestivum L.) for increase grain yield, nutrient-use efficiency and profitability 1Sandeep Kumar, 2Tejveer Singh Tomar and 3Savita Tomar 1Assistant Professor Agronomy, R. M.P. (PG) college, Gurukul Narsan, Haridwar (Uttarakhand). 2,3Assistant professor Agronomy, Janta Vedic college, Baraut (Baghpat ) U.P. ARTICLE DETAILS ABSTRACT Article History A field experiment was conducted during the winter (Rabi) season 2015-16 at Published Online: 14 December 2020 Agriculture Farm, J. V. Collage Baraut (Baghpat) Uttar Pradesh to study the effect of nutrient management (N.P.K. levels) on growth and yield of wheat (Triticum aestivum Keywords L.). The experiment was a Randomized complete block design with 3 replication and 8 optical sensor, precision nitrogen treatment (control, recommended dose of fertilizer RDF 150 N+60 P205 + 40 K2O management, NDVI, level of nutrients kg/ha), 150% RDF, 150% PK, 150% NK, 150% NP, Green seeker–guided nitrogen recommended dose of fertilizer. application at the 2nd Irrigation P2O5 and RDF+10t FYM/ha: Various yield attributes of wheat showed significant Variation under different levels of NPK and Green seeker- based precision, nutrient management. It was observed that an application of 150% of RDF 225 N + 90 P2O5 + 60 K2O kg/ha) resulted in the highest yield and net return. However Green Seeker-guided nitrogen application saved fertilizer nitrogen (32 kg/ha) without significant reduction in yield than control recommendation of recommended dose of fertilizer in HD 3226 wheat. -

The Meeting of the Expert Committee to Evaluate the Proposals Received
The meeting of the Expert Committee to evaluate the proposals received from the Northern Region for Additional Assistance to Universities and 5500 Colleges already covered under Section 12(B) of the UGC, ACT 1956 and Jubilee Centenary grants to Colleges was held from 29th Feb to 2nd March, 2012. Additional Assistance Haryana Kurukshetra University Sr No Amount Allocated Name of the College 1 D.A.V College for Girls, Jagadhri Road, Yamuna Nagar – 135 24.86 001, Haryana 2 30.11 D.A.V. College, Opp Mahila Aashram, karnal – 132 001 3 Indira Gandhi (PG) Mahila Mahavidyalaya, Kaithal- 136 027, 24.80 Haryana 4 Hindu Girls College, Jagadhri- 135 003 21.33 5 26.28 C.M.K. National Post Graduate Girls College, Sirsa, haryana 6 23.90 Gandhi Memorial National College, Ambala Cantt – 133 001 7 Sanatan Dharama College (Lahore), Ambala Cantt, Haryana- 25.00 133 001 8 R.K.S.D. (PG) College, Kaithal, Haryana 31.24 9 Chhaju Ram Memorial Jat College, Hissar 26.71 10 Guru Nanak Girls College, Santpura, Yamuna Nagar- 135 001, 24.25 Haryana 11 Ch. Ishwar Singh Kanya Mahavidyalay, Dhand Dadwana, 24.78 Kaithal, Haryana 12 Dayanand Mahila Mahavidyalaya, Kurukshetra 23.85 13 25.00 M.D. S.D. Girls College, Ambala City- 134 002 14 20.74 Arya Kanya Mahavidyalaya, Shahabad Markanada - 136135, Dist. Kurukshetra, Haryana 15 Dayanand Post Graduate College, Hissar 25.00 16 23.95 Guru Nanak Khalsa College, Yamuna Nagar- 135 001, Haryana 17 University College, Kurukshetra 24.69 18 D.A.V. College, Ambala City- 134 002 23.20 - 1 - 19 D.A.V. -

CURRICULUM - VITAE ______Dr
CURRICULUM - VITAE _____________________________________________________________________ Dr. Praveen Kumar Department of Zoology, M.Sc., M.Phil., Ph.D., M.A., B. Ed. D.N. College, Meerut NAME DR. PRAVEEN KUMAR DESIGNATION ASSISTANT PROFESSOR FATHER’S NAME LATE SHRI RAM SINGH MOTHER’S NAME SMT. RAJKALI DEVI DATE OF BIRTH 20 APRIL,1975 CORRESPONDANCE DEPARTMENT OF ZOOLOGY, ADDRESS D.N. COLLEGE, MEERUT CONTACT NO 09412833311 09058171122 EMAIL ID [email protected] PERMANENT 87/1 – SARASWATI VIHAR, ADDRESS ROHTA ROAD, MEERUT - 250002 MARTIAL STATUS MARRIED NATIONALITY INDIAN ACADEMIC B. SC. FROM C.C.S. QUALIFICATION UNIVERSITY, MEERUT. M. SC. FROM C.S.S. UNIVERSITY, MEERUT. M. PHIL. IN ZOOLOGY FROM C.C.S. UNIVERSITY, MEERUT. PH. D. IN ZOOLOGY FROM C.C.S. UNIVERSITY, MEERUT. B. ED. FROM C.C.S. UNIVERSITY, MEERUT. M. A. EDUCATION FROM C.C.S. UNIVERSITY, MEERUT. COMPUTER SIX MONTHS DIPLOMA IN PROFECIENCY COMPUTER FROM NBC, MEERUT. Research Work: ❖ I have worked as research scholar during M. Phil. on the topic entitled “Roll of Photoperiod in the Regulation of Seasonality in Brahminy myna (Sturnus pagodarum)” in the Department of Zoology, C.C.S. University, Campus, Meerut. ❖ I have worked as research scholar during Ph. D. on the topic entitled “En Epidemiological Profile of Human Gastrointestinal Parasitic Infection with Reference to Malnutrition in District Meerut” in the Department of Zoology, Meerut College, Meerut. Supervision: ❖ Presently one research scholar doing their Ph. D. under supervision me and he is working as assistant professor and selected through Higher Education Selection Commission, Allahabad. ❖ One research scholar also doing their Ph. D. under supervision me. -

Seasonal Abundance of Ctenocephalides Canis (Curtis)
J. Exp. Zool. India Vol. 18, No. 1, pp. 245-247, 2015 ISSN 0972-0030 SEASONAL ABUNDANCE OF CTENOCEPHALIDES CANIS (CURTIS) Arvind Kumar Department of Zoology, Janta Vedic College, Baraut - 250 611, Baghpat, India. email: [email protected] (Accepted 29 December 2014) ABSTRACT : Surveillance on Ctenocephalides canis was conducted from January 2012 to December2012 in Baraut town of Uttar Pradesh, India. A total of 67 dogs were searched for fleas. The higher positivity of dogs was recorded in the month of March as 100% while lowest in October and November. The highest flea index of 5.4 was recorded in May and lowest in December and January. The male female ratio was 1:5.00 in April and 1:1 in December and January. The analysis of data shows increasing flea prevalence at the onset of summer and minimum in winter. Key words : Seasonal abundance, flea, Ctenocephalides canis. INTRODUCTION with minimum and maximum temperature range from 0 0 Fleas are haematophagous insects belonging to the 02 C and 45 C in winter and summer seasons order Siphonaptera. They are important from the medical respectively. The area is bound by one big river Yamuna point of view, since they transmit a number of pathogens. in the west and two small rivers in the east. The water There are about 200 flea species around the world (Borror, table of the area is approximately 5-10 feet. As mentioned 1981). Some of them cause dreaded diseases like plague earlier that the study was conducted from January 2012 and flea born spotted fever in humans and their pets. -

Faculty Details Page on Web-Site
Curriculum vitae YEAR 2019 - 2020 Name DR SATISH KUMAR Photograph Designation Associate Professor Department Mathematics Address Department of Mathematics, (Campus) D. N. College, Meerut A-9, Nand Vihar, (Residential) Rohta Road, Meerut , 250001 Phone No 0121 -2519222 (Campus) 91-9897621704 (Residence) Optional Mobile 91-9897621704 Fax 0121-4007794 Email [email protected] Web-Page ACADEMIC QUALIFICATIONS : Course Institution Year Details Ph.D. C.C.S. University ,Meerut 2006 Title ; “Cost Benefit Analysis of Non- Markovian Models of Some Redundant Systems” M.Phil. Institute of Advanced Studies, 1990 Title-“Non- Expansive Mappings of Some Fixed Meerut University ,Meerut Point Theorems” M.Sc. Meerut University, Meerut 1989 Mathematics Career Profile S.No. Organization/Institution Designati Duration Role on 1. Govt. PG College, Ranikhet (U.P). Lecturer 23-12-1998 to 05-07- Teaching 1999 2. Govt. PG College, Rishikesh (U.P). Lecturer 05-07-1999 to 22-12- Teaching 1999 3. Janta Vedic College, Baraut, (U.P.) Reader 23-12-1999 to 10-08- Teaching 2010 and Research 4. D. N. College, Meerut, (U.P). Associate 11-08-2010 onwards Teaching & Professor Research Teaching Experience (Subject/Courses Taught ) B.Sc. All Subjects Since 23-12-1998 to till date M.Sc. Advance Algebra(H-1049), Discrete Mathematics(H2051), Since 05-07-1999 to 22-12- Number Theory(H 4049), Advanced Mathematical 1999 and 11-08-2010 to till Methods(H 3051) date. Research Activities III (A) (Detailed of Published Research Papers) S.N. Title Name of Co-authors Name of Journal Refereed / Indexed / ISSN No. / ISBN No. 1. Cost Benefit Analysis Gupta Rakesh, and Proceedings Of National ISBN:81-8283- of Two Dissimilar Agarwal D.C. -

Applied Sciences Humanities
ISSN 0976-1217 S A J H I J.V.C. J .V T .C U . BAR A International Journal of IJASH Applied Sciences and Humanities Volume 2 J.V.C. July 2011-June 2012 Baraut–250611 (Baghpat) U.P. (India) RNI : Registration No. UPMUL/2010/33541 International Journal of Applied Sciences and Humanities JULY 2011-JUNE 2012 Volume 2 Patron : Shri Virendra Pal Singh President Managing Committee, Janta Vedic College Baraut (Baghat) U.P. Editor : Dr. Yeshveer Singh Tomar, Principal, J.V. College, Baraut (Baghpat) U.P. E-mail : [email protected] Editorial Board Dr. Arun K. Mishra, Deptt. of English Dr. Pratap Chaudhary, Deptt. of Political Science Dr. Shyam Kishore, Deptt. of Chemistry Dr. V. K. Dwivedi, Deptt. of Genetics and Plant Breeding Editorial Advisory Board Prof. S.V.S. Rana, Vice Chancellor, Bundelkhand University, Jhansi Prof. Arun Kumar, Former Vice-Chancellor, Pt. D.D.U. University Gorakhpur Dr. R.B. Singh, Delhi School of Economics University of Delhi, Delhi Prof. B. K. Singh, Former Vice Chancellor, C.S.J.M. University, Kanpur Prof. Santosh Satya, RDAT, ITT, New Delhi Dr. S.K. Dhaka, University of Delhi, Delhi Prof. Sanjeev K. Sharma, C.C.S. University, Meerut Prof. Y. Vimla, C.C.S. University, Meerut Prof. Y. Shibagaki, Osaka Electro-Communication University, Japan Prof. K. P. Singh, School of Public Health, UNT Health Science Centre at Foot Worth (U.S.A.) Prof. Sudhir Panwar, Lucknow University, Lucknow Dr. Lavanya M. Ramaniah, HPPD, BARC, Mumbai Prof. Pashupati Jha, IIT, Roorkee Dr. G.R. Sahay, Tata Institute of Social Sciences, Mumbai Dr.