DOCSLIB.ORG

Models and Algorithms Under Asymmetric Read and Write Costs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Models and Algorithms Under Asymmetric Read and Write Costs Models and Algorithms under Asymmetric Read and Write Costs Guy E. Blelloch*, Jeremy T. Finemany, Phillip B. Gibbons*, Yan Gu* and Julian Shunz *Carnegie Mellon University yGeorgetown University zU.C. Berkeley Abstract—In several emerging non-volatile technologies for main memory Thus the Q metric may be more relevant in practice, as it focuses on (NVRAM) the cost of reading is significantly cheaper than the cost of reads and writes to the last relevant level of the memory hierarchy. writing. Such asymmetry in memory costs leads to a desire for “write- We use a parameter ! to account for the higher cost of writes so that efficient” algorithms that minimize the number of writes to the NVRAM. While several prior works have explored write-efficient algorithms for we can study the dependence of algorithms on the gap between writes databases or for the unique properties of NAND Flash, our ongoing work and reads. We view ! as being significantly larger than 1, as factors seeks to develop a broader theory of algorithm design for asymmetric up to 1–2 orders of magnitude have been reported in the literature memories. This talk will highlight our recent progress on models, (see [1] and the references therein). algorithms, and lower bounds for asymmetric memories [1], [2], [3]. We extend the classic RAM model to the asymmetric case by defining the Prior work focusing on asymmetric read and write costs for non- (M; !)-ARAM, which consists of a large asymmetric memory and a volatile memory has explored system issues (e.g., [5]), database much smaller symmetric memory of size M, both random access, such that for the asymmetric memory, writes cost ! > 1 times more than algorithms (e.g., [6]) or the unique properties of NAND Flash (e.g., reads. We present algorithms for search trees, priority queues, sorting, [7]) such as its limited endurance and large erase operation. dynamic programming, BFS- and DFS-related graph algorithms, and shortest paths. We also present novel lower bounds for several problems II. NEW ALGORITHMS AND LOWER BOUNDS that reveal fundamental limits on obtaining write-efficient algorithms for these problems. Finally, we propose and study models for asymmetric memories that consider block transfers and/or parallel processing. Search Trees and Priority Queues. We consider the efficiency of balanced binary search trees on the (M; !)-ARAM. Red-black trees I. INTRODUCTION with appropriate rebalancing rules require only O(1) amortized time per update (insertion or deletion) once the location for the key is found. Fifty years of algorithms research has focused on settings in which For a tree of size n, finding a key’s location uses O(log n) reads reads and writes (to memory) have similar cost. But what if reads and but no writes, so the total amortized cost is Q = T = O(! + log n) writes to memory have significantly different costs? How would that per update. Since priority queues can be implemented with a binary impact algorithm design? What is the correct model to measure the search tree, insertion and delete-min have the same bounds. Note that cost of an algorithm on such memories? These questions are coming these good bounds are obtained even for M = O(1). to the fore with the arrival of new non-volatile memory technologies, Sorting. Many classic sorting algorithms like quicksort and merge- such as phase-change memory (PCM), spin-torque transfer magnetic sort require Θ(n log n) reads and writes, and hence would cost RAM (STT-RAM), and memristor-based resistive RAM (ReRAM), O(!n log n) on the (M; !)-ARAM. However, it is well known which have the property that the cost of reading is significantly cheaper that sorting can be implemented by first inserting each key into than the cost of writing, in terms of lower energy, lower latency, and a balanced search tree, and then in-order traversing the tree to write higher (per-module) bandwidth. Such memories will appear in the out the final sorted order. Using the above-mentioned binary search marketplace in the first half of 2016 [4] as a block device, and after tree, the sorting algorithm based on this method requires only O(n) that as a DIMM off the processor’s memory bus. writes with no increase in reads (O(n log n)). This algorithm is This talk highlights our recent results [1], [2], [3] providing a first asymptotically optimal, since comparison sorting n element requires at step towards answering these fundamental questions about asymmetric least Ω(n log n) comparisons and n writes are necessary to produce memories. We introduce a simple model for studying such memories, the sorted output in contiguous memory. On the (M; !)-ARAM, and a number of new results. Q = T = O(n log n + !n), even for M = O(1). Definition 1: We define the (M; !)-Asymmetric RAM (ARAM), com- It is also interesting to consider sorting in parallel on a shared- prised of a symmetric small-memory of size M, an asymmetric memory multicore. In [1] we discussed a parallel version of the large-memory of unbounded size, and an integer write cost !. The sorting algorithm, which has asymptotically the same numbers of ARAM cost Q is the number of reads from large-memory plus ! reads and writes as the above sequential version. The algorithm is times the number of writes to large-memory. The time T is Q plus highly parallel, with a critical path length of only O(! log n). the number of reads and writes to small-memory. Dynamic Programming. With regards to dynamic programming, We focus on settings in which the problem input fits in the large- some problems are reasonably easy and some harder. The standard memory (and hence can be viewed as “unbounded” size) but not in Floyd-Warshal algorithm for the all-pairs shortest-path (APSP) prob- the small-memory (i.e., M n, where n is the input size and M is lem uses O(n3) writes, and hence would cost Q = T = O(!n3). measured in units of the size of an input item). The large-memory Kleene’s divide-and-conquer algorithm can be used to reduce the models the NVRAM, while the small-memory models either DRAM, ARAM cost. Each recursive call makes two calls to itself on problems if present, or cache memory. The time T extends the time complexity of half the size, and six calls to matrix multiply over the semiring on a RAM model to the asymmetric setting. The cost Q accounts (min; +). Here we analyze the algorithm in the (M; !)-ARAM. The for just the data transfers between the small-memory and the large- matrix multiplies on two matrices of sizep n × n can be done in 2 memory, charging ! for each write and 1 for each read. While T has the model in QM (n) = O(n (! + n= M)) [1]. This leads to 2 the advantage of being most similar to the RAM model, it hides the the recurrence QKleene(n) = 2QKleene(n=2)+O(QM (n))+O(!n ), performance gap between different levels of the memory hierarchy. which solves to QKleene(n) = O(QM (n)) since the cost is dominated at the root of the recurrence. This is a factor of n fewer writes than the RAM results, for which the two have the same asymptotic complexity. Floyd-Warshal algorithm. A similar approach can be used for several other problems, including sequence alignment with gaps, optimal III. OTHER MODELS AND RESULTS binary search trees, and matrix chain multiplication [2]. “External” memory sorting. We considered explicitly modeling the Longest common subsequence and Edit distance are more challenging. transfer of data between the two memories in units of size B > 1. If the answer is directly computed using the classic recursion formula- We adapt the well-studied External Memory model (a.k.a., the I/O tion, the dependency structure of the computation is a diamond DAG, model or the Disk model used in databases) to charge ! times more whose properties have been well-studied in the symmetric memory for writing a block of size B to the asymmetric memory than for setting. For our asymmetric setting, we proved a new lower bound reading such a block. We examine the three general approaches for showing that the ARAM cost Q cannot be asymptotically reduced for sorting on the External Memory model—multi-way mergesort, sample the diamond DAG, even when only selectively storing intermediate sort, and buffer-tree sort—and showed that each of these algorithms values of the diamond DAG and allowing for recomputation of partial can be adapted to use fewer writes. Interestingly, each of the original results—well-known techniques for reducing the number of writes. algorithms have the same optimal cost on the External Memory model, To overcome this fundamental limitation, we must violate the classic and we show that each can be adapted to the asymmetric setting to evaluation method for a DAG that requires a node’s execution must have the same Q = O(!n=B log!M=B (n=B)) cost. While the new wait until all its immediate predecessors in the DAG have executed. multi-way mergesort algorithm is similar to prior work [6] and the Instead, we show a new approach that performs partial accumulation new samplesort algorithm is readily achieved, the new buffer-tree sort at a node based on values computed at only some of its predecessors requires a number of new techniques [1]. at a time, combined with selective recomputations, which overcomes this lower bound. Using this new technique, called a “path sketch”, Cache models.
Load more

Recommended publications
  • Overview of Sorting Algorithms
    Unit 7 Sorting Algorithms Simple Sorting algorithms Quicksort Improving Quicksort Overview of Sorting Algorithms Given a collection of items we want to arrange them in an increasing or decreasing order. You probably have seen a number of sorting algorithms including ¾ selection sort ¾ insertion sort ¾ bubble sort ¾ quicksort ¾ tree sort using BST's In terms of efficiency: ¾ average complexity of the first three is O(n2) ¾ average complexity of quicksort and tree sort is O(n lg n) ¾ but its worst case is still O(n2) which is not acceptable In this section, we ¾ review insertion, selection and bubble sort ¾ discuss quicksort and its average/worst case analysis ¾ show how to eliminate tail recursion ¾ present another sorting algorithm called heapsort Unit 7- Sorting Algorithms 2 Selection Sort Assume that data ¾ are integers ¾ are stored in an array, from 0 to size-1 ¾ sorting is in ascending order Algorithm for i=0 to size-1 do x = location with smallest value in locations i to size-1 swap data[i] and data[x] end Complexity If array has n items, i-th step will perform n-i operations First step performs n operations second step does n-1 operations ... last step performs 1 operatio. Total cost : n + (n-1) +(n-2) + ... + 2 + 1 = n*(n+1)/2 . Algorithm is O(n2). Unit 7- Sorting Algorithms 3 Insertion Sort Algorithm for i = 0 to size-1 do temp = data[i] x = first location from 0 to i with a value greater or equal to temp shift all values from x to i-1 one location forwards data[x] = temp end Complexity Interesting operations: comparison and shift i-th step performs i comparison and shift operations Total cost : 1 + 2 + ..
    [Show full text]
  • The Analysis and Synthesis of a Parallel Sorting Engine Redacted for Privacy Abstract Approv, John M
    AN ABSTRACT OF THE THESIS OF Byoungchul Ahn for the degree of Doctor of Philosophy in Electrical and Computer Engineering, presented on May 3. 1989. Title: The Analysis and Synthesis of a Parallel Sorting Engine Redacted for Privacy Abstract approv, John M. Murray / Thisthesisisconcerned withthe development of a unique parallelsort-mergesystemsuitablefor implementationinVLSI. Two new sorting subsystems, a high performance VLSI sorter and a four-waymerger,werealsorealizedduringthedevelopment process. In addition, the analysis of several existing parallel sorting architectures and algorithms was carried out. Algorithmic time complexity, VLSI processor performance, and chiparearequirementsfortheexistingsortingsystemswere evaluated.The rebound sorting algorithm was determined to be the mostefficientamongthoseconsidered. The reboundsorter algorithm was implementedinhardware asasystolicarraywith external expansion capability. The second phase of the research involved analyzing several parallel merge algorithms andtheirbuffer management schemes. The dominant considerations for this phase of the research were the achievement of minimum VLSI chiparea,design complexity, and logicdelay. Itwasdeterminedthattheproposedmerger architecture could be implemented inseveral ways. Selecting the appropriate microarchitecture for the merger, given the constraints of chip area and performance, was the major problem.The tradeoffs associated with this process are outlined. Finally,apipelinedsort-merge system was implementedin VLSI by combining a rebound sorter
    [Show full text]
  • Sorting Algorithms Correcness, Complexity and Other Properties
    Sorting Algorithms Correcness, Complexity and other Properties Joshua Knowles School of Computer Science The University of Manchester COMP26912 - Week 9 LF17, April 1 2011 The Importance of Sorting Important because • Fundamental to organizing data • Principles of good algorithm design (correctness and efficiency) can be appreciated in the methods developed for this simple (to state) task. Sorting Algorithms 2 LF17, April 1 2011 Every algorithms book has a large section on Sorting... Sorting Algorithms 3 LF17, April 1 2011 ...On the Other Hand • Progress in computer speed and memory has reduced the practical importance of (further developments in) sorting • quicksort() is often an adequate answer in many applications However, you still need to know your way (a little) around the the key sorting algorithms Sorting Algorithms 4 LF17, April 1 2011 Overview What you should learn about sorting (what is examinable) • Definition of sorting. Correctness of sorting algorithms • How the following work: Bubble sort, Insertion sort, Selection sort, Quicksort, Merge sort, Heap sort, Bucket sort, Radix sort • Main properties of those algorithms • How to reason about complexity — worst case and special cases Covered in: the course book; labs; this lecture; wikipedia; wider reading Sorting Algorithms 5 LF17, April 1 2011 Relevant Pages of the Course Book Selection sort: 97 (very short description only) Insertion sort: 98 (very short) Merge sort: 219–224 (pages on multi-way merge not needed) Heap sort: 100–106 and 107–111 Quicksort: 234–238 Bucket sort: 241–242 Radix sort: 242–243 Lower bound on sorting 239–240 Practical issues, 244 Some of the exercise on pp.
    [Show full text]
  • An Evolutionary Approach for Sorting Algorithms
    ORIENTAL JOURNAL OF ISSN: 0974-6471 COMPUTER SCIENCE & TECHNOLOGY December 2014, An International Open Free Access, Peer Reviewed Research Journal Vol. 7, No. (3): Published By: Oriental Scientific Publishing Co., India. Pgs. 369-376 www.computerscijournal.org Root to Fruit (2): An Evolutionary Approach for Sorting Algorithms PRAMOD KADAM AND Sachin KADAM BVDU, IMED, Pune, India. (Received: November 10, 2014; Accepted: December 20, 2014) ABstract This paper continues the earlier thought of evolutionary study of sorting problem and sorting algorithms (Root to Fruit (1): An Evolutionary Study of Sorting Problem) [1]and concluded with the chronological list of early pioneers of sorting problem or algorithms. Latter in the study graphical method has been used to present an evolution of sorting problem and sorting algorithm on the time line. Key words: Evolutionary study of sorting, History of sorting Early Sorting algorithms, list of inventors for sorting. IntroDUCTION name and their contribution may skipped from the study. Therefore readers have all the rights to In spite of plentiful literature and research extent this study with the valid proofs. Ultimately in sorting algorithmic domain there is mess our objective behind this research is very much found in documentation as far as credential clear, that to provide strength to the evolutionary concern2. Perhaps this problem found due to lack study of sorting algorithms and shift towards a good of coordination and unavailability of common knowledge base to preserve work of our forebear platform or knowledge base in the same domain. for upcoming generation. Otherwise coming Evolutionary study of sorting algorithm or sorting generation could receive hardly information about problem is foundation of futuristic knowledge sorting problems and syllabi may restrict with some base for sorting problem domain1.
    [Show full text]
  • Sorting Partnership Unless You Sign Up! Brian Curless • Homework #5 Will Be Ready After Class, Spring 2008 Due in a Week
    Announcements (5/9/08) • Project 3 is now assigned. CSE 326: Data Structures • Partnerships due by 3pm – We will not assume you are in a Sorting partnership unless you sign up! Brian Curless • Homework #5 will be ready after class, Spring 2008 due in a week. • Reading for this lecture: Chapter 7. 2 Sorting Consistent Ordering • Input – an array A of data records • The comparison function must provide a – a key value in each data record consistent ordering on the set of possible keys – You can compare any two keys and get back an – a comparison function which imposes a indication of a < b, a > b, or a = b (trichotomy) consistent ordering on the keys – The comparison functions must be consistent • Output • If compare(a,b) says a<b, then compare(b,a) must say b>a • If says a=b, then must say b=a – reorganize the elements of A such that compare(a,b) compare(b,a) • If compare(a,b) says a=b, then equals(a,b) and equals(b,a) • For any i and j, if i < j then A[i] ≤ A[j] must say a=b 3 4 Why Sort? Space • How much space does the sorting • Allows binary search of an N-element algorithm require in order to sort the array in O(log N) time collection of items? • Allows O(1) time access to kth largest – Is copying needed? element in the array for any k • In-place sorting algorithms: no copying or • Sorting algorithms are among the most at most O(1) additional temp space.
    [Show full text]
  • Meant to Provoke Thought Regarding the Current "Software Crisis" at the Time
    1 www.onlineeducation.bharatsevaksamaj.net www.bssskillmission.in DATA STRUCTURES Topic Objective: At the end of this topic student will be able to: At the end of this topic student will be able to: Learn about software engineering principles Discover what an algorithm is and explore problem-solving techniques Become aware of structured design and object-oriented design programming methodologies Learn about classes Learn about private, protected, and public members of a class Explore how classes are implemented Become aware of Unified Modeling Language (UML) notation Examine constructors and destructors Learn about the abstract data type (ADT) Explore how classes are used to implement ADT Definition/Overview: Software engineering is the application of a systematic, disciplined, quantifiable approach to the development, operation, and maintenance of software, and the study of these approaches. That is the application of engineering to software. The term software engineering first appeared in the 1968 NATO Software Engineering Conference and WWW.BSSVE.INwas meant to provoke thought regarding the current "software crisis" at the time. Since then, it has continued as a profession and field of study dedicated to creating software that is of higher quality, cheaper, maintainable, and quicker to build. Since the field is still relatively young compared to its sister fields of engineering, there is still much work and debate around what software engineering actually is, and if it deserves the title engineering. It has grown organically out of the limitations of viewing software as just programming. Software development is a term sometimes preferred by practitioners in the industry who view software engineering as too heavy-handed and constrictive to the malleable process of creating software.
    [Show full text]
  • Evaluation of Sorting Algorithms, Mathematical and Empirical Analysis of Sorting Algorithms
    International Journal of Scientific & Engineering Research Volume 8, Issue 5, May-2017 86 ISSN 2229-5518 Evaluation of Sorting Algorithms, Mathematical and Empirical Analysis of sorting Algorithms Sapram Choudaiah P Chandu Chowdary M Kavitha ABSTRACT:Sorting is an important data structure in many real life applications. A number of sorting algorithms are in existence till date. This paper continues the earlier thought of evolutionary study of sorting problem and sorting algorithms concluded with the chronological list of early pioneers of sorting problem or algorithms. Latter in the study graphical method has been used to present an evolution of sorting problem and sorting algorithm on the time line. An extensive analysis has been done compared with the traditional mathematical methods of ―Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort. Observations have been obtained on comparing with the existing approaches of All Sorts. An “Empirical Analysis” consists of rigorous complexity analysis by various sorting algorithms, in which comparison and real swapping of all the variables are calculatedAll algorithms were tested on random data of various ranges from small to large. It is an attempt to compare the performance of various sorting algorithm, with the aim of comparing their speed when sorting an integer inputs.The empirical data obtained by using the program reveals that Quick sort algorithm is fastest and Bubble sort is slowest. Keywords: Bubble Sort, Insertion sort, Quick Sort, Merge Sort, Selection Sort, Heap Sort,CPU Time. Introduction In spite of plentiful literature and research in more dimension to student for thinking4. Whereas, sorting algorithmic domain there is mess found in this thinking become a mark of respect to all our documentation as far as credential concern2.
    [Show full text]
  • 10 Sorting, Performance/Stress Tests
    Exercise Set 10 c 2006 Felleisen, Proulx, et. al. 10 Sorting, Performance/Stress Tests In this problem set you will examine the properties of the different algo- rithms we have seen as well as see and design new ones. The goal is to learn to understand the tradeoffs between different ways of writing the same program, and to learn some techniques that can be used to explore the algorithm behavior. Etudes: Sorting Algorithms To practice working with the ArrayList start by implementing the selection sort. Because we will work with several different sorting algorithms, yet want all of them to look the same the selection sort will be a method in the class that extends the abstract class ASortAlgo. A sorting algorithms needs to be given the data to sort, the Comparator to use to determine the ordering, and needs to provide an access to the data it produces. Additionally, the ASort class also includes a field that represents the name of the implement- ing sorting algorithm. abstract class ASortAlgo<T> { /∗∗ the comparator that determines the ordering of the elements ∗/ public Comparator<T> comp; /∗∗ the name of this sorting algorithm ∗/ public String algoName; /∗∗ ∗ Initialize a data set to be sorted ∗ with the data generated by the traversal. ∗ @param the given traversal ∗/ abstract public void initData(Traversal<T> tr); /∗∗ ∗ Sort the data set with respect to the given Comparator ∗ and produce a traversal for the sorted data. ∗ @return the traversal for the sorted data ∗/ abstract public Traversal<T> sort(); } 1 c 2006 Felleisen, Proulx, et. al. Exercise Set 10 1. Design the class ArrSortSelection that implements a selection sort and extends the class ASortAlgo using an ArrayList as the dataset to sort.
    [Show full text]
  • Comparison Sorts Name Best Average Worst Memory Stable Method Other Notes Quicksort Is Usually Done in Place with O(Log N) Stack Space
    Comparison sorts Name Best Average Worst Memory Stable Method Other notes Quicksort is usually done in place with O(log n) stack space. Most implementations on typical in- are unstable, as stable average, worst place sort in-place partitioning is case is ; is not more complex. Naïve Quicksort Sedgewick stable; Partitioning variants use an O(n) variation is stable space array to store the worst versions partition. Quicksort case exist variant using three-way (fat) partitioning takes O(n) comparisons when sorting an array of equal keys. Highly parallelizable (up to O(log n) using the Three Hungarian's Algorithmor, more Merge sort worst case Yes Merging practically, Cole's parallel merge sort) for processing large amounts of data. Can be implemented as In-place merge sort — — Yes Merging a stable sort based on stable in-place merging. Heapsort No Selection O(n + d) where d is the Insertion sort Yes Insertion number of inversions. Introsort No Partitioning Used in several STL Comparison sorts Name Best Average Worst Memory Stable Method Other notes & Selection implementations. Stable with O(n) extra Selection sort No Selection space, for example using lists. Makes n comparisons Insertion & Timsort Yes when the data is already Merging sorted or reverse sorted. Makes n comparisons Cubesort Yes Insertion when the data is already sorted or reverse sorted. Small code size, no use Depends on gap of call stack, reasonably sequence; fast, useful where Shell sort or best known is No Insertion memory is at a premium such as embedded and older mainframe applications. Bubble sort Yes Exchanging Tiny code size.
    [Show full text]
  • Efficient Algorithms and Data Structures for Massive Data Sets
    Efficient Algorithms and Data Structures for Massive Data Sets A Thesis Submitted in Partial Fulfilment of the Requirements for the Degree of Doctor of Philosophy by Alka arXiv:1005.3473v1 [cs.DS] 19 May 2010 Department of Computer Science and Engineering Indian Institute of Technology Guwahati March 2010. ii CERTIFICATE It is certified that the work contained in the thesis entitled Efficient Algorithms and Data Structures for Massive Data Sets by Alka, has been carried out under my supervision and that this work has not been submitted elsewhere for a degree. Dr. Sajith Gopalan Associate Professor Department of Computer Science and Engineering Indian Institute of Technology, Guwahati. March 2010. i ii Abstract For many algorithmic problems, traditional algorithms that optimise on the number of instructions executed prove expensive on I/Os. Novel and very different design techniques, when applied to these problems, can produce algorithms that are I/O efficient. This thesis adds to the growing chorus of such results. The computational models we use are the external memory model and the W-Stream model. On the external memory model, we obtain the following results. (1) An I/O efficient algorithm for computing minimum spanning trees of graphs that improves on the perfor- mance of the best known algorithm. (2) The first external memory version of soft heap, an approximate meldable priority queue. (3) Hard heap, the first meldable external memory priority queue that matches the amortised I/O performance of the known external mem- ory priority queues, while allowing a meld operation at the same amortised cost. (4) I/O efficient exact, approximate and randomised algorithms for the minimum cut problem, which has not been explored before on the external memory model.
    [Show full text]
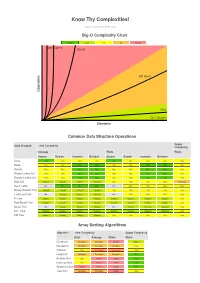
  • Big-O Algorithm Complexity Cheat Sheet
    Know Thy Complexities! www.bigocheatsheet.com Big-O Complexity Chart Excellent Good Fair Bad Horrible O(n!) O(2^n) O(n^2) s O(n log n) n o i t a r e p O O(n) O(1), O(log n) Elements Common Data Structure Operations Space Data Structure Time Complexity Complexity Average Worst Worst Access Search Insertion Deletion Access Search Insertion Deletion Array O(1) O(n) O(n) O(n) O(1) O(n) O(n) O(n) O(n) Stack O(n) O(n) O(1) O(1) O(n) O(n) O(1) O(1) O(n) Queue O(n) O(n) O(1) O(1) O(n) O(n) O(1) O(1) O(n) Singly-Linked List O(n) O(n) O(1) O(1) O(n) O(n) O(1) O(1) O(n) Doubly-Linked List O(n) O(n) O(1) O(1) O(n) O(n) O(1) O(1) O(n) Skip List O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(n) O(n) O(n) O(n) O(n log(n)) Hash Table N/A O(1) O(1) O(1) N/A O(n) O(n) O(n) O(n) Binary Search Tree O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(n) O(n) O(n) O(n) O(n) Cartesian Tree N/A O(log(n)) O(log(n)) O(log(n)) N/A O(n) O(n) O(n) O(n) B-Tree O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(n) Red-Black Tree O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(n) Splay Tree N/A O(log(n)) O(log(n)) O(log(n)) N/A O(log(n)) O(log(n)) O(log(n)) O(n) AVL Tree O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(n) KD Tree O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(n) O(n) O(n) O(n) O(n) Array Sorting Algorithms Algorithm Time Complexity Space Complexity Best Average Worst Worst Quicksort O(n log(n)) O(n log(n)) O(n^2) O(log(n)) Mergesort O(n log(n)) O(n log(n)) O(n log(n)) O(n)
    [Show full text]
  • Studies on Sorting Networks and Expanders
    I STUDIES ON SORTING NETWORKS AND EXPANDERS A Thesis Presented to The Faculty of the School of Electrical Engineering and Computer Science and Fritz J. and Dolores H. Russ College of Engineering and Technology Ohio University In Partial Fulfillment of the Requirement for the Degree Master of Science Hang Xie August, 1998 Acknowledgment I would like to express my special thanks to my advisor, Dr. David W. Juedes, for the insights he has provided to accomplish this thesis and the guidance given to me. Without this, it is impossible for me to accomplish this thesis. I would like to thank Dr. Dennis Irwin, Dr. Gene Kaufman, and Dr. Liming Cai for agreeing to be members of my thesis committee and giving valuable suggestions. I would also like to thank Mr. Dana Carroll for taking time to review my thesis. Finally, I would like to thank my wife and family for the help, support, and encouragement. Contents 1 Introduction 1 1.1 Sorting Networks ..... 2 1.2 Contributions . ..... 5 1.3 Structure of this Thesis .. 6 2 Expander Graphs and Related Constructions 8 2.1 Expander Graphs .... 8 2.2 Explicit Constructions 12 3 The Construction of e -halvers 16 3.1 e-halvers . ....... 17 3.2 Matching ..... 20 3.3 Explicit Construction .. ...... 24 4 Separators 31 4.1 (,x, f, fO)- separators ........ 31 4.2 Construction of the New Separator 34 4.3 Parameter of the New Separator .. ..... 36 ii 5 Paterson's Algorithm 39 5.1 A Tree-sort Metaphor . ........ ...... 40 5.2 The Parameters and Constraints. 41 5.3 On the Boundary ....
    [Show full text]