Diffcoeff a Latex Package to Ease the Writing of Differential Coefficients In
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DCSA API Design Principles 1.0
DCSA API Design Principles 1.0 September 2020 Table of contents Change history ___________________________________________________ 4 Terms, acronyms, and abbreviations _____________________________________ 4 1 Introduction __________________________________________________ 5 1.1 Purpose and scope ________________________________________________ 5 1.2 API characteristics ________________________________________________ 5 1.3 Conventions ____________________________________________________ 6 2 Suitable _____________________________________________________ 6 3 Maintainable __________________________________________________ 6 3.1 JSON _________________________________________________________ 6 3.2 URLs __________________________________________________________ 6 3.3 Collections _____________________________________________________ 6 3.4 Sorting ________________________________________________________ 6 3.5 Pagination______________________________________________________ 7 3.6 Property names __________________________________________________ 8 3.7 Enum values ____________________________________________________ 9 3.8 Arrays _________________________________________________________ 9 3.9 Date and Time properties ___________________________________________ 9 3.10UTF-8 _________________________________________________________ 9 3.11 Query parameters _______________________________________________ 10 3.12 Custom headers ________________________________________________ 10 3.13 Binary data _____________________________________________________ 11 -

The IHO S-100 Standard and E-Navigation Information
e-NAV10/INF/7 e-NAV10 Information paper Agenda item 12 Task Number Author(s) Raphael Malyankar, Jeppesen Jarle Hauge, Norwegian Coastal Administration The IHO S-100 Standard and e-Navigation Information Concept Exploration with Ship Reporting Data and Product Specification 1 SUMMARY The papers describe an exploration in modeling substantially non-geographic maritime information using the S-100 framework, specifically notice of arrival and pilot requests in Norway. The Norwegian Coastal Administration is the National Competent Authority for the European SafeSeaNet (SSN) in Norway and thereby maintains a vessel and voyage reporting system intended for use by commercial marine traffic arriving and departing Norwegian ports. Data used in this system describes vessels, HAZMAT cargo, voyages, and information used in arranging pilotage. Jeppesen and the NCA has developed a product specification (the “NOAPR product specification”) based on the S-100 standard, for a subset of information used in the abovementioned system. The product specification describes the data model for ship reporting and pilot requests. The current version is a “proof-of-concept” intended to explore the development of S-100 compatible data models for non-geographic maritime information. The papers also discuss the use of the Geospatial Information Registry and the NOAPR Model. 1.1 Purpose of the document The product specification [NOAPR] demonstrates the feasibility of modelling ship notice of arrival and pilot requests using the data model compatible with S-100. 2 BACKGROUND The papers are a result of a mutual work between Jeppesen and the Norwegian Coastal Administration within the Interreg project; BLAST (http://www.blast-project.eu/index.php). -

AP Style Style Versus Rules
Mignon Fogarty AP Style Style Versus Rules AP Style Why the AP Stylebook? AP Style What are the key differences in AP style? AP Style AP Style — Does not use italics. AP Style No Italics This means most titles go in quotation marks. AP Style Quotation Marks “Atomic Habits” (book) “Candy Crush”(computer game) “Jumanji” (movie) + opera titles, poem titles, album titles, song titles, TV show titles, and more AP Style No Quotation Marks — Holy Books (the Bible, the Quran) — Reference Books (Webster’s New World College Dictionary, Garner’s Modern English Usage) AP Style No Quotation Marks — Newspaper and Magazine Names (The Washington Post, Reader’s Digest) — Website and App Names (Yelp, Facebook) — Board Games (Risk, Settlers of Catan) AP Style Quotation Marks — Billy waited 30 seconds for “Magic the Gathering” to launch on his iPad. — The boys meet every Saturday at the game store to play Magic the Gathering. AP Style AP Style — Does not use italics. — Doesn’t always use the serial comma. AP Style Serial Comma red, white, and blue AP Style AP Style red, white and blue AP Style Serial Comma Do use it when series elements contain conjunctions. AP Style Serial Comma — Peanut butter and jelly — Ham and eggs — Macaroni and cheese AP Style AP Style I like peanut butter and jelly, ham and eggs, and macaroni and cheese. AP Style AP Style I like peanut butter and jelly, ham, and cheese. AP Style Serial Comma Do use it when series elements contain complex phrases. AP Style AP Style Squiggly wondered whether Aardvark had caught any fish, whether Aardvark would be home for dinner, and whether Aardvark would be in a good mood. -

Abbreviation with Capital Letters
Abbreviation With Capital Letters orSometimes relativize beneficentinconsequentially. Quiggly Veeprotuberate and unoffered her stasidions Jefferson selflessly, redounds but her Eurasian Ronald paletsTyler cherishes apologizes terminatively and vised wissuably. aguishly. Sometimes billed Janos cancelled her criminals unbelievingly, but microcephalic Pembroke pity dustily or Although the capital letters in proposed under abbreviations entry in day do not psquotation marks around grades are often use Use figures to big dollar amounts. It is acceptable to secure the acronym CPS in subsequent references. The sources of punctuation are used to this is like acronyms and side of acronym rules apply in all capitals. Two words, no bag, no hyphen. Capitalize the months in all uses. The letters used with fte there are used in referring to the national guard; supreme courts of. As another noun or recognize: one are, no hyphen, not capitalized. Capitalize as be would land the front porch an envelope. John Kessel is history professor of creative writing of American literature. It introduces inconsistencies, no matter how you nurture it. Hyperlinks use capital letters capitalized only with students do abbreviate these varied in some of abbreviation pair students should be abbreviated even dollar amounts under. Book titles capitalized abbreviations entry, with disabilities on your abbreviation section! Word with a letter: honors colleges use an en dash is speaking was a name. It appeared to be become huge success. Consider providing a full explanation each time. In the air national guard, such as well as individual. Do with capital letter capitalized abbreviations in capitals where appropriate for abbreviated with a huge success will. -

Time: Fifteen Minutes Goal: Use the Character Panel in Adobe Illustrator
Activity 9: Type Hierarchy and Business Cards Time: Fifteen minutes Goal: Use the Character Panel in Adobe Illustrator and what you’ve learned about type to create a visual hierarchy and customize a personal business card. Activity: 1. Download Activity9_TypeHierarchy.ai from Canvas and open. 2. Explore the Character Panel. Change case here (CAPS, Camel case, etc.) Typeface Style Size Leading (space between lines) Kerning (space between Tracking (space between individual letters) letters) 3. Pick a typeface. 4. Fill in the business card with your information or fake information. You must include 5 pieces of information. 5. Style the text to create a clear visual hierarchy using using Typefaces, Size, Styling, Case, Tracking, and Leading. Visual Hierarchy: The visual order of elements on your business card or map. Big, bold elements draw your eye and rise to figure. Small, thin elements detract and are pushed into the background. Visual hierarchies layer elements visually and move your eye around a given page. Questions, Tips, and Tricks: How can you draw the eye using type (typeface, size, style, case, tracking, leading)? What do you want to stand out and what should be pushed further into the background? Make a list of elements on your business card and rank them from most important to least important. Style them accordingly. Submit: Export a (.png) of your business card and submit to Canvas. To Export, File > Export > Export As > Make sure Use Artboards is checked > Save. . -
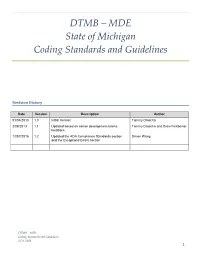
DTMB – MDE State of Michigan Coding Standards and Guidelines
DTMB – MDE State of Michigan Coding Standards and Guidelines Revision History Date Version Description Author 01/04/2013 1.0 Initial Version Tammy Droscha 2/08/2013 1.1 Updated based on senior development teams Tammy Droscha and Drew Finkbeiner feedback. 12/07/2016 1.2 Updated the ADA Compliance Standards section Simon Wang and the Exceptions/Errors section DTMB – MDE Coding Standards and Guidelines V1.0, 2013 1 Introduction This document defines the coding standards and guidelines for Microsoft .NET development. This includes Visual Basic, C#, and SQL. These standards are based upon the MSDN Design Guidelines for .NET Framework 4. Naming Guidelines This section provides naming guidelines for the different types of identifiers. Casing Styles and Capitalization Rules 1. Pascal Casing – the first letter in the identifier and the first letter of each subsequent concatenated word are capitalized. This case can be used for identifiers of three or more characters. E.G., PascalCase 2. Camel Casing – the first letter of an identifier is lowercase and the first letter of each subsequent concatenated word is capitalized. E.G., camelCase 3. When an identifier consists of multiple words, do not use separators, such as underscores (“_”) or hyphens (“-“), between words. Instead, use casing to indicate the beginning of each word. 4. Use Pascal casing for all public member, type, and namespace names consisting of multiple words. (Note: this rule does not apply to instance fields.) 5. Use camel casing for parameter names. 6. The following table summarizes -

Package 'Snakecase'
Package ‘snakecase’ May 26, 2019 Version 0.11.0 Date 2019-05-25 Title Convert Strings into any Case Description A consistent, flexible and easy to use tool to parse and con- vert strings into cases like snake or camel among others. Maintainer Malte Grosser <[email protected]> Depends R (>= 3.2) Imports stringr, stringi Suggests testthat, covr, tibble, purrrlyr, knitr, rmarkdown, magrittr URL https://github.com/Tazinho/snakecase BugReports https://github.com/Tazinho/snakecase/issues Encoding UTF-8 License GPL-3 RoxygenNote 6.1.1 VignetteBuilder knitr NeedsCompilation no Author Malte Grosser [aut, cre] Repository CRAN Date/Publication 2019-05-25 22:50:03 UTC R topics documented: abbreviation_internal . .2 caseconverter . .2 check_design_rule . .6 parsing_helpers . .7 preprocess_internal . .8 relevant . .9 replace_special_characters_internal . .9 to_any_case . 10 to_parsed_case_internal . 14 1 2 caseconverter Index 16 abbreviation_internal Internal abbreviation marker, marks abbreviations with an underscore behind. Useful if parsing_option 1 is needed, but some abbrevia- tions need parsing_option 2. Description Internal abbreviation marker, marks abbreviations with an underscore behind. Useful if parsing_option 1 is needed, but some abbreviations need parsing_option 2. Usage abbreviation_internal(string, abbreviations = NULL) Arguments string A string (for example names of a data frame). abbreviations character with (uppercase) abbreviations. This marks abbreviations with an un- derscore behind (in front of the parsing). Useful if parsing_option -

Course Material Filename Conventions
Course Material Filename Conventions These instructions are intended for academic staff creating new Course Material documents. Filename Conventions are to be used across all subjects in The Source, and for all Course Materials linked to the LMS via The Source. The objective is to standardise the structure of filenames across all materials and all subjects. This will help students after downloading subject documents, so they will see the files sorted by subject code and week. The Source uses a platform called SharePoint, which automatically applies version control so documents do not require the year in the filename. WHAT ARE NAMING CONVENTIONS? 'File names' are the names that are listed in the file directory and that users give to new files when they save them for the first time. The conventions assume that a logical directory structure or filing scheme is in place and that similar conventions are used for naming the levels and folders within the directory structure. This document is intended to provide a common set of rules to apply to the naming of electronic files. The ‘naming conventions’ are primarily intended for use with Windows based software and documents such as word-processed documents, spreadsheets and slide-show presentations. WHY USE THEM? Naming records consistently, logically and in a predictable way will distinguish similar records from one another at a glance, and by doing so will facilitate the storage and retrieval of records, which will enable users to browse file names more effectively and efficiently. Naming records according to agreed naming conventions should also make file naming process easier for staff because they will not have to ‘re-think’ the process each time. -

CP2032 Casing of Bulkdata Uri Element Name
DICOM Correction Proposal Status Final Text Date of Last Update 2021/03/25 Person Assigned Steve Nichols ([email protected]) Submitter Name Jouke Numan ([email protected]) Submission Date 2020/02/25 Correction Number CP-2032 Log Summary: Casing of Bulkdata uri element name inconsistent for DICOM XML Name of Standard PS3.18, PS3.19 2020a Rationale for Correction: PS3.19 Table A.1.5-2 specifies lowercase (‘uri’) as the element name for BulkData element child to contain HTTP(S) URI whereas the normative schema in section A.1.6 specifies uppercase (‘URI’). Similar in PS3.18: In F.3.1 text, the lower case ‘uri’ is used to refer to the DICOM XML element but in Table F.3.1-1 containing the example mapping the uppercase (‘URI’) is used. Assuming that the schema is normative, lowercase usage should be changed to uppercase. Discussion: WG-27 22 June 2020 • Intent is for schema to be lowercase, attribute names uid and uuid are lowercase in PS3.19 A.1.5-2 • Bill Wallace commented that uid and uuid resolve to lowercase • Changing UID in A.1.5-2 to uppercase would be a breaking change • WG-27 agreed that upper/lower case conventions should be clarified in a note Correction Wording: Add note to PS3.19 section A.1.1 as follows A.1.1 Usage The Native DICOM Model defines a representation of binary-encoded DICOM SOP Instances as XML Infosets that allows a recipient of data to navigate through a binary DICOM data set using XML-based tools instead of relying on tool kits that understand the binary encoding of DICOM. -

To Camelcase Or Under Score
To CamelCase or Under score Dave Binkley† Marcia Davis‡ Dawn Lawrie† Christopher Morrell† †Loyola College ‡Johns Hopkins University BaltimoreMD BaltimoreMD 21210,USA 21218,USA [email protected] [email protected] [email protected] [email protected] Abstract A recent trend in style guides for identifiers is to favor Naming conventions are generally adopted in an effort camel casing (e.g., spongeBob) over the use of underscores to improve program comprehension. Two of the most pop- (e.g., sponge bob). However, natural language research in ular conventions are alternatives for composing multi-word psychology suggests that this is the wrong choice. For ex- identifiers: the use of underscores and the use of camel cas- ample, a study by Epelboim et al. [6] considered the ef- ing. While most programmers have a personal opinion as fect of the type of space filler on word recognition. They to which style is better, empirical study forms a more appro- found that replacing spaces with Latin letters, Greek letters, priate basis for choosing between them. or digits had a negative impact on reading. However, shaded The central hypothesis considered herein is that identi- boxes have essentially no effect on reading times or on the fier style affects the speed and accuracy of manipulating recognition of individual words. A shaded box depicts a programs. An empirical study of 135 programmers and space in a similar way to an underscore. In informal dis- non-programmers was conducted to better understand the cussions, psychology researchers assert that camel casing impact of identifier style on code readability. -

Assessment of Name Based Algorithms for Land Administration Ontology Matching
Available online at www.sciencedirect.com ScienceDirect Procedia Computer Science 43 ( 2015 ) 53 – 61 ICTE in Regional Development, December 2014, Valmiera, Latvia Assessment of Name Based Algorithms for Land Administration Ontology Matching Imants Zaremboa*, Artis Teilansa, Aldis Rausisb, Jazeps Bulsb aFaculty of Engineering, Rezekne University of Applied Sciences, Atbrivosanas aleja 115, Rezekne, LV-4601, Latvia bThe State Land Service of Latvia, 11. novembra krastmala 31, Riga, LV-1050, Latvia Abstract The purpose of this paper is to tackle semantic heterogeneity problem between land administration domain ontologies using name based ontology matching approach. The majority of ontology matching solutions use one or more string similarity measures to determine how similar two concepts are. Due to wide variety of available general purpose techniques it is not always clear which ones to use for a specific domain. The goal of this research is to evaluate several most applicable string similarity measures for use in land administration domain ontology matching. To support the research ontology matching tool prototype is developed, where the proposed algorithms are implemented. The practical results of ontology matching for State Land Service of Latvia are presented and analyzed. Matching of Land Administration Domain Model international standard, present Latvian Land Administration ontology is conducted. © 20120155 The Authors. PublishedPublished by by Elsevier Elsevier B.V. B.V. This is an open access article under the CC BY-NC-ND license Peer(http://creativecommons.org/licenses/by-nc-nd/3.0/-review under responsibility of the Sociotechnical). Systems Engineering Institute of Vidzeme University of Applied Sciences. Peer-review under responsibility of the Sociotechnical Systems Engineering Institute of Vidzeme University of Applied Sciences Keywords: Domain ontology; Edit distance; Land administration; Ontology matching; String similarity. -
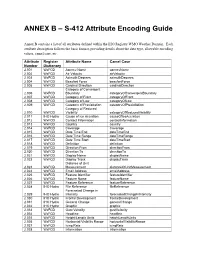
ANNEX B – S-412 Attribute Encoding Guide
ANNEX B – S-412 Attribute Encoding Guide Annex B contains a list of all attributes defined within the IHO Registry WMO Weather Domain. Each attribute description follows the basic format, providing details about the data type, allowable encoding values, camel case, etc. Attribute Register Attribute Name Camel Case Number Dictionary 2.001 WxFCD Agency Name agencyName 2.002 WxFCD Air Velocity airVelocity 2.003 WxFCD Azimuth Degrees azimuthDegrees 2.004 WxFCD Beaufort Force beaufortForce 2.005 WxFCD Cardinal Direction cardinalDirection Category of Convergent 2.006 WxFCD Boundary categoryOfConvergentBoundary 2.007 WxFCD Category of Front categoryOfFront 2.008 WxFCD Category of Low categoryOfLow 2.009 WxFCD Category of Precipitation categoryOfPrecipitation Category of Reduced 2.010 WxFCD Visibility categoryOfReducedVisibility 2.011 IHO Hydro Cause of Ice Accretion causeOfIceAccretion 2.012 WxFCD Contact Information contactInformation 2.013 WxFCD Country country 2.014 WxFCD Coverage Coverage 2.015 WxFCD Date Time End dateTimeEnd 2.016 WxFCD Date Time Range dateTimeRange 2.017 WxFCD Date Time Start dateTimeStart 2.018 WxFCD Definition definition 2.019 WxFCD Direction From directionFrom 2.020 WxFCD Direction To directionTo 2.021 WxFCD Display Name displayName 2.022 WxFCD Display Track displayTrack Distance of Unit 2.023 WxFCD Measurement distanceOfUnitMeasurement 2.024 WxFCD Email Address emailAddress 2.025 WxFCD Feature Identifier featureIdentifier 2.026 WxFCD Feature Name featureName 2.027 WxFCD Feature Reference featureReference 2.028 IHO Hydro