DOCSLIB.ORG

Relationships Between a Stock Market Price Index and Its Mutually Exclusive Subindices

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Relationships Between a Stock Market Price Index and Its Mutually Exclusive Subindices IUST International Journal of Engineering Science, Vol . 19 , No .5-2, 200 8, Page 27- 31 RELATIONSHIPS BETWEEN A STOCK MARKET PRICE INDEX AND ITS MUTUALLY EXCLUSIVE SUBINDICES Hamidreza Farhadi Abstract : In this article we find relationships between a stock market price index and its mutually exclusive subindices. In particular, we show th at when moving from one time to another, the return of such an index is a convex combination of the returns of its mutually exclusive subindices if at most one base adjustment is done. Keywords: stock market price index, mutually exclusive subindices, con vex combination 1. Introduction1 how optimistic or pessimistic people are about the This section is devoted to discuss some basics status of the economy in that period of time; therefore about the capital market indices, and to give the stock market indic es are used for economical motivation about the results to be discussed in the analyses too. section "Main Results" below. Those who want to get Generally a stock price index is in the form : to know more about the f ormulae and mechanisms of ca pital market price indices, could c onsult the M I = t Base Po int ( 1) references [1] and [ 3]. In this section one may also see t B the term "Free Float", a concept that found its way to t where the capital markets in the recent years; to learn about it , consult th e references [1], [2], and [ 3]. However , • "Base Point" can be any positive integer (usually the free float concept does not play a crucial role in taken to be 100 ). This value is fixed at all times. this paper . • M t is the (free-float adjusted, or total share) A stock market index compares the total market value market capital of the constituents of the index. of the companies in the index portfolio with the total This number is equal to the sum market value at a base point in time. Fo r example, if n the index value at the initial time was set to 100 and if M t = ∑ pit q it the current index value is 120 , this means that the i=1 average increase in prices has cause the market value where, pit is the price of stock i at time t , and to increase by 20% . q it is the number of shares of company i at time Stock market indices are constructed for various t. portfoli os of stocks. Some are constructed for large companies while some are constructed for small • Bt , called "base market value", is a number that companies. Indices are also constructed for different changes only when there is a change in the (free - industry sectors . Over 40 sector indices are now float adjusted, or total) number of shares of a calculated in Tehran StockArchive Exchange. ofsecurity SID in the index (see below); its value at the Capital market indice s have a few applications. As an initial time t = 0 is set equal to M.0 important of such applications , they are used as Since the "Base Point" is fixed throughout, we may benchmark for the performance of investment combine this value with the value B t (by substituting portfolios. The mutual funds who invest in the stock Bt markets, evaluate their performances against the Bt by ) to write the index in the form Base Po int performance of a benchmark s uch as S &P500 . As M another important application , the move ment of the t . This convention will not affect the results I t = stock market index in a period of time is a reflection of Bt given below as "Main Results", as the result s of tha t I Paper first received July . 15 , 200 7, and in revised form Dec . section are mainly built on the quotient t in which 19 , 2009. I Hamidreza Farhadi , Departm ent of Mathematical Sciences, Sharif t −1 University of Technology , the " Base Poi nt" cancels out. *Dedicated to FEAS (Federation of Euro -Asian Stock Exchanges) www.SID.ir 28 Relationships between a Stock Market Price Index and … 5enerally , two phenomena affect the total market "mutually exclusive subindices" of the index formed capital for a group of securities: one is the price on the set A of securities . So according to th is movement and the other is the change in the (fre e–float definition , "TOPIX Core 30 " and "TOPIX Large 70 " adjusted , or total) number of securities. Some of the are mutually exclusive subindices of "TOPIX 100 ". ways causing change in the number of shares are : 1) In this paper we are going to find relationships between adding a new security to the index , 2) deleting a a capital market index and its mut ually exclusive security from the index , 3) capital increase . A change subindices. Through oral communications with so me in M t caused by any of such events is not the result of people in the Tehran Stock Exchange back in July a fluctuation in the stock market. Therefore to remove 2005 , I noticed a wrong idea in them that if at some the effect of such change to M , a same proportional time the value of a main index falls between the values t of its mutually exclusive subindices, then from that change (increase or decrease, accordingly) needs to be time on, the value of the main index shoul d remain done to B.t For example, if a capital increase of is betwee n the values of those subindices. Providing an announced by a company at time −1t , the n the example below, we show that this idea is not generally increase in the value of the associated company causes true. T hen in proposition 1 of the section 2 we will the market cap M t−1 to increase to M t−1 ∆+ resulting prove the true relationship between a major index and its mutually exclusive subindice s. Subsequently, i n ∆ in a change of ×100 p ercent to M t−1 . Therefore proposition 2, we will give a generalization to the M t−1 counter example we are giving in the current section, the "base value" Bt−1 needs to increase accordingly to by showing that the values given in this example do not matter. ∆ For the sake of simplicity throughout this article, we Bt = 1+ × Bt−1 to secure the continuity of th e M t−1 assum e a m ajor index whose value at ti me t is denoted index when moving from time −1t to time t . The by I3,t , and its two mutually exclusive subindices value of ∆ could have been resulted by capital I and I. increase, deletion of a company from the index, 1,t 2,t addition of a company to the index, or some other ways. All such cases are treated similarly resulting in Example . Assume an index I3 together with its the identity mutually exclusive subi ndices I1 and I 2 whose values at time −1t are M+∆ M +∆ B=t−1 × B = t − 1 ( 2) tM t −1 I t−1 t − 1 I 1,t − 1 = 2000 I = 1000 M 2,t − 1 as I = t −1 . The value ∆ can be positive, t −1 I = 1000 • Bt −1 3,t − 1 negative, or zero (a value of zero corresponds to a phenomenon such as "stoc k split" where no adjustment So I3,t−1 is between I and I . Suppose that at to the base value is needed). 1,t − 1 2,t − 1 We explore more details on indices needed for the rest that time, th e market caps and the base value associated of this article, by looking at some example, e.g. the with these three indices are Tokyo Stock Exchange. The main stock price index at Tokyo Stock Exchange (TSE) is TOPIX . It is a (free– M1,t− 1=2000 , B 1, t − 1 = 1 float adjusted) value –weighted index. Various sub - M2,1t−=4000, B 2,1 t − = 4 indices of TOPIX are nowArchive calculated and published by of SID TSE. Depending on what sort of categorization is M3,1t−=6000 , B 3,1 t − = 6 • concerned, the companies forming a stock-market price index are grouped into non –overlapping subsets; then a Suppose that following time −1t and before the next price index is calculated on each group. For example, dissemination of the index at time t, a company in the the constituents of the "TOPIX 100" are those of the index I announces a capital increase of 10 unit of "TOPIX Core 30 " and "TOPIX Large 70 " combined. 1 As another example, the constituents of the TOPIX money. So the base value must be adjusted for time t. form three categories "Large -Si zed Stocks", "Medium - Since the same company is in the index I3 too, an Sized Stocks", and "Small -Sized Stocks" on each of adjustment is needed for both B1 and B3 (see E q. which an index is calculated. "TOPIX Sector Indices" (2)) : is another way of grouping the constituents of TOPIX. In general if a set A of companies is divided into M +10 2000+ 10 smaller groups A , A , … on each of which an B=1,t − 1 ×= B ×=1 1.005 1 2 1,tM 1, t − 1 2000 index is formed, then we call these partial indices 1,t − 1 www.SID.ir Hamidreza Farhadi 29 M ,t − 1 +10 6000+ 10 subindices. Suppose we have three indices I1 , I 2 and B3,t= ×= B 3,1 t − ×=6 6.01 • M 3,t − 1 6000 I3 with corresponding market caps M1 , M 2 and M 3 and the corresponding base values B1 , B2 and B3 .
Load more

Recommended publications
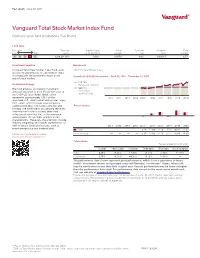
  • Vanguard Total Stock Market Index Fund
    Fact sheet | June 30, 2021 Vanguard® Vanguard Total Stock Market Index Fund Domestic stock fund | Institutional Plus Shares Fund facts Risk level Total net Expense ratio Ticker Turnover Inception Fund Low High assets as of 04/29/21 symbol rate date number 1 2 3 4 5 $269,281 MM 0.02% VSMPX 8.0% 04/28/15 1871 Investment objective Benchmark Vanguard Total Stock Market Index Fund seeks CRSP US Total Market Index to track the performance of a benchmark index that measures the investment return of the Growth of a $10,000 investment : April 30, 2015—D ecember 31, 2020 overall stock market. $20,143 Investment strategy Fund as of 12/31/20 The fund employs an indexing investment $20,131 approach designed to track the performance of Benchmark the CRSP US Total Market Index, which as of 12/31/20 represents approximately 100% of the 2011 2012 2013 2014 2015* 2016 2017 2018 2019 2020 investable U.S. stock market and includes large-, mid-, small-, and micro-cap stocks regularly traded on the New York Stock Exchange and Annual returns Nasdaq. The fund invests by sampling the index, meaning that it holds a broadly diversified collection of securities that, in the aggregate, approximates the full Index in terms of key characteristics. These key characteristics include industry weightings and market capitalization, as well as certain financial measures, such as Annual returns 2011 2012 2013 2014 2015* 2016 2017 2018 2019 2020 price/earnings ratio and dividend yield. Fund — — — — -3.28 12.69 21.19 -5.15 30.82 21.02 For the most up-to-date fund data, Benchmark — — — — -3.29 12.68 21.19 -5.17 30.84 20.99 please scan the QR code below.
    [Show full text]
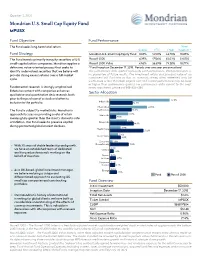
  • Current Fact Sheet
    Quarter 2, 2021 Mondrian U.S. Small Cap Equity Fund MPUSX Fund Objective Fund Performance The Fund seeks long-term total return. Since Quarter YTD 1 Year Inception * Fund Strategy Mondrian U.S. Small Cap Equity Fund 0.65%14.50% 44.76% 10.85% The Fund invests primarily in equity securities of U.S. Russell 2000 4.29%17.54% 62.03% 23.05% small-capitalization companies. Mondrian applies a Russell 2000 Value 4.56%26.69% 73.28% 18.77% defensive, value-oriented process that seeks to * Fund Inception December 17, 2018. Periods over one year are annualized identify undervalued securities that we believe will The performance data quoted represents past performance. Past performance is provide strong excess returns over a full market no guarantee of future results. The investment return and principal value of an cycle. investment will fluctuate so that an investor's shares, when redeemed, may be worth more or less than their original cost and current performance may be lower or higher than performance quoted. For performance data current to the most Fundamental research is strongly emphasized. recent month end, please call 888-832-4386. Extensive contact with companies enhances Sector Allocation qualitative and quantitative desk research, both prior to the purchase of a stock and after its 37.9% Industrials inclusion in the portfolio. 14.3% Information 23.6% The Fund is subject to market risks. Mondrian’s Technology 13.6% 11.8% approach focuses on providing a rate of return Materials meaningfully greater than the client’s domestic rate 3.8% 11.1% of inflation.
    [Show full text]
  • Bank of Japan's Exchange-Traded Fund Purchases As An
    ADBI Working Paper Series BANK OF JAPAN’S EXCHANGE-TRADED FUND PURCHASES AS AN UNPRECEDENTED MONETARY EASING POLICY Sayuri Shirai No. 865 August 2018 Asian Development Bank Institute Sayuri Shirai is a professor of Keio University and a visiting scholar at the Asian Development Bank Institute. The views expressed in this paper are the views of the author and do not necessarily reflect the views or policies of ADBI, ADB, its Board of Directors, or the governments they represent. ADBI does not guarantee the accuracy of the data included in this paper and accepts no responsibility for any consequences of their use. Terminology used may not necessarily be consistent with ADB official terms. Working papers are subject to formal revision and correction before they are finalized and considered published. The Working Paper series is a continuation of the formerly named Discussion Paper series; the numbering of the papers continued without interruption or change. ADBI’s working papers reflect initial ideas on a topic and are posted online for discussion. Some working papers may develop into other forms of publication. Suggested citation: Shirai, S.2018.Bank of Japan’s Exchange-Traded Fund Purchases as an Unprecedented Monetary Easing Policy.ADBI Working Paper 865. Tokyo: Asian Development Bank Institute. Available: https://www.adb.org/publications/boj-exchange-traded-fund-purchases- unprecedented-monetary-easing-policy Please contact the authors for information about this paper. Email: [email protected] Asian Development Bank Institute Kasumigaseki Building, 8th Floor 3-2-5 Kasumigaseki, Chiyoda-ku Tokyo 100-6008, Japan Tel: +81-3-3593-5500 Fax: +81-3-3593-5571 URL: www.adbi.org E-mail: [email protected] © 2018 Asian Development Bank Institute ADBI Working Paper 865 S.
    [Show full text]
  • Monthly Economic Update
    In this month’s recap: Stocks moved higher as investors looked past accelerating inflation and the Fed’s pivot on monetary policy. Monthly Economic Update Presented by Ray Lazcano, July 2021 U.S. Markets Stocks moved higher last month as investors looked past accelerating inflation and the Fed’s pivot on monetary policy. The Dow Jones Industrial Average slipped 0.07 percent, but the Standard & Poor’s 500 Index rose 2.22 percent. The Nasdaq Composite led, gaining 5.49 percent.1 Inflation Report The May Consumer Price Index came in above expectations. Prices increased by 5 percent for the year-over-year period—the fastest rate in nearly 13 years. Despite the surprise, markets rallied on the news, sending the S&P 500 to a new record close and the technology-heavy Nasdaq Composite higher.2 Fed Pivot The Fed indicated that two interest rate hikes in 2023 were likely, despite signals as recently as March 2021 that rates would remain unchanged until 2024. The Fed also raised its inflation expectations to 3.4 percent, up from its March projection of 2.4 percent. This news unsettled 3 the markets, but the shock was short-lived. News-Driven Rally In the final full week of trading, stocks rallied on the news of an agreement regarding the $1 trillion infrastructure bill and reports that banks had passed the latest Federal Reserve stress tests. Sector Scorecard 07072021-WR-3766 Industry sector performance was mixed. Gains were realized in Communication Services (+2.96 percent), Consumer Discretionary (+3.22 percent), Energy (+1.92 percent), Health Care (+1.97 percent), Real Estate (+3.28 percent), and Technology (+6.81 percent).
    [Show full text]
  • Vanguard Total Stock Market Index Fund
    Fact sheet | June 30, 2021 Vanguard® Vanguard Total Stock Market Index Fund Domestic stock fund | Institutional Shares Fund facts Risk level Total net Expense ratio Ticker Turnover Inception Fund Low High assets as of 04/29/21 symbol rate date number 1 2 3 4 5 $227,984 MM 0.03% VITSX 8.0% 07/07/97 0855 Investment objective Benchmark Vanguard Total Stock Market Index Fund seeks Spliced Total Stock Market Index to track the performance of a benchmark index that measures the investment return of the Growth of a $10,000 investment : January 31, 2011—D ecember 31, 2020 overall stock market. $35,603 Investment strategy Fund as of 12/31/20 The fund employs an indexing investment $35,628 approach designed to track the performance of Benchmark the CRSP US Total Market Index, which as of 12/31/20 represents approximately 100% of the 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 investable U.S. stock market and includes large-, mid-, small-, and micro-cap stocks regularly traded on the New York Stock Exchange and Annual returns Nasdaq. The fund invests by sampling the index, meaning that it holds a broadly diversified collection of securities that, in the aggregate, approximates the full Index in terms of key characteristics. These key characteristics include industry weightings and market capitalization, as well as certain financial measures, such as Annual returns 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 price/earnings ratio and dividend yield. Fund 1.09 16.42 33.49 12.56 0.42 12.67 21.17 -5.16 30.81 21.00 For the most up-to-date fund data, Benchmark 1.08 16.44 33.51 12.58 0.40 12.68 21.19 -5.17 30.84 20.99 please scan the QR code below.
    [Show full text]
  • Investing in the Marketplace
    Investing in the Marketplace Prudential Retirement When you hear people talk about “the market,” you might think Did you know... we agree on what that means. Truth is, there are many indexes that represent differing segments of the market. And these …there is even indexes don’t always move in tandem. Understanding some of an index that the key ones can help you diversify your investments to better represent the economy as a whole. purports to track The Dow Jones Industrial Average (The Dow) is one of the oldest, most investor anxiety? well-know indexes and is often used to represent the economy as a Dubbed “The Fear whole. Truth is, though, The Dow only includes 30 stocks of the world’s largest, most influential companies. Why is it called an “average?” Index,” the proper Originally, it was computed by adding up the per-share price of its stocks, and dividing by the number of companies. name of the Chicago The Standard & Poor’s 500 Index (made up of 500 of the most widely- Board Options traded U.S. stocks) is larger and more diverse than The Dow. Because it represents about 70% of the total value of the U.S. stock market, the Exchange’s index is S&P 500 is a better indication of how the U.S. marketplace is moving as a whole. the VIX Index, Sometimes referred to as the “total stock market index,” the Wilshire and measures the 5000 Index includes about 7,000 of the more than 10,000 publicly traded companies with headquarters in the U.S.
    [Show full text]
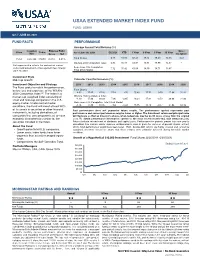
  • USAA Extended Market Index Fund Fact Sheet
    USAA EXTENDED MARKET INDEX FUND FUND: USMIX Q2 // JUNE 30, 2021 FUND FACTS PERFORMANCE Average Annual Total Returns (%) Inception Expense Ratio: Since Class Ticker As of June 30, 2021 Q2 2021 YTD 1 Year 3 Year 5 Year 10 Year Date Gross Net Inception Fund Shares 6.71 15.83 62.43 18.33 18.49 13.55 9.33 Fund 10/27/00 USMIX 0.42% 0.42% Wilshire 4500 Completion Index 6.83 16.11 63.07 18.81 18.99 14.32 – Net expense ratio reflects the contractual waiver Dow Jones U.S. Completion and/or reimbursement of management fees through 7.12 15.42 61.60 18.50 18.71 13.87 – June 30, 2023. Total Stock Market Investment Style Mid-Cap Growth Calendar Year Performance (%) Investment Objective and Strategy 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 The Fund seeks to match the performance, before fees and expenses, of the Wilshire Fund Shares -4.03 17.47 37.26 7.18 -3.76 15.48 17.72 -9.70 27.94 31.20 4500 Completion IndexSM. The Index is a market cap-weighted index consisting of Wilshire 4500 Completion Index -4.10 17.99 38.39 7.96 -2.65 17.84 -9.53 28.06 31.99 small and mid-cap companies in the U.S. 18.54 equity market. Under normal market Dow Jones U.S. Completion Total Stock Market conditions, the Fund will invest at least 80% -3.76 17.89 38.05 7.63 -3.42 15.75 18.12 -9.57 27.94 32.16 of its assets in securities or other financial Past performance does not guarantee future results.
    [Show full text]
  • September 2020
    From the desk of GS Wealth Management MONTHLY ECONOMIC UPDATE September 2020 MONTHLY QUOTE “You’ve got to get up every morning with THE MONTH IN BRIEF determination if you are going to go to bed with satisfaction.” U.S. Markets Stock prices surged in August as investors cheered positive news of a - George Lorimer potential COVID-19 treatment and welcomed a month-long succession of upbeat economic data. The Dow Jones Industrial Average rose 7.57 percent, the Standard & Poor’s 500 Index climbed 7.01 percent, and the Nasdaq Composite soared 9.59 MONTHLY TIP 1 percent. If you have a son or daughter graduating from college next Solid Foundation year, remind them to try and build an emergency fund. The month’s foundation was set by a series of strong economic reports, Those with the least including an increase in manufacturing activity, better-than-anticipated seniority can be the factory orders, and a lessening of new jobless claims.2,3,4 first to be laid off in the workplace, and sometimes that first Notching Highs job after college doesn’t work out. The S&P 500 index finally broke through resistance, ending the third week of August at a record high and completing the fastest bear market recovery in history. The Nasdaq Composite, having set multiple record highs during 5,6 the same week, also ended the month at a record high. Strong Close to the Month The final full week of trading was remarkable. Investors were encouraged by news of a potential COVID-19 treatment and a report suggesting U.S.
    [Show full text]
  • Description Index Attributes Methodology Construction Quick
    Equity S&P 500® Description The S&P 500® is widely regarded as the best single gauge of large-cap U.S. equities. There is over USD 7.8 trillion benchmarked to the index, with index assets comprising approximately USD 2.2 trillion of this total. The index includes 500 leading companies and captures approximately 80% coverage of available market capitalization. Index Attributes Created in 1957, the S&P 500 was the first U.S. market-cap-weighted stock market index. Today, it’s the basis of many listed and over-the-counter investment instruments. This world-renowned index includes 500 of the top companies in leading industries of the U.S. economy. The S&P 500 is part of a series of S&P Dow Jones U.S. equity indices that can be used as mutually exclusive building blocks; the index does not overlap holdings with the S&P MidCap 400® or S&P SmallCap 600®. Together, they constitute the S&P Composite 1500®. Methodology Construction • Universe. All constituents must be U.S. companies. • Eligibility Market Cap. Companies with market cap of USD 6.1 billion or greater. • Public Float. At least 50% of shares outstanding must be available for trading. • Financial Viability. Companies must have positive as-reported earnings over the most recent quarter, as well as over the most recent four quarters (summed together). • Adequate Liquidity and Reasonable Price. Consists of highly tradable common stocks, with active and deep markets. Quick Facts WEIGHTING METHOD Float-adjusted market cap weighted REBALANCING FREQUENCY "Quarterly in March, June, September, and December" CALCULATION FREQUENCY Real time CALCULATION CURRENCIES USD, AUD, BRL, CAD, CHF, EUR, GBP, HKD, JPY, MXN, SGD LAUNCH DATE March 4, 1957 For more information, including the complete methodology document, please visit: http://www.spindices.com/indices/equity/sp-500 All information for an index prior to its Launch Date is back-tested, based on the methodology that was in effect on the Launch Date.
    [Show full text]
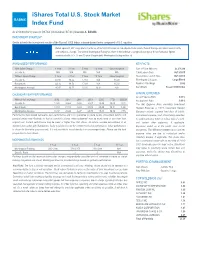
  • Ishares Total U.S. Stock Market Index Fund Fact Sheet
    iShares Total U.S. Stock Market BASMX Index Fund As of 06/30/2021 | Class K: BKTSX | Institutional: BITSX | Investor A: BASMX INVESTMENT STRATEGY Seeks to track the investment results of the Russell 3000 Index, a broad-based index composed of U.S. equities. Rated against 1,257 Large Blend Funds, as of 06/30/2021 based on risk adjusted total return. Overall Ratings are determined monthly and subject to change. The Overall Morningstar Rating for a fund is derived from a weighted average of the performance figures associated with its 3-, 5- and 10-year (if applicable) Morningstar Rating metrics.†† ANNUALIZED PERFORMANCE KEY FACTS With Sales Charge 1 Year 3 Year 5 Year 10 Year Since Inception Size of Fund (Millions) $2,278.2M Investor A N/A N/A N/A N/A N/A Fund Launch Date 08/13/2015 Without Sales Charge 1 Year 3 Year 5 Year 10 Year Since Inception Share Class Launch Date 08/13/2015 Investor A 43.90 18.42 17.51 N/A 15.00 Morningstar Category Large Blend Benchmark 44.16 18.73 17.89 N/A 15.30 Number of Holdings 2,892 Morningstar Average 40.47 16.77 16.15 13.21 N/A Benchmark Russell 3000 Index CALENDAR YEAR PERFORMANCE ANNUAL EXPENSES Gross Expense Ratio 0.31% Without Sales Charge 2016 2017 2018 2019 2020 YTD 2Q2021 Net Expense Ratio 0.31% Investor A 12.80 20.64 -5.55 30.69 20.49 15.00 8.20 The Net Expense Ratio excluding Investment Benchmark 12.74 21.13 -5.24 31.02 20.89 15.11 8.24 Related Expenses is 0.31% Investment Related Morningstar Average 10.37 20.44 -6.27 28.78 15.83 14.84 7.55 Expenses include acquired fund fees of 0.00%, Performance data quoted represents past performance and is no guarantee of future results.
    [Show full text]
  • Index US Fund P - ACC Shares for Investment Professionals Only FIDELITY INVESTMENT FUNDS MONTHLY PROFESSIONAL FACTSHEET INDEX US FUND P - ACC SHARES 31 AUGUST 2021
    pro.en.xx.20210831.GB00BJS8SH10.pdf Index US Fund P - ACC Shares For Investment Professionals Only FIDELITY INVESTMENT FUNDS MONTHLY PROFESSIONAL FACTSHEET INDEX US FUND P - ACC SHARES 31 AUGUST 2021 Strategy Fund Facts The fund is managed to track the performance of the S&P 500 index. ‘Index tracking’ is Launch date: 19.11.12 also known as passive investment management. While the fund is designed to replicate Fund size: £3,082m the characteristics of the index, it may not necessarily hold all the company shares that Number of positions in fund: 501 make up the index, or hold shares in exactly the same weightings as the index. The Fund reference currency: UK Sterling (GBP) costs that the fund incurs mean that its returns may not match the combined Fund domicile: United Kingdom performance of the shares included in the index. Fund legal structure: OEIC Management company: FIL Investment Services (UK) Limited The fund is managed by Geode Capital Management LLC, which is based in Boston Capital guarantee: No and is a leading specialist in the management of index-based strategies. They have Portfolio Turnover Cost (PTC): 0.00% managed equity index strategies with a team-based approach since 2002. Portfolio Turnover Rate (PTR): 16.52% Objectives & Investment Policy Share Class Facts • The fund aims to track the performance (before fees and expenses are applied) of the S&P 500 Other share classes may be available. Please refer to the prospectus for more details. (NUK) Index, thereby seeking to increase the value of your investment over 5 years or more.
    [Show full text]
  • Arxiv:2003.01859V1 [Q-Fin.ST] 29 Feb 2020
    Applications of deep learning in stock market prediction: recent progress Weiwei Jiang∗ Department of Electronic Engineering, Tsinghua University, Beijing 100084, China Abstract Stock market prediction has been a classical yet challenging problem, with the attention from both economists and computer scientists. With the purpose of building an effective prediction model, both linear and machine learning tools have been explored for the past couple of decades. Lately, deep learning models have been introduced as new frontiers for this topic and the rapid development is too fast to catch up. Hence, our motivation for this survey is to give a latest review of recent works on deep learning models for stock market prediction. We not only category the different data sources, various neural network structures, and common used evaluation metrics, but also the implementation and repro- ducibility. Our goal is to help the interested researchers to synchronize with the latest progress and also help them to easily reproduce the previous stud- ies as baselines. Base on the summary, we also highlight some future research directions in this topic. Keywords: Stock market prediction, deep learning, machine learning, feedforward neural network, convolutional neural network, recurrent neural network arXiv:2003.01859v1 [q-fin.ST] 29 Feb 2020 1. Introduction Stock market prediction is a classical problem in the intersection of finance and computer science. For this problem, the famous efficient market hypoth- ∗Corresponding author. E-mail address: [email protected] Preprint submitted to Elsevier Journal March 5, 2020 esis (EMH) gives a pessimistic view and implies that financial market is ef- ficient (Fama, 1965), which maintains that technical analysis or fundamental analysis (or any analysis) would not yield any consistent over-average profit to investors.
    [Show full text]