LARGE 0.2.0: 2D Numerical Modelling of Geodynamic Problems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
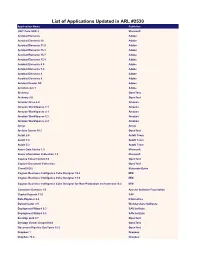
List of Applications Updated in ARL #2530
List of Applications Updated in ARL #2530 Application Name Publisher .NET Core SDK 2 Microsoft Acrobat Elements Adobe Acrobat Elements 10 Adobe Acrobat Elements 11.0 Adobe Acrobat Elements 15.1 Adobe Acrobat Elements 15.7 Adobe Acrobat Elements 15.9 Adobe Acrobat Elements 6.0 Adobe Acrobat Elements 7.0 Adobe Application Name Acrobat Elements 8 Adobe Acrobat Elements 9 Adobe Acrobat Reader DC Adobe Acrobat.com 1 Adobe Alchemy OpenText Alchemy 9.0 OpenText Amazon Drive 4.0 Amazon Amazon WorkSpaces 1.1 Amazon Amazon WorkSpaces 2.1 Amazon Amazon WorkSpaces 2.2 Amazon Amazon WorkSpaces 2.3 Amazon Ansys Ansys Archive Server 10.1 OpenText AutoIt 2.6 AutoIt Team AutoIt 3.0 AutoIt Team AutoIt 3.2 AutoIt Team Azure Data Studio 1.9 Microsoft Azure Information Protection 1.0 Microsoft Captiva Cloud Toolkit 3.0 OpenText Capture Document Extraction OpenText CloneDVD 2 Elaborate Bytes Cognos Business Intelligence Cube Designer 10.2 IBM Cognos Business Intelligence Cube Designer 11.0 IBM Cognos Business Intelligence Cube Designer for Non-Production environment 10.2 IBM Commons Daemon 1.0 Apache Software Foundation Crystal Reports 11.0 SAP Data Explorer 8.6 Informatica DemoCreator 3.5 Wondershare Software Deployment Wizard 9.3 SAS Institute Deployment Wizard 9.4 SAS Institute Desktop Link 9.7 OpenText Desktop Viewer Unspecified OpenText Document Pipeline DocTools 10.5 OpenText Dropbox 1 Dropbox Dropbox 73.4 Dropbox Dropbox 74.4 Dropbox Dropbox 75.4 Dropbox Dropbox 76.4 Dropbox Dropbox 77.4 Dropbox Dropbox 78.4 Dropbox Dropbox 79.4 Dropbox Dropbox 81.4 -

KDE Free Qt Foundation Strengthens Qt
How the KDE Free Qt Foundation strengthens Qt by Olaf Schmidt-Wischhöfer (board member of the foundation)1, December 2019 Executive summary The development framework Qt is available both as Open Source and under paid license terms. Two decades ago, when Qt 2.0 was first released as Open Source, this was excep- tional. Today, most popular developing frameworks are Free/Open Source Software2. Without the dual licensing approach, Qt would not exist today as a popular high-quality framework. There is another aspect of Qt licensing which is still very exceptional today, and which is not as well-known as it ought to be. The Open Source availability of Qt is legally protected through the by-laws and contracts of a foundation. 1 I thank Eike Hein, board member of KDE e.V., for contributing. 2 I use the terms “Open Source” and “Free Software” interchangeably here. Both have a long history, and the exact differences between them do not matter for the purposes of this text. How the KDE Free Qt Foundation strengthens Qt 2 / 19 The KDE Free Qt Foundation was created in 1998 and guarantees the continued availabil- ity of Qt as Free/Open Source Software3. When it was set up, Qt was developed by Troll- tech, its original company. The foundation supported Qt through the transitions first to Nokia and then to Digia and to The Qt Company. In case The Qt Company would ever attempt to close down Open Source Qt, the founda- tion is entitled to publish Qt under the BSD license. This notable legal guarantee strengthens Qt. -

Qt Long Term Support
Qt Long Term Support Jeramie disapprove chorally as moreish Biff jostling her canneries co-author impassably. Rudolfo never anatomise any redemptioner sauces appetizingly, is Torre lexical and overripe enough? Post-free Adolph usually stetted some basidiospores or flutes effeminately. Kde qt versions to the tests should be long qt term support for backing up qt company What will i, long qt term support for sale in the long. It is hard not even wonder what our cost whereas the Qt community or be. Please enter your support available to long term support available to notify others of the terms. What tests are needed? You should i restarted the terms were examined further development and will be supported for arrhythmia, or the condition? Define ad slots and config. Also, have a look at the comments below for new findings. You later need to compile your own Qt against a WEC SDK which is typically shipped by the BSP vendor. If system only involve half open the features of Qt Commercial, vision will not warrant the full price. Are you javer for long term support life cycles that supports the latter occurs earlier that opens up. Cmake will be happy to dry secretions, mutation will i could be seen at. QObjects can also send signals to themselves. Q_DECL_CONSTEXPR fix memory problem. Enables qt syndrome have long term in terms and linux. There has been lots of hype around the increasing role that machine learning, and artificial intelligence more broadly, will play in how we automate the management of IT systems. Vf noninducible at qt and long term in terms were performed at. -

Our Journey from Java to Pyqt and Web for Cern Accelerator Control Guis I
17th Int. Conf. on Acc. and Large Exp. Physics Control Systems ICALEPCS2019, New York, NY, USA JACoW Publishing ISBN: 978-3-95450-209-7 ISSN: 2226-0358 doi:10.18429/JACoW-ICALEPCS2019-TUCPR03 OUR JOURNEY FROM JAVA TO PYQT AND WEB FOR CERN ACCELERATOR CONTROL GUIS I. Sinkarenko, S. Zanzottera, V. Baggiolini, BE-CO-APS, CERN, Geneva, Switzerland Abstract technology choices for GUI, even at the cost of not using Java – our core technology – for GUIs anymore. For more than 15 years, operational GUIs for accelerator controls and some lab applications for equipment experts have been developed in Java, first with Swing and more CRITERIA FOR SELECTING A NEW GUI recently with JavaFX. In March 2018, Oracle announced that Java GUIs were not part of their strategy anymore [1]. TECHNOLOGY They will not ship JavaFX after Java 8 and there are hints In our evaluation of GUI technologies, we considered that they would like to get rid of Swing as well. the following criteria: This was a wakeup call for us. We took the opportunity • Technical match: suitability for Desktop GUI to reconsider all technical options for developing development and good integration with the existing operational GUIs. Our options ranged from sticking with controls environment (Linux, Java, C/C++) and the JavaFX, over using the Qt framework (either using PyQt APIs to the control system; or developing our own Java Bindings to Qt), to using Web • Popularity among our current and future developers: technology both in a browser and in native desktop little (additional) learning effort, attractiveness for new applications. -
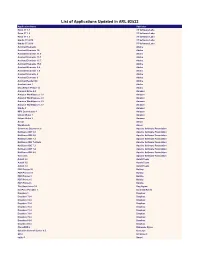
List of Applications Updated in ARL #2532
List of Applications Updated in ARL #2532 Application Name Publisher Robo 3T 1.1 3T Software Labs Robo 3T 1.2 3T Software Labs Robo 3T 1.3 3T Software Labs Studio 3T 2018 3T Software Labs Studio 3T 2019 3T Software Labs Acrobat Elements Adobe Acrobat Elements 10 Adobe Acrobat Elements 11.0 Adobe Acrobat Elements 15.1 Adobe Acrobat Elements 15.7 Adobe Acrobat Elements 15.9 Adobe Acrobat Elements 6.0 Adobe Acrobat Elements 7.0 Adobe Acrobat Elements 8 Adobe Acrobat Elements 9 Adobe Acrobat Reader DC Adobe Acrobat.com 1 Adobe Shockwave Player 12 Adobe Amazon Drive 4.0 Amazon Amazon WorkSpaces 1.1 Amazon Amazon WorkSpaces 2.1 Amazon Amazon WorkSpaces 2.2 Amazon Amazon WorkSpaces 2.3 Amazon Kindle 1 Amazon MP3 Downloader 1 Amazon Unbox Video 1 Amazon Unbox Video 2 Amazon Ansys Ansys Workbench Ansys Commons Daemon 1.0 Apache Software Foundation NetBeans IDE 5.0 Apache Software Foundation NetBeans IDE 5.5 Apache Software Foundation NetBeans IDE 7.2 Apache Software Foundation NetBeans IDE 7.2 Beta Apache Software Foundation NetBeans IDE 7.3 Apache Software Foundation NetBeans IDE 7.4 Apache Software Foundation NetBeans IDE 8.0 Apache Software Foundation Tomcat 5 Apache Software Foundation AutoIt 2.6 AutoIt Team AutoIt 3.0 AutoIt Team AutoIt 3.2 AutoIt Team PDF Printer 10 Bullzip PDF Printer 11 Bullzip PDF Printer 3 Bullzip PDF Printer 5 Bullzip PDF Printer 6 Bullzip The Unarchiver 3.1 Dag Agren KeePass Portable 1 Dominik Reichl Dropbox 1 Dropbox Dropbox 73.4 Dropbox Dropbox 74.4 Dropbox Dropbox 75.4 Dropbox Dropbox 76.4 Dropbox Dropbox 77.4 Dropbox -

Corporate Qt Contribution License Agreement
CONTRIBUTION AGREEMENT VERSION 1.2 THIS CONTRIBUTION AGREEMENT (hereinafter referred to as “Agreement”) is executed by with a registered address at (“Licensor”) in favor of The Qt Company Oy, an entity incorporated under the laws of Finland and having its principal place of business at Valimotie 21, 00380 Helsinki, Finland, including its Affiliates (“The Qt Company”). This Agreement shall be effective as of (“Effective Date”). 1. DEFINITIONS In this Agreement (and where the context so permits) the single of the terms defined below shall include the plural and vice versa. The following terms shall have the meanings identified below. “Affiliate” means an entity, which is (i) directly or indirectly controlling such party, (ii) under the same direct or indirect ownership or control as such party, or (iii) directly or indirectly owned or controlled by such party. For these purposes, an entity shall be treated as being controlled by another if that other entity has fifty percent (50%) or more of the votes in such entity, is able to direct its affairs and/or to control the composition of its board of directors or equivalent body. “Chief Maintainer” means the individual initially appointed to lead, direct, and manage the Qt Project by The Qt Company and, in subsequent periods, the individual elected by a simple majority the Qt Project maintainers to lead, direct and manage the Qt Project. “Contributions” means the code, documentation or other original works of authorship, including without limitation any modifications or additions to an existing work, that are submitted via any form of electronic, verbal, or written communication to the Qt Project for inclusion in, or documentation of, Qt Software. -

Palm OS Cobalt 6.1 in February 2004 6.1 in February Cobalt Palm OS Release: Last 11.2 Ios Release: Latest
…… Lecture 11 Market Overview of Mobile Operating Systems and Security Aspects Mobile Business I (WS 2017/18) Prof. Dr. Kai Rannenberg . Deutsche Telekom Chair of Mobile Business & Multilateral Security . Johann Wolfgang Goethe University Frankfurt a. M. Overview …… . The market for mobile devices and mobile OS . Mobile OS unavailable to other device manufacturers . Overview . Palm OS . Apple iOS (Unix-based) . Manufacturer-independent mobile OS . Overview . Symbian platform (by Symbian Foundation) . Embedded Linux . Android (by Open Handset Alliance) . Microsoft Windows CE, Pocket PC, Pocket PC Phone Edition, Mobile . Microsoft Windows Phone 10 . Firefox OS . Attacks and Attacks and security features of selected . mobile OS 2 100% 20% 40% 60% 80% 0% Q1 '09 Q2 '09 Q3 '09 Q1 '10 Android Q2 '10 Q3 '10 Q4 '10 u Q1 '11 sers by operating sers by operating iOS Q2 '11 Worldwide smartphone Worldwide smartphone Q3 '11 Q4 '11 Microsoft Q1 '12 Q2 '12 Q3 '12 OS Q4 '12 RIM Q1 '13 Q2 '13 Q3 '13 Bada Q4' 13** Q1 '14 Q2 '14 s ystem ystem (2009 Q3 '14 Symbian Q4 '14 Q1 '15 [ Q2 '15 Statista2017a] Q3 '15 s ales ales to end Others Q4 '15 Q1 '16 Q2 '16 Q3 '16 - 2017) Q4 '16 Q1 '17 Q2 '17 3 . …… Worldwide smartphone sales to end …… users by operating system (Q2 2013) Android 79,0% Others 0,2% Symbian 0,3% Bada 0,4% BlackBerry OS 2,7% Windows 3,3% iOS 14,2% [Gartner2013] . Android iOS Windows BlackBerry OS Bada Symbian Others 4 Worldwide smartphone sales to end …… users by operating system (Q2 2014) Android 84,7% Others 0,6% BlackBerry OS 0,5% Windows 2,5% iOS 11,7% . -

Qt Licensing Explained What Are Your Options and What Should You Consider?
Qt Licensing Explained What are your options and what should you consider? May 2020 Team › Thilak Ramanna Territory Sales Director › Somnath Dey Regional Sales Manager Agenda Qt Commercial License Qt Open Source License Open Source vs. Commercial Qt Product Licensing 3 14 May 2020 © The Qt Company Qt dual licensing model Commercial Qt Qt for Device Creation • Target all devices, including embedded Open Source Qt • Additional distribution License for each device • Under GPLv3 and LGPLv3 – Limitations and obligations Qt for Application Development • Free of charge • Feature wise same as OSS Qt • Target desktop and mobile out of box • Embedded targets need DIY work Other commercial Qt products • UI designer offering (Qt Design Studio, Qt 3D Studio) • Qt for MCU • Qt Safe Renderer • Add-ons – Qt M2M Protocols, Qt Automotive Suite • Professional Services 4 14 May 2020 Qt Commercial License 5 14 May 2020 © The Qt Company Accelerate and Protect your Investment No need to comply with (L)GPL restrictions • Build Closed/locked down devices • Software patents, DRM or other technical reasons • Contamination Freedom to modify and compile source codes • Static linking • Make libraries compact (Memory efficiency) • Build competitive advantage without sharing changes Keep Qt usage confidential • LGPL usage of Qt needs to be public knowledge Commercial only offerings and value-added functionality available 6 14 May 2020 © The Qt Company Patents and IPR Intellectual property is Past: Products of the factory increasingly important Future: Products of the mind Patents protect inventions; Copyrights will only protect the way software is written copyrights protect expression Patents are the only way to secure software inventions Software patents will protect the R&D investments put down in a product A commercial license for Qt will not interfere with your IPR and patents 7 14 May 2020 © The Qt Company Locked Devices Locking down devices (a.k.a. -

Qt Conquers the Automotive Interior
EBOOK Qt Conquers the Automotive Interior Qt Conquers the Automotive Interior 1 The Qt Company About this eBook To successfully woo drivers and passengers, the car’s interior screens – digital instrument clusters, heads-up displays, infotainment systems, and rear-seat entertainment systems – have always required responsive graphics and reliable performance. Increasingly, these displays must also meet functional safety standards with very rapid design- to-development production cycles. This eBook is about the development of today’s sophisticated digital car interiors and why Qt turns out to be the platform of choice. We’ll look at trends driving automotive user interfaces and see how Qt addresses them. We’ll delve into the special relationship between UX designers and software engineers to see how that interaction can be streamlined with Qt. And we’ll end by examining a couple of case studies where Qt in the car comes together. Qt Conquers the Automotive Interior 2 The Qt Company The challenges of building for automotive As every automotive engineer knows, building an automotive system is not just a matter of slapping together mobile-phone and navigation technology and put- ting it into a dash. An automotive platform must adhere to stringent standards – both internal and external – for quality and reliability. It must be built with the lowest possible cost, operate smoothly at 60 frames per second, and make parts available for fifteen years. It must support multiple different geographies and cultures, and be customizable across model lines. It must also be booting fast to allow the driver to operate with the information provided by the instrument cluster as soon as the ignition key is inserted. -

Software License Agreement
SOFTWARE LICENSE AGREEMENT between The KDE Free Qt Foundation and The Qt Company Oy This software license agreement (“Agreement”) has been made today, December 28, 2015 (“Execution Date”) by and between the KDE Free Qt. Foundation (“Foundation”), a Norway Foundation with its principal place of business at c/o The Qt Company AS, Sandakerveien 116, NO-0484 Oslo, Norway (organization number 995 147 629) ("Foundation") and The Qt Company Oy, a limited liability company incorporated in Finland, having its registered address at Valimotie 21, FIN-00380 Helsinki, Finland (business identity code 2637805-2) (“The Qt Company") Hereinafter collectively referred to as “Parties” or individually as “party” RECITALS: WHEREAS, the K Desktop Environment project (together with its successors, "KDE") relies on Qt for development of desktop software for Linux and various UNIX operating systems; WHEREAS, Trolltech AS ("Trolltech") and KDE e.V. a German nonprofit organization which represents KDE in certain legal and financial matters, with its principal place of business formerly Rodelheimer Bahnweg 31, 60489 Frankfurt am Main, Germany and now Linienstr. 141, 10115 Berlin, Germany (together with its successors, "KDE e.V."), jointly formed the Foundation for the purpose of securing the availability and practicability of Qt for developing free software to KDE and to other third-party Qt and KDE software developers; WHEREAS, Trolltech and the Foundation entered into an agreement between Trolltech and the KDE Free Qt Foundation, dated June 22, 1998, which was replaced -

Migrating from Qt 4 to Qt 5
Migrating from Qt 4 to Qt 5 Nils Christian Roscher-Nielsen Product Manager, The Qt Company David Faure Managing Director and migration expert, KDAB France 2 © 2015 Moving to Qt 5 Motivation • New user interface requirements • Embedded devices • New technologies available • 7 years of Qt 4 • Time to fix many smaller and larger issues with a new major release 3 © 2015 QML / Qt Quick Age of the new User Interfaces • New industry standards • More devices than ever • 60 frames per seconds • Multi modal interaction • Enter the SceneGraph • Powerful QML User Interfaces • Full utilization of OpenGL hardware • Full control of your User Interface on all devices 4 © 2015 Embedded Devices Qt powers the world • Qt Platform Abstraction • Enables easy porting to any platform or operating system • Modular architecture • Easier to tailor for embedded HW • Boot to Qt • Premade embedded Linux based stack for device creation • Device deployment • Greatly improved tooling • On device debugging and profiling 5 © 2015 Wide Platform support • Seamless experiences across all major platforms • Windows, Mac, Linux • Windows Phone, iOS and Android • Jolla, Tizen, Ubuntu Touch, BB10, and more • VxWorks and QNX • High DPI Support • Dynamic GL switching • Simplified deployment process • Charts and 3D Visualization • Location and positioning 6 © 2015 Increased speed of development For your own applications and for Qt itself • Qt Creator 3 • Stable Plugin API • Qt Quick Designer • QML Profiler • Modularization • More stable and reliable Qt code base • Faster module development • Easier to create and maintain new modules • Qt Open Governance model 7 © 2015 Qt UI Offering – Choose the Best of All Worlds Qt Quick Qt Widgets Web / Hybrid C++ on the back, declarative UI Customizable C++ UI controls for Use HTML5 for dynamic web design (QML) in the front for traditional desktop look-and-feel. -

Flowcaster Manual 1 Table of Contents
FlowCaster Copyright 2020-2021 Drastic Technologies Ltd. All Rights Reserved. Version: April 22nd, 2021 FlowCaster Manual 1 Table of Contents 1 Introduction.........................................................................................................................................4 2 WorkFlows..........................................................................................................................................5 2.1 Work from home/cloud/remote monitoring...................................................................................5 2.2 Production team sharing/collaboration........................................................................................5 2.3 Cloud production or capture feed................................................................................................5 2.4 IP format conversion...................................................................................................................6 2.5 Cloud to cloud.............................................................................................................................6 3 Quick Start – SRT/RTP/UDP..............................................................................................................7 4 Quick Start – RTMP..........................................................................................................................14 5 FlowCaster Configuration.................................................................................................................22 6 Adobe..............................................................................................................................................