Appendix a Transforms and Sampling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bring Down the Two-Language Barrier with Julia Language for Efficient
AbstractSDRs: Bring down the two-language barrier with Julia Language for efficient SDR prototyping Corentin Lavaud, Robin Gerzaguet, Matthieu Gautier, Olivier Berder To cite this version: Corentin Lavaud, Robin Gerzaguet, Matthieu Gautier, Olivier Berder. AbstractSDRs: Bring down the two-language barrier with Julia Language for efficient SDR prototyping. IEEE Embedded Systems Letters, Institute of Electrical and Electronics Engineers, 2021, pp.1-1. 10.1109/LES.2021.3054174. hal-03122623 HAL Id: hal-03122623 https://hal.archives-ouvertes.fr/hal-03122623 Submitted on 27 Jan 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. AbstractSDRs: Bring down the two-language barrier with Julia Language for efficient SDR prototyping Corentin LAVAUD∗, Robin GERZAGUET∗, Matthieu GAUTIER∗, Olivier BERDER∗. ∗ Univ Rennes, CNRS, IRISA, [email protected] Abstract—This paper proposes a new methodology based glue interface [8]. Regarding programming semantic, low- on the recently proposed Julia language for efficient Software level languages (e.g. C++/C, Rust) offers very good runtime Defined Radio (SDR) prototyping. SDRs are immensely popular performance but does not offer a good prototyping experience. as they allow to have a flexible approach for sounding, monitoring or processing radio signals through the use of generic analog High-level languages (e.g. -

SEISGAMA: a Free C# Based Seismic Data Processing Software Platform
Hindawi International Journal of Geophysics Volume 2018, Article ID 2913591, 8 pages https://doi.org/10.1155/2018/2913591 Research Article SEISGAMA: A Free C# Based Seismic Data Processing Software Platform Theodosius Marwan Irnaka, Wahyudi Wahyudi, Eddy Hartantyo, Adien Akhmad Mufaqih, Ade Anggraini, and Wiwit Suryanto Seismology Research Group, Physics Department, Faculty of Mathematics and Natural Sciences, Universitas Gadjah Mada, Sekip Utara Bulaksumur, Yogyakarta 55281, Indonesia Correspondence should be addressed to Wiwit Suryanto; [email protected] Received 4 July 2017; Accepted 24 December 2017; Published 30 January 2018 Academic Editor: Filippos Vallianatos Copyright © 2018 Teodosius Marwan Irnaka et al. Tis is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Seismic refection is one of the most popular methods in geophysical prospecting. Nevertheless, obtaining high resolution and accurate results requires a sophisticated processing stage. Tere are many open-source seismic refection data processing sofware programs available; however, they ofen use a high-level programming language that decreases its overall performance, lacks intuitive user-interfaces, and is limited to a small set of tasks. Tese shortcomings reveal the need to develop new sofware using a programming language that is natively supported by Windows5 operating systems, which uses a relatively medium-level programming language (such as C#) and can be enhanced by an intuitive user interface. SEISGAMA was designed to address this need and employs a modular concept, where each processing group is combined into one module to ensure continuous and easy development and documentation. -

Julia: a Modern Language for Modern ML
Julia: A modern language for modern ML Dr. Viral Shah and Dr. Simon Byrne www.juliacomputing.com What we do: Modernize Technical Computing Today’s technical computing landscape: • Develop new learning algorithms • Run them in parallel on large datasets • Leverage accelerators like GPUs, Xeon Phis • Embed into intelligent products “Business as usual” will simply not do! General Micro-benchmarks: Julia performs almost as fast as C • 10X faster than Python • 100X faster than R & MATLAB Performance benchmark relative to C. A value of 1 means as fast as C. Lower values are better. A real application: Gillespie simulations in systems biology 745x faster than R • Gillespie simulations are used in the field of drug discovery. • Also used for simulations of epidemiological models to study disease propagation • Julia package (Gillespie.jl) is the state of the art in Gillespie simulations • https://github.com/openjournals/joss- papers/blob/master/joss.00042/10.21105.joss.00042.pdf Implementation Time per simulation (ms) R (GillespieSSA) 894.25 R (handcoded) 1087.94 Rcpp (handcoded) 1.31 Julia (Gillespie.jl) 3.99 Julia (Gillespie.jl, passing object) 1.78 Julia (handcoded) 1.2 Those who convert ideas to products fastest will win Computer Quants develop Scientists prepare algorithms The last 25 years for production (Python, R, SAS, DEPLOY (C++, C#, Java) Matlab) Quants and Computer Compress the Scientists DEPLOY innovation cycle collaborate on one platform - JULIA with Julia Julia offers competitive advantages to its users Julia is poised to become one of the Thank you for Julia. Yo u ' v e k i n d l ed leading tools deployed by developers serious excitement. -

The Modeling and Quantification of Rhythmic to Non-Rhythmic
Graduate Institute of Biomedical Electronics and Bioinformatics College of Electrical Engineering and Computer Science National Taiwan University Doctoral Dissertation The Modeling and Quantification of Rhythmic to Non-rhythmic Phenomenon in Electrocardiography during Anesthesia Author : Yu-Ting Lin Advisor : Jenho Tsao, Ph.D. arXiv:1502.02764v1 [q-bio.NC] 10 Feb 2015 February 2015 \All composite things are not constant. Work hard to gain your own enlightenment." Siddh¯arthaGautama Abstract Variations of instantaneous heart rate appears regularly oscillatory in deeper levels of anesthesia and less regular in lighter levels of anesthesia. It is impossible to observe this \rhythmic-to-non-rhythmic" phenomenon from raw electrocardiography waveform in cur- rent standard anesthesia monitors. To explore the possible clinical value, I proposed the adaptive harmonic model, which fits the descriptive property in physiology, and provides adequate mathematical conditions for the quantification. Based on the adaptive har- monic model, multitaper Synchrosqueezing transform was used to provide time-varying power spectrum, which facilitates to compute the quantitative index: \Non-rhythmic- to-Rhythmic Ratio" index (NRR index). I then used a clinical database to analyze the behavior of NRR index and compare it with other standard indices of anesthetic depth. The positive statistical results suggest that NRR index provides addition clinical infor- mation regarding motor reaction, which aligns with current standard tools. Furthermore, the ability to indicates the noxious stimulation is an additional finding. Lastly, I have proposed an real-time interpolation scheme to contribute my study further as a clinical application. Keywords: instantaneous heart rate; rhythmic-to-non-rhythmic; Synchrosqueezing trans- form; time-frequency analysis; time-varying power spectrum; depth of anesthesia; electro- cardiography Acknowledgements First of all, I would like to thank Professor Jenho Tsao for all thoughtful lessons, discus- sions, and guidance he has provided me in the last five years. -

Time-Frequency Analysis of Time-Varying Signals and Non-Stationary Processes
Time-Frequency Analysis of Time-Varying Signals and Non-Stationary Processes An Introduction Maria Sandsten 2020 CENTRUM SCIENTIARUM MATHEMATICARUM Centre for Mathematical Sciences Contents 1 Introduction 3 1.1 Spectral analysis history . 3 1.2 A time-frequency motivation example . 5 2 The spectrogram 9 2.1 Spectrum analysis . 9 2.2 The uncertainty principle . 10 2.3 STFT and spectrogram . 12 2.4 Gabor expansion . 14 2.5 Wavelet transform and scalogram . 17 2.6 Other transforms . 19 3 The Wigner distribution 21 3.1 Wigner distribution and Wigner spectrum . 21 3.2 Properties of the Wigner distribution . 23 3.3 Some special signals. 24 3.4 Time-frequency concentration . 25 3.5 Cross-terms . 27 3.6 Discrete Wigner distribution . 29 4 The ambiguity function and other representations 35 4.1 The four time-frequency domains . 35 4.2 Ambiguity function . 39 4.3 Doppler-frequency distribution . 44 5 Ambiguity kernels and the quadratic class 45 5.1 Ambiguity kernel . 45 5.2 Properties of the ambiguity kernel . 46 5.3 The Choi-Williams distribution . 48 5.4 Separable kernels . 52 1 Maria Sandsten CONTENTS 5.5 The Rihaczek distribution . 54 5.6 Kernel interpretation of the spectrogram . 57 5.7 Multitaper time-frequency analysis . 58 6 Optimal resolution of time-frequency spectra 61 6.1 Concentration measures . 61 6.2 Instantaneous frequency . 63 6.3 The reassignment technique . 65 6.4 Scaled reassigned spectrogram . 69 6.5 Other modern techniques for optimal resolution . 72 7 Stochastic time-frequency analysis 75 7.1 Definitions of non-stationary processes . -

On the Use of Time–Frequency Reassignment in Additive Sound Modeling*
PAPERS On the Use of Time–Frequency Reassignment in Additive Sound Modeling* KELLY FITZ, AES Member AND LIPPOLD HAKEN, AES Member Department of Electrical Engineering and Computer Science, Washington University, Pulman, WA 99164 A method of reassignment in sound modeling to produce a sharper, more robust additive representation is introduced. The reassigned bandwidth-enhanced additive model follows ridges in a time–frequency analysis to construct partials having both sinusoidal and noise characteristics. This model yields greater resolution in time and frequency than is possible using conventional additive techniques, and better preserves the temporal envelope of transient signals, even in modified reconstruction, without introducing new component types or cumbersome phase interpolation algorithms. 0INTRODUCTION manipulations [11], [12]. Peeters and Rodet [3] have developed a hybrid analysis/synthesis system that eschews The method of reassignment has been used to sharpen high-level transient models and retains unabridged OLA spectrograms in order to make them more readable [1], [2], (overlap–add) frame data at transient positions. This to measure sinusoidality, and to ensure optimal window hybrid representation represents unmodified transients per- alignment in the analysis of musical signals [3]. We use fectly, but also sacrifices homogeneity. Quatieri et al. [13] time–frequency reassignment to improve our bandwidth- propose a method for preserving the temporal envelope of enhanced additive sound model. The bandwidth-enhanced short-duration complex acoustic signals using a homoge- additive representation is in some way similar to tradi- neous sinusoidal model, but it is inapplicable to sounds of tional sinusoidal models [4]–[6] in that a waveform is longer duration, or sounds having multiple transient events. -

Praktikum Iz Softverskih Alata U Elektronici
PRAKTIKUM IZ SOFTVERSKIH ALATA U ELEKTRONICI 2017/2018 Predrag Pejović 31. decembar 2017 Linkovi na primere: I OS I LATEX 1 I LATEX 2 I LATEX 3 I GNU Octave I gnuplot I Maxima I Python 1 I Python 2 I PyLab I SymPy PRAKTIKUM IZ SOFTVERSKIH ALATA U ELEKTRONICI 2017 Lica (i ostali podaci o predmetu): I Predrag Pejović, [email protected], 102 levo, http://tnt.etf.rs/~peja I Strahinja Janković I sajt: http://tnt.etf.rs/~oe4sae I cilj: savladavanje niza programa koji se koriste za svakodnevne poslove u elektronici (i ne samo elektronici . ) I svi programi koji će biti obrađivani su slobodan softver (free software), legalno možete da ih koristite (i ne samo to) gde hoćete, kako hoćete, za šta hoćete, koliko hoćete, na kom računaru hoćete . I literatura . sve sa www, legalno, besplatno! I zašto svake godine (pomalo) updated slajdovi? Prezentacije predmeta I engleski I srpski, kraća verzija I engleski, prezentacija i animacije I srpski, prezentacija i animacije A šta se tačno radi u predmetu, koji programi? 1. uvod (upravo slušate): organizacija nastave + (FS: tehnička, ekonomska i pravna pitanja, kako to uopšte postoji?) (≈ 1 w) 2. operativni sistem (GNU/Linux, Ubuntu), komandna linija (!), shell scripts, . (≈ 1 w) 3. nastavak OS, snalaženje, neki IDE kao ilustracija i vežba, jedan Python i jedan C program . (≈ 1 w) 4.L ATEX i LATEX 2" (≈ 3 w) 5. XCircuit (≈ 1 w) 6. probni kolokvijum . (= 1 w) 7. prvi kolokvijum . 8. GNU Octave (≈ 1 w) 9. gnuplot (≈ (1 + ) w) 10. wxMaxima (≈ 1 w) 11. drugi kolokvijum . 12. Python, IPython, PyLab, SymPy (≈ 3 w) 13. -

Introduction to Matlab
Introduction to Numerical Libraries Shaohao Chen High performance computing @ Louisiana State University Outline 1. Introduction: why numerical libraries? 2. Fast Fourier transform: FFTw 3. Linear algebra libraries: LAPACK 4. Krylov subspace solver: PETSc 5. GNU scientific libraries: GSL 1. Introduction It is very easy to write bad code! • Loops : branching, dependencies • I/O : resource conflicts, • Memory : long fetch-time • Portability : code and data portable? • Readability : Can you still understand it? A solution: look for existing libraries! Why numerical libraries? • Many functions or subroutines you need may have already been coded by others. Just use them. • Not necessary to code every line by yourself. • Check available libs before starting to write your program. • Save your time and efforts! Advantages of using numerical libraries: • Computing optimizations • Portability • Easy to debug • Easy to read What you will learn in this training • General knowledge of numerical libs. • How to check available libs on HPC systems and the web. • How to use numerical libs on HPC systems. • Basic programming with numerical libs. List of notable numerical libraries • Linear Algebra Package (LAPACK): computes matrix and vector operations. [Fortran] • Fastest Fourier Transform in the West (FFTW): computes Fourier and related transforms. [C/C++] • GNU Scientific Library (GSL): provides a wide range of mathematical routines. [C/C++] • Portable, Extensible Toolkit for Scientific Computation (PETSc): a suite of data structures and routines for the scalable (parallel) solution of scientific applications modeled by partial differential equations. [C/C++] • NumPy: adds support for the manipulation of large, multi-dimensional arrays and matrices; also includes a large collection of high-level mathematical functions. -

Fastest Fourier Transform in the West
Fastest Fourier Transform in the West Devendra Ghate and Nachi Gupta [email protected], [email protected] Oxford University Computing Laboratory MT 2006 Internal Seminar – p. 1/33 Cooley-Tukey Algorithm for FFT N 1 2πi − nk Xk = X xne− N ; k = 0; : : : ; N − 1 n=0 2 If we solve for Xk directly then O(N ) operations required for the solution. If N = p × q, then this transformation can be split into two separate transformations... ...recursively, we get the FFT algorithm. N If N is split into r intervals of r each then the complexity is r × N × logr N. This can be generalised to mixed-radix algorithms. MT 2006 Internal Seminar – p. 2/33 Overview of FFT algorithms Cooley-Tukey FFT algorithm (popularized in 1965), known by Gauss in 1805. Prime-factor FFT algorithm ± a.k.a. Good-Thomas (1958-1963), N = N1N2 becomes 2D N1 by N2 DFT for only relatively prime N1; N2. Bruun's FFT algorithm (1978, generalized to arbitrary even composite sizes by H. Murakami in 1996), recursive polynomial factorization approach. Rader's FFT algorithm (1968), for prime size by expressing DFT as a convolution. Bluestein's FFT algorithm (1968) ± a.k.a. chirp z-transform algorithm (1969), for prime sizes by expressing DFT as a convolution. Rader-Brenner (1976) ± Cooley-Tukey like, but purely imag twiddle factors MT 2006 Internal Seminar – p. 3/33 What is FFTW? FFTW is a package for computing a one or multidimensional complex discrete Fourier transform (DFT) of arbitrary size. At the heart of FFTW lies a philosophy geared towards speed, portability, and elegance – achieved via an adaptive software architecture. -
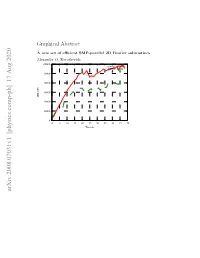
A New Set of Efficient SMP-Parallel 2D Fourier Subroutines
Graphical Abstract A new set of efficient SMP-parallel 2D Fourier subroutines Alexander O. Korotkevich 60000 new lib FFTW 50000 40000 30000 MFLOPs 20000 10000 0 0 5 10 15 20 25 30 35 40 45 50 Threads arXiv:2008.07031v1 [physics.comp-ph] 17 Aug 2020 Highlights A new set of efficient SMP-parallel 2D Fourier subroutines Alexander O. Korotkevich • New set of efficient SMP-parallel DFTs • Free software license • Significant performance boost for large sizes of arrays. A new set of efficient SMP-parallel 2D Fourier subroutines Alexander O. Korotkevicha,b aDepartment of Mathematics & Statistics, The University of New Mexico, MSC01 1115, 1 University of New Mexico, Albuquerque, New Mexico, 87131-0001, USA bL. D. Landau Institute for Theoretical Physics, 2 Kosygin Str., Moscow, 119334, Russian Federation Abstract Extensive set of tests on different platforms indicated that there is a per- formance drop of current standard de facto software library for the Dis- crete Fourier Transform (DFT) in case of large 2D array sizes (larger than 16384 × 16384). Parallel performance for Symmetric Multi Processor (SMP) systems was seriously affected. The remedy for this problem was proposed and implemented as a software library for 2D out of place complex to complex DFTs. Proposed library was thoroughly tested on different available architec- tures and hardware configurations and demonstrated significant (38 − 94%) performance boost on vast majority of them. The new library together with the testing suite and results of all tests is published as a project on GitHub.com platform under free software license (GNU GPL v3). Com- prehensive description of programming interface as well as provided testing programs is given. -

2019 Julia User & Developer Survey
User & Developer Survey 2019 Viral B. Shah Andrew Claster Abhijith Chandraprabhu Methodology We conducted 1,834 interviews online among Julia users and developers June 12-24, 2019 Margin of error is +/- 2.3 percentage points We recruited respondents online using Slack, Discourse, Twitter, email, JuliaLang.org and JuliaComputing.com The survey was administered only in English, but more than half of respondents come from non-English speaking countries 2 56% of Respondents Use Julia a ‘Great Deal’ While 38% Use Julia ‘Some’ Python and Bash/Shell/PowerShell are 2nd and 3rd among Julia Users and Developers How frequently do you use each of the following languages? Great deal Some Julia 56% 38% 94% Python 39% 42% 81% Bash/Shell/PowerShell 23% 46% 69% MATLAB 16% 27% 43% C++ 11% 29% 40% C 8% 32% 40% R 15% 23% 38% SQL 11% 23% 34% JavaScript 6% 21% 27% Java 5% 13% 18% C# 2% 6% 8% Scala 1%5 % 6% 3 93% of Respondents Like Julia or Say Julia Is One of Their Favorite Languages Python Comes Second Among Julia Users and Developers How much do you like each of the following languages? One of my favorite languages Like Julia 73% 20% 93% Python 26% 35% 61% C 6% 21% 27% R 9% 14% 23% Matlab 8% 15% 23% C++ 6% 17% 23% Bash/Shell/PowerShell 4% 18% 22% SQL 3% 13% 16% JavaScript 2% 9% 11% Java 2% 8% 10% C# 2% 7% 9% Scala 2% 5% 7% 4 The MOST Popular TECHNICAL Features of Julia Are Speed/Performance, Ease of Use, Open Source, Multiple Dispatch and Solving the Two Language Problem Thinking only about the TECHNICAL aspects or features of Julia, what are the TECHNICAL -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae